裂面形貌扰动对晶内微裂纹演变影响的有限元分析

王远鹏，黄佩珍

(南京航空航天大学 航空宇航学院，江苏 南京，210016)

摘  要：根据表面扩散控制下物质迁移规律，建立有限单元法，对裂面形貌扰动下二维微裂纹演变过程进行数值模拟。结果表明：裂尖的几何形状对微裂纹圆柱化时间起决定性作用；在裂面形貌扰动振幅不变的情况下，扰动频率越高，其对裂腔分节临界形态比的影响越小，且波数为奇数的微裂纹更容易分节；振幅对裂腔分节起阻碍作用；裂面形貌扰动频率越小，振幅对裂腔分节临界形态比的影响越显著。

关键词：晶内微裂纹；表面扩散；有限单元法；裂面形貌扰动；形貌演变

中图分类号：TG113.2        文献标识码：A         文章编号：1672-7207(2008)04-0760-05

Finite element analysis of shape evolutions for intragranular microcracks with surface perturbation

WANG Yuan-peng, HUANG Pei-zhen

(College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China)

Abstract: Based on the theory of surface diffusion, a finite element method was developed to simulate shape evolutions of two-dimensional microcracks with surface perturbation. The results show that the cylinderization time depends sensitively on the initial morphology of the microcrack tip. When the amplitude of the perturbation is given, the frequency effect on the critical aspect ratio is weakened with the increase of perturbation. The microcrack is easy to split into two parts when the number is uneven, while the splitting process is interfered with by the amplitude. When the frequency is small, the amplitude has an obvious effect on the critical aspect ratio.

Key words: intragranular microcracks; surface diffusion; finite element method; surface perturbation; shape evolutions

近年来，金属材料内部损伤微裂纹的扩散愈合过程逐步成为材料学和力学界的关注热点^[1-9]，研究方法包括实验观察和数值模拟。以金属材料为主体的实验研究直观形象，便于深化对金属材料内部表面和界面扩散作用与机理的理解。张海龙等^[1-3]对真空退火条件下金属内部疲劳微裂纹的扩散愈合过程进行了SEM观察。以物理系统的微观描述为出发点的分子动力学模拟日趋成熟，可较真实地反映材料的微观动力学过程；以有限元理论为基础的数值模拟灵活高效，便于定量化揭示各种参数对愈合过程的影响。Wei等^[4]采用分子动力学方法在纳观尺度上模拟了BCC-Fe中内部裂纹的愈合过程。张永军^[5]对面心立方晶格Cu单晶中心贯穿裂纹愈合过程的形态演化进行了分子动力学模拟。Huang等^[6-7]采用建立在质流基础上的描述微结构演化的有限单元法对表面扩散、界面迁移、表面扩散和晶界扩散控制下微米级微裂纹的形态演变过程进行了数值分析，实验和数值模拟结果表明，无论损伤微裂纹初始位于晶内、晶界或穿晶等不同位置，均可在不同或耦合的扩散机制下通过其形态演变和体积收缩等阶段被最后愈合。

自从1878年Rayleigh^[10]发现液柱的断节分解现象以来，人们对物体表面形貌扰动的认识逐渐深入。Huynh等^[11]分析了两列波叠加对液柱的扰动作用；Nichols和 Mullins^[12]将Rayleigh的扰动分析推广到固体圆柱表面；Ma^[13]研究了正弦形貌扰动作用下棒状物的演变，结果表明表面形貌对微结构演变的影响非常大。然而，这些研究都是针对实体表面的，而对物体中微孔洞、微裂纹的表面形貌扰动的研究很少。材料中实际的微裂纹形状并不规则，裂腔表面粗糙起伏，很难用数学表达式精确描述。在以往的文献研究中，一般都将微裂纹简化为理想模型：光滑椭圆或规则板状的二维裂纹、光滑币型三维裂纹。因此，有必要将形貌扰动分析从实体推广到空穴。在此，本文作者应用表面扩散控制下微结构演变的有限元方法^[14]，分析裂面形貌扰动对微裂纹演变过程的影响。

1  基本理论

1.1  基本公式

根据Herring的经典理论^[15]，表面原子迁移的动力学可描述为：

设v_ns为表面法向速度，δr_ns为表面法向虚位移，则物质守恒定律要求

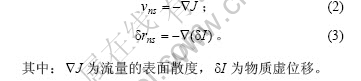
1.2  包含蒸发-凝结机制的弱解描述

由于单纯的表面扩散机制难以用有限元法实现，故在模拟材料微结构演变中需引入蒸发-凝结机制。对于并非远离平衡状态的蒸发-凝结过程，其晶粒表面每一点动力学定律为

当表面扩散和蒸发-凝结机制同时作用时，表面法向速度和表面法向虚位移分别为

设_δG为表面能增量，根据广义虚位移原理，有

将动力学定律(1)和(4)代入式(6)，并利用式(5)消去v_nv和δr_ns，可得

1.3  有限元方法

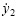假设微裂纹第三维尺寸较大，可简化为二维问题，故可用线性单元来近似描述其形状。图1所示为1个典型的线性单元，2个节点坐标为(x₁, y₁)和(x₂, y₂)，单元长度为l、倾角为θ。每个单元须有4个自由度(δx₁, δy₁, δx₂, δy₂)来描述单元的运动，3个自由度(δI₁, δI₂, δI_m)来描述表面扩散，其中δI₁，δI₂和δI_m为单元两节点和中点的虚物质位移。设，，和为节点速度，J₁，J₂和J_m为单元两节点及中点的物质流量，则在总体坐标系中，用δq^e表示单元的广义虚位移，表示广义速度：

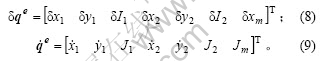
在长度为l的单元中，任一离中点距离为s处存在如下关系：

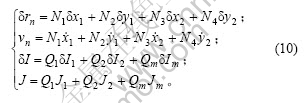
其中，插值函数为

当节点1和2分别有位移(δx₁, δy₁)和(δx₂, δy₂)时，单元长度变化为

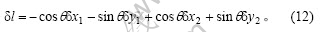
相应单元的表面能增量为

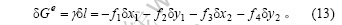
其中：f_i(i=1, 4)是由单元伸长产生的作用于两节点上的节点力。

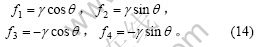
对式(7)曲线积分，可得有限单元方程

由于物质表面能只取决于物体形状，故δI₁，δI₂和δI_m不产生节点力，因此，

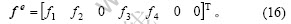
单元粘度矩阵为

无量纲参数mL²/M(其中L为最大单元长度)可度量蒸发-凝结与表面扩散2种竞争机制的相对强弱。由于这里只考虑物质扩散，根据动力学定律和物质守恒定律可知，当  mL²/M ＜＜1时，由蒸发-凝结机制引起的物质泄漏可忽略。文中全部采用mL²/M=10^-6，因而，裂纹在演变过程中裂腔横截面面积保持不变。

图 1  线性单元

Fig.1  Linear element

2  数值计算与讨论

基于所建立的有限元方程并编制相应程序，分析表面扩散控制下裂面形貌扰动对二维微裂纹演变规律的影响。计算过程中裂腔横截面的总面积几乎保持不变，符合物质守恒定律，表明本文的计算精度是可靠的。由裂面对称性，取1/4裂纹截面进行研究，并采用形态比β=D₀/h₀来描述椭圆形微裂纹，无量纲化时间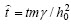(其中：h₀为裂腔短轴长度；D₀为裂腔长轴长度)。为研究裂面形貌扰动的影响，本文采用在椭圆周上叠加正弦波形的方法来模拟真实裂面，如图2所示。为分析方便，令正弦波的波长和振幅分别为λ和a，并假设裂腔长轴与扰动波长之比k=D₀/λ，无量纲化振幅c=2a/h₀。考虑到计算中边界条件的处理和裂面形貌扰动规律便于分析，令k为整数。

图2  裂面形貌扰动示意图

Fig.2  Schematic diagram of microcrack with surface perturbation

2.1  裂面形貌扰动对裂腔圆柱化时间的影响

对于裂面光滑的微裂纹，文献[4]表明，当形态比   β＜133时，微裂纹将直接圆柱化。本文采用初始形态比β=50并具有光滑裂面的微裂纹为基准，首先计算其圆柱化时间，作为基准时间。然后，计算具有相同初始形态比β但受裂面形貌扰动影响的微裂纹圆柱化时间，并与基准时间进行比较，从而定量化揭示形貌扰动对裂腔圆柱化时间的影响规律。

2.1.1  波长的影响

为了定量化揭示形貌扰动波长对裂腔圆柱化时间的影响，对一系列具有不同k的微裂纹演变过程进行数值模拟，得到如图3所示微裂纹圆柱化时间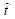随k变化的曲线，其中固定振幅c=0.1。经过多次计算，发现k的奇偶性对微裂纹的演变过程产生重要影响，因此，有必要分组讨论。图中虚线表示光滑裂面情况下，微裂纹圆柱化所需时间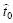<0.74。由图3可知，随着k增加，裂面形貌扰动对裂面各点化学位的影响不断削弱，k为奇数和偶数2种情况下的圆柱化时间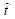随着k的增加都逐渐趋近于0.74，且在k＜12时，k的影响非常显著。由于k为奇数时，有形貌扰动的微裂纹裂尖曲率小于无形貌扰动时微裂纹的尖曲率，其裂尖的化学位差(绝对值)小于后者，所以相应的圆柱化时间要长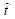，＞0.74，且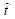随k增加而减小。当k为偶数时，情况恰好与之相反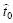，＜0.74，且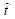随k增加而增大。由此可见，裂尖的几何形状对微裂纹圆柱化时间起着决定性作用。

1―k为奇数；2―k为偶数；3―光滑表面

图3  微裂纹圆柱化时间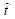随k变化曲线

Fig.3  Relationship between cylinderization time and k

2.1.2  振幅的影响

固定k，改变无量纲化振幅c，可以得到如图4所示微裂纹圆柱化时间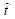随c变化曲线。虚线表示裂面光滑情况下，微裂纹圆柱化所需时间。由图4可知，k为1，3和5时的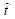―c曲线在虚线以上；虚线以下曲线对应的k为2，4和6。当k为偶数时，微裂纹裂尖随振幅增大而变尖，化学位差相应增加，裂尖附近的原子往裂尖扩散的驱动力增大，所以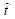，随之减小。反之，当k为奇数时，由于微裂纹的裂尖曲率随振幅增大而变小，原子向裂尖扩散的驱动力减小，故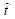增大；且当k较大时，其与c呈近似线性关系。此外，随着k增大，形貌扰动的作用不断减弱，因此，裂面圆柱化时间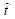受振幅c的影响随之减弱。

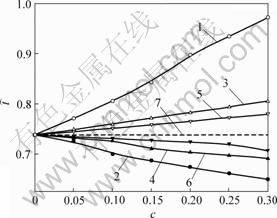
1―k=1; 2―k=2; 3―k=3; 4―k=4; 5―k=5;

6―k=6; 7―光滑表面

图4  微裂纹圆柱化时间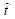随c变化曲线

Fig.4  Relationship between cylinderization time and c

2.2  裂面形貌扰动对裂腔分节临界点的影响

对于裂面光滑的微裂纹，文献[4]表明：当形态比β≥133时，微裂纹中心上下裂面所形成的凸起不断长大并相接，导致微裂纹裂腔分成2部分。此时，裂腔分节临界形态比β_I=133。本文在分析过程中，同样采取改变正弦波形的波长和振幅，得出相应的临界形态比β，然后，与β_I进行比较、分析。

2.2.1  波长的影响

固定c=0.1，改变k，计算出每个k所对应的临界形态比β，可以得到如图5所示β-k关系曲线。由图5可知，在椭圆形微裂纹裂面叠加的正弦波形越稠密(即裂面形貌扰动越严重)，裂腔分节β越小；当k＜30且为偶数时，相应的β明显大于k为奇数时的β；当k＞30时，可忽略k对β的影响。也就是说，在裂面形貌扰动振幅不变的情况下，扰动频率越高，其对β的影响越小；扰动波数为奇数时，微裂纹更容易分节。

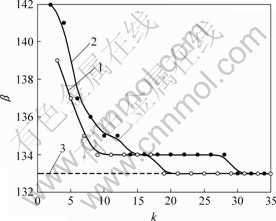
1―k为奇数；2―k为偶数；3―光滑表面

图5  临界形态比β随k变化曲线

Fig.5  Relationship between critical aspect ratio β and k

2.2.2  振幅的影响

对于某一固定k，改变c，计算出相应的临界形态比β，可以得到如图6所示的β-c关系曲线。由图6可知，无论k为奇数或偶数，β都随振幅c的增大而增加，且与c呈近似线性关系；从各条曲线的斜率上看，当k为偶数(即裂尖曲率较大)时，β更易受振幅c的影响；k越小，即裂面形貌扰动频率越小，β受c的影响越显著。

1―k=2; 2―k=3; 3―k=4; 4―k=5; 5―k=6; 6―k=7

图6  临界形态比β随c变化曲线

Fig.6  Relationship between critical aspect ratio β and c

3  结  论

a. 裂尖的几何形状对微裂纹圆柱化时间起决定性作用。当裂纹直径与扰动波长比k为奇数时，形貌扰动使微裂纹圆柱化时间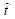延长，且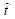随k的增加而减小；当k为偶数时，形貌扰动使微裂纹圆柱化时间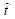缩短，且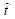随k的增加而增加。

b. 当k为奇数时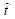，随振幅c的增加而增加；当k为偶数时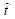，随c的增加而近线性减小。随着扰动频率的增大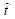，受振幅c的影响逐渐减弱。

c. 在振幅c不变的情况下，裂纹直径与扰动波长比k越大，裂面形貌扰动对裂腔分节临界形态比β_临界的影响越小，且k为奇数时，微裂纹更容易分节。

d. β_临界随振幅c的增大而增加，即振幅对裂腔分节起阻碍作用；k越小，β_临界受振幅c的影响越显著；k为偶数时，振幅对裂腔分节的阻碍作用更明显。

参考文献：

[1] 张海龙, 孙 军. 工业纯铁内部疲劳微裂纹扩散愈合过程中的形态演变[J]. 金属学报, 2002, 38(3): 239-244.
ZHANG Hai-long, SUN Jun. Morphological evolution of internal fatigue microcracks in alpha-iron during diffusive heating[J]. Acta Metallurgica Sinica, 2002, 38(3): 239-244.

[2] ZHANG Hai-long, HUANG Pei-zhen, SUN Jun, et al. Morphological healing evolution of penny-shaped fatigue microcracks in pure iron at elevated temperatures[J]. Applied Physics Letters, 2004, 85(7): 1143-1145.

[3] 杨君刚, 张海龙, 孙 军. 工业纯镁内部疲劳微裂纹的热扩散性愈合[J]. 金属学报, 2005, 41(8): 819-823.
YANG Jun-gang, ZHANG Hai-long, SUN Jun. Diffusive healing of internal fatigue microcracks in pure magnesium[J]. Acta Metallurgica Sinica, 2005, 41(8): 819-823.

[4] Wei D B, Han J T, Tieu A K, et al. Simulation of crack healing in BCCFe[J]. Scripta Materialia, 2004, 51(6): 583-587.

[5] 张永军. 金属材料内裂纹愈合过程的物理模拟与计算机模拟[D]. 北京: 北京科技大学材料科学与工程学院, 2003.
ZHANG Yong-jun. Physical and numerical simulation of inner crack healing in metals[D]. Beijing: School of Materials Science and Engineering, University of Science and Technology Beijing, 2003.

[6] HUANG Pei-zhen, SUN Jun. A numerical analysis of intergranular penny-shaped microcrack shrinkage controlled by coupled surface and interface diffusion[J]. Metall Mater Trans A, 2004, 35(4): 1301-1309.

[7] HUANG Pei-zhen, SUN Jun, LI Zhong-hua. Evolution of penny-shaped microcracks by interface migration[J]. Inter J Solid Struc, 2003, 40(8): 1959-1972.

[8] WANG Hua, LI Zhong-hua. The three-dimensional analysis for diffusive shrinkage of a grain-boundary void in stressed solid[J]. J Mater Sci, 2004, 39(10): 3425-3432.

[9] WANG Hua, LI Zhong-hua, SUN Jun. Effects of stress and temperature gradients on the evolution of void in metal interconnects driven by electric current and mechanical stress[J]. Model Simul Mater Sci, 2006, 14(4): 607-615.

[10] Rayleigh L. On the instability of jets[J]. Proc London Math Soc, 1879, 10(4): 361-371.

[11] Huynh H, Ashgriz N, Mashayek F. Instability of a liquid jet subject to disturbances composed of two wavenumbers[J]. Fluid Mech, 1996, 320: 185-210.

[12] Nichols F A, Mullins W W. Morphological changes of surface of revolution due to capillarity-induced surface diffusion[J]. J Appl Phys, 1965, 36: 1826-1835.

[13] MA Qian. A model for the breakup of rod morphologies[J]. Scripta Materialia, 1997, 36(1): 77-82.

[14] SUN Bing, SUO Zhi-gang. A finite element method for simulating interface motion (Ⅱ): Large shape change due to surface diffusion[J]. Acta Mater, 1997, 45(12): 4953-4962.

[15] Herring C. The physics of powder metallurgy[M]. New York: McGraw-Hill, 1951.

收稿日期：2007-06-04；修回日期：2007-10-26

基金项目：国家自然科学基金资助项目(10702028)；南京航空航天大学引进人才科研基金资助项目(S0372-013)

通信作者：黄佩珍(1972-)，女，浙江浦江人，博士，教授，从事材料微结构演变和计算力学等研究；电话：13770835075；E-mail: pzhuang@nuaa.edu.cn