基于SVM和混沌PSO的除钴过程工艺指标预测
朱红求1，阳春华1，桂卫华1，李勇刚1，钱坚2
(1. 中南大学 信息科学与工程学院，湖南 长沙，410083；
2. 宜春钽铌矿，江西 宜春，336003)
摘 要：针对锌湿法冶炼除钴过程存在非线性和大时滞的特点，提出一种基于支持向量机和混沌粒子群算法的工艺指标(钴离子浓度)预测方法。为提高粒子群算法的搜索性能，提出一种基于非优胜粒子混沌变异和全局最优值小范围扰动的混沌变异粒子群算法。采用混沌粒子群算法优化模型参数，采用二进制粒子群算法选择输入属性，以减少模型的复杂度，提高模型的预测精度。研究结果表明：所提出的模型精度满足当溶液杂质离子质量浓度在小于1 mg/L时绝对误差小于0.1 mg/L的现场工艺标准。
关键词：除钴过程；工艺指标预测；支持向量机；混沌PSO
中图分类号：TP273 文献标志码：A 文章编号：1672-7207(2010)04-1424-05
Prediction of technical index for cobalt removal process based on SVM and chaotic PSO
ZHU Hong-qiu1, YANG Chun-hua1, GUI Wei-hua1, LI Yong-gang1, QIAN Jian2
(1. School of Information Science & Engineering, Central South University, Changsha 410083, China;
2. Yichun Tantalum & Niobium Mine, Yichun 336003, China)
Abstract: Considering the characteristics of strong non-linearity and large time delay in cobalt removal process of zinc hydrometallurgy, a prediction method of technical index (cobalt concentration) combining the least square support vector machine (LS-SVM) and chaotic particle swarm optimization (CPSO) was proposed. CPSO used the mutation of the non-winner particles by chaotic search and mutation of the global best position by using small extent of disturbance to improve its search performance. The model parameters were optimized by CPSO and the input attributes were selected by binary PSO, which reduces the complexity and improves the prediction accuracy. The results show that prediction accuracy of the proposed model meets the technology requirements that the absolute error will be less than 0.1 mg/L when the solution concentration is less than 1 mg/L.
Key words: cobalt removal purification process; prediction of technical index; LS-SVM; chaotic PSO
净化过程是锌湿法冶炼生产中最为重要的一个工序[1-2]，是电解过程优质、高效生产的重要前提。净化除钴是三段逆锑盐净化过程中最关键的一步，溶液从流进到流出需要约2 h，过程流程长，滞后时间长，过程操作优化困难。目前，一般通过添加过量锌粉来保证溶液杂质离子浓度满足工艺要求，特别是当出口浓度超过工艺标准时，则停止溶液循环，并在净化槽内补加大量的锌粉，直到溶液合格后再开车循环，这样，造成大量的锌粉浪费和能源消耗。对于净化除钴过程，其关键工艺指标是出口溶液钴离子浓度，它是净化除钴过程优化控制的目标。出口溶液钴离子质量浓度是除钴过程的关键工艺指标，其准确的预测是优化控制的基础[3-5]。为此，本文作者结合过程机理研究和数据分析，提出一种基于最小二乘支持向量机(LS-SVM)的工艺指标预测方法，采用粒子群算法(PSO)对模型进行输入属性选择以及模型参数优化，以净化过程生产数据进行实验验证分析。
1 净化过程分析
在锌湿法冶炼过程中，钴是危害电解过程的主要杂质，也是难以去除的杂质之一[6-7]，因此，在三段净化过程中，Ⅱ段净化除钴是净化过程的关键。该工序如图1所示，主要包括4个反应槽(4~7号)，溶液经过加热后从4号槽进入，锑盐和锌粉在4号槽加入，依次通过5~7号槽后，通过压滤后进入净化除镉。在一定的流量下，溶液流经每个槽需要约30 min，总时间约2 h，是一类典型的长流程复杂工业生产过程。正是由于这种大滞后，使得净化过程优化控制困难，过程参数设定凭个人经验操作，主观性和盲目性大，锌粉消耗大。
净化除钴主要是通过在溶液中添加锌粉和锑盐，置换除去溶液中的杂质Co2+[8]，其中锑盐作为活化剂。其化学反应方程为：
Co2++SbO2+4H++Zn+3e=CoSb+Zn2++2H2O (1)
=
(2)
从上述反应方程式可以看出：硫酸锌溶液中加锌粉锑盐除钴过程复杂，并非简单金属置换反应，存在复杂的非线性关系。
通过偏相关分析，最终确定影响净化过程出口浓度的因素主要包括入口溶液的镉钴离子质量浓度、流量、温度和锌粉添加量等因素。支持向量机采用核函数思想将非线性问题转为线性问题来解决，具有全局最优以及较强泛化能力等优点[9-10]，因此，采用支持向量机预测净化过程的出口溶液钴离子质量浓度，以期实现净化过程锌粉添加量的优化控制。
2 基于模糊支持向量机的预测模型
在支持向量机回归法中，对于给定的训练样本集S=(xi, yi), (i=1, 2, 3, … , N) (其中：m维输入
，一维输出
)。利用非线性映射函数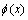
可将样本非线性地映射到高维特征空间，将原样本空间中的非线性函数估计问题转化成高维特征空间中线性函数估计问题[11]：
(3)
式中：w为权向量；b为偏差。这一回归问题可根据结构风险最小化原理表示为一个等式约束的优化 问题：
s.t. 
(4)
式中：C为惩罚系数；ei为误差。
为求解上述优化问题，建立拉格朗日等式，把约束优化问题变为无约束优化问题：
(5)
式中：
为拉格朗日乘子。
图1 Ⅱ段净化过程工艺流程简图
Fig.1 Flow diagram of second stage in purification process
根据Karush-Kuhn-Tucker（KTT）条件得到：
(6)
再根据Mercer条件定义，有
(7)
从方程组(6)中消去ei和w后，可以得到：
(8)
由式(8)可知：最小二乘支持向量机的训练问题可归结为一个线性方程组的求解问题，而不是求解一个二次型规划问题，从而使得其计算简单、快速。
采用最小二乘法求得公式(8)的系数
和b，并代入(3)式，得到支持向量机的输出：
(9)
核函数选用径向基函数：
(10)
式中：
为径向基函数的宽度。
选取Ⅱ段入口溶液钴离子浓度(x1)、Ⅱ段入口溶液温度(x2)和流量(x3)、锌粉添加频率(x4)、锑盐流量(x5)和Ⅱ段入口溶液的镉离子质量浓度(x6)等因素作为输入变量，对应时刻Ⅱ段后液钴离子浓度作为输出。将上述变量组成的自变量矩阵代入式(4)中的约束项，采用最小二乘支持向量机，则压滤后滤液中钴离子质量浓度预测模型表示为：
(11)
式中：cBCo, T, Q, f, cFCo, cFCd和QFsb分别表示压滤后液钴离子浓度、入口溶液的温度和流量、锌粉添加频率、入口钴、镉离子质量浓度以及锑盐流量；l，m，n，p，q，τ和j分别表示输入变量相应的阶数。
3 输入属性选择及模型参数优化
在支持向量机预测模型中，输入属性的选择对于提高预测的精度以及计算性能非常重要，在输入属性过多时尤为重要。此外，模型参数C和核函数中的选择对于预测精度影响大[12-13]。如何合理选择输入属性以及SVM 的参数成为支持向量机模型的一个重要问题。对于这些参数的优化，一般通过遗传算法或网格法求解，但这些方法计算耗时大且易陷入局部极小值。本文作者采用粒子群算法来优化SVM 的输入选择与模型参数，对于模型属性选择，采用离散的二进制离子群算法[14-15]，而对于模型参数的优化则采用混沌离子群算法。
在标准粒子群算法后期，若粒子群的最优个体位置以及全局最优位置变化很小，则其速度更新将主要由
来决定。而权值往往小于1，因此，速度越来越小，这就意味着粒子群易于陷入局部最优而出现早熟收敛现象。为了克服这一缺陷，采用混沌搜索变 异[16-17]等方法，对非优胜粒子以及全局最优位置进行混沌扰动，协助粒子群跳出局部最优位置。定义最优适应值变化率k为：
(12)
式中：f(t)为种群第t代的最优适应值；
为种群第(
)代的最优适应值；k为种群在最近进化T代内最优适应值的相对变化率。当k小于某一设定阈值时，可以认为粒子群算法进入了一个局部最优点，从而启动混沌变异算法，对粒子群中的优胜粒子进行速度和位置的更新，而非优胜粒子则映射为混沌变量，进行混沌优化后，与更新后的优胜粒子组成新的种群。将适应值较高的优胜个体按照标准离子群算法进行速度和位置的更新，得到子种群Popul 1；种群中适应值较低的非优胜个体x(k)按照下式映射为混沌变量：
(13)
式中：xmax 和xmin分别表示x(k)位置向量的上界和下界。将得到的混沌变量按照式(14)进行变异后得到x(k+1)，并根据式(15)映射为位置向量：
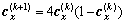(14)
(15)
这样，就得到变异后的子种群Popul 2。将Popul 1和Popul 2组成新的种群。
同时，对当前的全局最优值也采用混沌搜索方法进行小范围的扰动，通过混沌优化操作使种群跳出局部最优点，增大寻找全局最优解的概率。将全局最优值gbest映射到区间[0，1]后形成变量ξ，则全局最优值的混沌变异按照下式进行：
(16)
式中：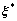
为混沌变异后的位置向量；
为按照式(14)迭代k次后的混沌变量；a为缩放因子。此外，在种群初始化时，采用混沌变量对粒子的位置和速度进行初始化，这样可以在保证初始变量随机性的前提下，提高种群的多样性和遍历性。
4 实验仿真与分析
为了验证所提出的预测模型的有效性，采用历史数据进行训练和采用连续生产数据进行验证。采用基本二进制粒子群算法和混沌粒子群算法同时对输入属性和模型参数分别进行优化，属性初始阶数设为3。在属性选择中，采用二进制编码方案对属性进行编码，用长度为D的二进制串来表示1个粒子，该串上的每一位对应待选择的一个属性，取1时则表示选择该属性，取0时则表示不选择该属性，最大迭代次数设定为1 000次，种群数设为30。混沌离子群算法的种群数设为50，惯性因子在0.9~0.4之间采用线性下降的方法，学习因子c1和c2的取值设为2.0，最大迭代次数设定为500次，收敛判断标准为k≤0.001。采用现场调研收集的近2月的生产数据作为训练样本数据，去除生产不正常状态以及生产系统检修时的数据，共获得800组数据，其中600组数据用来训练，200组数据作为粒子群算法优化的校验数 据，以校验数据集的预测结果与实际值的平均绝对百分误差(EMAP)作为适应度函数，通过寻找一组最优的参数向量，使得测试样本集的预测值与实际值的EMAP最小。
经过模型训练后，输入属性选择入口溶液的钴离子浓度、入口溶液的温度和流量、锌粉添加频率和入口溶液的镉离子质量浓度，阶数分别为1。然后，采用现场连续运行1周共168组数据对所得到的模型进行验证，并与标准最小二乘支持向量机进行对比。图2和图3所示分别为采用LS-SVM和SVM+PSO方法的仿真计算结果。
图2 LS-SVM仿真结果
Fig.2 Simulation results of LS-SVM
图3 SVM+PSO仿真结果
Fig.3 Simulation results of SVM+PSO
从图2和3可以看出：在生产数据波动较大时，支持向量机建模方法仍然能够取得比较好的效果；采用SVM+PSO方法，66.07%的样本误差小于5%，仅有5个样本误差大于10%；而采用LS-SVM方法，误差在5%以下的样本仅为55.95%，有28个样本误差大于10%，采用SVM+PSO方法的预测精度明显高于LS-SVM方法的预测精度。可见，通过粒子群算法选择输入属性以及模型参数优化，最小二乘支持向量机的泛化能力提高。同时，在SVM+PSO方法中，最大绝对误差为0.079 8 mg/L，满足当溶液质量浓度在 1 mg/L以下时绝对误差小于0.1 mg/L的现场工艺标准，可以用于净化除钴过程的优化控制。
5 结论
(1) 提出了一种基于最小二乘支持向量机和粒子群算法的除钴过程工艺指标预测方法，实现了出口溶液钴离子质量浓度的准确预测。
(2) 提出了基于二进制粒子群算法和混沌粒子群算法的模型输入属性选择和参数优化方法，减少了模型的冗余属性信息，提高了模型的预测精度。
(3) 模型泛化能力强，精度高，预测精度满足现场工艺要求标准，可以指导现场进行优化控制。
参考文献：
[1] Boyan S B, Victoria V K, Nikolai K K. Purification of zinc sulfate solutions from cobalt and nickel through activated cementation[J]. Hydrometallurgy, 2004, 73(2): 163-168.
[2] Raghavan R, Mohanan P K, Verma S K. Modified zinc sulphate solution purification technique to obtain low levels of cobalt for the zinc electrowinning process[J]. Hydrometallurgy, 1999, 51(2): 187-206.
[3] 侯志祥, 吴义虎, 袁松贵, 等. 基于AEPSO优化的神经网络多步预测控制[J]. 中南大学学报: 自然科学版, 2007, 38(6): 1162-1168.
HOU Zhi-xiang, WU Yi-hu, YUAN Song-gui, et al. Multi-steps predictive control of neural networks based on AEPSO optimization[J]. Journal of Central South University: Science and Technology, 2007, 38(6): 1162-1168.
[4] Peng H, Wu J, Garba I, et al. Nonlinear system modeling and predictive control using the RBF nets-based quasi-linear ARX model[J]. Control Engineering Practice, 2009, 17(1): 59-66.
[5] Paolo L, Bruno M, Claudio A. Modeling and predictive control of a new injection system for compressed natural gas engines[J]. Control Engineering Practice, 2008, 16(10): 1216-1230.
[6] Yang D J, Xie G, Zeng G S, et al. Mechanism of cobalt removal from zinc sulfate solutions in the presence of cadmium[J]. Hydrometallurgy, 2006, 81(1): 62-66.
[7] Zeng G S, Xie G, Yang D J, et al. The effect of cadmium ion on cobalt removal from zinc sulfate solution[J]. Minerals Engineering, 2006, 19(2): 197-200.
[8] 郭忠诚, 阎江峰, 杨显万. Sb2O3在硫酸锌溶液净化除钴过程中的机理[J]. 中国有色金属学报, 2000, 10(5): 697-700.
GUO Zhong-cheng, YAN Jiang-feng, YANG Xian-wan. Mechanism of Sb2O3 in removal of cobalt in zinc sulphate solution[J]. The Chinese Journal of Nonferrous Metals, 2000, 10(5): 697-700.
[9] Vapnik V N. An overview of statistical learning theory[J]. IEEE Trans on Neural Networks, 1999, 10(5): 988-999.
[10] Esen H, Inalli M, Sengur A, et al. Modeling a ground-coupled heat pump system by a support vector machine[J]. Renewable Energy, 2008, 33(8): 1814-1823.
[11] Suykens J A K, Vandewalle J. Least squares support vector machine classifiers[J]. Neural Processing Letters, 1999, 9(3): 293-300.
[12] Wu C H, Tzeng G H, Lin R H. A Novel hybrid genetic algorithm for kernel function and parameter optimization in support vector regression[J]. Expert Systems with Applications, 2009, 36(3): 4725-4735.
[13] Fang S F, Wang M P, Qi W H, et al. Hybrid genetic algorithms and support vector regression in forecasting atmospheric corrosion of metallic materials[J]. Computational Materials Science, 2008, 44(2): 647-655.
[14] Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//Proceedings of IEEE International Conference on Systems, Man, and Cybernetics. New York: IEEE, 1997: 4104-4108.
[15] Rapai? M R, Kanovi? ?, Jeli?i? Z D. Discrete particle swarm optimization algorithm for solving optimal sensor deployment problem[J]. Journal of Automatic Control, 2008, 18(1): 9-14.
[16] Coelho L D S, Lee C S. Solving economic load dispatch problems in power systems using chaotic and Gaussian particle swarm optimization approaches[J]. International Journal of Electrical Power & Energy Systems, 2008, 30(5): 297-307.
[17] Meng H J, Zheng P, Wu R Y, et al. A hybrid particle swarm algorithm with embedded chaotic search[C]//Proceedings of the 2004 IEEE Conference on Cybernetics and Intelligent Systems. Singapore: IEEE, 2004: 367-371.
收稿日期：2009-08-11；修回日期：2009-11-17
基金项目：国家自然科学基金资助项目(60874069)；湖南省自然科学基金资助项目(09JJ3122)；国家高技术研究发展计划(“863”计划)资助项目(2009AA04Z124)
通信作者：朱红求(1970-)，男，湖南娄底人，博士，从事复杂工业过程建模与优化研究；电话：0731-88830394；E-mail:hq5114@163.com
(编辑 刘华森)
