Co-A1-O磁性纳米颗粒膜微波磁性研究
舒畅1,邓联文1, 2,杨兵初1,熊健1,左舜贵1,梁丽杰1
(1. 中南大学 物理科学与技术学院,湖南 长沙,410083;
2.中南大学 粉末冶金国家重点实验室,湖南 长沙,410083)
摘要:通过实验研究和理论计算模拟研究Co-A1-O磁性纳米颗粒膜的微波磁性。首先采用双靶反应磁控溅射工艺制备Co-A1-O磁性纳米颗粒膜,探讨工艺条件对薄膜微波磁谱的影响;然后,利用Landau-Lifshitz-Gilbert方程和Bruggeman有效媒质理论,计算模拟主要磁参量变化对磁性纳米颗粒膜磁谱的影响。研究结果表明:增大Co靶溅射功率,可使磁性颗粒间因分布电容效应引起的涡流损耗增加,从而使磁谱的共振线宽增大;阻尼系数增大导致磁导率频谱的共振线宽增大趋势与实验结果基本一致。
关键词:Co-A1-O颗粒膜;磁导率;LLG方程;有效媒质理论
中图分类号:TM271 文献标志码:A 文章编号:1672-7207(2012)02-0472-05
Microwave magnetism of Co-A1-O nano-granular film
SHU Chang1, DENG Lian-wen1, 2, YANG Bing-chu1, XIONG Jian1, ZUO Shun-gui1, LIANG Li-jie1
(1. School of Physics Science and Technology, Central South University, Changsha 410083, China;
2. State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China)
Abstract: To research magnetic characteristics of nano-granular film such as Co-Al-O in the microwave range, related research was studied experimentally and theoretically. Co-Al-O nano-granular films with high microwave permeability were synthesized by magnetron sputtering technology and effect of the major parameters on preparation was discussed. Analytic calculation of effective permeability frequency spectra of the nano-granular thin film was presented based on the Landau-Lifshitz-Gilbert equation and Bruggeman effective medium theory. The results show that the eddy current losses caused by capacitive effect between the particles increase with the increase of the Co sputtering power, and the resonance linewidth broadens. Increased damping parameter will broaden the absorption bandwidth. The simulation results agrees well with the experimental ones.
Key words: Co-A1-O nano-granular film; permeability; LLG equation; effective medium theory
信息技术的飞速发展和电子元器件的微型化趋势对高频磁性材料性能要求越来越高[1-2]。另一方面,电讯技术的发展也引发电磁干扰和电磁污染日趋严重,对能吸收衰减电磁波能量的吸波材料提出了迫切需求。FeCo类磁性纳米颗粒膜在几GHz频段具有较高磁导率,并可以在一定频段具有较高磁损耗,可以应用于高频微磁器件或抗电磁干扰设计中。通过控制颗粒膜中金属含量、颗粒粒度、颗粒间距等结构参量,可以实现对其电磁性能的剪裁调控[3]。磁性纳米颗粒膜的微结构对其磁导率影响较大,纳米薄膜材料特有的微结构使对磁导率的理论计算模拟成为可能。控制磁性纳米颗粒膜的电磁参数对提高薄膜性能非常关键,通过理论计算微波磁导率可以指导薄膜材料设计和工艺优化,从而提高实验效率[4-6]。在此,本文作者在实验研究Co-A1-O磁性纳米颗粒膜微波磁谱基础上,结合Landau-Lifshitz-Gilbert理论和Bruggeman 有效媒质理论,计算模拟该类纳米颗粒膜的有效磁导率,计算分析饱和磁化强度、各向异性场、阻尼系数和磁性相体积分数对磁性纳米颗粒膜磁导率的影响。
1 实验
使用JZCK-450SF型磁控溅射镀膜设备,采用双靶溅射技术制备Co-A1-O磁性纳米颗粒膜。Ar和O2分别作为溅射气体和工作气体, Ar和O2流量分别为 1×10-6和0.167×10-6 m3/s,基片旋转速度为30 r/min。靶基距为10 cm,沉积时间为1 h,工作气压为1 Pa。靶材是纯度为99.99%的Co和Al靶,Al靶的溅射功率固定为30 W,Co靶的溅射功率分别为10,20,30和40 W,溅射时间为60 min。采用Alpha-StepIQ台阶仪测量薄膜样品厚度,使用原子力显微镜(AFM)观测薄膜形貌,采用微带线法在AV3629矢量网络分析仪测量系统中测试薄膜试样微波复磁导率的频谱特性。
2 实验结果与讨论
2.1 表面形貌
图1所示为不同Co溅射功率条件下制备的Co-Al-O薄膜的表面形貌。样品的表面粗糙度依次为2.035,2.582,2.484和2.096 nm。根据溅射时间和台阶仪测得厚度,计算得溅射率依次为1.52,2.03,2.42和2.63 nm/min。制备薄膜试样A和B使用的Co靶溅射功率较小,纳米颗粒膜中的颗粒粒度较均匀;制备薄膜试样C和D使用的Co靶溅射功率较大,颗粒膜的磁性颗粒粒度很不均匀,且大颗粒间有搭接现象,也有磁性小颗粒嵌入介质相中,相分布不太均匀,可能是溅射功率增大、粒子动能增加,使原子在基底表面的移动速率增加,导致颗粒生长速率增大,加速了粒子接合;另一方面,部分能量高的粒子会在撞击点位上产生缺陷,使这些点位的结合能比邻近位高,成为优先成核的点位。薄膜边界的结构不均匀可能来源于压力/张力、重构、位错等内在因素及非理想配比、扩散等外在因素[7],这种结构的差异会引起自旋无序状态存在,对薄膜自旋极化输运和磁性能产生较大影响,从而影响其微波磁导率。
2.2 微波磁导率
不同Co靶溅射功率制备的Co-Al-O磁性纳米颗粒膜试样0.5~5.0 GHz的微波磁谱如图2所示。从图2可见:制备的Co-Al-O磁性纳米颗粒膜试样在0.5~5.0 GHz呈现明显的共振型磁谱。由于包覆在Co磁性颗粒周围的Al2O3介质相很薄,网状分布的介质相产生很多钉扎位点,在薄膜生长过程中可有效抑制磁性金属颗粒长大,使磁性合金颗粒均匀细化,使得磁性颗粒间交换相互作用增强,有利于获得高微波磁导率[8]。表1所示为从上述薄膜试样磁谱获得的磁参数值,可见:薄膜试样D的共振频率最低,但其共振线宽Δf最大;薄膜试样C的共振频率比薄膜试样B的有所提高;随溅射功率增加,薄膜试样的共振线宽Δf增加;薄膜试样B同频率点的μ″比薄膜试样A的μ″有较大提高。

图1 不同Co靶溅射功率制备的试样的原子力显微形貌照片
Fig.1 AFM images of Co-Al-O films sputtered with different Co powers
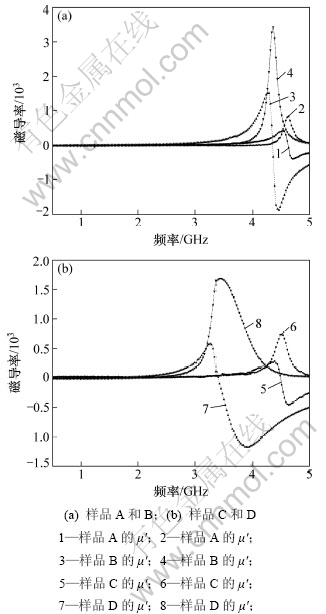
图2 不同Co靶溅射功率制备的薄膜试样的微波磁谱
Fig.2 Complex permeability spectra of Co-Al-O films prepared by different Co power
表1 薄膜试样的磁参量
Table 1 Magnetic parameters of samples
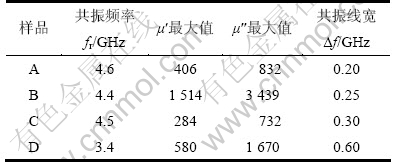
根据Snoek定律[9]fr=(γ/2π)·(4πMsHk)1/2,磁性材料的共振频率主要与饱和磁化强度和各向异性场相关,随二者乘积增大而增大。薄膜试样D的各向异性场最低,是导致其共振频率下降的主要原因。由原子力显微(AFM)观测分析知:薄膜试样D的颗粒粒度和形状不均匀性明显,可能出现磁畴结构改变和畴壁数量增加,造成薄膜的各向异性场 Hk减小;此外,随着Co靶溅射功率增加,弥散分布于Al2O3非晶相中的Co颗粒的晶向趋于无规取向,近邻晶粒的易磁化方向的夹角大,晶粒间交换相互作用也可能减少体系的有效各向异性。薄膜试样C的共振频率比薄膜试样B的高,可能与其具有较高的Ms有关。
共振线宽Δf逐渐增加的原因可能是随Co含量增加,即磁性金属体积分数增大,颗粒间因金属颗粒电导引起的涡流损耗和因分布电容效应导致的弱位移电流涡流损耗增加,从而导致磁导率的共振线宽增大。制备薄膜试样A时的使用的溅射功率较小,Co含量低,由于磁性相偏少、Al2O3非晶相增多导致微结构效应,降低了磁性颗粒的粒径,使颗粒间的相互作用减弱;此外,由于多数Co磁性颗粒被Al2O3非晶相包覆,使磁性粒子与Al2O3相的界面大大增加,并使得毗邻Al2O3的表层Co原子的磁矩因界面能而严重扭变,因此,磁性粒子表层可能出现部分非磁性相,也使共振频率附近μ″减小[10]。
3 磁性纳米颗粒膜磁谱的计算模拟
3.1 磁谱计算方法
由Landau-Lifshitz-Gilbert方程[11],采用线性近似的方法求得磁性颗粒的复磁导率μ为:
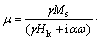
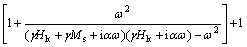 (1)
(1)
其中:Ms为饱和磁化强度;Hk为各向异性磁场强度;γ为旋磁比,取值为2×105 Hz·m/A;ω=2πf,f为频率;α为无量纲的阻尼系数。
通常磁性纳米颗粒膜中磁性金属含量较高,微粒间的相互作用较强,可以采用Bruggeman平均场理论来研究颗粒膜复合体的等效电磁参量,薄膜有效磁导率的Bruggeman方程为:
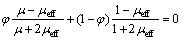 (2)
(2)
其中:φ为磁性颗粒的体积分数;μ为单个磁性颗粒的磁导率;μeff为薄膜的有效磁导率。通过式(1)和(2)以及典型的薄膜参数可以计算磁性纳米颗粒膜的有效磁导率。
3.2 电磁参数对薄膜磁导率的影响
由公式计算不同饱和磁化强度对薄膜磁导率的影响如图3所示。计算取φ=0.5,α=0.008,Hk=10 kA/m,Ms分别为1.4,1.6和1.8 MA/m。Ms增高使颗粒膜起始磁导率增大,共振频率附近的μ′和μ″都增大,共振频率fr也明显提高。薄膜试样C的共振频率与薄膜试样B的相比有所增加,可能与Ms的增大有关[12]。原子力显微镜分析显示薄膜试样C表面有大颗粒团聚,而薄膜试样B的颗粒粒度较均匀。
不同磁各向异性场对磁导率的影响如图4所示。计算取Ms=1.4 MA/m,φ=0.5,α=0.008,Hk分别为8,10和12 kA/m。从图4可见:随着Hk增大,薄膜的起始磁导率降低,fr明显提高,但μ′和μ″也降低。随机分布的磁性纳米晶粒之间的交换耦合相互作用导致有效磁各向异性发生变化[13],与实验发现的薄膜试样D的共振频率显著下降源于Hk的减小现象一致。各向异性场的变化可能与颗粒间的相互作用强度、颗粒粒度、颗粒间距、原子对的方向有序等因素有关[14]。
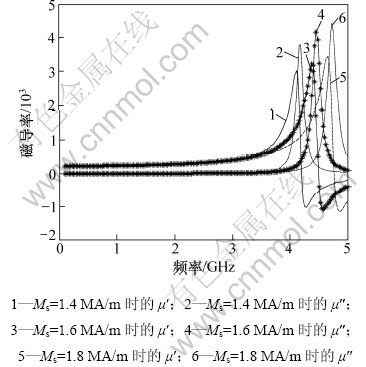
图3 饱和磁化强度Ms对磁导率的影响
Fig.3 Complex permeability spectra with different Ms
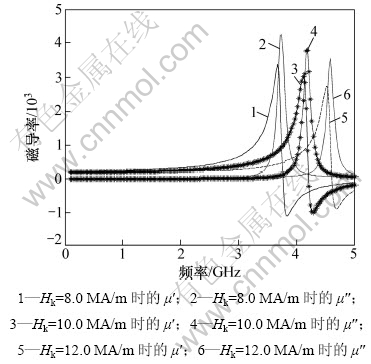
图4 磁各向异性场Hk对磁导率的影响
Fig.4 Complex permeability spectra with different Hk
不同阻尼系数对磁导率的影响曲线如图5所示。计算选取Ms=1.4 MA/m,Hk=10.0 MA/m,φ=0.5,α分别取0.003,0.006和0.009。从图5可见:随着α的增大,μ″的共振线宽Δf明显变宽;与实验发现的随Co靶溅射功率增大导致阻尼系数增大,从而使薄膜的共振线宽Δf逐渐变宽的现象一致。
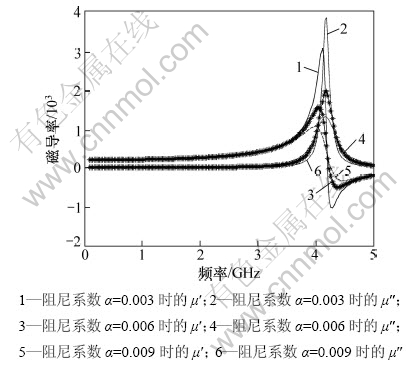
图5 阻尼系数α对磁导率的影响
Fig.5 Complex permeability spectra with different α
不同磁性金属Co的体积分数对磁导率的影响如图6所示。计算选取Ms=1.6 MA/m,α=0.009,Hk=10.0 kA/m,φ分别取0.5,0.6和0.7。从图6可见:随磁性相体积分数增大,薄膜的起始磁导率升高[15],fr无明显变化,共振频率附近μ′和μ″增加,与实验结果基本一致。
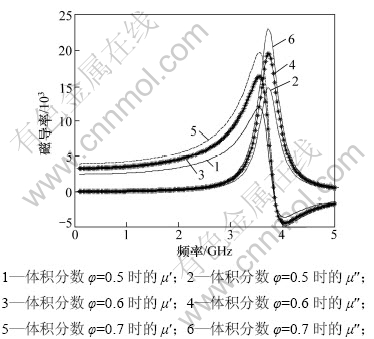
图6 体积分数φ对磁导率的影响
Fig.6 Complex permeability spectra with different φ
4 结论
(1) 制备薄膜试样使用的Co靶溅射功率越大,使近邻晶粒易磁化方向的夹角变大,晶粒间交换相互作用可能减少体系的有效各向异性,造成共振频率变低。实验结果与计算模拟发现的Hk减小导致fr明显降低的趋势基本一致。
(2) 制备工艺导致的Co-A1-O磁性纳米颗粒膜的微结构和微观形貌方面的差异,使薄膜的磁性和微波磁谱出现明显差异;实验现象与计算模拟所得结果基本一致。
(3) Co靶溅射功率提高,可导致颗粒间因分布电容效应引起的弱位移电流涡流损耗增加,导致薄膜磁谱的共振线宽Δf增加。实验结果与模拟阻尼系数增大导致磁谱共振线宽增大的趋势基本一致。
(4) 磁性纳米颗粒膜材料的本征特性、微结构、均匀性、杂质性质和含量、各向异性等对其微波磁导率有重要影响,且这些因素之间构成复杂关联关系。理论计算模拟结果对设计制备纳米颗粒膜具有一定指导意义。
参考文献:
[1] Ohnuma S, Lee H J, Kobayashi N, et al. Co-Zr-O nano-granular thin films with improved high frequency soft magnetic properties[J]. IEEE Transaction on Magnetics, 2001, 37(41): 2251-2254.
[2] Tetsuya O, Toru A, Jun K, et al. Development of high-performance magnetic thin film for high-density magnetic recording[J]. Electrochimica Acta, 2005, 50(23): 4576-4579.
[3] Sulitanu N, Br?nza F. Excellent soft magnetic two-phase nanocrystalline films for various magnetic devices[J]. Sensors and Actuators A: Physical, 2003, 106(1/3): 212-216.
[4] Yang X L, Ruan C L. High frequency properties of Ni75Fe25-SiO2 granular thin films with very high resistivity[J]. Materials Letters, 2007, 61(3): 908-911.
[5] Xiao Y H, Ge S H, Zhang B M, et al. Fabrication and magnetic properties of Fe65Co35-B2O3 granular films for high frequency application[J]. IEEE Transactions on Magnetics, 2009, 45(6): 2770-2772.
[6] Jen S U, Wu T C, Liu C H. Piezoresistance characteristics of some magnetic and non-magnetic metal films[J]. Journal of Magnetism and Magnetic Materials, 2003, 256(1/2/3): 54-59.
[7] Sasaki S, Saito S, Takahashi M. Microstructure and magnetic properties of Co-SiO2 granular film deposited using sintered targets made from Co, Si, and Co-oxide compounds[J]. Journal of the Magnetics Society of Japan, 2009, 33(4): 362-368.
[8] 邓联文, 周克省, 江建军. 电导率对纳米磁性金属膜微波吸收性能影响[J]. 中南大学学报: 自然科学版, 2008, 39(1): 59-63.
DENG Lian-wem, ZHOU Ke-sheng, JIANG Jian-jun. Infulence of conductivity on microwave absorbing ability of nanostructural magnetic metallic film[J]. Journal of Central South University: Science and Technology, 2008, 39(1): 59-63.
[9] Kenji I, Suzuki T, SatoT. CoFeSiO/SiO2 multilayer granular films with very narrow ferromagnetic resonant linewidth[J]. IEEE Transactions on Magnetics, 2009, 45(10): 4290-4293.
[10] Yamagishi Y, Honda S, Inoue J. Numerical simulation of giant magnetoresistance in magnetic multilayers and granular films[J]. Physical Review B: Condensed Matter and Materials Physics, 2010, 81(5): 54445-54449.
[11] Voogt F C, Palstra T T M, Niesen L, et al. Superparamagnetic behavior of structural domains in epitaxial ultrathin magnetite films[J]. Physical Review B: Condensed Matter and Materials Physics, 1998, 57(14): 8107-8110.
[12] Ohnuma S, Fujimori H. FeCo-Zr-O nanogranular soft-magnect thin films with a high magnetic flux density[J]. Applied Physics Letter, 2003, 82(6): 946-948.
[13] Morikawa T, Suzuki M, Taga Y. Improvement of soft magnetic properties of Co-Cr-O film by additional X(=Rh, Ir, Ag, or Au)[J]. Journal of Applied Physics, 1998, 83(5): 6664-6667.
[14] Ikeda K, Kobayashi K, Fujimoto M. Microstructure and magnetic properties of (Co-Fe)-Al-O thin films[J]. Journal of America Ceramic Society, 2002, 85(1): 169-173.
[15] Li S D, Huang Z G, Duh J, et al. Ultrahigh-frequency ferromagnetic properties of FeCoHf films deposited by gradient sputtering[J]. Applied Physics Letter, 2008, 92(6): 92501-92505.
(编辑 陈灿华)
收稿日期:2011-02-01;修回日期:2011-05-02
基金项目:国家重点基础研究发展计划(“973”计划)项目(2011CB605804);湖南省自然科学基金资助项目(10JJ5049);粉末冶金国家重点实验室开放基金资助项目(2010年、2011年)
通信作者:邓联文(1969-),男,湖南邵阳人,博士,副教授,从事电子材料研究;电话:13787206916;E-mail:dlw626@163.com