J. Cent. South Univ. Technol. (2011) 18: 666-671

DOI: 10.1007/s11771-011-0745-z

Pneumatic resistance network analysis and dimension optimization of high pressure electronic pneumatic pressure reducing valve

XU Zhi-peng(徐志鹏)^{1, 2}, WANG Xuan-yin(王宣银)¹

1. State Key Laboratory of Fluid Power Transmission and Control, Zhejiang University, Hangzhou 310027, China;

2. College of Metrology and Measurement Engineering, China Jiliang University, Hangzhou 310018, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: The structure and working principle of a self-deigned high pressure electronic pneumatic pressure reducing valve (EPPRV) with slide pilot are introduced. The resistance value formulas and the relationship between the resistance and pressure of three typical pneumatic resistances are obtained. Then, the method of static characteristics analysis only considering pneumatic resistances is proposed, the resistance network from gas supply to load is built up, and the mathematical model is derived from the flow rate formulas and flow conservation equations, with the compressibility of high pressure gas and temperature drop during the expansion considered in the model. Finally, the pilot spool displacement of 1.5 mm at an output pressure of 15 MPa and the enlarging operating stroke of the pilot spool are taken as optimization targets, and the optimization is carried out based on genetic algorithm and the model mentioned above. The results show that the static characteristics of the EPPRV are significantly improved. The idea of static characteristics analysis and optimization based on pneumatic resistance network is valuable for the design of pneumatic components or system.

Key words: high pressure; pressure reducing valve; pneumatic resistance; dimension optimization; genetic algorithm

1 Introduction

In pneumatic or hydraulic systems, all structures or components that hinder the fluid flowing could be regarded as resistances, such as pipes, valve ports, and orifices [1]. In hydraulic field, there has been systematic research and mature application. BACH? [2] proposed a general method to analyze the characteristics of various hydraulic resistance networks based on electro-hydraulic analog, and this method has become the research foundation of hydraulic resistance network [3]. LU and HU [4] developed a proportional pressure valve with direct detection by the theory of hydraulic resistance network, and the control characteristics of the valve have been greatly improved. HU et al [5-6] proposed the concept of π bridge hydraulic resistance network, and they also developed a G type π bridge pressure relief valve. In pneumatic field, there have also been some investigations. XUE [7] analyzed the charge and discharge characteristics as well as the frequency response of pneumatic resistances and capacitances, and applied this technology in many technical reforms. LIU et al [8] established the model of pneumatic resistances, capacitances and inductances of a pneumatic stripping system, and compared them with the LRC circuit in
physics. XU et al [9] discussed the influence of pneumatic resistances and capacitances on the characteristics of a pressure reducing valve. However, there has been less research on the analysis of various pneumatic resistances, pressure-pneumatic resistance characteristics or optimization based on pneumatic resistances.

A high pressure electronic pneumatic pressure reducing valve (EPPRV) has been developed [10-11], but the static characteristics like quiescent operating point and operating stroke of the pilot spool leave much to be desired, so the EPPRV needs to be optimized. In static characteristics analysis, only the pneumatic resistances need to be considered, while parameters like the pneumatic capacitances and inductances that influence the dynamic characteristics need not. Hence, we research the characteristics of pneumatic resistances thoroughly and use them for dimension optimization of the EPPRV.

As many structural parameters are involved, and the pneumatic system is strongly nonlinear, traditional methods are not suitable for the multiple objectives optimization in this study [12-13]. Genetic algorithm has been wildly used in engineering since it came into being. It is practical, efficient and strongly robust when being used for optimization [14-15], hence it is applied for the optimization of the EPPRV.

2 Structure of EPPRV

Structure of the EPPRV is shown in Fig.1. It mainly consists of the piston structured main valve and the slide pilot valve. The EPPRV can be divided into inlet chamber (I), outlet chamber (O), pressure regulating chamber (R), feedback chamber (F) and pilot chamber (P) by pressure zones, and their corresponding pressure is p_j (j=i, o, r, f, p). Pressure regulating is achieved by adjusting the opening of the pilot spool x₀: increase x₀, more gas flows from I-chamber, through P-chamber and into R-chamber, then pressure in R-chamber p_r increases, and the opening of the main spool x₁ increases, so output pressure p_o rises; on the contrary, decrease x₀, p_o drops. R-chamber and O-chamber are connected with a fixed hole whose diameter is d_r. Both the pilot spool and the main spool are under dynamic balance during working.

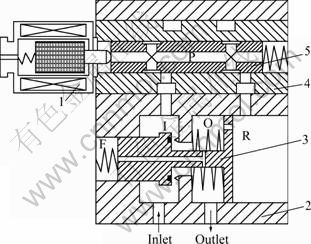
Fig.1 Structure of EPPRV: 1—Proportional electromagnet; 2— Valve body; 3—Components of main spool; 4—Pilot sleeve;  5—Pilot spool

Gas flow in the pilot valve and throttle windows are shown in Fig.2. Figure 2(a) shows the diagram of gas flow. The inlet of the pilot valve is connected with I-chamber of the main valve, the outlet of the pilot valve is connected with R-chamber of the main valve, and d_p is the diameter of the pilot spool. When the pilot valve is working, the gas flows from the inlet throttle window to the outlet throttle window and forms throttle flow q_tip and q_tpr. For the existence of annular clearance between pilot spool and pilot sleeve, there will be leakage gas that flows under the pressure difference between p_i and p_p as well as p_p and p_r, and they are denoted as clearance flow q_gip and q_gpr. The clearance lengths are l₁+x₀ and l₂+x₀, respectively. Figure 2(b) shows the schematic diagram of the rectangular throttle windows of the pilot sleeve, where w₁ and w₂ are the widths of the inlet and outlet windows, respectively.

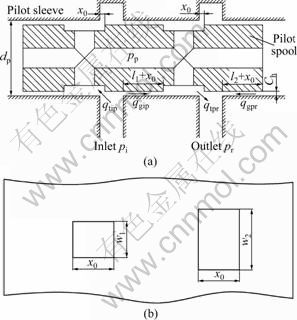
Fig.2 Gas flow in pilot valve (a) and throttle windows (b)

3 Pneumatic resistances and resistance net- work of EPPRV

Similar to electric resistance and hydraulic resistance, the pneumatic resistance is defined as

                                                                        (1)

where Δp is the pressure difference between two ends of the resistance, q is the mass flow rate. The pneumatic resistances can be mainly divided into throttle resistance, clearance resistance and slender hole resistance according to different structures, and their flow rate-pressure characteristics and resistance values are listed in Table 1 [16-17].

In Table 1, q_t, q_g and q_h are the mass flow rates through the throttle orifice, annular clearance and slender hole, respectively; α is the coefficient of contraction; S is the passage area of the throttle orifice; p₁ and p₂ are the upstream and downstream pressures of the resistance; d_g is the diameter of the inner cylinder of annular clearance; C_h is the height of annular clearance; μ is the dynamic viscosity of air; l_g is the length of annular clearance; R is the gas constant of air; T₁ is the temperature of upstream air; d is the diameter of slender hole; l is the length of slender hole; φ(p₂, p₁) is expressed as

    (2)

where k is the specific heat ratio of air, and b is the critical pressure ratio of the EPPRV.

Table 1 Flow rate-pressure characteristics and resistance values of three typical pneumatic resistances

The values of pneumatic resistances are coupled with both the upstream and downstream pressures. Both the values of clearance resistance and slender hole resistance are inversely proportional to the sum of upstream and downstream pressure, while the expression of throttle resistance is so complicated that it is both associated with the difference and ratio of upstream to downstream pressure. Take a throttle resistance R_t with the diameter of 1 mm and a clearance resistance R_g with the cylinder diameter of 10 mm, the clearance length of 10 mm and the clearance height of 10 μm for example, the relationships of their resistance values with different combinations of upstream and downstream pressures are shown in Fig.3.

Fig.3 Relationship between pneumatic resistances and pressure: (a) R_t; (b) R_g

When the EPPRV works steadily, the pneumatic resistance network from air supply to atmosphere is shown in Fig.4. It consists of four variable resistances and three fixed resistances (referring to flow area rather than resistance value). The first character of footnote stands for the resistance type and the last two characters stand for the chambers before and after the resistance. Take R_tip for example, it stands for the throttle resistance between the I-chamber and P-chamber. The load of the EPPRV is a fixed throttle hole through which the air flows from the outlet of the EPPRV to atmosphere p_a, and the diameter of the fixed hole is d_l.

Fig.4 Pneumatic resistance network of EPPRV

4 Mathematical model of pneumatic resistance network

A direct quantitative analysis with pneumatic resistance value is not suitable for multi-resistance network, because the resistance values are coupled with both the upstream and downstream pressures, and the pressures of intermediate nodes in the resistance network are also unknown. Hence, we combine the flow rate formulas of each pneumatic resistance and the flow rate conservation formulas at each pressure node to build the mathematical model of the resistance network [18-19].

The state equation of real gas can be expressed as

pV=ZmRT                                        (3)

where Z is the compressibility factor of air, and it changes as p or T changes and can be looked up from Ref.[20].

The state changing process of gas in chambers is adiabatic, and the following equation is obeyed:

                                                              (4)

The temperature in j chambers T_j (j= i, o, r, f) can be deduced from Eqs.(3) and (4) as

                                                    (5)

The throttle flow rate from the R-chamber of the main valve through the throttle window to the P-chamber of the pilot valve is

                                 (6)

The clearance flow rate from the I-chamber of the main valve through the annular clearance to the P-chamber of the pilot valve is

                                          (7)

The throttle flow rate from the P-chamber of the pilot valve the through throttle windows to the R-chamber of the main valve is

                              (8)

The clearance flow rate from the P-chamber of the pilot valve through the annular clearance to the R-chamber of the main valve is

                              (9)

The throttle flow rate from the R-chamber of the main valve through the fixed hole to the O-chamber of the main valve is

                          (10)

The flow conservation equations of gas that flows from the I-chamber of the main valve through the pilot valve to the O-chamber the main valve are

                                                (11)

                                                          (12)

The throttle flow rate from the I-chamber through the main orifice to the O-chamber of the main valve is

                            (13)

where d_m is the diameter of the main orifice which is shaped as a cylindrical surface.

The throttle flow rate from the O-chamber of the main valve through the load to atmosphere is

                         (14)

The flow rate of the load is the sum of flow rate of the pilot valve and the main valve:

                                                          (15)

The main spool remains static when the EPPRV is under steady state, and its force equilibrium equation is expressed as

                    (16)

where S_j is the gas action area on the main spool in j chamber (j= i, o, r, f), K_m and C₀ are the stiffness and pre-tightening force of main spring, respectively.

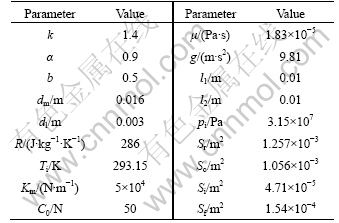
Equations (2) and (5)-(16) constitute the mathematical model for static characteristic analysis of the EPPRV. Displacement of the pilot spool, pressure at each node and flow rate through each resistance can be solved by the model when p_i, p_o and the structural parameters are given. The structural parameters involved in these equations except optimization variables are listed in Table 2.

Table 2 Values of simulation parameters

5 Dimension optimization based on genetic algorithm

The rated stroke of the proportional electromagnet is 0-3 mm, the designed output pressure range of the EPPRV is 5-25 MPa (p_i=31.5 MPa). The linearity in the middle region of either the displacement-force curve or the current- force curve is much better than that of other parts, hence we choose the middle stroke of the electromagnet as the target operating stroke of the pilot valve in the optimization, that is, the displacement of the pilot valve is x_0-15=1.5 mm at the typical operating point p_o=15 MPa, and the operating stroke of the pilot valve is x_0-25-x_0-5=2 mm. The optimization target function is defined as

J=k₁×(x_0-15-0.0015)²+k₂×(x_0-25-x_0-5-0.002)²            (17)

where k₁ and k₂ are the weighting coefficients, which are set as k₁=10 and k₂=1 according to their importances.

The preliminary analysis of the resistance network and mathematical model shows that there are mainly five parameters influencing the displacement of pilot spool: C_h, w₁, w₂, d_p and d_h, where the annular clearance C_h is difficult to be ensured during processing. Hence, w₁, w₂, d_p and d_h are chosen as the optimization variables and their initial values are: w₁=0.6 mm, w₂=0.6 mm, d_p=    6 mm, d_h=1.6 mm. Taking the processing capacity and the dimension size of the main valve into consideration, the variables are limited as: 0.2 mm≤w₁≤2 mm, 0.2 mm≤ w₂≤ 2 mm, 5 mm≤d_p≤20 mm, 0h≤3 mm.

The Matlab genetic algorithm toolbox proposed by the University of Sheffield is chosen for the optimization. The initial population size is M=30, the probability of crossover is P_c=0.9, and the probability of mutation is P_m=0.005. The optimization results with different C_h values are listed in Table 3.

Table 3 Dimension optimization results

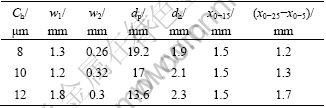
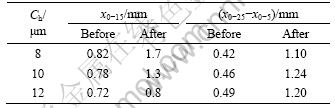
It can be seen from Table 3 that, when x_0-15=1.5 mm is ensured, the operating stroke of the pilot spool will increase as C_h grows, but the target of 2 mm cannot be satisfied. Considering the results with different C_h, we choose the values of these variables as: w₁=1.5 mm, w₂=0.3 mm, d_p=15 mm and d_h=2 mm. Then, we calculate x_0-15 and (x_0-25-x_0-5) with the variables before and after the optimization, and the results are listed in Table 4. It can be seen that the operating stroke of the pilot valve (x_0-25-x_0-5) is enlarged by more than two times, while x_0-15 which varies from 0.8 to 1.7 mm is greatly affected by C_h, so C_h should be controlled slightly less than    10 μm during the processing to ensure that x_0-15 gets close to 1.5 mm.

Table 4 Values of x_0-15 and x_0-25-x_0-5 before and after optimization

6 Conclusions

1) The components shape and parameters of pneumatic capacitances could be ignored for the static characteristic analysis of components or system, so that the analysis could be greatly simplified.

2) Direct quantitative analysis with pneumatic resistance value is not suitable for multi-resistance network, because resistance values are coupled with both upstream and downstream pressure, and the pressure of intermediate nodes in the resistance network is also unknown.

3) When the EPPRV works steadily, the pneumatic resistance network from air supply to atmosphere consists of four variable resistances and three fixed resistances (referring to flow area rather than resistance values), including throttle resistances and clearance resistances.

4) The values chosen for optimization variables are: w₁=1.5 mm, w₂=0.3 mm, d_p=15 mm, d_h=2 mm. After the optimization, the operating stroke of the pilot valve (x_0-25-x_0-5) is enlarged by more than two times, while x_0-15 varies a lot as C_h changes. C_h should be controlled slightly less than 10 μm during the processing to ensure that x_0-15 gets close to 1.5 mm.

5) The static characteristic analysis method based on pneumatic resistance network could greatly simplify the mathematic model, while the dimension optimization based on the genetic algorithm is efficient and practical. The method is a valuable reference for the design of the pneumatic components or system.

References

[1] IDELCHIK I E, FRIED E. Handbook of hydraulic resistance [M]. 2nd ed. New York: Hemisphere Publishing House, 1986: 8-20.

[2] BACH? W. Systematics of hydraulic resistance circuit [M]. ZHOU Wen, Transl. Beijing: China Machine Press, 1980: 1-4. (in Chinese)

[3] HU Yan-ping, PENG You-duo, WU Gen-mao. Systematics of hydraulic resistance [M]. Beijing: China Machine Press, 2003: 20-26. (in Chinese)

[4] LU Yong-xiang, HU Da-hong. Electro-hydraulic proportional control technology [M]. Beijing: China Machine Press, 1988: 62-85. (in Chinese)

[5] HU Yan-ping, WEI Jian-hua, GUO Ying-fu, LIU De-shun. The theory and application of bridge hydraulic resistance networks [J]．Transaction of Nonferrous Metals Society of China, 1999, 9(1): 202-206.

[6] HU Yan-ping, HUANG Zhi-chu, LIU De-shun, MAO Zheng-yu. Design theory for g-π bridge relief valve with zero override [J]. Chinese Journal of Mechanical Engineering, 2004, 17(3): 463-465.

[7] XUE Zhi. Pneumatic resistance and capacitance as well as their application [J]. Taiguo Science and Technology, 1991, 2: 47-49, 57. (in Chinese)

[8] LIU Ming-wei, ZHANG Liang-feng, SONG Jing-qi, FU Chang-e, ZHAO Guang-qiang. Application of pneumatic capacity pneumatic inductance and pneumatic resistance on pneumatic peeling-off [J]. Chinese Hydraulic & Pneumatics, 2006, 6: 14-15. (in Chinese)

[9] XU Zhi-peng, WANG Xuan-yin, PI Yang-jun. Numerical simulation of PPRV based on pneumatic bridge networks [C]// Proceeding of the Fifth Fluid Power Transmission and Control. Qinhuangdao: International Academic Publishers Ltd., 2007: 961-964.

[10] WANG Xuan-yin, CHEN Yi-ze, LIU Rong, LIANG Dong-tai. Mechanics and simulation of pneumatic proportional extra-high pressure valve [J]. Journal of Zhejiang University: Engineering Science, 2005, 39(5): 614-617. (in Chinese)

[11] CHEN Yi-ze, WANG Xuan-yin, XU Zhi-peng, TAO Guo-liang. Pilot leakage’s influences on the performances of extra high pressure proportional pneumatic valve [J]. Chinese Journal of Mechanical Engineering, 2005, 18(2): 208-211.

[12] EDMOND R, YILDIRIM H. A high performance pneumatic force actuator system: Part I. Nonlinear mathematical model [J]. Journal of Dynamic Systems, Measurement, and Control, 2000, 122(3): 416-425.

[13] EDMOND R, YILDIRIM H. A high performance pneumatic force actuator system: part II. Nonlinear controller design [J]. Journal of Dynamic Systems, Measurement, and Control, 2000, 122(3): 426-434.

[14] CAROLOS M F, PETER F J. Genetic algorithms for multiobjective optimization: Formulation discussion and generalization [C]// Proceedings of the 5th International Conference on Genetic Algorithms. San Francisco: Morgan Kaufmann Publishers Inc, 1993: 416-423.

[15] WEILE D S, MICHIELSSEN E. Genetic algorithm optimization applied to electromagnetics: A review [J]. IEEE Transactions on Antennas and Propagation, 1997, 45(3): 343-353.

[16] YAO D, BURTON R, NIKIFORUK, NIKIFORUK P, UKRAINETZ P. Research and development of a direct pressure sensing relief valve [C]// Proceeding of the 4th International Conference on Fluid Power Transmission and Control. Beijing: International Academic Publishers Ltd., 1997: 150-155.

[17] SORLI M, FIGLIOLIN G, PASTORELLI S. Dynamic model and experimental investigation of a pneumatic proportional pressure valve [J]. Mechatronics, 2004, 9(1): 78-86.

[18] DASGUPTA K, KARMAKAR R. Modelling and dynamics of single-stage pressure relief valve with directional damping [J]. Simulation Modelling Practice and Theory, 2002, 10: 51-67.

[19] KOICHI I, KENJI K, TOSHIHARU K. Development of simultaneous measurement system for instantaneous density, viscosity and flow rate of gases [J]. Sensors and Actuators A, 2007, 140: 1-7.

[20] WIKIPEDIA. Compressibility factor [EB/OL]. [2010-01-10]. http:// en.wikipedia.org/wiki/Compressibility_factor.

(Edited by YANG Bing)

Foundation item: Project(50575202) supported by the National Natural Science Foundation of China

Received date: 2010-03-04; Accepted date: 2010-05-28

Corresponding author: XU Zhi-peng, PhD; Tel: +86-571-86914565; E-mail: zhp_xu@hotmail.com