DOI: 10.11817/j.issn.1672-7207.2019.11.002
固体氧化物燃料电池数值仿真模型的建立
汤水,张茂贵,贾明,刘宇
(中南大学 冶金与环境学院,湖南 长沙,410083)
摘要:基于COMSOL Multi-physics 5.3a仿真平台,建立三维模型对固体氧化燃料电池进行数值计算。考虑板式固体氧化物燃料电池单体内部的气体流动、组分质量分数、电化学反应过程,研究不同工况下的气体分布、电流密度和极化情况,分析电池长度、工作温度、进气成分对固体氧化物燃料电池工作性能的影响。研究结果表明:固体氧化物燃料电池入口处气体质量分数较大,电化学反应速率也较快;在高电流密度下,入口氧气的质量分数会显著影响电池性能,而在低电流密度下,氧气质量分数不是影响电池电压的主要因素;当电池工作温度升高时,电池内部很多参数会发生变化。
关键词:固体氧化物燃料电池;数值模拟;模型;电流密度;气体分布
中图分类号:TM911.42 文献标志码:A 文章编号:1672-7207(2019)11-2633-12
Establishment of numerical simulation model for solid oxide fuel cell
TANG Shui, ZHANG Maogui, JIA Ming, LIU Yu
(School of Metallurgy and Environment, Central South University, Changsha 410083, China)
Abstract: Based on the COMSOL Multi-physics 5.3a simulation platform, a 3D model for numerical calculation of solid oxide fuel cell was established. With consideration of the gas flow, component mass fraction and electrochemical reaction process inside the slabs solid oxide fuel cell(SOFC) monomer, the gas distribution, current density and polarization under different working conditions were studied, and the influence of cell length, operating temperature and intake composition on the performance of the solid oxide fuel cell was analyzed. The results show that the solid oxide fuel cell inlet gas mass fraction is higher and the electrochemical reaction rate is faster. In the case of high current density, the mass fraction of inlet oxygen significantly affects the battery performance, while in the case of low current density, the oxygen mass fraction is not the main factor affecting the battery voltage. When the working temperature of the battery increases, many parameters inside the battery change.
Key words: SOFC(solid oxide fuel cell); numerical simulation; model; current density; gas distribution
近年来,我国资源与安全环境问题的矛盾日益凸显。在电动汽车大力发展的推动下,燃料电池作为一项清洁高效的尖端技术成为人们研究的焦点。燃料电池是继火电、水电和核电后的第四代发电方式[1],发电不受卡诺循环限制,能量转化效率高达40%~60%,可直接将燃料与氧化剂中储存的化学能转化为电能。以氢氧燃料电池为例[2],在电池阳极侧通入氢气,在电池阴极侧通入氧气,在阴极和阳极的电催化剂的帮助下,氧气在阴极反应区发生还原反应生成水,氢气在阳极反应区发生氧化反应生成氢离子和电子,通过电解质传导离子及电子沿外电路定向移动形成回路,从而形成电流带动负载工作。固体氧化物燃料电池SOFC(solid oxide fuel cell)[3]具有诸多优点,研发和应用大规模的SOFC发电装置系统能有效缓解目前人类面临的能源问题。然而,固体氧化物燃料电池工作温度高,结构紧凑、复杂,工作环境封闭且复杂,通过实际实验来获得其内部状态变化情况和具体位置参数往往极为困难且耗费大量财力和物力。随着计算机计算能力的提高,搭建固体氧化物燃料电池的数学模型、使用计算机数值分析求解来进行仿真实验成为可能。CFD(computational fluid dynamics)方法是分析燃料电池性能的一种重要方法[4-6],它使用数值方法将描述特定流场运动的方程组离散到网格节点上并求出其离散数值解,主要有有限差分法、有限元法、有限容积法等。WEI等[7]提出了基于流量通道设计对堆叠性能影响的数值研究、流路和堆叠布置的新设计,并分析了平面阳极支撑的固体氧化物燃料电池堆的热应力。MANGLIK等[8]在具有不同形状的双极板互连流动通道、由平面阳极支撑的SOFC中同时模拟热和质量传递。黑盒模型基于人工智能,其实现主要依赖于实验数据[9]。SORRENTINO等[10]综合白盒和黑盒模型,提出一种SOFC单电池的灰盒模型。它基于物理关系,根据经验建模,较灵活[11]。这些研究大多以温度、流速等为研究对象,未考虑到内部多物理场耦合情况。为此,本文基于COMSOL Multiphysics数值仿真平台,考虑板式固体氧化物燃料电池内部的气体流动、组分质量分数、电化学反应过程,建立固体氧化物燃料电池的三维模型。
1 固体氧化物燃料电池模型的建立
1.1 研究对象
SOFC工作温度高(600~1 000 ℃),可以快速达到热力学平衡,从而降低对催化剂的要求。其以氧化物离子导电陶瓷材料作为电解质,氧离子作为传输离子,工作原理如图1所示。
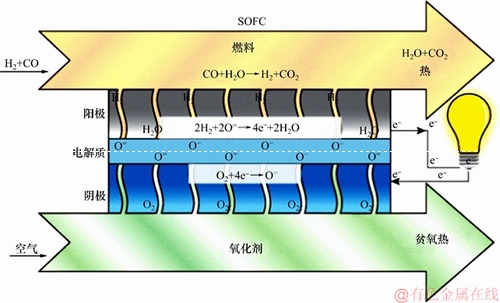
图1 固体氧化物燃料电池工作示意图
Fig. 1 Schematic diagram of solid oxide fuel cell operation
氧化剂(一般为氧气或富氧空气)在阴极反应区内发生还原反应生成O2-:
O2+4e-→2O2- (1)
O2-通过固体电解质输入至阳极反应区,而电子则通过外电路从电池的阳极传输到阴极形成电流。燃料气在阳极反应区内发生氧化还原反应,见下式(以氢气为例):
2H2+2O2-→4H2O+4e- (2)
电池的总反应为
2H2+O2→2H2O (3)
在标准状态下,SOFC单电池电压理论上能达到1.229 V,能量转化效率高达80%。电池的开路电压可用下式计算:
 (4)
(4)
其中:
 (5)
(5)
式中: ,
,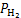 和
和 分别为氧气、氢气和水蒸气分压;R为通用气体常数;F为法拉第常数;
分别为氧气、氢气和水蒸气分压;R为通用气体常数;F为法拉第常数;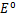 为电池标准电压;
为电池标准电压;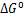 为标准吉布斯自由能。
为标准吉布斯自由能。
工作温度、燃料及氧化剂的种类对单电池的电压和能量转化效率都有很大影响[12]。此外,由于电池中的欧姆极化、电化学极化和浓差极化,电池的实际输出电压与理论值有很大差异。
1.2 模型建立
1.2.1 几何模型
三维模型可以模拟燃料电池内部行为,并且给出关于温度和燃料分布信息[13]。选取固体燃料电池单体作为研究对象,建立SOFC单电池三维模型,如图2所示,具体参数如表1所示。
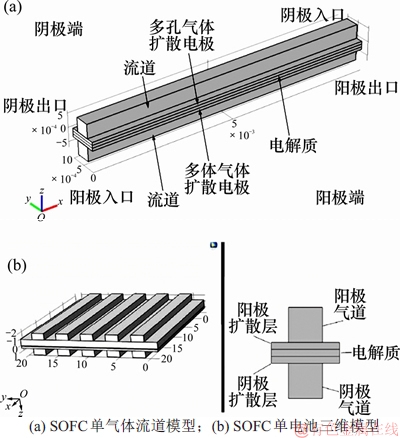
图2 SOFC单气体流道模型和SOFC单电池三维模型
Fig. 2 SOFC single gas channel model and 3D model of SOFC single cell
表1 SOFC模型参数
Table 1 Parameters of SOFC model

1.2.2 模型假设
为简化模型、提高模型的适用型,在模型建立的过程进行如下假设:
1) 本模型反应过程是稳态的,且电池内部各种材料具有各向同性;
2) 温度均匀且在运行过程中保持不变;
3) 压力为标准大气压;
4) 反应气体均为理想气体;
5) 电极内物质对流传递可以忽略。
1.2.3 SOFC单电池三维模型的建立
经分析,模型的反应过程可由Butler-Volmer公式、欧姆定律(描述电子电荷平衡、离子电荷平衡)、Navier-Stokes模型(描述气体通道中的流量分布)、Strokes-Brinkman模型(描述多孔气体扩散电极中的流量)、Maxwell-Stefan扩散和对流模型(描述气体通道和多孔电极中气相的质量平衡),以及边界条件和初始条件构成封闭的方程组来描述。下面详述模型所使用的物理场接口及方程[14-16]。
1.3 物理场分析
1.3.1 二次电流分布
本模型在阴极、电解质和阳极中采用二次电流分布接口,通过二次电流分布接口与模拟质量传递的接口耦合,可描述模型中电流密度分布随浓度变化的变化;通过二次电流分布接口与欧姆定律和电荷守恒耦合,可描述模型中电极和电解质中的电流传导。
将阳极和阴极定义为多孔电极,给定电解质和电极材料电导率、多孔电极反应的温度、平衡电位、相关动力学参数和活性比表面积,设置电池的零电势点和电压初始值。在离子电荷守恒中,假设所有外部边界都是绝缘的,而在内部边界将电流和电势看作是连续变化的。假设阳极和阴极反应区中的电子和离子满足电荷平衡,电荷转移和过电位之间的关系可以用Butler-Volmer公式来描述[17]。
在阳极,氢被氧化形成水,并假设第一电子转移为速率控制步骤,则满足
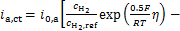
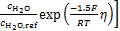 (6)
(6)
式中:i0, a为阳极交换电流密度,A/m2;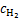 和
和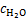 分别为H2和H2O浓度,mol/m3;
分别为H2和H2O浓度,mol/m3;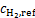 和
和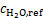 分别为H2和H2O参考浓度,mol/m3;T为温度,K;η为过电位,V。
分别为H2和H2O参考浓度,mol/m3;T为温度,K;η为过电位,V。
对阴极,满足
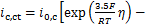
 (7)
(7)
式中:i0,c为阴极交换电流密度,A/m2;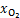 为氧气的摩尔分数,%;
为氧气的摩尔分数,%;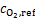 为O2参考浓度,mol/m3。
为O2参考浓度,mol/m3。
过电位η用下式计算:
 (8)
(8)
式中: 为电子电阻引起的欧姆电阻电位,V;
为电子电阻引起的欧姆电阻电位,V;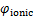 为离子电阻引起的欧姆电阻,Ω;
为离子电阻引起的欧姆电阻,Ω; 为平衡电势差,V。
为平衡电势差,V。
以阳极的入口边界作为零电势点,阴极的入口边界作为电池电势点,Vcell通过下式计算:
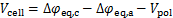 (9)
(9)
式中:Vcell为SOFC工作电压;Vpol为极化电压,V;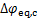 和
和 分别为阴、阳极平衡电势差。
分别为阴、阳极平衡电势差。
在此模型中, 为0 V,
为0 V,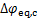 为1 V。当压力一定时,电池电压随电流密度增加而降低,即电压损失会逐渐增大,因电流密度增加导致极化损失和欧姆损失增大;当电流密度较低时,电池反应受电极动力学控制,电压损失以活化极化为主;当电流密度较高时,电化学反应受气体扩散速率控制,电压快速下降。据式(4),温度升高,电池的理想电压会降低,同时,高温有利于增大电解质的离子电导率,减小欧姆极化过电位[18]。
为1 V。当压力一定时,电池电压随电流密度增加而降低,即电压损失会逐渐增大,因电流密度增加导致极化损失和欧姆损失增大;当电流密度较低时,电池反应受电极动力学控制,电压损失以活化极化为主;当电流密度较高时,电化学反应受气体扩散速率控制,电压快速下降。据式(4),温度升高,电池的理想电压会降低,同时,高温有利于增大电解质的离子电导率,减小欧姆极化过电位[18]。
1.3.2 浓物质传递
在阳极和阴极各设1个浓物质传递接口,阳极因变量为H2和H2O的质量分数,阴极因变量为O2,H2O和N2的质量分数。浓物质传递用于研究气体和流体混合物,其中,物质浓度具有相同量级,且都不能被看作是溶剂。混合物的属性依赖于组成,需考虑所有物质的分子和离子之间的相互作用。此接口中包含多组分扩散模型,其中每种物质的扩散驱动力受组成、温度以及压力的影响,用于求解所有参与物质的质量分数,通过对流(粒子随溶液的流动而流动)、扩散(粒子在浓度梯度下的运动)以及电迁移(带电粒子在电场作用下的迁移)来传质。假设电极和气体通道的扩散机制为Maxwell-Stefan模型,给定方程相关参数和初始值,加入多孔电极耦合,输入局部电流源,给定反应电子数和化学计量数,指定气体出口和入口。将气体通道和气体扩散电极壁的边界条件设为零质量通量,设组分和通量的连续性适用于气体扩散电极和气体通道所有界面。
1.3.3 自由和多孔介质流动
在阳极和阴极各设1个自由和多孔介质流动接口,阳极因变量为速度场ua、压力pa,阴极因变量为速度场uc、压力pc。本模型使用弱可压缩Navier-Stokes方程控制气体通道中的气体,用Brinkman方程描述多孔气体扩散电极中的流速,计算单相自由流动与多孔介质连接在一起时的速度场和压力场。
将电极和气体通道的自由和多孔介质流动的物理模型设为可压缩流(马赫数Ma<0.3),给定流体的动力黏度和密度;设定多孔基体属性,给定孔隙率、渗透率;加入多孔电极耦合,输入局部电流源,给定反应电子数、化学计量数。指定流体出口和入口,设置压力,使入口处轻微过压以驱动气体流动,出口处选择法向流,设置边界条件为滑移。耦合以上几个接口,可描述SOFC单电池的内部电化学反应过程和传质过程。
2 结果讨论
2.1 模型验证
确定模型的物理场、内部参数和网格划分方式,分别对极化电压、入口氧气质量分数、工作温度、单电池长度进行参数化扫描和模拟计算。考察电池内部气体分布、电流密度分布、极化情况。将模拟所得结果与实验结果进行对比,以验证模型的有效性[19-20]。该三维模型剖分网格为36 288个,满足研究要求。
2.2 不同极化电压下电池内部状态
为研究不同极化值下(即电池电压不同时)电池内部气体分布情况以及电流密度分布情况,应用上述数学模型,在温度为800 ℃,压力为1×105 Pa,单电池长度为0.01 m,入口燃料气体为40%(质量分数,下同)氢气与60%水蒸气,阴极气体为15%氧气与37%水蒸气与58%氮气,其他参数见表1,计算不同入口氧气质量分数下的阴阳极气体分布情况。
图3所示为不同极化值时电解质平面上电流密度及分布。从图3可见:当极化值为0.05 V即电池电压为0.95 V时,电流集中分布在电池左端;随着极化值不断增大,电池电流密度也随之增大;电流开始集中分布于电池右端,且随极化值进一步增大,电池密度峰值范围进一步扩大,分布更加均匀,由右端向中部逐渐减少;当电流密度较低时,电池反应受电极动力学控制,电压损失以活化极化为主;当电流密度较高时,电化学反应受气体扩散速率控制,电压快速下降;因氧气耗尽,电流密度分布很不均匀,集中在右端阴极入口处。
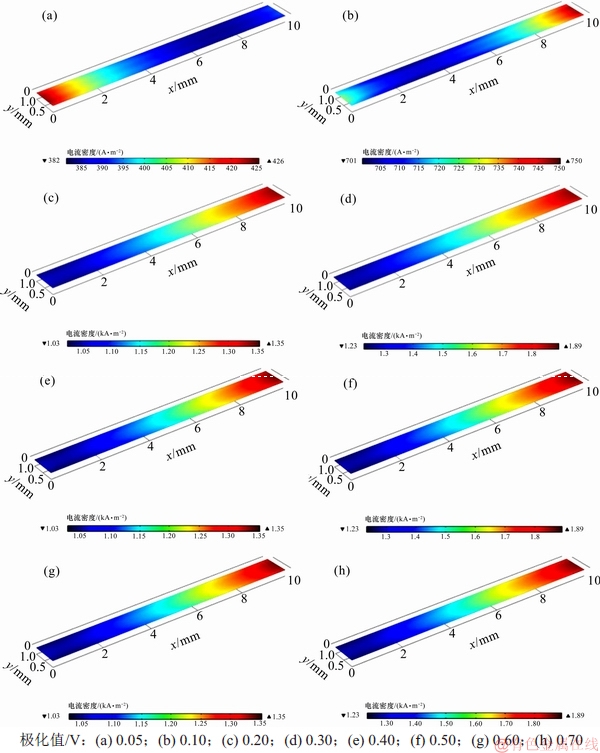
图3 不同极化值下电解质平面上电流密度及分布
Fig. 3 Current density and distribution on electrolyte plane under different polarization values
在极化值为0.5 V即电池电压为0.5 V时,氧气摩尔分数在阴极和气体流道的分布情况如图4所示。从图4可见:氧气由电池右端向电池左端扩散,扩散非均匀。氧气在阴极的消耗量表明阴极发生反应的程度。
当极化值为0.5 V时,氢气摩尔分数在气体流道和阳极中的分布情况如图5所示。从图5可见:与氧气的分布类似,氢气在阳极的分布也呈现沿输入口向出口方向减少的现象。
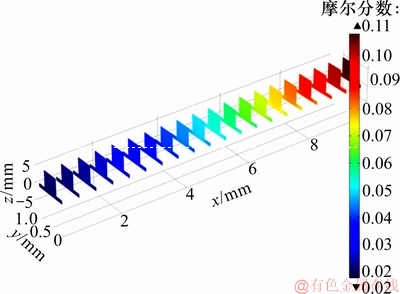
图4 氧气的摩尔分数分布
Fig. 4 Mole fraction distribution of oxygen
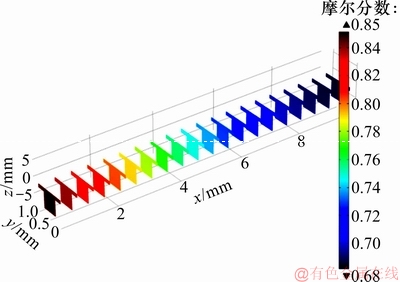
图5 氢气的摩尔分数分布
Fig. 5 Mole fraction distribution of hydrogen
2.3 入口氧气质量分数对电池的影响
为研究不同入口氧气质量分数下电池内部气体分布情况以及电流密度分布情况,在温度为800 ℃,压力为1×105 Pa,极化值为0.5 V,单电池长度为0.01 m,入口燃料气体为40%氢气与60%水蒸气,其他参数按表1设置的条件下,计算不同入口氧气质量分数下的阴阳极气体分布情况,分析入口氧气质量分数对极化曲线的影响,仿真结果如图6和图7所示。
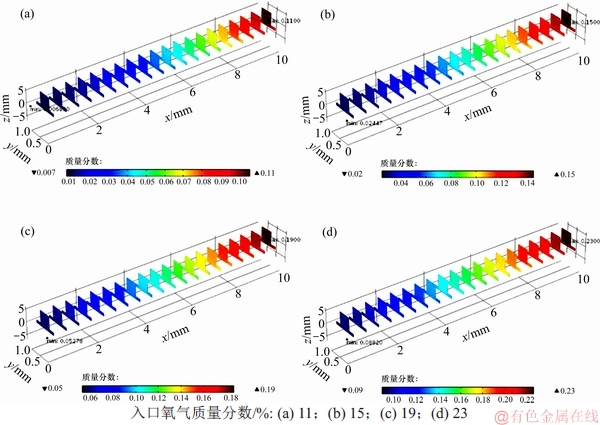
图6 氧气分布随入口氧气质量分数的变化
Fig. 6 Oxygen distribution varies with inlet oxygen mass fraction
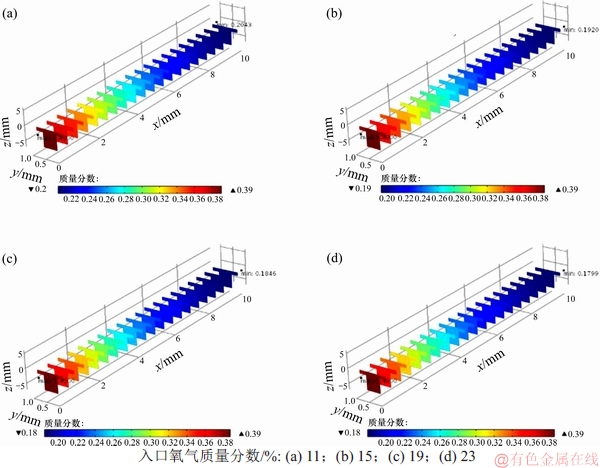
图7 氢气分布随入口氧气质量分数的变化
Fig. 7 Hydrogen distribution varies with inlet oxygen mass fraction
从图6和表2可看出:随着入口氧气质量分数增加,出口氧气最小质量分数也随之增加,且在本模型中明显呈现线性增加的趋势。
表2 入口氧气质量分数对出口氧气最小质量分数的影响
Table 2 Effect of inlet oxygen mass fraction on the minimum mass fraction of outlet oxygen

图7所示为不同入口氧气质量分数时氢气质量分数在阳极和气体流道中的分布。质量分数为40%的氢气从电池左端输入,从电池右端流出,如表3所示。
表3 入口氧气质量分数对出口氢气最小质量分数的影响
Table 3 Influence of inlet oxygen mass fraction on the minimum mass fraction of outlet hydrogen
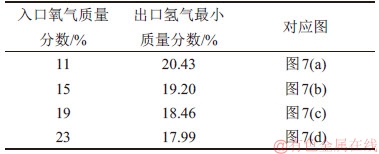
随入口氧气质量分数增加,出口氢气最小质量分数也随之减少,且在本模型中呈现线性减少的趋势,但变化不大。由表3可知:当氧气质量分数为11%~23%时,氢气消耗基本相同,即在模型中入口氢气的质量只要达到40%就可保证电化学反应过程不受氢气质量分数的限制。
不同入口氧气质量分数下极化曲线如图8所示。从图8可见:在高电流密度下,入口氧气的质量分数会显著影响电池性能;而在低电流密度下,氧气质量分数不是影响电池电压的主要因素。
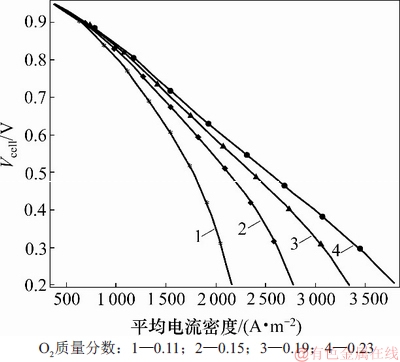
图8 不同入口氧气质量分数下极化曲线
Fig. 8 Polarization curves at different inlet oxygen mass fractions
2.4 工作温度对电池的影响
应用上述数学模型,为研究SOFC在不同工作温度(800~1 000℃)下电池电压与功率随电流密度的变化趋势,在压力为1×105 Pa,单电池长度为0.01 m,燃料气体为40%氢气与60%水蒸气,阴极气体为15%氧气、37%水蒸气和58%氮气,其他参数按表1设置的条件下进行计算,仿真结果分别如图9和图10所示。
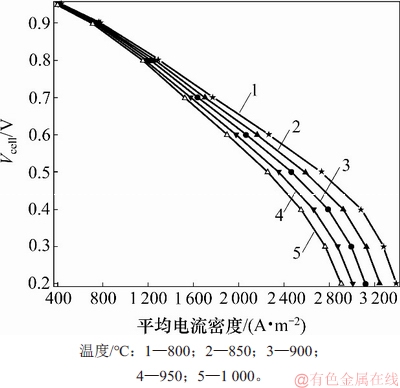
图9 不同温度下平均电流密度与工作电压的关系
Fig. 9 Relationship between average current density and working voltage at different temperatures
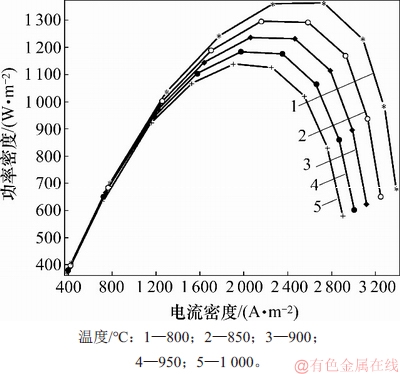
图10 不同温度下平均电流密度与功率密度的关系
Fig. 10 Relationship between average current density and power density at different temperatures
分析图9可知:在同一温度下,随着电流密度增大,电池工作电压不断下降。这是因为随着电流密度增大,电池极化现象越来越严重;当电流密度较低(800 A/m2以下)时,电池工作电压受温度的影响较小,而当电流密度较高时,电池工作电压受温度的影响很明显;温度越高,随着电流密度增大,电池工作电压越小,且下降速度越快。
随着温度升高,电池的活化极化、扩散极化和欧姆损失都会减少,固体电解质的离子导电率增大,气体扩散速度也会加快,电池电压反而会增高。在高温(800~1 000 ℃)下,离子电导率和扩散系数变化难以得到准确值,因而,模型将电解质的离子电导率和气体扩散系数简化为常数,不考虑温度升高对于传质的影响。据能斯特公式,处在标准状态的电池可逆电动势随温度升高而降低,比率为0.27 mV/℃[7]。模型验证了温度升高、电池工作电压降低的现象。
由图10可知:在模拟高温下(800~1 000 ℃),电流密度与功率密度呈抛物线型变化,表明在低电流密度时,功率密度的变化可以忽略;在同一平均电流密度下,随温度升高,电池的功率密度下降;当电流密度超过2 000 A/m2时,随温度升高,功率密度的极大值点反而朝电流密度减小的方向移动。
2.5 单电池长度对电池性能的影响
为研究不同长度时单电池内部气体分布情况以及电流密度分布情况,在温度为800 ℃,压力为1×105 Pa,极化值为0.5 V,燃料气体为40%氢气与60%水蒸气,阴极气体为15%氧气、37%水蒸气和58%氮气,其他参数按表1设置的条件下,计算氧气和氢气的质量分数分布情况,仿真结果分别如图11和图12所示。
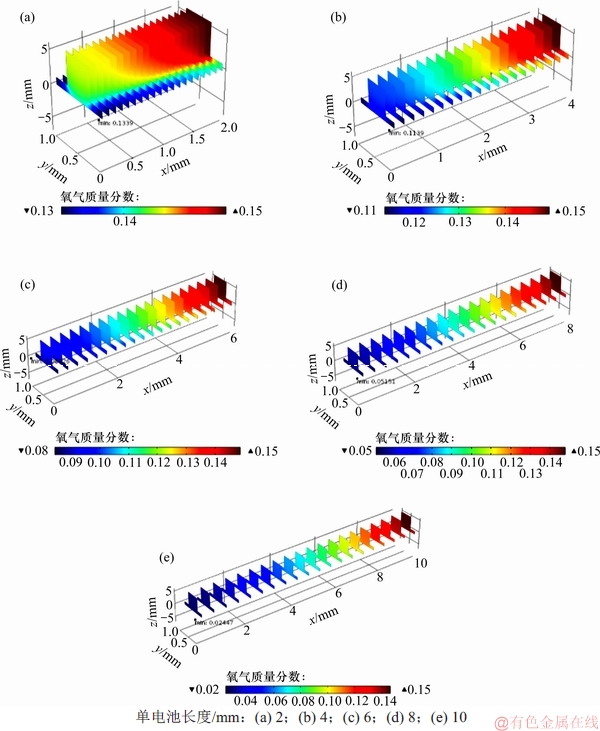
图11 氧气质量分数随单电池长度的变化
Fig. 11 Oxygen mass fraction varies with length of single cell
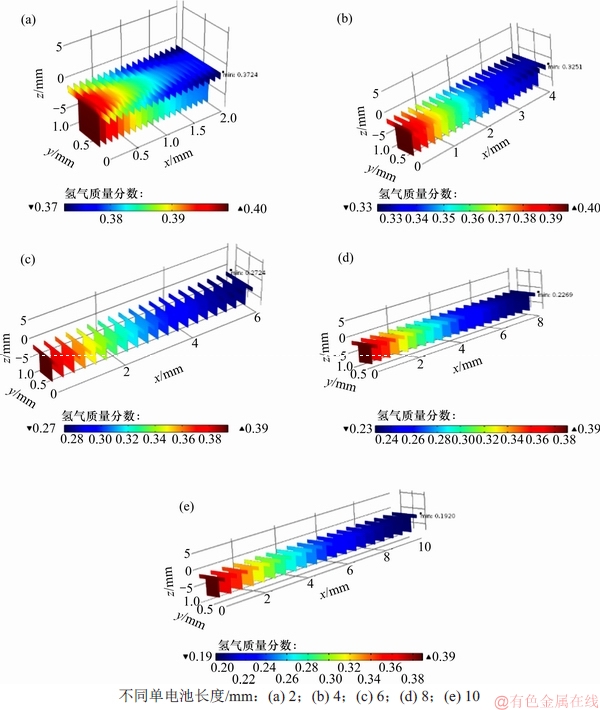
图12 氢气质量分数随单电池长度的变化
Fig. 12 Hydrogen mass fraction varies with length of single cell
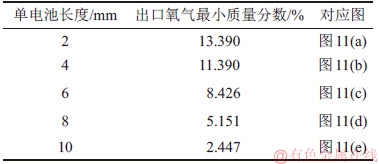
质量分数为15%的氧气从电池右端输入,左端流出,沿输入方向氧气被不断消耗。具体消耗情况如表4所示。
当单电池长度较短如2 mm时,氧气的消耗量很小,利用率不高;当长度为10 mm时,氧气消耗较充分。
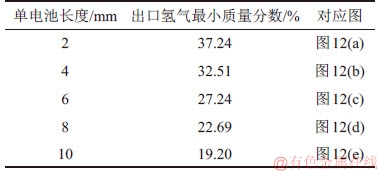
由图12可知:当电池长度改变时,氢气质量分数分布也会随之变化。质量分数为40%的氢气从电池右端输入,左端流出,沿输入方向氢气被不断消耗。具体消耗情况如表5所示。
因模型长度较短,氢气的利用率不高,电化学反应主要受氧气质量分数的影响。
表4 单电池长度对出口氧气质量分数的影响
Table 4 Effect of single cell length on oxygen mass fraction at outlet
在不同单电池长度下,平均电流密度与工作电压的关系见图13。从图13可知:
表5 单电池长度对出口氢气质量分数的影响
Table 5 Effect of single cell length on hydrogen mass fraction at outlet
1) 当单电池长度不变时,随着电流密度增大,电池工作电压不断下降。
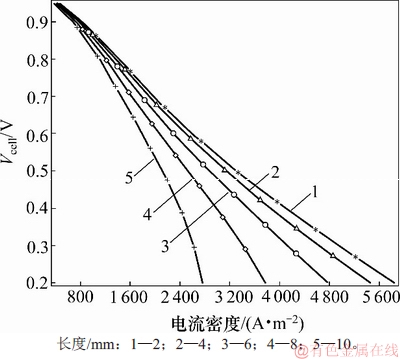
图13 不同单电池长度下平均电流密度与工作电压关系
Fig. 13 Relationship between average current density and working voltage under different single battery lengths
2) 单电池长度越长,随电流密度增大,电池工作电压下降速度越快。
3) 当电流密度较低(800 A/m2以下)时,电池工作电压受单电池长度的影响较小,而当电流密度较高时,电池工作电压受单电池长度的影响很明显。
4) 在同一较小电池电压下(小于0.5 V),随着单电池长度增加,电流密度下降速度增大。
3 结论
1) 入口处气体质量分数较大,电化学反应速率也较快,因此,气体入口处的质量分数变化往往比气体出口处质量分数的变化更快,优化气体流道设计对于提升电池性能有较大影响。
2) 在高电流密度下,入口氧气的质量分数会显著影响电池性能,而在低电流密度下,氧气质量分数不是影响电池电压的主要因素。
3) 当燃料气为氢气时,电池性能主要受氧气质量分数控制,平衡进气组分可以提高电池的燃料利用率,但同时也要考虑气体来源问题。当电池工作温度升高时,电池内部很多参数会发生变化,因此,要提升电池性能,必须从多个方面综合考虑。当单电池长度过小时,氧气的消耗量很小,利用率不高。
参考文献:
[1] 王吉华, 居钰生, 易正根, 等. 燃料电池技术发展及应用现状综述(上)[J]. 现代车用动力, 2018, 39(2): 7-12.
WANG Jihua, JU Yusheng, YI Zhenggen, et al. Review on development and application of fuel cell technology(1)[J]. Modern Vehicle Power, 2018, 39(2): 7-12.
[2] 王雅, 王傲. 中高温固体氧化物燃料电池发电系统发展现状及展望[J]. 船电技术, 2018, 38(7): 1-5.
WANG Ya, WANG Ao. Current status and perspective of intermediate-temperature solid oxide fuel cell[J]. Marine Electric & Electronic Engineering, 2018, 38(7): 1-5.
[3] 刘杨华. SOFC固体氧化物燃料电池分布式发电系统仿真及其潮流计算[D]. 长沙: 湖南大学电气与信息工程学院, 2010: 8-20.
LIU Yanghua. Research on distributed SOFC generation system simulation and power flower calculation[D]. Changsha: Hunan University. School of Electrical and Information Engineering, 2010: 8-20.
[4] 李忠收. 基于CFD的岸壁效应的数值模拟[D]. 大连: 大连海事大学航海学院, 2016: 7-22.
LI Zhongshou. Numerical simulation of wall effect based on CFD[D]. Dalian: Dalian Maritime University. Navigation College, 2016: 7-22.
[5] 罗新荣, 唐冠楚, 李亚伟, 等. CFD模型下采空区瓦斯抽采与注氮防灭火设计[J]. 中国安全科学学报, 2016, 26(6): 69-74.
LUO Xinrong, TANG Guanchu, LI Yawei, et al. Design of gas extraction and nitrogen injection fire control in goaf under CFD model[J]. Chinese Journal of Safety Science, 2016, 26(6): 69-74.
[6] 周铸, 黄江涛, 黄勇, 等. CFD技术在航空工程领域的应用、挑战与发展[J]. 航空学报, 2017, 38(3): 6-30.
ZHOU Zhu, HUANG Jiangtao, HUANG Yong, et al. Application, challenge and development of CFD technology in the field of aviation engineering[J]. Acta Aeronautics Sinica, 2017, 38(3): 6-30.
[7] WEI S S, WANG T H, WU J S. Numerical modeling of interconnect flow channel design and thermal stress analysis of a planar anode-supported solid oxide fuel cell stack[J]. Energy, 2014, 69: 553-561.
[8] MANGLIK R M, MAGAR Y N. Heat and mass transfer in planar anode-supported solid oxide fuel cells: effects of interconnect fuel/oxidant channel flow cross section[J]. Journal of Thermal Science and Engineering Applications, 2015, 7(4): 553-561.
[9] WANG K, HISSEL D, P RA M C, et al. A Review on solid oxide fuel cell models[J]. International Journal of Hydrogen Energy, 2011, 36(12): 7212-7228.
RA M C, et al. A Review on solid oxide fuel cell models[J]. International Journal of Hydrogen Energy, 2011, 36(12): 7212-7228.
[10] SORRENINO M, PIANESE C. Control oriented modeling of solid oxide fuel cell auxihary power unit for transportation application[J]. Journal of Fuel Cell Science and Technology, 2009, 6(4): 41011.
[11] BADWAL S P, BANNISTER M J, HANNINK R H J. Science and technology of zirconia V[M]. Lancaster, PA, USA: Technomic Pub Co, 1993: 540-546.
[12] UBERTINI S, BOVE R. Mathematical models:a general overview[C]//Modeling Solid Oxide Fuel Cells. Dordrecht, Netherlands: Springer, 2008: 51-93. DOI:10.1007/978-1-4020-6995-6_3.
[13] 蔡浩, 陈洁英, 邓奎, 等. 固体氧化物燃料电池系统及其应用[J]. 当代化工, 2014, 43(7): 1260-1261, 1264.
CAI Hao, CHEN Jieying, DENG Kui, et al. Solid oxide fuel cell system and its application[J]. Contemporary Chemical Industry, 2014, 43(7): 1260-1261, 1264.
[14] 曾淑琴. 固体氧化物燃料的电池电化学分析与数值仿真[D]. 武汉: 华中科技大学水电与数字化工程学院, 2007: 32-43.
ZENG Shuqin. Electrochemical analysis and numerical modeling of solid oxide fuel cell[D]. Wuhan: Huazhong University of Science and Technology. School of Hydropower and Digital Engineering, 2007: 32-43.
[15] 芮菊. 固体氧化物燃料电池(SOFC)的建模与仿真[D]. 上海: 上海交通大学信息与电气工程院, 2008: 39-68.
RUI Ju. The modeling and simulation for solid oxide fuel cell[D]. Shanghai: Shanghai Jiaotong University. School of Information and Electrical Engineering, 2008: 39-68.
[16] LI Jie, CHENG Yun, JIA Ming, et al. An electrochemical–thermal model based on dynamic responses for lithium iron phosphate battery[J]. Journal of Power Sources, 2014, 255: 130-143.
[17] TANG Yiwei, JIA Ming, AI Lihua, et al. Capacity fade analysis of the lithium-ion power battery cycling process based on an electrochemical-thermal coupling model[J]. Energy Technology, 2015, 3(12): 1250-1259.
[18] FARMANN A, WAAG W, SAUER D U. Application-specific electrical characterization of high power batteries with lithium titanate anodes for electric vehicles[J]. Energy, 2016, 112: 294-306.
[19] MEHLAWAT M K, KUMAR A, YADAV S, et al. Data envelopment analysis based fuzzy multi-objective portfolio selection model involving higher moments[J]. Information Sciences, 2018, 460/461: 128-150.
[20] ILBAS M, KUMUK B. Numerical modelling of a cathode-supported solid oxide fuel cell (SOFC) in comparison with an electrolyte-supported model[J]. Journal of the Energy Institute, 2019, 92(3): 682-692.
(编辑 陈灿华)
收稿日期: 2019 -02 -22; 修回日期: 2019 -04 -25
基金项目(Foundation item):国家重点研发计划项目(2018YFB0104200);国家自然科学基金资助项目(51774343)(Project (2018YFB0104200) supported by the National Key R & D Program of China; Project(51774343) supported by the National Natural Science Foundation of China)
通信作者:贾明,博士,副教授,从事电化学储能器件及系统的多尺度多物理场仿真、固态储电器件制造研究;E-mail:jiamingsunmoon@aliyun.com