J. Cent. South Univ. Technol. (2010) 17: 1133-1138

DOI: 10.1007/s11771-010-0608-z

Impedance spectroscopy study on Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites

KUMAR S¹, BATOO K M², PRAKASH R³, CHOI H K¹, KOO B H¹, SONG J I³,

CHUNG H⁴, JEONG H⁴, LEE C G¹

1. School of Nano and Advanced Materials Engineering, Changwon National University,

Changwon 641-773, Korea;

2. King Abdullah Institute for Nanotechnology, King Saud University, Riyadh 11451, Saudi Arabia;

3. Department of Mechanical Engineering, Changwon National University, Changwon 641-773, Korea;

4. Department of Precision & Mechanical Engineering and BK21 Eco-Friendly Heat & Cold Energy Mechanical Research Team, Gyeongsang National University, Tongyeong 650-160, Korea

? Central South University Press and Springer-Verlag Berlin Heidelberg 2010

Abstract: The complex impedance spectroscopy and surface morphology of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) system, prepared using a conventional solid state reaction technique, were investigated. The impedance spectroscopy measurements were carried out at room temperature in the frequency range of 42-5 MHz. The electrical processes in the samples were modeled in the form of an equivalent circuit made up of a combination of two parallel RC circuits attributed to grain and grain boundaries. The DC conductivity obtained by extrapolation of AC data using impedance spectroscopy and four-probe method increases at 10% doping of Ti ions. The energy-dispersive X-ray (EDX) pattern confirmed the homogeneous mixing of the Mn, Fe, Ti and O atoms in pure and doped ferrite samples.

Key words: spinel ferrite; magnetic properties; impedance spectroscopy; Ti⁴⁺ ions; doping

1 Introduction

Ferrites as semiconductors have attracted considerable attention in the field of technological application in a wide range of frequencies extending from microwave to radio frequency [1]. However, there has been a growing interest in study of magnetic, electric and structural properties of mixed spinel ferrite [2-7]. The basis for the wide range of applications is related to the variety of transition metal cations that can be incorporated into the lattice of the parent magnetic structure. The physical properties of spinel ferrites, such as transition temperature and saturation magnetic moment, are strongly dependent on the distribution of cations and type of doping atom. Impedance spectroscopy has emerged over the past several years as a powerful technique for the electrical characterization of electrochemical systems. The strength of the method lies in the fact that by small-signal perturbation it reveals both the relaxation time and relaxation amplitudes of various processes present in a dynamic system over a wide range of frequency [8]. The electrical properties of polycrystalline materials are generally determined by this technique with AC frequencies typically in the range between 10⁶ and 10^-1 Hz [9]. Many research groups studied the effect of the substitution of Ti⁴⁺ ions on the magnetic, electric and dielectric properties of ferrite [10-14]. BRAND et al [11] found (in case of Mg_1+xTi_xFe_2-2xO₄) that at higher concentrations of Ti, system approaches towards the spin-glass, whereas DORMANN et al [7] reported canted spin arrangement in the magnetization study of Ti⁴⁺ substituted lithium ferrite. However, some of the groups have reported that the substitution of Ti⁴⁺ ions reduces the electrical conductivity, dielectric constant and dielectric loss [13-14]. KUMAR et al [15] reported the increase in the electrical conductivity in Mg-Mn ferrites with 20% of Ti doping.

2 Experimental

The spinel ferrite samples of Mn_1+xFe_2-2xTi_xO₄ (0≤ x≤0.5) were prepared using a conventional solid-state reaction technique. The stoichiometric amount of highly pure powders of MnO₂, Fe₂O₃ and TiO₂ were mixed thoroughly and pre-calcinated at 1 000 ℃ for 12 h. The pre-calcinated materials were again ground and calcinated at 1 250 ℃ for 24 h. Finally, the samples were ground to very fine powder, pressed into pellet form and sintered at 1 300 ℃ for 24 h, and then cooled slowly to room temperature. The pressed samples were coated on adjacent faces with silver paste, thereby forming parallel plate capacitor geometry. The impedance measurements were made from 42 Hz up to 5 MHZ using LCR HI-Tester (HIOKI 3532-50). The DC conductivity of the samples was measured using a Keithley electrometer (Model 617) in the temperature range from 200 to 400 K. The temperature was controlled with an accuracy of   0.05 K using Lakeshore (Model 340) temperature controller.

3 Results and discussion

Impedance spectroscopy is an ideal tool for investigating the electrical response of dielectric materials as a function of frequency. It can be used to study the impedance behavior of a material and can be analyzed based on an idealized circuit model with discrete electrical components. The analysis is mainly accomplished by fitting the impedance data to an equivalent circuit, which is representative of the material under investigation. A widely used frequency dependent complex dielectric function is represented by:

                        (1)

where ε^*(ω) is the permittivity; and ω is the frequency.

The complex impedance technique is used to separate the grain and grain boundary to study their microstructures associated with the grain and grain boundaries. The Cole-Cole plot or Nyquist plot is particularly useful for the materials that possess one or more well separated relaxation processes with comparable magnitudes and obey the Debye or Cole-Cole functional forms. The measurements of impedance give us information about the resistive (real part, superscript “′”) and reactive (imaginary part, superscript “″”) components in a material. This plot can be drawn for any five complex parameters such as: permittivity (ε^*), impedance (Z^*), admittance (Y^*), electric modulus (M^*) and dielectric loss tangent (tan δ). These parameters are related with each other as follows [16]:

tan δ=ε″/ε′=M″/M′=Z′/Z″=Y′/Y″                   (2)

The plot can give two semi-circles, depending upon the electrical properties of the material. The first semicircle in a low frequency domain represents the resistance of grain boundary. The second one obtained in a high frequency domain corresponds to the resistance of grain or bulk properties. The relationship between resistive part (Z′) and the reactive part (Z″) is used to distinguish contributions between the grain and grain boundary for various compositions of x as shown in Fig.1.

The complex impedance can be calculated from the relationship:

Z^*(ω)=Z′(ω)-iZ″(ω), i=1                       (3)

where Z′ and Z″ are respectively real and imaginary parts of impedance and can be written as

               (4)

               (5)

where R_g, R_gb, C_g and C_gb represent resistances and capacitances of grain and grain boundary, respectively. The resistances are calculated from the circular arc intercepts on Z′-axis, while the capacitances are derived from the height of the circular arcs. The maximum height in each semicircle is

Z_real(ω)τ₀ω=-Z″(ω)                            (6)

where τ is the relaxation time.

Hence, using this condition and with the help of the above equations, the relaxation time can be calculated for the grain and grain boundary by using the following relationship:

τ_g=1/ω_g=R_gC_g                                (7)

τ_gb=1/ω_gb=R_gbC_gb                              (8)

The Nyquist diagrams obtained from Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) at room temperature are displayed in Fig.1. It can be seen that all samples comprise two semicircles arcs with their centers lying below the real axis. The high-frequency semicircle can be attributed to the grain property of the materials, while the other semicircular arc appears in the low frequency domain of the impedance spectrum due to the presence of grain boundaries. Two semicircles arcs of the impedance can be expressed as an equivalent circuit consisting of parallel combination of two resistances and capacitance connected in series. Both the grain interior and the grain boundary have different resistances and can be evaluated from the impedance spectrum by its circular fitting using Z-plot computer program. The data fitted are shown in the insets of Fig.1. The resistances for grain and grain boundary (R_g and R_gb) and capacitances (C_g and C_gb) are calculated and shown in the inset of Fig.1. It is evident that the grain boundary resistances are larger than those of the grain. This is ascribed to the fact that the atomic arrangement near the grain boundary region is disordered due to the increase in electron scattering. The higher boundary resistance also arises from other factors such as the decrease in Fe²⁺ ion content in the region. The capacitance of grain boundary is much larger than that of the grain because the capacitances are inversely proportional to the thickness of the media. The DC conductivity estimated from the AC data using impedance spectroscopy is plotted in Fig.2. From Fig.2, it is observed that DC conductivity is found to decrease with increasing Ti⁴⁺ ion content except for the sample with x=0.1, which means that when x is more than 0.1, the addition of Ti⁴⁺ ions in the samples helps to form aggregates on the grain boundary, which impedes the conduction process and decreases the dielectric polarization and conductivity of the samples. It is expected that the conduction process occurs as a result of electron exchange between Fe²⁺ and Fe³⁺ ions and hole transfer between Mn²⁺ and Mn³⁺ ions at the octahedral (A) site. It is suggested that Ti⁴⁺ ions will occupy A-site when they are added in a small amount (x is less than 0.2); with further increase of Ti⁴⁺ ion content, it will occupy the B-site [16]. The presence of Ti⁴⁺ ions at B-site when x is more than 0.1 will act as electrostatic trap for the electron exchange between Fe²⁺ and Fe³⁺ ions by forming electrostatic bonds with Fe²⁺ ions [16]. At the same time, the replacement of Fe²⁺ and Fe³⁺ ions by Ti⁴⁺ ions will reduce the concentrations of both Fe²⁺ and Fe³⁺ ions in B-site. So, the overall effect of the addition of Ti⁴⁺ ions in the system is expected to reduce the electrical conductivity and polarization.

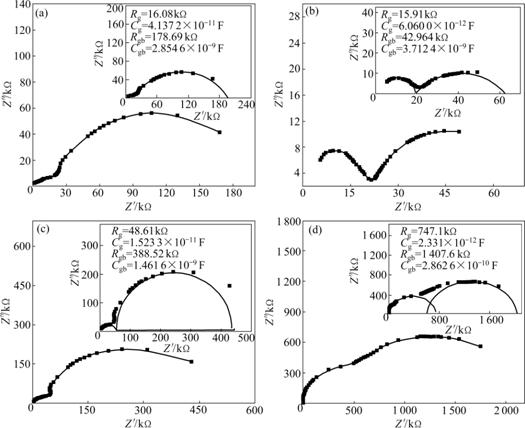
Fig.1 Nyquist plots for Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites with different x values at room temperatures (Insets show fitted impedance spectra and calculated values of grain and grain boundary resistance (R_g, R_gb) and capacitances (C_g, C_gb) of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5): (a) x=0; (b) x=0.1; (c) x=0.3; (d) x=0.5

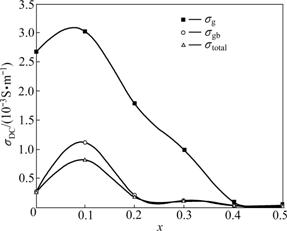
Fig.2 DC conductivity versus Ti⁴⁺ ion content at room temperature

The effect of temperature on DC electrical conductivity of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites investigated from 200 to 400 K is shown in Fig.3. The electrical conductivity σ increases with increasing temperature T. This can be attributed to the increase in the drift mobility of electric charge carriers, which are

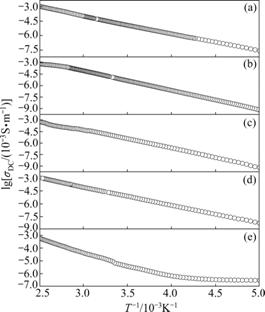
Fig.3 DC conductivity as function of temperature for Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites: (a) x=0; (b) x=0.1; (c) x= 0.2; (d) x=0.3; (e) x=0.5

Table 1 Electrical parameters of Mn_1+xFe_2-2xTi_xO₄ ferrites (0≤x≤0.5) at room temperature

In order to understand the morphology, grain size and shape of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) samples, SEM study was carried out. The SEM images were taken for different parts of the samples. The SEM images of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) samples are shown in Fig.4. It is clearly seen from the SEM images that the microstructure is changed with the doping of Ti⁴⁺ ions. With the substitution of Ti⁴⁺ ion, the numbers of pores are reduced as the grains are closer to each other and the effective area of grain contact increases. This, in turn, results in greater densification or less porosity. The chemical compositions of samples of different compositions were calculated from EDX. Fig.5 shows the typical EDX pattern for various compositions of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) samples. The EDX patterns confirm the homogeneous mixing of Mn, Fe, Ti and O atoms in pure and doped ferrite samples. The observed composition is almost equal to that of the sample produced by stoichiometric calculations while taking oxygen as balanced. The results of the composition obtained from EDX analysis for Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) samples are shown in the inset of Fig.5.

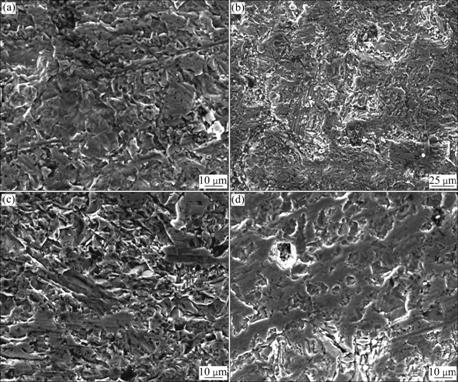
Fig.4 SEM images of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites: (a) x=0; (b) x=0.1; (c) x=0.3; (d) x=0.5

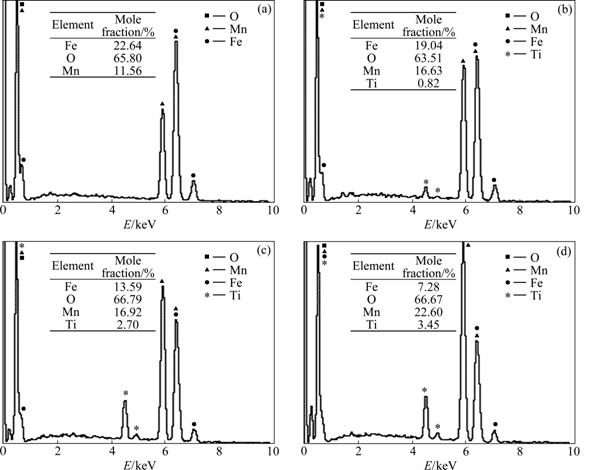
Fig.5 EDX results of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) ferrites (Insets show composition of Mn_1+xFe_2-2xTi_xO₄ (0≤x≤0.5) samples):   (a) x=0; (b) x=0.1; (c) x=0.3; (d) x=0.5

4 Conclusions

(1) Electrical properties of Mn_1+xFe_2-2xTi_xO₄ (0≤  x≤0.5) ferrites are studied by a complex impedance spectroscopy technique.

(2) The complex impedance results provide convincing evidence for the existence of both the grain and grain boundary effects in the studied samples.

(3) The activation energy calculated from DC conductivity is found to have minimum value at 10% doping of Ti⁴⁺ ions, which is consistent with the DC conductivity calculated from the impedance study.

(4) The chemical composition measured by EDX shows that Fe ions are replaced by Ti and Mn ions in the system. SEM results infer that doping of Ti⁴⁺ ions reduces the porosity and results in densification in the system.

References

[1] DIAS A, MOREIRA R L. Conductivity behavior of n-type semiconducting ferrites from hydrothermal powders [J]. Journal of Materials Research, 1998, 13(8): 2190-2194.

[2] KUMAR S, KUMAR R, DOGRA A, REDDY V R, BANERJEE A, ALIMUDDIN. Multiferroic behavior of Ti doped Mn_0.95Mn_0.05Fe₂O₄ [J]. Indian Journal of Pure and Applied Physics, 2007, 45(1): 31-36.

[3] BHARGAVA S C, ZEMAN N. M?ssbauer study of Ni_0.25Zn_0.75Fe₂O₄. I: Spin fluctuations [J]. Physical Review B, 1980, 21(5): 1717-1725.

[4] MURALIDHARAN K, SRIVASTAVA J K, MARATHE V R, VIJAVARAGHAVAN R. On the magnetic ordering in the disordered spinels Zn_xCo_1-xFeCrO₄ [J]. Journal of Physics C: Solid State Physics, 1985, 18(31): 5897-5908.

[5] BRAND R A, LAUER J, HERLACH D M. The evaluation of hyperfine field distributions in overlapping and asymmetric Mossbauer spectra: A study of the amorphous alloy Pd_77.5-xCu₆Si_16.5Fe_x [J]. Journal of Physics F: Metal Physics, 1983, 13(3): 675-684.

[6] DORMANN J M, NOGUES M. Magnetic structures in substituted ferrites [J]. Journal of Physics: Condensed Matter, 1990, 2(5): 1223- 1238.

[7] DORMANN J L, HARFAUNI M EI, NOGUES M, JOVE J. Relaxation of the transverse spin component in randomly canted Li-Ti ferrite below T_N [J]. Journal of Physics C: Solid State Physics, 1987, 20(10): 161-166.

[8] MACDONALD J R. Impedance spectroscopy [M]. New York: John Wiley, 1987: 12-28.

[9] BOUCHET R, KNAUTH P, LAUGIER J M. Theoretical analysis of the impedance spectra of electroceramics (Part 2): Isotropic grain boundaries [J]. Journal of Electroceramic, 2006, 16(3): 229-238.

[10] KUMAR S, ALIMUDDIN S, KUMAR R, DOGRA A, REDDY V R, BANERJEE A. M?ssbauer and magnetic studies of multiferroic Mg_0.95Mn_0.05Fe_2-2xTi_2xO₄ system [J]. Journal of Applied Physics, 2006, 99: 08M910.

[11] BRAND R A, GEORGES-GIBERT H, HUBSCH J, HELLER I A. Ferrimagnetic to spin glass transition in the mixed spinel Mg_1+tFe_2-2tTi_tO₄: A Mossbauer and DC susceptibility study [J]. Journal of Physics F: Metal Physics, 1987, 15(9): 1987-2008.

[12] SURYAVANSHI S S, PATIL R S, PATIL S A, SAWANT S R. DC conductivity and dielectric behavior of Ti⁴⁺ substituted Mg-Zn ferrites [J]. Journal of the Less Common Metals, 1991, 168(2): 169-174.

[13] REDDY M B, REDDY V. Electrical conductivity of some mixed Li-Ti ferrites [J]. Physica Status Solidi, 2006, 220(2): 575-580.

[14] CHANDRA P, BAIJAL J S. Dielectric behaviour of tetravalent titanium-substituted Ni-Zn ferrites [J]. Journal of the Less Common Metals, 1985, 107(1): 51-57.

[15] KUMAR S, ALIMUDDIN, KUMAR R, THAKUR P, CHAE K H, ANGADI B, CHOI W K. Electrical transport, magnetic, and electronic structure studies of Mg_0.95Mn_0.05Fe_2-2xTi_2xO_4±δ (0≤x≤0.5) ferrites [J]. Journal of Physics: Condensed Matter, 2007, 19(47): 476210.

[16] DUTTA S, CHOUDHARY R N P, SINHA P K. Impedance spectroscopy studies on Ga-ion-modified PLZT ceramics [J]. Physica Status Solidi, 2005, 202(6): 1172-1181.

(Edited by CHEN Wei-ping)

Corresponding author: KUMAR S, PhD, Research Professor; Tel: +82-55-2133701; E-mail: shailuphy@gmail.com