J. Cent. South Univ. Technol. (2008) 15: 361-367

DOI: 10.1007/s11771-008-0068-x

Numerical simulation for explosion wave propagation of combustible mixture gas

WANG Cheng(王 成), NING Jian-guo(宁建国), MA Tian-bao(马天宝)

(State Key Laboratory of Explosion Science and Technology, Beijing Institute of Technology,

Beijing 100081, China)

Abstract: A two-dimensional multi-material code was indigenously developed to investigate the effects of duct boundary conditions and ignition positions on the propagation law of explosion wave for hydrogen and methane-based combustible mixture gas. In the code, Young’s technique was employed to track the interface between the explosion products and air, and combustible function model was adopted to simulate ignition process. The code was employed to study explosion flow field inside and outside the duct and to obtain peak pressures in different boundary conditions and ignition positions. Numerical results suggest that during the propagation in a duct, for point initiation, the curvature of spherical wave front gradually decreases and evolves into plane wave. Due to the multiple reflections on the duct wall, multi-peak values appear on pressure—time curve, and peak pressure strongly relies on the duct boundary conditions and ignition position. When explosive wave reaches the exit of the duct, explosion products expand outward and forms shock wave in air. Multiple rarefaction waves also occur and propagate upstream along the duct to decrease the pressure in the duct. The results are in agreement with one-dimensional isentropic gas flow theory of the explosion products, and indicate that the ignition model and multi-material interface treatment method are feasible.

Key words: combustible mixture gas; explosion wave; interface treatment; combustion function mode

1 Introduction

In mining and other related industries, explosion related accidents occur frequently, the main cause is the combustible gases^[1-2]. These occurrences normally attribute to leakage of combustible mixture gas in the mining or industrial ducts. When mixed with air, such gases react violently. If ignited by some initiation sources, they form a turbulent flow, and become combustible, explosive and even detonable due to disturbance from barriers such as equipment and ducts^[3-8]. It is, therefore, of great significance to conduct research on propagation process of explosive wave produced by combustible mixture gas after ignition. This resembles an explosion of a non-ideal explosive. In contrast to explosion of condensed explosives, such a gas explosion is characterized by slowering pressure-rise, longer energy release time and longer over-pressure acting time on structures^[9-10]. Due to this fact and unavailability of analytical solutions for the explosive wave produced by combustible mixture gas, the research on explosion of combustible mixture gas was mainly carried out by numerical simulation. In recent years, ORAN et al^[11] numerically have simulated the cellular detonation of H₂-O₂-Ar mixture gas. Their results indicated that the collision of triple wave points plays a very important role in the secondary initiation. With the combination of a front tracking method with a Godunov-type solver for the Euler equations, BIELERT and SICHE^[12] investigated the propagation process of detonation of ethylene/oxygen and methane/air mixtures at different mixing ratios in the duct. WANG and XU^[13] used five-order WENO scheme and elementary reaction model to simulate the propagation process of the detonation wave for H₂-O₂ mixture gas in heart-shaped duct, and analyzed the process of wave system evolution and chemical dynamics accompanying the secondary initiation. ZHANG et al^[14] adopted simplified two-stage chemical reaction model and improved high precision space-time conservation method (CE/SE) to simulate deflagration-to-detonation process of combustible gas. All these previous numerical simulation studies were performed using single gas and only one material in calculation domain. Up to our knowledge, there is no substantial understanding on the explosion characteristics of combustible mixture gas and two or more materials in calculation domain. The need therefore arises to study such situations. With our indigenously developed two-dimensional Euler code based on Young’s technique for processing multi-material interface and combustion function model to simulate ignition process, numerical analyses were performed for the evolution process of the explosive flow field inside and outside the duct when hydrogen and methane-based combustible mixture gas exploded in the duct. Based on simulations, various effects were postulated depending on various combinations of boundary and ignition conditions.

2 Numerical calculation model

The explosion process of combustible mixture gas was described by two-dimensional non-steady hydrodynamics equation group. Basic equations with Euler coordinates are as follows^[15-17].

Mass conservation equation:

       (1)

Momentum conservation equation:

              (2)

               (3)

Energy conservation equation:

      (4)

where  t represents time; r and z represent the Euler coordinate; u_r and u_z  represent velocity component along directions r and z, respectively; p, ρ and e represent pressure, density and specific internal energy, respectively.

Ideal gas equation of state was used for both combustible gas mixture and air:

p=(γ-1)ρe                                   (5)

3 Calculation of explosion wave

The explosion process of combustible gas mixture is characterized by a longer explosion time. Therefore, it is evident that instantaneous detonation model cannot be applied to such situations. For this, a combustion function F ranging from 0 to 1 was introduced in the program, which allowed the energy to be released according to a given mechanism. A chemical reaction rate was also introduced and the material in the transition area was treated as a kind of incomplete explosive products. Simulation of propagation of explosion wave by such model was enough to meet requirements^[1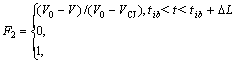8].

          (8)

where   represents the initial energy of wave front, Q is the chemical energy; ?L=r_b(?z²+?r²)^1/2/D_CJ, r_b is adjustable parameter; t_ib is the initiation time for the ith line cells; V₀ is the initial specific volume of combustible mixture gas; V_CJ is the specific volume of mixture gas C-J; D_CJ is the detonation velocity of mixture gas C-J.

4 Numerical computation method

The ‘operator split’ differential scheme was adopted in calculation. For each direction, the calculations of the governing equations consist of two steps. The first step was a pressure effect step (Lagrange step), in which only gradient effects of pressure and deviatoric stress were considered and convection terms were ignored. In this step, the intermediate values of cell velocity and specific internal energy were obtained. The second step was Euler step, in which mass, momentum and energy were redistributed within cells, by which new cell velocity and mass and internal energy of each material within cells were obtained^[15]. For this step, one-dimensional transport algorithm was used. Alternative transport was made in directions r and z to ensure the stability of the scheme. In calculation, artificial viscosity was used to capture shock wave. Time step was determined by the stability of CFL (Courant-Friedrichs-Lewy). The interface between explosive products and air was tracked by Young’s interface reconstruction technique. Its basic idea is to approximate the material interface in mixed cells by a straight line. The volume fractions of materials in eight cells around were employed to determine the normal direction of the straight line, and the volume fractions of mixed cells were used to determine the location of the straight line^[19]. Fig.1 demonstrates the location of the material interface in mixed cell Ω(i, j) with a line segment.

Supposing that φ is the volume fraction of material C in the mixed cells, and φ_E, φ_W, φ_N and φ_S are the

Fig.1 Distribution diagram of cells

volume fractions of material C on the four sides of the cell, there exist

             (9)

where  α is a adjustment coefficient, α=2.

Interface slope k was defined as

                               (10)

                            (11)

Then the position of the interface was adjusted so that it divided the cell into two parts that matched the actual volume fractions of two materials in the cell.

5 Numerical simulation of explosion of com- bustible mixture gas

5.1 Numerical simulation of explosion of combustible gas mixture in duct

Considering various types of industrial ducts^[2,20], five cases shown in Fig.2 were taken up in the work. Due to axis-symmetric nature, only one half of the duct was needed to be considered in calculation. The five cases were: (a) closed left end, open right end, initiation point at the right end; (b) closed left end, open right end, initiation point at the left end; (c) both ends closed, initiation point at the left end; (d) both ends open, initiation point at the left end; (e) a cylindrical vessel, initiation point at the center of the vessel. The ducts in

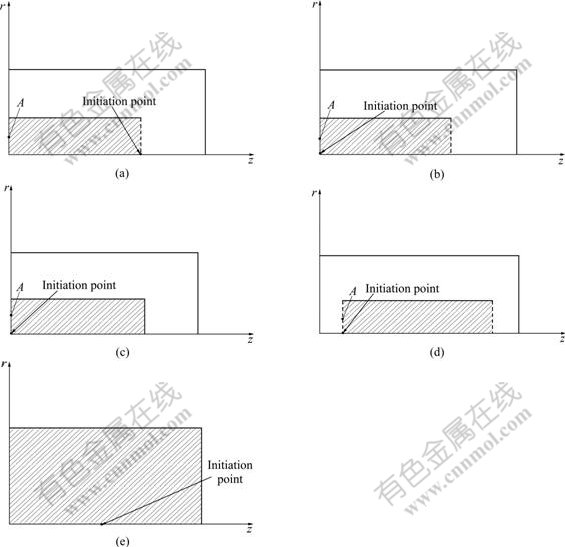
Fig.2 Schemes of initial field for five cases: (a) Closed left end, open right end, initiation point at right end; (b) Closed left end, open right end, initiation point at left end; (c) Both ends closed, initiation point at left end; (d) Both ends open, initiation point at left end;  (e) A cylindrical vessel, initiation point at center of vessel

the first four cases (Figs.2(a)-(d)) were 12 m in length and 4 m in diameter. For case five (Fig.2(e)), the ratio of height to diameter for the cylindrical vessel was 1.

5.2 Discussion of numerical results

Main components of combustible mixture gas in calculation are listed in Table 1. The stoichiometric concentration for the combustible mixture gas was 19.2%. If mixed with air according to the stoichiometric concentration, the density was 1.19 mg/cm³. In calculation, the wall of the vessel was considered rigid while gas-solid coupling was neglected.

Table 1 Components of combustible mixture gas (volume fraction, %)

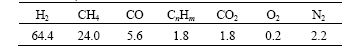
C_nH_m is mainly unsaturated hydrocarbon.

Figs.3-7 illustrate the wave structure and its evolution process of the explosion field of combustible mixture gas in the ducts at different times, and N is calculation step. The pressure—time curves at point A for different cases are shown in Fig.8. It can be seen from Figs.3-6 that, when propagating forward, the spherical wave from initiation point suffers multiple reflections at the wall of the ducts, thus producing complicated flow field. Since the wave surface curvature gradually decreases, the spherical wave turns into plane wave after traversing a certain distance. For ducts with open end, when explosion wave propagates to the exit of the ducts, explosive products expand outward and form shock wave in air. In the meantime, rarefaction wave occurring propagates into the ducts, thus decreasing the pressure in the ducts. For case in Fig.7, it can be observed that the spherical wave formed by initiation point causes regular reflection on the top and the sides of the cylindrical vessel. After interacting with each other, reflected shock waves continue to propagate along their respective original directions. As time advances, these reflected waves are reflected for many times on the top and sides, which produce fairly complex wave system structure.

For ducts with a closed left end and an open right end, the pressure—time curves at point A for initiation at the open right end and the closed left end are shown in Figs.8(a) and (b), respectively. In case of ignition point at the open right end, at t=18.20 ms, the pressure at point A reaches a peak value of 4.00 MPa and thereafter decreases rapidly, in accordance with the results deduced from one-dimension isentropic flow of explosive products^[18]; in case of ignition point at the closed left end, at t=0.64 ms, the pressure at point A reaches a peak value of 1.32 MPa. Thus, the pressure produced for initiation at the open right end is twice as high as that produced for initiation at the closed left end. In the two cases, the pressure on rigid wall is different, but the impulse is equal. Fig.8(c) represents the pressure—time curve at point A in the case of two closed ends. At t=0.39 ms, the peak pressure at point A reaches a peak value of 1.16 MPa. After that time, the pressure drops to 1.00 MPa and almost maintains this value till t=34.90 ms. After that, due to the reflected shock wave from the other end, the pressure increases. Fig.8(d) represents the pressure—time curve at point A for two open ends. At t=0.39 ms, the pressure of point A reaches a peak value of 1.17 MPa. Pressure then rapidly drops due to the rarefaction wave.

Multi-peak values appearing in Figs.8(b)-(d) are caused by reflection on the sidewall. However, the phenomenon does not occur in Fig.8(a), which can be

Fig.3 Explosion wave propagation process of combustible mixture gas in ducts (Duct with a closed left end and an open right end, initiation point at open right end): (a) N=1 000; (b) N=3 000; (c) N=5 000; (d) N=7 000; (e) N=9 000; (f) N=10 000

Fig.4 Explosion wave propagation process of combustible mixture gas in ducts (Duct with a closed left end and an open right end, initiation point at closed left end): (a) N=1 000; (b) N=3 000; (c) N=5 000; (d) N=7 000; (e) N=9 000; (f) N=10 000

Fig.5 Explosion wave propagation process of combustible mixture gas in ducts (Duct with two closed ends, initiation point at closed left end): (a) N=1 000; (b) N=3 000; (c) N=5 000; (d) N=7 000; (e) N=9 000; (f) N=10 000

Fig.6 Explosion wave propagation process of combustible mixture gas in ducts (Duct with two open ends, initiation point at open left end): (a) N=1 000; (b) N=3 000; (c) N=5 000; (d) N=7 000; (e) N=9 000; (f) N=10 000

Fig.7 Explosion wave propagation process of combustible mixture gas in cylindrical vessel: (a) N=1 000; (b) N=3 000; (c) N=5 000; (d) N=7 000; (e) N=9 000; (f) N=10 000

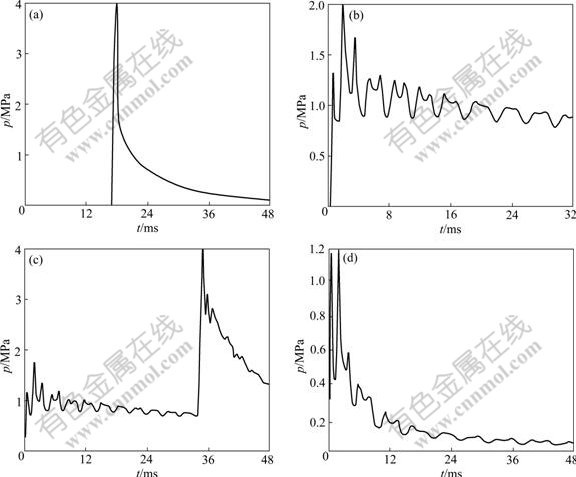
Fig.8 Pressure—time curves at point A: (a) Duct with closed left end and an open right end, initiation point at open right end; (b) Duct with closed left end and an open right end, initiation point at closed left end; (c) Duct with two closed ends, initiation point at closed left end; (d) Duct with two open ends, initiation point at open left end

explained by the fact that explosion wave has gradually turned into plane wave, and it is not reflected on the sidewall^[21-22].

6 Conclusions

1) Using indigenously developed 2D Euler code, numerical simulations are performed for the propagation of the explosion wave produced by hydrogen and methane-based combustible mixture gas inside and outside the ducts under five different boundary conditions and the ignition positions. In the code, Young’s technique is employed to track the multi-material interface and combustion function model is adopted to simulate ignition process. The calculation results are largely in agreement with one-dimensional isentropic gas flow theory of the explosion products, which indicates the validity of multi-material interface treatment technique and ignition model used.

2) By comparing the peak pressure curves at the ends of the duct, it is found that different boundary conditions and ignition positions have strong influence on peak pressure, wave shape and propagation process of explosive waves inside and outside the duct. For a duct with one open end and one closed end, the pressure at closed end for initiation point at open end is twice as high as that at closed end. Thus, these factors should be taken into account when a duct transporting combustible mixture gas is designed and protected.

3) The peak pressure of explosion of hydrogen and methane-based mixture gas is lower than that of condensed explosives. However, due to its longer positive phase pressure and large momentum, the lethality of such explosions is comparable to condensed explosives. Thus, with such numerical procedures, awareness for preventing combustible gas explosions can be enhanced among working personnel to minimize and even eliminate occurrence of accidents.

References

[1] LIN Bai-quan, ZHANG Ren-gui, L? Heng-hong. Research on acceleration mechanism and flame transmission in gas explosion [J]. Journal of China Coal Society, 1999, 24(1): 164-167. (in Chinese)

[2] LU Jie, NING Jian-guo, WANG Cheng, LIN Bai-quan. Study on flame propagation and acceleration mechanism of city coal gas [J]. Explosion and Shock Waves, 2004, 24(4), 305-311. (in Chinese)

[3] VAAGSAETHER K, KNUDSEN V, BJERKETVEDT D. Simulation of flame acceleration and DDT in H₂-air mixture with a flux limiter centered method [J]. International Journal of Hydrogen Energy, 2007, 32(13): 2186-2191.

[4] ORAN E S, GAMEZO V N. Origins of the deflagration-to- detonation transition in gas-phase combustion [J]. Combustion and Flame, 2007, 148(1/2): 4-47.

[5] FAIRWEATHER M, HARGRAVE G K, IBRAHIM S S. Studies of premixed flame propagation in explosion tubes [J]. Combustion and Flame, 1999, 116(4): 504-518.

[6] DUNN R D, MCCANN M A. Overpressure from nondetonating baffle-accelerated turbulent flame in tubes [J]. Combustion and Flame, 2000, 120(4): 504-514.

[7] GAMEZO V N, OGAWA T, ORAN E S. Numerical simulations of flame propagation and DDT in obstructed channels filled with hydrogen-air mixture [C]// Proceedings of the Combustion Institute 2007, 31(2): 2463-2471.

[8] NAAMANSEN P, BARALDI D, HJERTAGER B H, SOLBERG T, CANT S. Solution adaptive CFD simulation of premixed flame propagation over various solid obstructions [J]. Journal of Loss Prevention in the Process Industries, 2002, 15(3): 189-197.

[9] NING Jian-guo WANG Cheng, LU Jie. Explosion characteristics of coal gas under various initial temperatures and pressures [J]. Shock Waves, 2006, 15(6): 461-472.

[10] WANG Cheng, NING Jian-guo, LEI Juan. Numerical study on propagation of explosion wave in H₂-O₂ mixtures [J]. Lecture Notes in Computer Science, 2006, 4222: 816-819.

[11] ORAN E S, WEBER J E, STEFANIW E I, LEFEBVRE M H, ANDERSON J D. A numerical study of two-dimensional H₂-O₂-Ar detonation using a detailed chemical reaction model [J]. Combustion and Flame, 1998, 113(1/2): 147-163.

[12] BIELERT U, SICHE M. Numerical simulation of premixed combustion processes in closed tubes [J]. Combustion and Flame, 1998, 114(3/4): 397-419.

[13] WANG Chang-jian, XU Sheng-li. Numerical study on re-initiation phenomenon of gaseous detonation induced by the coalescence of high temperature regions [J]. Acta Aerodynamica Sinica, 2007, 25(1): 70-75. (in Chinese)

[14] ZHANG De-liang, XIE Wei, GUO Chang-ming, HU Xiang-yu. Numerical simulation of cellar structures and mach reflection of gaseous detonation waves [J]. Explosion and Shock Waves, 2001, 21(3): 161-163. (in Chinese)

[15] NING Jian-guo, CHEN Lun-wei. Fuzzy interface treatment in Eulerian method [J]. Science in China (Series E): Engineering & Materials Science, 2004, 47(5): 550-568. (in Chinese)

[16] OU Jian-ping, MA Ai-chun, ZHAN Shu-hua, ZHOU Jie-min, XIAO Ze-qiang. Dynamic simulation on effect of flame arrangement on thermal process of regenerative reheating furnace [J]. Journal of Central South University of Technology, 2007, 14(2): 243-247.

[17] WANG Gang, LIU Shao-jun, LI Li. FEM modeling for 3D dynamic analysis of deep-ocean mining pipeline and its experimental verification [J]. Journal of Central South University of Technology, 2007, 14(6): 808-813.

[18] ZHANG Bao-ping, ZHANG Qing-ming, HUANG Feng-lei. Detonation physics [M]. Beijing: Ordnance Industry Press, 2001. (in Chinese)

[19] PILLIOD J E, PUCKETT E G. Second-order accurate volume-of-fluid algorithms for tracking material interfaces [J]. Journal of Computational Physics, 2004, 199(2): 465-502.

[20] FAN Xi-sheng. The actuality and study orientation of the combustible gas explosion in pipeline [J]. Industrial Safety and Dust Control, 1998(6): 10-15. (in Chinese)

[21] XU Guo-yuan, GU De-sheng. Experimental investigation on generation mechanism of explosive stress wavels [J]. Transactions of Nonferrous Metals Society of China, 1999, 9(2): 433-436.

[22] XIE Fei-hong, LUO Guan-wei, LIAO Jun-sheng. Numerical analysis of explosive welding interface layer based on δ function [J]. The Chinese Journal of Nonferrous Metals, 2007, 17(12): 2029-2033. (in Chinese)

(Edited by YANG Hua)

Foundation item: Project(10572026) supported by the National Natural Science Foundation of China

Received date: 2008-01-05; Accepted date: 2008-03-24

Corresponding author: WANG Cheng, Associate professor, PhD; Tel: +86-10-68912762; E-mail: wangcheng@bit.edu.cn