DOI： 10.11817/j.issn.1672-7207.2019.12.012

基于传递熵和改进替代数据法的损伤识别

叶昌鹏¹,刘国华¹,何先龙²,谢中凯³,王振宇¹

（1. 浙江大学 建筑工程学院，浙江 杭州，310058；

2. 中国地震局工程力学研究所，黑龙江 哈尔滨，150080；

3. 浙江省水利河口研究院，浙江 杭州，310020）

摘要:为了提高传递熵方法对结构损伤识别的精度和可靠性，提出一个具有一定置信水平的损伤指标，由相对基准数据和置信水平确定置信区间范围，计算各时间延滞处由替代数据与原始数据算得的传递熵之差的绝对值，对落在该置信区间范围外的绝对值加权求和。采用传递熵和改进替代数据法对带裂缝梁的数值模型进行损伤识别研究，并对含法兰损伤的风电塔筒进行损伤识别。研究结果表明：悬臂梁上裂缝附近测点组的损伤指标与裂缝长度呈明显正相关关系，通过损伤指标能够识别裂缝长度变化，验证了算法和指标的有效性。法兰维修后的风电塔筒上测点组的损伤指标相对较小。依据该损伤指标，采用传递熵和改进替代数据法能够进行非线性损伤识别。

关键词:损伤识别；传递熵；改进替代数据法；损伤指标；风电塔筒法兰损伤；非线性损伤

中图分类号:TU317;TU511    文献标志码:A     文章编号:1672-7207（2019）12-3023-12

Damage identification based on transfer entropy and improved surrogate data method

YE　Changpeng¹, LIU　Guohua¹, HE　Xianlong², XIE　Zhongkai³, WANG　Zhenyu¹

(1. College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, China；

2. Institute of Engineering Mechanics, China Earthquake Administration, Harbin 150080, China；

3. Zhejiang Institute of Hydraulics & Estuary, Hangzhou 310020, China)

Abstract: In order to improve the accuracy and reliability of the structural damage identification by the transfer entropy method, a damage index combined with a certain level of confidence was proposed. The range of the confidence interval was determined from the relative baseline data and the confidence level, and the absolute values of the difference between the transfer entropy calculated from the surrogate data and the transfer entropy calculated from the original data were calculated at each time delay, and the absolute values that fall outside the bounds of the confidence interval were weighted and summed. The damage identification of the numerical model of cracked beams was studied by using the transfer entropy and the improved surrogate data method. The method was used to further identify the damage of the wind turbine tower with flange damage. The results show that the damage index values of the measuring point groups near the crack on the cantilever beam are positively correlated with the crack length. The length change of the crack is identified by using the damage index, and the effectiveness of the algorithm and damage index is verified. The damage index values of the measuring point groups on the wind turbine tower after repairing the flange are relatively small. According to the damage index, the transfer entropy and the improved surrogate data method can be applied to nonlinear damage identification.

Key words: damage identification; transfer entropy; improved surrogate data method; damage index; wind turbine tower flange damage; nonlinear damage

结构中的损伤通常被认为具有非线性特征，而健康状态下的结构性状为线性^[1]。结构损伤将导致结构的力学特性发生变化，从而使振动响应信号出现异常^[2]。在时域上，振动信号呈现无序，有时会产生拍振现象；在频域上，信号频率组分增多，并且特征频率会变得分离^[3]。在土木工程领域，传递熵理论已被应用于风电机组故障穿越识别和振动传递路径识别，同时也被应用于结构损伤识别^[4-6]。邵长利^[7]利用线性化传递熵对三层结构多种损伤类型进行识别，发现线性化传递熵对线性损伤工况下损伤识别效果很好，但无法准确判断非线性损伤情况。谢中凯等^[8]利用数值分析方法模拟高斯白噪声激励下的损伤简支梁，通过对梁上多点的加速度信号进行传递熵计算，对比分析线性化传递熵结果与核密度估计传递熵结果，验证使用线性化传递熵的合理性。线性化传递熵需要依赖结构的损伤为线弹性的假设，该假设与实际的力学特征存在较大不同，并且要求外部激励为高斯激励，因此，该方法在实际工程问题中的运用受到限制，而基于核密度估计的传递熵则适用于任意平稳激励的非线性损伤问题。OVERBEY等^[9]利用双时间因子传递熵计算得到双时间尺度上的熵值曲面，从而更加全面地描述信号间的传递关系，该方法比单一时间因子的传递熵方法更敏感，而且可以识别损伤的位置。但是在实际运用中，考虑到传递熵的计算过程需要进行多种概率密度的评估，如果对非线性损伤问题使用双时间因子传递熵，那么计算的规模将非常巨大，因此，双时间因子传递熵在实际运用中受到极大的限制。传递熵算法用于结构损伤识别时，替代数据方法^[10]被用于摆脱对结构初始状态响应数据的依赖。NICHOLS等^[11-12]分别利用传递熵和互信息算法，并结合替代数据方法对一个具有后屈曲特性的五自由度弹簧振子系统进行非线性程度评估，发现传递熵的敏感性要优于互信息方法的敏感性，能够更好地识别出结构的非线性特性；他们在利用改进替代数据法时，采用“随机洗牌”算法打乱相位，然后利用时间延滞传递熵，对原始数据和替代数据进行计算，诊断了厚复合夹层板中的冲击损伤。他们提出了2种损伤指标，摆脱了对基准数据的依赖，用由原始数据算得传递熵与由多组替代数据算得的传递熵的平均值在各个延滞时间处做差值，用差值是否落在置信区间范围之内来判断响应数据是否具有非线性特征。对由多组替代数据算得的传递熵在各延滞时间处做均值处理容易丢失细节信息，并且替代数据的产生存在偶然性，若替代数据的组数不足，则容易导致产生错误的置信区间。LIU等^[13-14]基于多组替代数据算得传递熵的离散性，提出了一个非线性指标，利用传递熵和替代数据方法识别出损伤圆柱壳振动信号中的非线性特征，同时也利用该指标有效地识别出层合板的几何非线性和荷载的变化。但所提出的指标并未与统计学中的置信区间相结合，没有充分体现替代数据方法具有偶然性的特征。因此，有必要建立一个新的损伤指标，来发挥传递熵方法在损伤识别领域的优势。前人利用传递熵进行损伤识别研究时，基本使用结构数值解、解析解或者室内试验所得数据，数据质量容易受控制，无法充分表现传递熵和替代数据方法的适用范围。本文作者借鉴其他学者构造传递熵损伤指标的思路^[11-12]，提出一个具有一定置信水平的损伤指标。利用基于核密度估计的传递熵算法和改进的替代数据方法，对带裂缝竖直悬臂梁的数值解和法兰维修前后的风电塔筒的实测振动数据进行计算分析，验证所提出损伤指标的有效性，为传递熵和改进的替代数据方法用于实际工程的非线性损伤识别提供一种途径。

1 损伤识别方法

SHANNON^[15]提出了信息熵，将熵的概念与信息论结合，用之度量系统整体性^[16]。系统越无序，不确定性越大，则信息熵较高，反之，信息熵则较低^[17]。

信息熵公式离散形式：

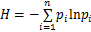(1)

信息熵公式连续形式：

(2)

式中：p_i为信息源中第i种信号出现的概率；ln p_i 为第i种信号的信息量；n为信号的长度；H为信息熵。SCHREIBER^[18]基于信息熵理论提出传递熵算法，用以定量描述不同时间序列之间的耦合关系以及信息传递关系。

1.1　基于核密度估计算法的传递熵

进程x与y为2个平稳的马尔可夫过程，并且在已知进程x的全部历史信息的条件下，进程y对进程x将来的某一时刻状态提供额外的描述信息，可以用传递熵来衡量。基于进程x与进程y之间的动态相互依赖性，传递熵公式为^[18]

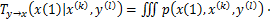
(3)

式中：k和l分别为进程x与y的阶数。为了减少评估高维度概率密度时所需的计算量，NICHOLS等^{[11-12,19-20]}建议假定进程x与y均为一阶马尔可夫过程^[11,19-20]，即k=l=1，从而简化了描述结构动态信息之间的传递关系的过程。在上述假定下，对式(3)中的进程y考虑添加一个时间延滞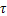，则可得到单一时间因子的时间延滞传递熵^[11]：

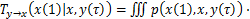
(4)

对于进程x(n)中的每个点，都可采用如下形式的核密度估计^[20]：

(5)

式中：N为数据序列的长度；为单位阶跃函数，其数学表达形式为

运算符号||·||表示求距离范数运算；h为Theiler窗口的尺寸，用于去除时间相关点的影响^[21]和消除使用核密度估计方法所产生的偏差^[22]，建议取值为10~100^[23]；ε为带宽，由结构确定所要忽略的尺寸^[22]，建议取值为时间序列标准差的2.5%~12.5%^[11]。一般在计算前先将时程序列进行归一化处理。

PRICHARD等^[24]提出将进程x(n)的信息熵近似记为

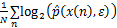(6)

考虑到条件概率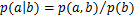，并将式(6)代入式(4)，则基于核密度估计的传递熵为

(7)

对于实际工程或者室内实验而言，时程数据的长度是有限的，但只要这类数据能满足平稳和各态遍历的条件，就可以对数据使用核密度估计方法^[11-12]。式(7)适用于线性数据和非线性数据，属于一种通用的算法。

1.2　改进的替代数据方法

对于很多的实际工程结构，很难获得或者根本没有最初状态的监测数据，这就使得那些基于结构初始状态的非线性损伤识别方法无法用于实际工程结构的非线性损伤分析，只能用于实验室内可人为控制的非线性损伤实验中。为解决上述问题，NICHOLS等^[11]利用传递熵结合替代数据方法对结构的非线性损伤问题进行研究。替代数据基于原始信号生成，保留原始数据的线性互相关关系，随机打乱任何高阶关系^[11]。利用基于核密度估计的传递熵算法对原始数据和替代数据分别进行计算，若熵值出现偏离，则表征信号中存在非线性耦合特性。

普通的替代数据方法只适用于完全满足高斯分布特性的随机数据序列，对于一般不具备高斯分布特性的随机数据序列需要引入改进的替代数据方法。改进的替代数据方法^[25]不仅保留了原始信号的线性相关特性，而且还保留原始信号的幅值分布特性，适用于任意具有平稳特性的时间序列。改进的替代数据方法采用“随机洗牌”算法^[25]或“幅值调整傅里叶变换”算法^[26]来打乱原始数据的相位。经研究发现，与“随机洗牌”算法相比，“幅值调整傅里叶变换”算法计算结果相对稳定，不会产生与原始数据的功率谱或者相关函数差异较大的替代数据，利于后续迭代步骤的进行^[21]。因此，本文采用“幅值调整傅里叶变换”算法。

1.3　传递熵损伤指标

首先，将相对基准状态定义为时程响应具有一定的非线性特征的结构状态，可以任意选取，一般建议取刚刚经过修复或者比较完好的状态，以此构造判据来判断非线性损伤程度是否增加。假设由各组替代数据计算得到的传递熵在各时间延滞处均符合高斯分布，当各时间延滞处由原始数据和替代数据计算得到的传递熵的差值落在置信区间范围之内时，判定与相对基准状态的结构相比，该状态下结构非线性损伤程度没有增加，反之，则表示该状态下结构非线性损伤程度增加。定义损伤指标如下：

(8)

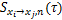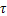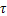式中：为分别由相对基准状态数据的N_s组替代数据算得的传递熵在不同时间延滞时的标准差，N_s越大，由替代数据产生的偶然性误差越小，本文后续2个算例中N_s都取100；为由第n组替代数据计算得到的时间延滞为时的传递熵；为由原始数据计算得到的时间延滞为时的传递熵。当显著性水平为α，即置信水平为1-α时，由于是双边检验问题，因此，临界值S=Z_α/2，损伤指标为

(9)

式中：n₀为替代数据的组数；为计算的时间延滞。对于各个状况而言，置信区间由，和临界值S决定，即，会随着相对基准数据的替代数据组数的增加而趋于稳定，因此，这种方法构造的置信区间的偶然性误差小，稳定性比文献[11-12]中方法的稳定性要好。对n₀组由替代数据算得的传递熵在各个延滞时间处落在置信区间外的值进行加权累加，不忽略由替代数据算得的传递熵的细节信息，从而能全面地衡量分别由原始数据和替代数据算得传递熵的偏差程度。

考虑到传递熵具有非对称性和双向性，为了能更加全面地衡量节点间的信息耦合关系，减小偶然性，对节点间2个方向的传递熵损伤指标进行平均化处理，从而得到节点间的传递熵最终损伤指标：

(10)

＞0，说明在置信水平为1-α条件下，与相对基准状态的结构相比，该状态结构的信号间传递的非线性特征增加，即结构非线性损伤程度增加。

2 带裂缝的悬臂梁数值分析

2.1　悬臂梁数值模型

建立如图1所示的钢材悬臂梁数值模型，梁的顶部受到一个高斯白噪声激励F(t)作用。假定梁只在主平面内振动，将问题简化为二维问题，以便缩短动力计算所需时间。利用Ansys软件的二维面面接触模型去模拟裂缝在振动过程中的开闭行为，裂缝接触面只考虑法向压力，而不考虑拉力和切向摩擦力。悬臂梁的跨中位置存在1条沿水平方向开展的裂缝。二维悬臂梁的竖向长度L=30.0 m，梁截面高度h₀=2 m，弹性模量E为210 GPa，泊松比ν为0.3，密度ρ为7 900 kg/m³。

图1　带裂缝竖直向悬臂梁数值模型

Fig. 1　Numerical model of vertical cantilever beam with crack

用裂缝长度来表示悬臂梁的损伤等级，裂缝的长度越长，则梁的损伤等级越高。裂缝长度分别取0.1h₀，0.2h₀，0.3h₀和0.4h₀，对应损伤等级分别为1，2，3和4。将无裂缝的完整梁作为相对基准状态，该情况下梁的振动保持线弹性，对应损伤等级为0。在受迫振动过程中，裂缝发生了开闭行为，该接触问题属于状态非线性的范畴，因此，由裂缝存在而导致的损伤属于非线性损伤。

在图1所示的10个测点处采集梁的水平向加速度响应时程，相邻测点距离为0.8 m，均匀分布在裂缝所在位置的两侧。模型的采样时间为10 s，采样频率为1 kHz，各种损伤工况下都选取后8 s的时程响应结果，计算数据长度为8 000。该算例中，核密度估计参数Theiler窗口尺寸h取为50^[23],带宽取为5%^[11]。

2.2　损伤识别结果

2.2.1　传递熵计算结果及分析　

在5种损伤等级下，在悬臂梁的顶部都受到相同的高斯白噪声激励F(t)，通过非线性动力有限元分析，分别获得10个测点的水平向加速度时程。对各损伤等级下的水平向加速度响应结果，分别使用改进的替代数据方法产生10组替代数据。经ADF(augmented dickey-fuller)平稳性检验表明，不同测点的上述各组数据在置信水平为99%的情况下均符合平稳性要求，即适用于核密度估计传递熵的计算。在各损伤等级状况下，分别对如图1所示的相邻2个点的水平向加速度时程的原始数据和替代数据进行传递熵计算。

图2所示为损伤等级为0，2和4时2种数据的传递熵结果。0级损伤时，分别由10组替代数据计算得到的各测点组的传递熵的离散性都较小，并且与由相应的原始数据算得的传递熵近似相等。这是因为0级损伤时，悬臂钢梁结构为线弹性，加速度振动响应时程不带有非线性特性，每次随机生成的替代数据包含的信息量基本与其相应的原始数据相同，从而使得由原始数据和替代数据分别计算得到的同一时间延滞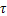的传递熵，相互之间的偏差很小。由替代数据计算得到的传递熵的曲线没有完全重合，即式(8)中不会出现为0的情况，因此，0级损伤可以作为相对基准状态，该损伤等级的作为构造同类结构的损伤指标相对基准值。

由图2可知，对于传递熵，随着损伤等级的增加，导致振动响应时程包含越来越多的非线性特性，替代数据与原始数据两者的非线性信息的差异增大，不同组替代数据的非线性信息的差异也增大，导致分别由10组替代数据算得的传递熵出现了越来越大的离散性，并且与由原始数据算得的传递熵的偏离也增大。但是随着损伤等级的增加，测点1与测点2之间的传递熵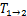不存在这样的趋势，分别由其原始数据和替代数据计算得到的传递熵之间的偏差程度变化不大。

图2　不同损伤等级不同数据计算下的传递熵

Fig. 2　Transfer entropy calculated by different data at different damage levels

2.2.2　损伤指标结果分析　

为了更直观地表示传递熵的计算结果，通过损伤指标来定量评估结构的损伤程度，并通过与NICHOLS等^[12]提出的损伤指标进行对比，以此验证本文提出的损伤指标的有效性。为了方便与本文提出的损伤指标作比较，用式(10)对其进行平均化处理。

图3所示为2种损伤指标的计算结果。由图3(a)可以发现，Nichols方法计算的损伤指标的变化趋势与损伤等级的变化不相应，没有准确表达图2中不同损伤等级下由2种数据算得的传递熵的差异。因此，使用该指标无法识别本算例的非线性损伤。由图3(b)可以发现，随着损伤等级的变大，损伤指标逐渐增大。裂缝处于测点5和测点6之间，悬臂梁在受到高斯白噪声作用会造成裂缝的开闭，从而导致裂缝附近的点的振动响应具有非线性特征。在本算例的裂缝长度范围内，非线性特征随着裂缝长度的变大而增大，从而导致由不同组替代数据计算得到的传递熵的离散性变大，并且与由原始数据计算得到的传递熵的偏差变大。在损伤等级变大的过程中，损伤指标和总体上也呈明显上升趋势。3组测点都位于裂缝附近位置，它们的传递熵损伤指标与裂缝长度存在明显的正相关关系。当测点组位置离裂缝有一定距离时，裂缝开闭行为对这些测点组时程响应的非线性程度影响减弱，因此，这些测点组的损伤指标没有随着损伤等级的增大而明显增大，即与裂缝长度不存在正相关关系。

图3　2种损伤指标结果对比

Fig. 3　Comparison of results of two kinds of damage indexes

图3(c)所示结果的变化规律与图3(b)的相类似，需要特别指出的是，在置信水平为97.5%情况下，位于裂缝附近位置的3组测点的损伤指标与裂缝长度存在正相关关系。置信水平越高，置信区间则越大，对于相同的损伤等级下的传递熵结果而言，会导致落在置信区间之外的点数量减少。由于式(9)考虑了置信水平，因此，置信水平的增加往往会使本文所提出的损伤指标变大。

在置信水平为95%时，Nichols方法计算的指标不能有效衡量各个裂缝长度下分别由2种数据算得的传递熵差异；而在2种置信水平情况下，本文所提出的损伤指标都能很好地与裂缝长度的增长情况相符合。随着裂缝长度增加，即损伤等级增大，附近测点的损伤指标增大。因此，依据所提出的损伤指标，传递熵结合改进替代数据方法能识别和大致定位悬臂梁结构的损伤。

3 风电塔筒损伤测试分析

3.1　测试数据

风电塔筒通过基础法兰固定在地基上，可以将之视为一个悬臂结构。

采集2台风电塔筒的振动速度时程，其中，Ⅰ号塔筒的法兰存在间隙和扭转错位的损伤情况，现场检查发现的损伤分布情况如表1所示；Ⅱ号塔筒运行时间久，运行状态良好视为不存在损伤。对有损伤的Ⅰ号塔筒在维修前后各测试1次，对Ⅱ号塔筒只测试1次，并将Ⅱ号塔筒的测试数据作为相对基准数据。

表1　3对法兰的损伤统计

Table 1　Damage statistics of three pairs of flange

由于法兰之间间隙和扭转错动的存在，风电塔筒在受外界荷载激励作用发生振动时，上下法兰之间的接触条件在振动过程中会随时间变化，属于状态非线性问题。

风机塔筒总高度为80 m。第1对法兰距离基础法兰的高度为11.215 m，外径为4.100 m。第2对法兰距离基础法兰的高度为28.865 m，外径为3.815 m。第3对法兰距离基础法兰的高度为51.495 m，外径为3.435 m。在风电塔筒内壁上布置14个速度拾振器，速度拾振器布置，见图4，采样频率为200 Hz，采样时长为1 h。

图4　速度拾振器布置示意图

Fig. 4　Layout diagram of velocity vibration sensor

维修前后的Ⅰ号塔筒的6号和7号测点的振动时程如图5所示。从图5可知：同一种运行工况下，6号和7号测点的振动速度非常接近。风机测试时主要受环境荷载作用，由于维修后的风速比维修前的小，因此维修后的结构响应比维修前的小。在进行传递熵计算前，都会对时程数据进行归一化处理，风荷载对传递熵计算结果影响很小。

图5　法兰维修前后6号和7号速度拾振器的振动时程

Fig. 5　Vibration time history of position of No. 6 and 7 velocity vibration sensor before and after repairing flange

3.2　FFT频谱分析

对维修前后采集到的振动速度数据进行FFT频谱分析，频率分辨率为0.001 Hz。图6所示为维修前后的6号和7号测点的振动速度数据计算得到的FFT频谱。

塔筒的振动以超低频为主，因此，频谱图主要显示第1阶固有频率附近的分布。维修前塔筒第1阶主频为0.321 Hz，经过维修后主频为0.320 Hz，1阶固有振动频率变化很小，难以依靠固有振动频率的变化来识别风机塔筒法兰连接的损伤。

3.3　传递熵计算结果分析

根据图4，采用原始数据和替代数据分别对维修前后分别处于塔筒连接法兰上、下位置处的振动速度时程测试数据进行传递熵计算。根据前人的研究，在相同的时间延滞内，低采样频率更容易发挥传递熵识别较低等级损伤的优势，因为与高采样频率的传递熵相比，由低采样频率计算得到的传递熵会在更多的时间延滞处出现局部最小值，而局部最小值产生的位置往往是损伤敏感区。对于较高的损伤水平，较低的采样频率会丢失过多的细节信息^[23]。从图6可以发现，风电塔筒的振动属于低频振动，振动能量主要集中在0.320 Hz附近，并且在维修前风电塔筒法兰的损伤水平较低，因此较低采样频率的风电塔筒振动测试数据更容易发挥传递熵的损伤识别优势。考虑到传递熵的计算规模，并结合谢中凯^[23]的研究，对风电塔筒的采样数据每隔12，15，20个点取1个点，即采样频率分别变为200/12，200/15，200/20 Hz，3种情况的数据量均为8 000个点。

图6　法兰维修前后6号和7号速度拾振器实测振动的FFT频谱图

Fig. 6　Vibration FFT spectrum of position of No. 6 and 7 velocity vibration sensor before and after repairing flange

经ADF平稳性检验表明，上述3种采样频率得到的数据的原始数据和替代数据在置信水平为99%的情况下均符合平稳性要求，即适用于核密度估计传递熵的计算，同时结合改进替代数据方法进行非线性程度识别分析。核密度估计参数按Theiler窗口的尺h为60^[23]，带宽ε为7%^[11]。

图7所示为采样频率f_s为200/12 Hz时，维修前后测得数据的传递熵计算结果，包括由原始数据和10组替代数据计算得到时间延滞传递熵，时间延滞τ为1/f_s s；表示测点j的振动速度时程对测点i的振动速度时程变化的影响程度。

由图7(a)和(b)可知：维修前后的传递熵都在时间延滞τ为26的整数倍时出现局部最小值。这与NICHOLS等^[11,19,27]的研究结果相一致。图7(c)~(e)中的传递熵没有在时间延滞为26的整数倍时出现局部最小值，但是2个相连局部最小值之间的时间延滞差均约为26。这可能是受法兰扭转错位和间隙的影响，风电塔筒局部振动特性产生了变化。

由图7可知，同一个测点维修前由原始数据和10组替代数据分别计算得到的传递熵在其局部最小值的偏离程度都比维修后的大。产生局部最小值的位置往往是识别损伤的敏感区域^[23]，图7(b)表明：由维修后的2种数据计算得到的传递熵在局部最小值近似相等，在其他时间延滞处偏离也较小，说明数据具有较小的非线性特征。2种数据的传递熵都在局部最大值附近存在一定的偏离，但是比较同一个测点组维修前后的传递熵结果可以发现，维修后的偏离程度要比维修前的小。

图7　维修前后由风电塔筒法兰上下测点计算得到的传递熵

Fig. 7　Transfer entropy calculated from upper and lower measuring points of wind turbine tower flange

3.4　损伤指标结果评价

针对无法直接从图7定量评估风机损伤程度的问题，使用由式(8)~(10)构造的损伤指标去评价损伤程度。假设一直保持良好运行状态的Ⅱ号塔筒的法兰不存在损伤，将其测试数据作为相对基准数据来判断Ⅰ号塔筒的法兰损伤情况。在置信水平为95%的条件下，风电塔筒法兰的损伤指标如表2所示。

从表2可知，在本算例的3种采样频率下，对比维修前后Ⅰ号塔筒上的6个测点组间的传递熵损伤指标，可以发现：维修前的损伤指标总体比维修后的大，说明基于传递熵结合改进替代数据方法能有效识别风电塔筒法兰的损伤。

表2　风电塔筒上测点组的损伤指标

Table 2　Damage index value of measuring point groups of wind turbine tower

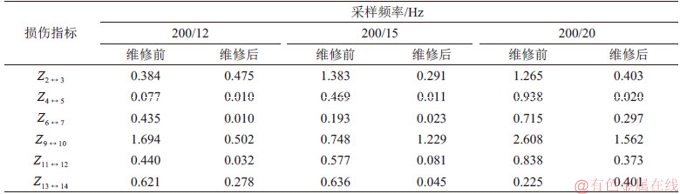
在3种采样频率下，损伤指标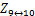，和分别存在1个异常点，即在某一采样频率时维修前的损伤指标略小于维修后的值，但两者数值相近。从表2也可以发现，当采用其他采样频率计算时，与未出现异常情况的测点组相比，维修后的损伤指标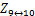，和均偏大。表明这些测点组附近法兰的损伤未得到充分的修复，导致该测点组的振动信号在维修之后仍具有一定的非线性特性。由于每一组替代数据都是随机产生，当维修前后法兰的损伤程度差别不大时，替代数据的偶然性可能会导致损伤指标上下波动，因此，表2中损伤指标在不同采样频率下的结果稍有不同。考虑到计算规模，本算例只产生了10组替代数据，如果计算足够多组的替代数据，可以避免这种偶然性。

4 结论

1) 提出了相对基准状态的概念和一个具有一定置信水平的损伤指标。假设由各组替代数据算得的传递熵在各时间延滞处均符合高斯分布，选取一个相对基准状态来确定一个置信区间去判定结构非线性程度是否增加，消除了替代数据算法偶然性对计算结果的影响，同时对多组替代数据的结果不作平均化处理，从而不会丢失由替代数据算得传递熵的细节信息。

2) 带裂缝悬臂梁算例的传递熵计算结果表明，增加裂缝长度会导致裂缝附近测点组的损伤指标明显增大，因此，可利用不同工况下测点组损伤指标的变化情况，采用传递熵结合改进替代数据方法识别悬臂梁结构的损伤。

3) 在风电塔筒损伤识别中，在难以依靠固有振动频率的变化来识别风机塔筒法兰连接损伤的情况下，对含法兰损伤的风电塔筒在3种采样频率情况下进行传递熵计算，计算结果表明传递熵有良好的损伤识别效果。

4) 以运行状况良好的风电塔筒的测试数据作为基准数据，采用所提出的损伤指标，对3种采样频率情况下法兰维修前后的传递熵进行计算，维修后各测点组的损伤指标小于维修前的结果，表明修复效果良好。

参考文献：

[1] WONG L A, CHEN J C. Damage identification of nonlinear structural systems[J]. AIAA Journal, 2000, 38: 1444-1452.

[2] MOUSAVI M, GANDOMI A H. An input-output damage detection method using static equivalent formulation of dynamic vibration[J]. Archives of Civil and Mechanical Engineering, 2018, 18(2): 508-514.

[3] PIOTRKOWSKI R, CASTRO E, GALLEGO A. Wavelet power, entropy and bispectrum applied to AE signals for damage identification and evaluation of corroded galvanized steel[J]. Mechanical Systems and Signal Processing, 2009, 23(2): 432-445.

[4] WU Zhenyu, SHANG Pengjian. Nonlinear transformation on the transfer entropy of financial time series[J]. Physica A: Statistical Mechanics and Its Applications, 2017, 482: 392-400.

[5] 陈子瑜, 李庆, 王伟胜. 传递熵算法在风电机组故障穿越特征分析中的应用[J].中国电机工程学报，2016, 36(14): 3751-3757.

CHEN Ziyu, LI Qing, WANG Weisheng. Characteristic analysis of wind turbine fault ride through procedure using transfer entropy[J]. Proceedings of the CSEE, 2016, 36(14): 3751-3757.

[6] 王海军, 王宁, 练继建. 基于传递熵的水电站厂房振动传递路径识别[J]. 水利学报, 2018, 49(6): 732-740.

WANG Haijun, WANG Ning, LIAN Jijian. Vibration transfer path identification of the hydropower house based on transfer entropy[J]. Journal of Hydraulic Engineering, 2018, 49(6): 732-740.

[7] 邵长利. 基于传递熵的工程结构损伤识别[D]. 广州: 暨南大学力学与建筑工程学院, 2014: 56-66.

SHAO Changli. Transfer entropy-based damage identification in engineering structures[D]. Guangzhou: Jinan University. School of Mechanical and Construction Engineering, 2014: 56-66.

[8] 谢中凯, 刘国华, 吴志根. 基于传递熵的梁结构损伤动力识别[J].浙江大学学报(工学版), 2012, 46(10): 1880-1886.

XIE Zhongkai, LIU Guohua, WU Zhigen. Dynamic damage identification for beam structures based on transfer entropy[J]. Journal of Zhejiang University(Engineering Science), 2012, 46(10): 1880-1886.

[9] OVERBEY L A, TODD M D. Dynamic system change detection using a modification of the transfer entropy[J]. Journal of Sound and Vibration, 2009, 322(1/2): 438-453.

[10] PRICHARD D, THEILER J. Generating surrogate data for time series with several simultaneously measured variables[J]. Physical Review Letters, 1994, 73(7): 951.

[11] NICHOLS J M, SEAVER M, TRICKEY S T. A method for detecting damage-induced nonlinearities in structures using information theory[J]. Journal of Sound and Vibration, 2006, 297(1/2): 1-16.

[12] NICHOLS J M, SEAVER M, TRICKEY S T, et al. Detecting impact damage in experimental composite structures: an information-theoretic approach[J]. Smart Materials and Structures, 2006, 15(2): 424-434.

[13] LIU Guohua, YU Ziyuan, LIANG Xu, et al. Vibration-based structural damage identification and evaluation for cylindrical shells using modified transfer entropy theory[J]. Journal of Pressure Vessel Technology, 2018, 140(6): 061204.

[14] LIU Guohua, YU Ziyuan, LIANG Xu, et al. Identification of nonlinearity using transfer entropy combined with surrogate data algorithm[J]. Journal of Engineering Mechanics, 2019, 145(2): 04018138.

[15] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3): 379-423.

[16] 龙文, 张文专, 焦建军. 基于组合进化算法的混沌时间序列重构相空间参数选取[J]. 中南大学学报(自然科学版), 2013, 44(8): 3246-3253.

LONG Wen, ZHANG Wenzhuan, JIAO Jianjun. Parameters determination based on combinative evolutionary algorithm for reconstructing phase-space in chaos time series[J]. Journal of Central South University(Science and Technology), 2013, 44(8): 3246-3253.

[17] 葛新民, 范宜仁, 唐利民, 等. 基于信息熵-模糊谱聚类的非均质碎屑岩储层孔隙结构分类[J]. 中南大学学报(自然科学版), 2015, 46(6): 2227-2235.

GE Xinmin, FAN Yiren, TANG Limin, et al. Pore structure typing of heterogeneous clastic reservoir using information entropy-fuzzy spectral clustering algorithm[J]. Journal of Central South University(Science and Technology), 2015, 46(6): 2227-2235.

[18] SCHREIBER T. Measuring information transfer[J]. Physical Review Letters, 2000, 85(2): 461.

[19] NICHOLS J M. Examining structural dynamics using information flow[J]. Probabilistic Engineering Mechanics, 2006, 21(4): 420-433.

[20] OVERBEY L A, TODD M D. Effects of noise on transfer entropy estimation for damage detection[J]. Mechanical Systems and Signal Processing, 2009, 23(7): 2178-2191.

[21] SUN Wanquan, YAN Dongming. Identification of the nonlinear vibration characteristics in hydropower house using transfer entropy[J]. Nonlinear Dynamics, 2014, 75(4): 673-691.

[22] KAISER A, SCHREIBER T. Information transfer in continuous processes[J]. Physica D: Nonlinear Phenomena, 2002, 166(1/2): 43-62.

[23] 谢中凯. 信息熵理论在混凝土结构损伤动力识别中的应用研究[D]. 杭州: 浙江大学建筑工程学院, 2013: 23-27.

XIE Zhongkai. A study on information entropy theory applied in vibration-based damage identification of concrete structures[D]. Hangzhou: Zhejiang University. College of Civil Engineering and Architecture, 2013: 23-27.

[24] PRICHARD D, THEILER J. Generalized redundancies for time series analysis[J]. Physica D: Nonlinear Phenomena, 1995, 84(3/4): 476-493.

[25] SCHREIBER T, SCHMITZ A. Improved surrogate data for nonlinearity tests[J]. Physical Review Letters, 1996, 77(4): 635.

[26] THEILER J, EUBANK S, LONGTIN A, et al. Testing for nonlinearity in time series: the method of surrogate data[J]. Physica D: Nonlinear Phenomena, 1992, 58(1/2/3/4): 77-94.

[27] 刘国华，谢中凯. 一种用于检测梁结构损伤的改进传递熵[J]. 振动工程学报, 2014, 27(1): 136-144.

LIU Guohua, XIE Zhongkai. A modified transfer entropy method for damage detection of beam structures[J]. Journal of Vibration Engineering, 2014, 27(1): 136-144.

（编辑 赵俊）

收稿日期： 2019 -01 -19; 修回日期： 2019 -04 -23

基金项目(Foundation item)：国家自然科学基金资助项目(51379185，51779224，51579221)；中国地震局工程力学研究所基本科研专项(2017B02)；浙江省水利科技计划项目(RC1601)(Projects(51379185, 51779224, 51579221) supported by the National Natural Science Foundation of China; Project(2017B02) supported by Basic Research of Institute of Engineering Mechanics, China Earthquake Administration; Project(RC1601) supported by Zhejiang Provincial Water Science and Technology)

通信作者：王振宇，博士，教授，从事水工结构、风机振动研究；E-mail：wzyu@zju.edu.cn