J. Cent. South Univ. Technol. (2008) 15(s1): 402-405

DOI: 10.1007/s11771-008-388-x

In-plane shear (ModeⅡ) crack sub-critical propagation of rock at high temperature

RAO Qiu-hua(饶秋华), XIE Hai-feng(谢海峰), XIE Qiang(谢 强)

(School of Civil Engineering and Architecture, Central South University, Changsha 410083, China)

Abstract: In-plane shear crack sub-critical propagation of rock at high temperature was studied by finite element method and shear-box (i.e. compression-shear) test with newly designed electrically conductive adhesive method. Numerical and experimental results show that the normalized shear (Mode Ⅱ) stress intensity factors, 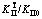 is decreased as the temperature increases because high temperature can improve stress distribution at crack tip and reduce the Mode Ⅱ stress intensity factor. Microscopic features of fractured surface are of little pits and secondary micro-cracks in the vicinity (1.5-4.0 mm) of the crack tip. The chevron-shape secondary cracks gradually merge in the length of about 4-5 mm and disappear along the direction of crack propagation. Stable shear crack propagation time is increased with the increasing temperature while the stable shear crack propagation rate is decreased with the increasing temperature, since high temperature can increase the shear (Mode II) fracture toughness and prevent the crack growth. It is necessary to ensure the ligament of specimen long enough to measure the maximum unstable crack propagation rate of rock.

Key words: sub-critical crack propagation; temperature; shear (Mode II) fracture; electrically conductive adhesive; rock

1 Introduction

In deep mining, geotechnical and radioactive waste disposal engineering, rock mass is not only subjected to in-plane shear (Mode Ⅱ) or compression-shear loading, but also subjected to high temperature and pressure. Temperature has a great effect on mechanical properties and fracture characteristics of rock. However, few literatures are reported for in-plane (Mode Ⅱ) fracture of rock at high temperature^[1-4].

Study of crack sub-critical propagation is of significance for the assessment of safety and prediction and control of disaster in structure of rock mass. At present, there are mainly three methods available for measuring the crack propagation, including optical method^[5-7], compliance method^[8] and electromagnetism method^[9]. These methods have main shortcomings of heavy testing machine and expensive cost, or strict requirement of optics and sound surroundings, or discontinuous monitoring of crack propagation process. It is necessary to propose a new method for continuous measurement of shear crack sub-critical propagation of rock.

In this study, shear-box (i.e. compression-shear) test and newly designed electrically conductive adhesive method were used to study the shear crack sub-critical propagation and fracture characteristics of sandstone specimen in order to find out a suitable method to determinate Mode Ⅱ fracture toughness and help crack arrest of rock at high temperature.

2 Numerical calculation

The compression-shear specimen is cubic with length L=50 mm, width W=50 mm, and height H=50 mm. The notch length a is 25 mm and the width t is 1 mm. The specimen is subjected to shear stress P_τ on areas A₁ and A₂ and compressive stress P_σ, as shown in Fig.1. The ratio of P_τ to P_σ depends on the inclined angle of beveled die, α. In this study α=70?.

The tested rock is red sandstone, from Yunnan Province. Table 1 lists the mechanical properties of sandstone at room temperature, based on the test standards of the International Society for Rock Mechanics (ISRM). Elastic modulus, E, is increased with the increase of temperature, as shown in Fig.2, and the Possion ratio is considered to be independent of temperature.

Finite element software MSC.Marc2005 was adopted to calculate stress field of rock specimen and Mode Ⅱ stress intensity factor(SIF), 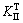 at high temperature (40, 60, 80 and 100 ℃) and K_II0 at room

Fig.1 Schematic diagram of compression-shear specimen

Table 1 Mechanical properties of sandstone at room tempera- ture

[A1] 

Fig.2 Elastic modulus varying with temperature

temperature (20 ℃) by displacement extrapolation method. The elements were hexahedron elements of eight nodes with homogenous properties. Since the distribution of the stress applied to the specimen surface in shear-box test was unknown, the specimen and loading setup were modeled as a whole (Fig.3). The applied load was assumed to be unit load 1 N.

Table 2 lists the numerical results of normalized Mode Ⅱstress intensity factors, 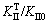 at different temperatures. It is found that  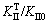is decreased as the temperature increases. That is probably because high temperature could improve stress distribution at crack tip and reduce the value of Mode Ⅱ stress intensity factor. It can be predicted that Mode Ⅱ fracture toughness K_IIC would be increased with the increase of temperature.

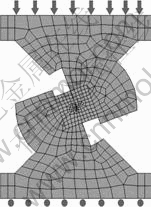
Fig.3 Finite element meshing configuration

3 Experimental

The tested specimen has the same dimension as that in numerical calculation (Table 2). The initial notch with sharp tip was prepared by a diamond saw blade with the thickness of 0.8 mm and an alloy drill bits. The notch length a was 25 mm and the notch width t was 1 mm. The vertical derivations and the parallelism of specimen surface were less than 0.25° and 0.05 mm, respectively.

Since rock is insulating material, the crack propagation process can be tracked by surface survey technology. It is possible to exactly measure the crack propagation rate of shear (Mode Ⅱ) fracture since its initiation and propagation occur along its original plane in compression-shear specimen^[10]. As shown in Fig.4(a), a layer of electrically conductive adhesive, 0.1 mm in thickness and 20 mm in width, was uniformly smeared symmetrically onto the original notch plane. It must be thin and uniform enough in order that it could be cracking at the same time as the specimen cracks. A closed loop was designed by DC stable voltage power, fixed resistance and variable resistance of specimen (caused by crack propagation) and connecting copper lines. A low and a high-frequency voltage sampling digital storage oscilloscopes were adopted to monitor shear crack stable (slow) and unstable (quick) propagation of rock specimen, respectively.

Before shear-box test (Fig.4(b)), sandstone specimens were heated at 40, 60, 80 and 100 ℃, for at least 2 h in order that the temperature was uniformly distributed in the whole of specimens.

All the compression-shear tests were performed by  the INSTRON1346 electro-hydraulic servo testing system, under a displacement control. The loading rate was 0.5 mm/min and the inclined angle of the beveled die, α, was 70?. The shear crack growth characters, including the crack initiation time, crack stable (sub-critical) propagation and unstable propagation rate were measured by newly-designed electrically conductive adhesive method, and microscopic characteristics of fractured surface were investigated by a scanning electron microscope (SEM).

Table 2 Dimensions of specimen and normalized SIF at different temperatures

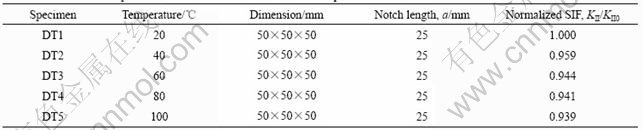
Fig.4 Shear-box test for shear crack propagation: (a) Specimen with electrically conductive adhesive; (b) Test set-up

4 Results and analysis

Fig.5 shows the microscopic features of fractured surfaces at different temperatures by SEM. It is seen that the damage of little pits and secondary micro-cracks exists in the vicinity (1.5-4.0 mm) of the crack tip. The radius of pits is 0.5 mm on average. The chevron-shape secondary cracks gradually merge in the length of about 4-5 mm and disappear along the direction of crack propagation. This means that the crack is initiated at the little pits and propagated 4-5 mm in length, i.e. forming a zone of sub-critical crack growth. The length of sub-critical crack propagation at high temperature (100 ℃) is a little larger than that at room temperature (20 ℃).

Fig.5 Microscopic features of fractured surfaces at different temperatures (C: Crack initiation orientation; P: Pits; S: Secondary crack; T: Crack tip): (a) Specimen DT1 at 20 ℃;  (b) Specimen DT5 at 100 ℃

Figs.6 and 7 show the stable and unstable crack propagation time and rate at different temperatures. It is found that the stable shear crack propagation time (about

Fig.6 Stable shear crack propagation time and rate varying with temperature

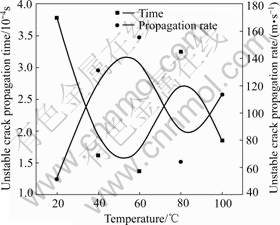
Fig.7 Unstable shear crack propagation time and rate varying with temperature

28-40 s) is increased with the increasing temperature, while the stable shear crack propagation rate ((1-2)×10^{-4 m/s) is decreased with the increasing temperature. This could be because the shear (Mode} Ⅱ) fracture toughness is increased as the temperature increases, which prevents the crack growth. However, the change of the unstable shear crack propagation time (2-4×10^-4 s) and rate (50-160 m/s) with the increasing temperature is discrete. This is probably because the ligament of specimen is not long enough to measure the maximum unstable crack propagation rate at different temperatures.

5 Conclusions

1) Normalized shear (Mode Ⅱ) stress intensity factor, 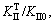is decreased as the temperature increases because high temperature can improve stress distribution at crack tip and reduce the Mode Ⅱ stress intensity factor.

2) Microscopic features of fractured surface are of   little pits and secondary micro-cracks in the vicinity (1.5-4.0 mm) of the crack tip. The chevron-shape secondary cracks gradually merge in the length of about 4-5 mm and disappear along the direction of crack propagation. The length of sub-critical crack propagation at high temperature (100 ℃) is a little larger than that at room temperature (20 ℃).

3) Stable shear crack propagation time is increased with the increasing temperature while the stable shear crack propagation rate is decreased with the increasing temperature. This is because high temperature can increase the shear (Mode II) fracture toughness and prevent the crack growth. It is necessary to ensure the ligament of specimen long enough to measure the maximum unstable crack propagation rate of rock.

[1] YU Yao-zhong, QIAO Chang-xin, ZHOU Qun-li. Fracture mechanics of rock and concrete [M]. Changsha: Central South University of Technology Press, 1991. (in Chinese)

[2] FAN Tian-you. Principal and application of dynamic fracture mechanics [M]. Beijing: Beijing Institute of Technology Press, 2006.

[3] TANG Chun-an. FU Yu-fang, ZHAO Wen. A new approach to numerical simulation of source development of earthquake [J]. Acta Seismological Sinica, 1997, 10(4): 425-434.

[4] JIAO Ming-ruo, ZHANG Guo-min. Study on genetic mechanism of seismic precursory complexity (II)—Genetic mechanism of complexity of seismic precursors [J]. Earthquake, 1998, 18(2): 112-118. (in Chinese)

[5] LIU Dong-mei, CAI Mei-feng, ZHOU Yu-bin, CHEN Zhi-yong. Dynamic monitoring on developing process of rock cracks [J].Chinese Journal of Rock Mechanics and Engineering, 2006, 25(3): 467-472. (in Chinese)

[6] XU Shi-lang, ZHAO Guo-fan. The stable propagation of crack in concrete and the determination of critical crack tip opening displacement [J]. 1989, 4: 33-44. (in Chinese )

[7] KAWAKATA H, CHO A, YANAGIDANI T, SHIMADA M. The observations of faulting in Westerly granite under triaxial compression by X-ray CT scan [J]. Int J Rock Mech & Min Sci, 1997, 34(3/4): 151-162.

[8] CICCOTTI M, GONZATO G, MULARGIA F. The double torsion loading configuration for fracture propagation: An improved methodology for the load-relaxation at constant displacement [J]. International Journal of Rock Mechanics and Mining Sciences,2000, 37(7): 1103-1113.

[9] XI Dao-ying, ZHONG Shi-jie, HUANG Xing-li. Study of growth speed of rock crack and inquiry of earthquake process [J]. Rock and Soil Mechanics, 1994, 14(3): 51-58. (in Chinese)

[10] RAO Qiu-hua. Pure shear fracture of brittle rock—A theoretical and laboratory study [D]. Sweden: Lule? University of Technology, 1999.

(Edited by LI Xiang-qun)

Foundation item: Project(50374073) supported by the National Natural Science Foundation of China; Project(1343-77239) supported by the Graduate Education Innovation Project of Central South University, China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: RAO Qiu-hua, Professor; Tel: +86-731-8836001; E-mail: raoqh@mail.csu.edu.cn