文章编号：1004-0609(2009)10-1880-06

Sm-Fe系薄膜悬臂板磁致伸缩行为的有限元模拟分析

周白杨，陈梓荣，骆汉彬，毛宏英，李  牣

(福州大学 材料科学与工程学院，福州 350108)

摘  要：以离子束溅射沉积(IBSD)法制备的Sm-Fe系超磁致伸缩薄膜悬臂板为研究对象，通过ANSYS有限元分析法，对超磁致伸缩薄膜/盖玻片衬底悬臂板自由端挠度值的大小进行模拟计算，并模拟Sm-Fe薄膜、Sm-Fe/Fe复合膜的内部磁化状态。结果表明：在薄膜与衬底厚度比较小的情况下，悬臂板端点挠度值随薄膜厚度的增加而线性增加，且与衬底厚度近似成二次抛物线关系，有限元分析结果与实测情况吻合较好；Sm-Fe单层膜内部磁力线分布较均匀；在Sm-Fe/Fe复合膜中，由于Fe膜的负磁场效应，使Sm-Fe膜内的磁力线分布出现不均匀的现象，且磁感应强度比Sm-Fe单层膜小。

关键词：Sm-Fe薄膜；离子束溅射；有限元；磁致伸缩

中图分类号：TM 27; TB 43       文献标识码： A

Finite element modeling of magnetostrictive behavior for

Sm-Fe system film cantilever

ZHOU Bai-yang, CHEN Zi-rong, LUO Han-bin, MAO Hong-ying, LI Ren

 (College of Materials Science and Engineering, Fuzhou University, Fuzhou 350108, China)

Abstract: Sm-Fe system giant magnetostrictive films were prepared by ion beam sputtering. The bending property of the giant magnetostrictive film/glass substrate cantilever was studied by finite element modeling. The internal magnetic states of the giant magnetostrictive films were simulated. The finite element analysis results show that the deflection is in direct proportion to the film thickness and quadratic parabola to the substrate thickness when the film thickness is much less than the substrate thickness. The analysis results are well comparable to the experiment ones. The internal magnetic field of Sm-Fe single film is uniform. Inside the Sm-Fe/Fe composite film, because of the negative magnetic effect of Fe film, the internal magnetic field of Sm-Fe film becomes nonuniform, and the magnetic induction is less than that of the Sm-Fe single film.

Key words: Sm-Fe film; ion beam sputtering; finite element; magnetostrictive

微型机电系统(MEMS)的研究和发展兴起于20世纪80年代末，是新的高技术产业增长点，被认为将导致21世纪一场新的产业革命。超磁致伸缩薄膜(Giant magnetostrictive thin films，简称GMF)是用于制作微机电系统执行元件的新型功能材料，它具有强的磁致伸缩效应、高机电耦合系数与响应速度、低磁滞与低涡流损耗以及非接触式驱动等优点，在MEMS中的智能结构材料方面具有重要的地位和很好的应用前景^[1-4]。

从目前的薄膜型超磁致伸缩微执行器的研究来看，主要采用的是悬臂板(悬臂梁)式和隔膜式，即将超磁致伸缩薄膜沉积在非磁性的玻璃、单晶硅或聚酰亚胺衬底上，利用外磁场变化使薄膜伸长或缩短从而带动衬底产生弯曲变形来实现输出或执行的功能。悬臂板自由端的挠度值和驱动力的大小除与磁致伸缩薄膜的磁致伸缩系数和弹性模量有关外，还与薄膜、衬底的厚度、薄膜的几何尺寸、衬底的弹性模量等性能有关。因此，分析悬臂板的弹性形变规律是磁致伸缩微执行器的设计基础。目前普遍采用的表征薄膜磁致伸缩性能的方法是由KLOKHOLM^[5]提出的，该方法假设薄膜内部磁化效应各向同性，忽略横向应变，采用能量最小原理推导出自由端挠度与磁致伸缩系数关系的解析表达式。考虑到外磁场的方向性导致磁致伸缩效应的各向异性，后来一些研究者，如DIRNE^[6]、du TREMOLET de LACHEISSERIE和PEUZIN ^[7]等对KLOKHOLM^[5]的结论进行了修正。在这些修正结果中，因悬臂板沿膜片宽度方向是否发生弯曲的假设不同，所得出的磁致伸缩系数的解析表达式有所不同。而公式推导过程中均假设薄膜的厚度远小于衬底厚度，且薄膜的长宽比较大，使用起来有较大的局限性。

近年来，随着稀土-铁超磁致伸缩材料的研究与发展，对稀土-铁超磁致伸缩材料的磁-机械耦合效应及其元器件设计的有限元数值分析方法研究得到了人们的重视^[8-10]。将有限元分析方法应用于超磁致伸缩薄膜弹性行为分析中，可以方便地对不同力学约束条件下、不同衬底材料的弹性行为及不同悬臂板结构在一定磁场下磁致伸缩薄膜的变形特性进行研究^[11-12]，特别是对难以通过实验进行研究的结果(如样品长宽比等因素的影响)进行分析。

超磁致伸缩薄膜磁化状态的改变是薄膜发生磁致伸缩现象的根本原因，研究薄膜的磁化特性对认识、了解超磁致伸缩薄膜的磁致伸缩机理至关重要。在传统的磁化曲线分析的基础上，引入有限元分析法，可以直观地描述薄膜内部的磁化情况，为研究薄膜的磁化特性做出补充和完善。

本文作者以离子束溅射法制备的Sm-Fe薄膜为研究对象，建立超磁致伸缩薄膜/盖玻片衬底(Sm-Fe/glass)悬臂板的有限元分析模型，对悬臂板样品的弹性形变规律进行研究；采用Ansys软件模拟了Sm-Fe单层、Sm-Fe/Fe复合膜的磁感应强度分布图。

1  实验

实验采用IBSD法制备Sm-Fe薄膜及Sm-Fe/Fe复合膜。靶材为真空熔铸的纯Fe、Sm-Fe合金靶，尺寸均为60 mm×60 mm×6 mm。衬底为经过化学抛光的盖玻片(25 mm×5 mm)。所有样品均在水冷基座上溅射沉积，溅射气体为高纯氩气(99.999%)。工艺参数如下：背底真空2.0×10^-5Pa，工作气压2×10^-2~3×10^-2Pa，放电电压50~100 V，束流电压800~1 500 V，加速电压300~350 V，束流电流15~20 mA。

2  Sm-Fe/glass悬臂板弹性变形的有限元分析

2.1  模型的建立

有限元计算软件包ANSYS可以对结构、热、流体及电磁场等多物理场进行分析，可以处理弹性体、非弹性体、流体、磁体及压电体的多物理场耦合问题，但它不能直接用于分析磁致伸缩效应，考虑到磁致伸缩材料在外磁场作用下的应力一应变本构关系为^[13]

而在温度场作用下的弹性体的应力―应变本构关系为

比较式(1)和(2)可知，磁致伸缩材料在单向外磁场作用下的应力―应变本构关系与弹性体在热场作用下的应力―应变本构关系类似。为此，利用ANSYS软件的热结构分析功能对磁致伸缩材料进行分析，即将磁致伸缩效应类比为薄膜各向异性的热膨胀效应，外磁场的作用类比为温度的作用。无约束条件下，薄膜在温度场θ的作用下沿X、Y和Z方向所产生的应变量为(α₁×θ，α₂×θ，α₃×θ)，其中α₁、α₂和α₃为3个方向的热膨胀系数。当薄膜在平行于X轴方向磁场H₁的作用下，磁性薄膜所产生的应变量为(q₁₁×H₁，q₁₂×H₁，q₁₃×H₁)；在平行于Y轴方向磁场H₂的作用下，磁性薄膜所产生的应变量为(q₂₁×H₂，q₂₂×H₂，q₂₃×H₂)。

采用ANSYS软件里的热膨胀模型模拟Sm-Fe薄膜的弹性行为，分析薄膜厚度、衬底厚度等对悬臂板自由端挠度值的影响。采用的单元类型为shell99二维壳层单元模型；根据样品的几何尺寸确定单元网格划分的尺寸，采用程序中所提供的智能网格划分方式(Smart size=8)进行网格划分。通过约束悬臂板一端的节点位移自由度，来模拟实际测量过程样品的夹持方式。对悬臂板施加温度场载荷(以外磁场强度H值代替)即可进行求解。计算中参数选取为：悬臂梁自由端长度L=16 mm，宽度W=5 mm，衬底弹性模量E_s=63.9 GPa，泊松比ν_s=0.24^[14]，Sm-Fe膜弹性模量E_f=80 GPa，泊松比ν_f=0.3，外磁场强度H=160 kA/m。

2.2  模型的验证

为了验证有限元ANSYS软件中的各向异性热膨胀模型是否适用悬臂板自由端扰度值的分析，实验采用离子束溅射法，分别在不同厚度的的盖玻片衬底上沉积Sm-Fe薄膜，采用电容—位移法测量样品的自由端偏转量；并分别进行200 ℃真空退火处理，再次测量其偏转量。样品A：衬底厚度为124 μm，薄膜厚度为0.592 μm ；样品B：衬底厚度为65 μm，薄膜厚度为0.587 μm。

根据测量得出的样品自由端偏转量D，薄膜的磁致伸缩系数λ^[15]由下式计算：

由式(3)可以求出相应的磁致伸缩系数，用磁致伸缩系数取代热膨胀模型中的热膨胀收缩系数，通过ANSYS软件计算出自由端挠度值(D)并与实测挠度值比较(见图1)。从图1中可以看出：有限元计算值与实际测量值相差小于5%(分析认为该误差主要是由计算薄膜磁致伸缩系数λ所采用的公式引起的，式(3)导出过程中所采用的部分假设条件与薄膜的实际情况仍有所偏差)。对比结果显示，有限元模拟值与实际测量情况吻合较好，因此，用有限元ANSYS软件分析悬臂板自由端扰度值是可行的。

图1  Sm-Fe薄膜的D―H曲线

Fig.1  D―H curves of Sm-Fe films: (a) As-deposited; (b) Annealed

2.3  薄膜厚度对挠度的影响

利用2.2节测得的磁致伸缩系数模拟Sm-Fe薄膜厚度对悬臂板端点挠度的影响。在衬底厚度d_s远大于薄膜厚度d_f(d_s?100d_f)的条件下，通过有限元软件分别在外磁场为160 kA/m下选取4种不同厚度的衬底，在固定的衬底厚度条件下，改变薄膜厚度模拟分析薄膜厚度对端点挠度值的影响，结果如图2所示。模拟结果表明端点挠度值与薄膜厚度近似成一次线性关系。

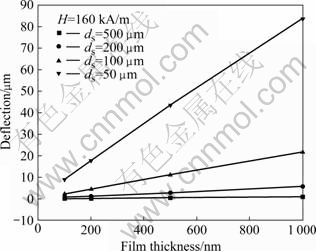
图2  当d_s?100d_f时薄膜厚度―挠度的曲线

Fig.2  Film thickness―deflection curves at d_s?100d_f

由于实际应用中衬底厚度总是远大于薄膜厚度，所以可以近似认为Sm-Fe薄膜厚度与悬臂板端点挠度值呈一次线性关系。

2.4  衬底厚度对挠度的影响

同样在衬底厚度远大于薄膜厚度的条件下，通过有限元软件在外磁场为160 kA/m下选取4种不同厚度的薄膜，在固定的薄膜厚度条件下，改变衬底厚度模拟分析衬底厚度对端点挠度的影响，其结果如图3所示。模拟结果表明：端点挠度与衬底厚度近似成二次抛物线关系，这与式(3)中薄膜及衬底厚度与悬臂梁自由端挠度值的关系相吻合。

图3  d_s?100d_f时的衬底厚度―挠度曲线

Fig.3  Substrate thickness―deflection curves at d_s?100d_f

3  Sm-Fe系薄膜内部磁场的有限元模拟分析

超磁致伸缩薄膜内部磁化磁场是薄膜对外部磁场作用的反映，也是薄膜磁致伸缩现象的直接磁动力。由于薄膜内部磁场无法实际测量和确定，同时超磁致伸缩薄膜本身是一种磁性材料并具有一定的磁导率，将其置于外磁场中势必会改变外磁场原有的大小和分布。如果将超磁致伸缩薄膜看成是外磁场中的一个磁性单元体，那么就可以通过有限元方法对薄膜内部的磁场大小及分布情况进行模拟和分析。

采用ANSYS 软件对Sm-Fe薄膜及Sm-Fe/Fe复合膜的内部磁场进行模拟，分析Fe膜的加入对磁场的影响。采用的单元类型为PLANE53单元模型。参数的选取如下：盖玻片衬底的磁导率为1，Fe膜的磁导率为18 000，Sm-Fe膜的磁导率为4 000(由磁化曲线得出)。模拟过程中假设磁化时薄膜的磁导率恒定不变。

图4所示为外磁场80 kA/m下Sm-Fe单层膜的磁感应强度B矢量分布及长轴方向等值图。

图4  Sm-Fe单层膜B矢量分布(a)及长轴方向等值图(b)

Fig.4  Sm-Fe film vector distribution of magnetic induction(a) and equivalence diagram of long axis(b)

从图4可以看出：Sm-Fe单层膜的中心部分被均匀磁化，磁力线分布比较均匀，且磁感应强度最大为529×10^-4~593×10^-4T，膜内两端磁化强度逐渐减小，这是由于受到空气介质被磁化所产生的负磁场效应，减弱了它两端的磁感应强度。薄膜两侧的磁感应强度最小为15×10^-4~79×10^-4T，这是薄膜对外界产生的负磁场效应所致。

图5所示为Sm-Fe_{540 nm}/Fe_{180 nm}复合膜(下标540 nm和180 nm分别为Sm-Fe膜和Fe膜厚度)的B矢量分布及长轴方向等值图。

图5  Sm-Fe_{540 nm}/Fe_{180 nm}复合膜的B矢量分布(a)及长轴方向等值图(b)

Fig.5  Sm-Fe_{540 nm}/Fe_{180 nm} composite film vector distribution of magnetic induction(a) and equivalence diagram of long axis(b)

从图5可以看出，Sm-Fe_540nm/Fe_180nm复合膜中的Sm-Fe膜的磁感应强度(213×10^-4~501×10^-4T)比Sm-Fe单层膜的小，由于Fe膜的磁导率(18 000)比Sm-Fe膜的磁导率(4000)大很多，因此，Fe膜在Sm-Fe与Fe的界面处会产生较大的负磁场效应，导致复合膜中Sm-Fe膜内磁矩通过交换耦合后出现磁感应强度不均匀现象，界面处的磁感应强度最小，而后沿着远离界面的方向逐渐增大。

超磁致伸缩多层膜是通过磁致伸缩材料与软磁材料交替沉积而成的，即由多层复合膜叠加组成；复合膜内部磁场的模拟分析可为研究超磁致伸缩多层膜的交换耦合作用提供重要依据。

4  结论

1) 在薄膜与衬底厚度比较小的情况下，悬臂梁自由端挠度值随薄膜厚度的增加而线性增加，且挠度值与衬底厚度近似成二次抛物线关系，有限元分析结果与实测情况吻合较好(误差小于5%)。

2) Sm-Fe单层膜内部磁力线分布较均匀；在Sm-Fe/Fe复合膜中，由于Fe膜的负磁场效应，使Sm-Fe膜内的磁力线分布出现不均匀的现象，且其磁感应强度比Sm-Fe单层膜的小。

REFERENCES

[1] HONDA T, ARAI K I, YAMAGUCHI M. Fabrication of magnetostrictive actuators using rare-earth (Tb, Sm)-Fe thin film[J]. J Appl Phys, 1994, 76(10): 6994-6998.

[2] QUANDT E, LUDWIG A. Magnetostrictive actuation in microsystems[J]. Sensors and Actuators, 2000, 81: 275-280.

[3] LIM S H, KIM H J, NA S M, SUH S J. Application-related properties of giant magnetostrictive thin films[J]. Journal of Magnetism and Magnetic Materials, 2002, 239: 546-550.

[4] 谢海涛, 斯永敏, 杨德明, 刘希从. 超磁致伸缩薄膜材料及其应用[J]. 中国有色金属学报, 2000, 10(增刊1 ): 266-270.
XIE Hai-tao, SI Yong-min, YANG De-ming, LIU Xi-cong. Giant magnetostrictive thin film and its application[J]. The Chinese Journal of Nonferrous Metal, 2000, 10(suppl.1): 266-270.

[5] KLOKHOLM E. The measurement of magnetostriction in ferromagnetic thin films[J]. IEEE Transactions on Magnetics, 1976, 12(6): 819-822.

[6] DIRNE F W A, DENISSEN C J M. Interface mixing in Fe/Co multilayers[J]. Journal of Magnetism and Magnetic Materials, 1989, 78(2): 122-128.

[7] du TREMOLET de LACHEISSERIE E, PEUZIN J C. Magnetostriction and internal stresses in thin films: The cantilever method revisited[J]. Journal of Magnetism and Magnetic Materials, 1994, 136(1/2): 189-196.

[8] 杨庆新, 阎荣格, 徐桂芝. 超磁致伸缩器件的数值计算模型[J]. 电子技术学报, 1999, 14(4): 17-20.
YANG Qing-xin, YAN Rong-ge, XU Gui-zhi. A numerical calculation model for giant magnetostrictive devices[J]. Transactions of China Electrotechnical Society, 1999, 14(4): 17-20.

[9] 孙 乐, 刘信恩, 郑晓静. 薄膜－基体型磁致伸缩微致动器的数值模拟[J]. 应用力学学报, 2004, 21(2): 41-45.
SUN Le, LIU Xin-en, ZHENG Xiao-jing. Numerical simulation of magnetostrictive film-substrate microactuators[J]. Chinese Journal of Applied Mechanics, 2004, 21(2): 41-45.

[10] 贾宇辉, 谭久彬. 超磁致伸缩驱动器及有限元分析方法的研究[J]. 光学精密工程, 2000, 8(2): 161-164.
JIA Yu-hui, TAN Jiu-bin. Giant magnetostrictive actuator and finite element model[J]. Optics and Precision Engineering, 2000, 8(2): 161-164.

[11] WESTON R S, CEDELL T. Finite elements solution to magnetostriction I: Harmonic modeling[J]. Finite Elements in Analysis and Design. 1998, 30: 187-196.

[12] 彭 彬, 张万里, 张文旭, 蒋洪川, 杨仕清. 磁致伸缩薄膜力学行为的有限元仿真研究[J]. 固体力学学报, 2006, 27(3): 288-292.
PENG Bin, ZHANG Wan-Li, ZHANG Wen-xu, JIANG Hong-chuan, YANG Shi-qing. Finite element simulations of the magnetostrictive film[J]. Acta Mechanica Solida Sinica, 2006, 27(3): 288-292.

[13] 万 红. TbDyFe薄膜的磁致伸缩性能及其与弹性、压电衬底复合效应研究[D]. 长沙: 国防科学技术大学, 2005.
WAN Hong. Studies on TbDyFe magnetostrictive film and its coupling effects with elastic or piezoelectric substrates[D]. Changsha: National University of Defense Technology, 2005.

[14] 毛宏英, 周白杨, 雷德辉, 汤乐明, 邓光华. Fe膜及磁场沉积对TbDy-Fe膜磁伸性能的影响[J]. 微细加工技术, 2008(3): 30-34.
MAO Hong-ying, ZHOU Bai-yang, LEI De-hui, TANG Le-ming, DENG Guang-hua. The effects of Fe film and field-sputtering on TbDy-Fe films magnetostriction[J]. Microfabrication Technology, 2008(3): 30-34.

[15] 姜 华, 周白杨, 陈鸿彬, 邓光华. 电容位移测量仪的校准与薄膜的磁致伸缩测量[J]. 理化检验: 物理分册, 2006, 42(5): 235-238.
JIANG Hua, ZHOU Bai-yang, CHEN Hong-bin, DENG Guang-hua. The calibration of capacitance-displacement micrometer and the measurement of the magnetostriction coefficient of thin films[J]. Physical Testing and Chemical Analysis Part A: Physical Testing, 2006, 42(5): 235-238.

(编辑 何学锋)