Phenomenon of transformed adiabatic shear band surrounded by

deformed adiabatic shear band of ductile metal

WANG Xue-bin(王学滨)

Department of Mechanics and Engineering Sciences, Liaoning Technical University, Fuxin 123000, China

Received 20 November 2007; accepted 31 March 2008

Abstract: The coexistent phenomenon of deformed and transformed adiabatic shear bands(ASBs) of ductile metal was analyzed using the JOHNSON-COOK model and gradient-dependent plasticity(GDP). The effects of melting point, density, heat capacity and work to heat conversion factor were investigated. Higher work to heat conversion factor, lower density, lower heat capacity and higher melting point lead to wider transformed ASB and higher local plastic shear deformation between deformed and transformed ASBs. Higher work to heat conversion factor, lower density, lower heat capacity and lower melting point cause higher local plastic shear deformation in the deformed ASB. Three reasons for the scatter in experimental data on the ASB width were pointed out and the advantages of the work were discussed. If the transformed ASB width is used to back-calculate the internal length parameter in the GDP, undoubtedly, the parameter will be extremely underestimated.

Key words: adiabatic shear band; ductile metal; deformation; transformation; JOHNSON-COOK model; gradient-dependent plasticity

1 Introduction

Adiabatic shear band(ASB) is formed by a process of thermo-mechanical instability. ASBs can be observed in various ferrous and nonferrous metals (such as titanium, aluminum and steels), alloys (such as titanium alloys, aluminum alloys and metallic glass), single crystals, polycrystals and polymers[1-7]. ASBs can be classified into deformed and transformed ASBs according to their appearance observed by optical microscopy[2-3]. The coexistent phenomenon of deformed and transformed ASBs has been observed by some researchers[8-11]. Usually, the central region of an ASB possesses the characteristics of the transformed ASB, while the transitional region between the matrix and the central region belongs to the deformed ASB (Fig.1). In Fig.1, the boundaries of the transformed ASB are marked.

Considering the effects of strain-hardening, strain-rate sensitivity, thermal-softening and microstructures, the JOHNSON-COOK(J-C) model and gradient-dependent plasticity(GDP) where an internal length parameter was included in the yield function to describe the interactions and interplay among microstructures were used to calculate the local temperature rise in the deformed ASB of Ti-6Al-4V[12]. Using the J-C model and GDP, the effects of constitutive parameters (such as static shear strength, strain-hardening modulus, strain-hardening exponent, strain rate sensitive coefficient and thermal-softening exponent) on the shear stress—average plastic shear strain curve, critical plastic shear strain, distributions of the local plastic shear strain and deformation in the ASB were investigated[13]. The effects of temperature and strain rate on the transformation onset, evolution of the transformed ASB thickness, temperature distribution in the ASB and local strain and deformation at interfaces between deformed and transformed ASB were studied[14]. The J-C model was respectively involved in the second-order GDP and fourth-order GDP to investigate the distributions of the local plastic shear strain and deformation in the ASB of three typical steels[15]. Aiming at the local total shear deformation distribution in the ASB of Ti-6Al-4V, the theoretical result based on the J-C model and GDP and that based on J-C model and measured flow shear stress—shear strain curve were compared with the experimental result[16].

Fig.1 Coexistent phenomenon of deformed and transformed ASBs in ultrafine-grained Fe[11]

The ZERILLI-ARMSTRONG model and GDP were adopted to investigate the effects of initial temperature on the distributions of the local plastic shear strain and deformation in the deformed ASB of aluminum-lithium alloy[17].

In this work, the coexistent phenomenon of deformed and transformed ASBs was investigated using the J-C model and GDP. The reasons for the scatter in experimental data on the ASB width and the advantages of the work were discussed.

The J-C model[12-15] was adopted to describe the shear stress—average plastic shear strain curve (τ— curve) of the ASB. When the shear stress τ reaches its maximum value, a deformed ASB with a finite thickness w appears (Fig.2).

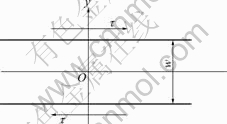
Fig.2 Deformed ASB subjected to shear stress

Using the GDP, WANG[12-15] derived the distribution γ_p(y) of the local plastic shear strain in the deformed ASB:

where  l is the internal length parameter reflecting the heterogeneity of ductile metal and l=w/(2π); y is the coordinate whose original point is set at the center O of the ASB (Fig.2); γ_c is the critical plastic shear strain that is the average plastic shear strain corresponding to the peak shear stress; and  is the average plastic shear strain of the ASB.

The total temperature distribution T(y) in the deformed ASB is the sum of the initial temperature T₀, the temperature rise T₁ at pre-peak and the temperature rise T_m(y) at post-peak due to the microstructural effect[12]:

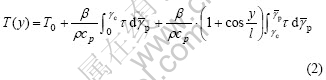
where  β is the work to heat conversion factor, c_p is the heat capacity and ρ is the density.

When the peak temperature T(0) in the deformed ASB is higher than the temperature T_p of transformation, transformation occurs in the form of dynamic recrystallization or phase transformation. A transformed ASB certainly appears in the center of the deformed  ASB, where there is much higher temperature. The thickness w_p of the transformed ASB cannot exceed w (Fig.3). On the two edges (y=±w_p/2) of the transformed ASB, the temperature is T_p. Thus, according to Eqn.(2), we have[14]

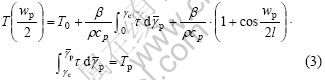
Using Eqn.(3), the expression for w_p is presented:

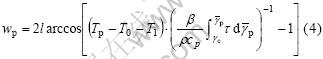
According to Eqn.(4), we can obtain the condition of transformation if w_p=0:

When |y|＞w_p/2, Eqn.(1) can be used to describe the distribution of the local plastic shear strain in the deformed ASB. When |y|＜w_p/2, Eqn.(1) cannot be adopted since experimental observations show no shear deformational traces in transformed ASB[1-7]. In the transformed ASB, i.e., |y|＜w_p/2, the local plastic shear strain always equates zero:

Integrating Eqn.(1) with respect to the coordinate y leads to the local plastic shear deformation s_p(y) in the deformed ASB[12-15]:

When |y|＞w_p/2, Eqn.(7) is applicable for the description of the local plastic shear deformation in the deformed ASB. However, when |y|＜w_p/2, the local plastic shear strain in the deformed ASB is always zero according to Eqn.(6). Thus, the local plastic shear deformation in the transformed ASB will be zero:

On the two edges (y=±w_p/2) of the transformed ASB, using Eqn.(1), the local plastic shear strain is

On the two edges of the transformed ASB, using Eqn.(7), the local plastic shear deformation is[14]

It is found from Eqn.(4) that if T_p＞T₀+T₁, the size w_p of the transformed ASB cannot exceed the width w of the deformed ASB. When w_p→w, we can obtain

When w_p→w, the deformed ASB will be completely converted into the transformed ASB. When w_p＜w, the coexistent phenomenon appears.

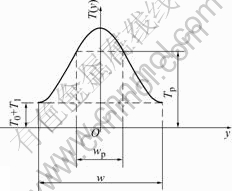
Fig.3 Transformed ASB in deformed ASB

3 Effects of parameters

3.1 Effects of work to heat conversion factor

Figs.4(a) and (b) show the influence of work to heat conversion factor β on the evolution of the thickness of the transformed ASB (τ—w_p curve) and the distribution of the local plastic shear deformation in the ASB (|y|—s_p(|y|) curve), respectively, with the static shear strength A=340 MPa, strain-hardening modulus B=200 MPa, strain rate sensitive coefficient C=0.03, thermal- softening exponent m=1.0, strain-hardening exponent n=0.3, melting temperature T_m=1 900 K, reference shear strain rate =10^-5 s^-1, imposed shear strain rate = 100 s^-1, c_p=500 J/(kg?K), T₀=300 K, ρ=4 500 kg/m³, T_p= 1 500 K and w=0.5 mm. The parameters A, B, C, m, n, , , , T₀, T_m, β, c_p and ρ are needed in the J-C model. The horizontal straight line in Fig.4(b) denotes the upper boundary of the transformed ASB.

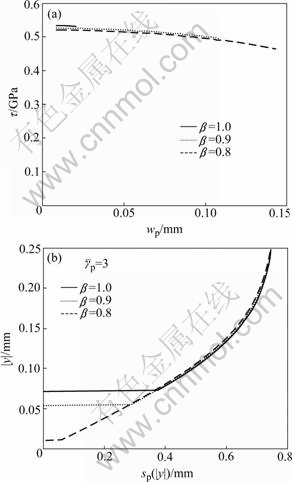
Fig.4 Effects of work to heat conversion factor β on thickness of transformed ASB (a) and local plastic shear deformation in ASB (b)

Fig.4(a) demonstrates that the thickness of the transformed ASB increases with the decrease of flow shear stress. Moreover, the τ—w_p curve is convex upwards and the increasing tendency of the thickness of the transformed ASB becomes slow. The flow shear stress is higher at higher work to heat conversion factor.

Fig.4(b) reveals that in the deformed region of the ASB, the distribution of the local plastic shear deformation is nonlinear. The thickness of the transformed ASB increases with work to heat conversion factor. In addition, the local plastic shear deformation at the boundary of the transformed ASB increases with the increase of work to heat conversion factor.

3.2 Effects of density

Figs.5(a) and (b) show the influence of density ρ on the curves τ—w_p and |y|—s_p(|y|), respectively, with w=0.5 mm, A=340 MPa, B=200 MPa, C=0.03, m=1.0, n=0.3, T_m=1 900 K, T_p=1 500 K, T₀=300 K, =10^-5 s^-1, c_p=500 J/(kg?K), =100 s^-1 and β=0.8. The upper boundary of the transformed ASB is marked in Fig.5(b).

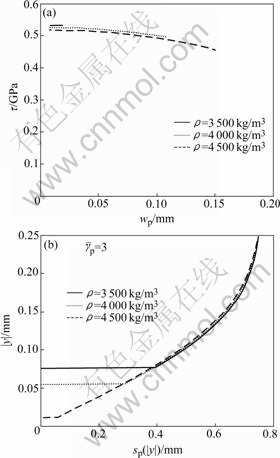
Fig.5 Effects of density ρ on thickness of transformed ASB (a) and local plastic shear deformation in ASB (b)

As density decreases, the shear stress decreases when transformation just occurs (Fig.5(a)); the size of the transformed ASB increases (Fig.5(b)) and the local plastic shear deformation in the boundary of the transformed ASB increases (Fig.5(b)).

3.3 Effects of heat capacity

Figs.6(a) and (b) show the influence of heat capacity c_p on the curves τ—w_p and |y|—s_p(|y|), respectively, with w=0.5 mm, A=340 MPa, B=200 MPa, C=0.03, m=1.0, n=0.3, T_m=1 900 K, T_p=1 500 K, T₀=300 K, ρ=4 500 kg/m³, =10^-5 s^-1, =100 s^-1 and β=0.8. The upper boundary of the transformed ASB is shown in Fig.6(b).

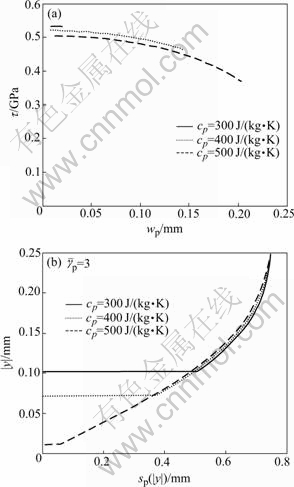
Fig.6 Effects of heat capacity c_p on thickness of transformed ASB (a) and local plastic shear deformation in ASB (b)

Figs.4-6 indicate that the effects of heat capacity on the curves τ—w_p and |y|—s_p(|y|) are similar to those of density and opposite to those of work to heat conversion factor.

3.4 Effects of melting temperature

Figs.7(a) and (b) show the influence of melting point T_m on the curves τ—w_p and |y|—s_p(|y|), respectively, with w=0.5 mm, A=340 MPa, B=200 MPa, C=0.03, m=1.0, n=0.3, T_p=1 500 K, T₀=300 K, ρ= 4 500 kg/m³, =10^-5 s^-1, =100 s^-1 , c_p=500 J/(kg?K) and β=0.8. The upper boundary of the transformed ASB is depicted in Fig.7(b).

When transformation occurs, lower melting temperature results in lower shear stress (Fig.7(a)), thinner transformed ASB (Fig.7(b)) and lower local plastic shear deformation on the boundary of the transformed ASB (Fig.7(b)).

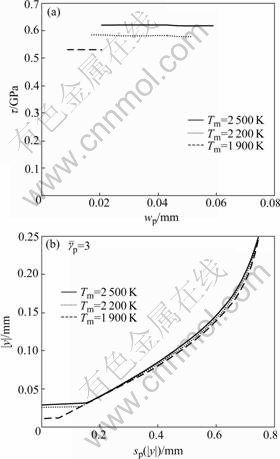
Fig.7 Effects of melting point T_m on thickness of transformed ASB (a) and local plastic shear deformation in ASB (b)

4 Discussion

4.1 Scatter in experimental data on ASB width

Herein, we will introduce the phenomenon of the scatter in experimental data on the ASB width of steels. MARCHAND and DUFFY[18] found that the lower bound of the ASB width for HY-100 steel was about 20 μm. However, the upper bound of the ASB width could approach 600 μm for HY 100 steel and 800 μm for 1018 cold-rolled steel.

To predict the ASB width numerically, investigations were carried out by some investigators. To model experimental results, BATRA and KIM[19] defined the ASB width as the width (w_5%) of the region surrounding the band center over which the plastic strain differed from its peak value by less than 5%[19-20]. The effect of higher order strain gradients on the ASB was investigated by ZHU and ZBIB[21] considering the simple shearing of a heat conducting thermoviscoplastic material with a gradient-dependent flow stress. ZHU and ZBIB[21] followed the definition about the ASB width proposed by BATRA and KIM[19] and the predicted lower bound of ASB width was slightly larger than the measured values of 0.19 mm by COSTIN et al and 0.2 mm by SEAMAN[21]. If the definition proposed by BATRA and KIM[19] was not taken into account, the predicted ASB width by ZHU and ZBIB[21] was in the order of millimeter, which was larger than most of the test data ranging from 20 μm to 0.6mm.

DODD and BAI[22] explained the reason for this. They believed that the observed widths were usually those of the transformed ASB, which was the central part of the deformed ASB only.

To the author’s knowledge, the viewpoint proposed by DODD and BAI[22] is accurate. The observed widths are usually those of the transformed ASB in which phase transformation or dynamic recrystallization occurs. LIAO and DUFFY[6] found that the ASB width ranged from 12-55 μm for Ti-6Al-4V in dynamic torsional experiments. Using the equation derived by DODD and BAI[22], the calculated value of the ASB width was 23 μm.

It should be noted that the measured value (12-55 μm) is the thickness of the central part of the deformed ASB rather than the total thickness of the ASB. The thickness of the deformed ASB is greatly larger than the measured value. WANG[16] newly calculated the thickness of the deformed ASB using the photograph given by LIAO and DUFFY[6] and found that it was in the order of millimeter. WANG[16] compared the experimental results of the local total shear deformation in the ASB[6] with the two kinds of theoretical results (the GDP was introduced into the J-C model and the experimentally measured shear stress—shear strain curve, respectively)[16]. In this study, the deformed ASB thickness of 2 mm was adopted. It was found that the agreement between the experimental and theoretical results was good. In addition, there was no clear evidence to suggest that the material within the ASB underwent a phase transformation, but a deformation- induced transformation was possible. Moreover, the boundaries between the ASB and the surrounding material were sharp and the curved flow lines could be observed in the surrounding material. Therefore, the so-called ASB[6] is possibly the central part of the ASB where a transformation is very possible. At least, dynamic recovery/recrystallization processes might take place. The so-called surrounding material[6] is possibly the deformed ASB. The total thickness of the ASB cannot be in the range of 12-55 μm.

The proposed equation by DODD and BAI[22] was widely adopted to calculate the ASB width. The predicted value using this equation is greatly less than the deformed ASB width, while approaches the width of the central part of the deformed ASB. Therefore, some researches only reported the experimental data about the width of the central part of the deformed ASB. The width of the central part of the deformed ASB is seen as the total width of the ASB. This viewpoint is not completely accurate since the wide region (about hundreds of microns, even approaching the order of millimeter) between the matrix and the transformed ASB is neglected in assessing the ASB width.

Herein, three reasons are attributed to the scatter experimental data about the ASB width:

1) The experimental materials, loading methods and experimental conditions are different.

2) The definitions of the ASB width are different.

3) Some researchers only report the width of the central part of the ASB to reach an agreement with the theoretical result by DODD and BAI[22].

4.2 Author’s work

In the equation about the ASB width derived by DODD and BAI[22], the thermal conductivity was taken into account. Moreover, a key assumption that after sufficiently long time the temperature profile will stabilize since the steady state balances the plastic work rate and the heat conduction was adopted by DODD and BAI[22]. The equation cannot be applied in adiabatic condition. Under this condition, thermal conductivity can be completely neglected. Thus, the ASB width cannot be predicted. In addition, the derived expression cannot be applied to predict the ASB width at earlier stage of shear localization. At this stage, the ASB is usually the deformed ASB.

Under adiabatic condition, the transformed ASB width can be assessed using Eqn.(4). It is found that the transformed ASB width is related to the internal length parameter, temperature of transformation, initial temperature, temperature rise at pre-peak and temperature rise due to the microstructural effect (at post-peak).

In the author’s work, the deformed ASB width is only associated with the internal length parameter in the GDP, reflecting the heterogeneity of ductile metal. In other words, the deformed ASB width is closely related to the effect of the second-order plastic shear strain gradient, i.e., the interactions and interplay among microstructures in heterogeneous ductile metal. However, the transformed ASB width is mainly controlled by the temperature distribution in the ASB (or the temperature rise at post-peak), as mentioned above. The upper bound of the transformed ASB width is the deformed ASB width. In theoretical analysis by the author, no assumption similar to the assumption (reaching a stable state) assumed by DODD and BAI[22] is used.

In the author’s work, once the internal length parameter is back-calculated from the deformed ASB width, the strain, deformation and temperature distributions in the ASB, thickness of the transformed ASB, critical strain corresponding to transformation and local strain and deformation at interfaces between transformed and deformed ASBs can be predicted numerically.

If the transformed ASB width is used to back-calculate the internal length parameter in the GDP, undoubtedly, the parameter will be extremely underestimated. Thus, much error can be involved in numerical and analytical solutions.

Results by the author cannot be applicable for extremely brittle metal materials since the localized deformation (or shear localization phenomenon) usually cannot be observed in these materials.

1) Higher heat conversion factor, lower density, lower heat capacity and higher melting temperature lead to wider transformed ASB and higher local plastic shear deformation between deformed and transformed ASBs. Higher heat conversion factor, lower density, lower heat capacity and lower melting point cause lower flow shear stress corresponding to transformation.

2) Three reasons are responsible for the scatter in experimental data on the ASB width: the difference in experimental materials, loading methods and experimental conditions, the difference in definitions of the ASB width and the inaccurate viewpoint that the width of the central part of the ASB is seen as the total width of the ASB. It is found that the total width of the ASB should be adopted to back-calculate the internal length parameter in the GDP, rather than the width of the transformed ASB.

[1] LIU Chu-ming, LIU Zi-juan, ZHU Xiu-rong, ZHOU Hai-tao. Research and development process of dynamic recrystallization in pure magnesium and its alloys [J]. The Chinese Journal of Nonferrous Metals, 2006, 16(1): 1-12. (in Chinese)

[2] XU Y B, WANG Z G, HUANG X L, XING D, BAI Y L. Microstructure of shear localization in low-carbon ferrite pearlite steel [J]. Mat Sci Eng A, 1989, A114(15): 81-87.

[3] GREBE H A, PAK H R, MEYERS M A. Adiabatic shear localization in titanium and Ti-6Al-4V alloy [J]. Metall Trans A, 1985, A16(5): 761-775.

[4] XUE Q, MEYERS M A, NESTERENKO V F. Self-organization of shear bands in titanium and Ti-6Al-4V alloy [J]. Acta Mat, 2002, 50(3): 575-596.

[5] LEE S, CHO K M, LEE C S, CHOO W Y. Microstructural study of adiabatic shear-band formed by ballistic impact in an HY-100 steel [J]. Metall Trans A, 1993, A24(10): 2217-2224.

[6] LIAO S C, DUFFY J. Adiabatic shear bands in a Ti-6Al-4V titanium alloy [J]. J Mech Phys Solids, 1998, 46(11): 2201-2231.

[7] YANG Yang, XIONG Jun, YANG Xu-yue. Microstructure evolution mechanism in adiabatic shear band in TA2 [J]. Trans Nonferrous Met Soc China, 2004, 14(4): 670-674.

[8] NAKKALIL R. Formation of adiabatic shear bands in eutectoid steels in high-strain rate compression [J]. Acta Metall Mat, 1991, 39(11): 2553-2563.

[9] XU Y B, LIU L, YU J Q, SHEN L T, BAI Y L. Thermoplastic shear localisation in titanium alloys during dynamic deformation [J]. Mat Sci Tech, 2000, 16(6): 609-611.

[10] MEBAR Y, SHECHTMAN D. On the adiabatic shear of Ti-6Al-4V ballistic targets [J]. Mat Sci Eng, 1983, 58(2): 181-188.

[11] WEI Q, KECSKES L, JIAO T, HARTWIG K T, RAMESH K T, MA E. Adiabatic shear banding in ultrafine-grained Fe processed by severe plastic deformation [J]. Acta Mat, 2004, 52(7): 1859-1869.

[12] WANG Xue-bin. Temperature distribution in adiabatic shear band for ductile metal based on Johnson-Cook and gradient plasticity models [J]. Trans Nonferrous Met Soc China, 2006, 16(2): 333-338.

[13] WANG Xue-bin. Effects of constitutive parameters on adiabatic shear localization for ductile metal based on Johnson-Cook and gradient plasticity models [J]. Trans Nonferrous Met Soc China, 2006, 16(6): 1362-1369.

[14] WANG X B. Effects of temperature and strain rate on the evolution of thickness of transformed adiabatic shear band [J]. Solid State Phenomena, 2008, 138: 385-392.

[15] WANG Xue-bin. Adiabatic shear localization for steels based on Johnson-Cook model and second- and fourth-order gradient plasticity models [J]. J Iron Steel Res, Int, 2007,14(5): 56-61.

[16] WANG Xue-bin. Quantitative calculation of local shear deformation in adiabatic shear band for Ti-6Al-4V [J]. Trans Nonferrous Met Soc China, 2007, 17(4): 698-704.

[17] WANG X B. Temperature-dependent shear strain localization of aluminum-lithium alloy in uniaxial compression using Zerilli-Armstrong and gradient plasticity models [J]. Mat Sci Forum, 2006, 519/521: 789-794.

[18] MARCHAND A, DUFFY J. An experimental study of the formation process of adiabatic shear bands in a structural steel [J]. J Mech Phys Solids, 1988, 36(3): 251-283.

[19] BATRA R C, KIM C H. Effect of thermal conductivity on the initiation, growth and bandwidth of adiabatic shear bands [J]. Int J Eng Sci, 1991, 29(8): 949-960.

[20] KLEPACZKO J R, REZAIG B. A numerical study of adiabatic shear banding in mild steel by dislocation mechanics based constitutive relations [J]. Mech Mat, 1996, 24(2): 125-139.

[21] ZHU H T, ZBIB H M. On the role of strain gradients in adiabatic shear banding [J]. Acta Mech, 1995, 111(1/2): 111-124.

[22] DODD B, BAI Y. Width of adiabatic shear bands [J]. Mat Sci Tech, 1985, 1(1): 38-40.

Foundation item: Project(2004F052) supported by the Educational Department of Liaoning Province, China

Corresponding author: WANG Xue-bin; Tel: +86-418-3350924; E-mail: wxbbb@263.net

(Edited by LI Xiang-qun)