Slip flow and variable properties of viscoelastic fluid past astretching surface embedded in a porous medium with heat generation
来源期刊:中南大学学报(英文版)2016年第4期
论文作者:Ahmed M. Megahed
文章页码:991 - 999
Key words:viscoelastic fluid; variable fluid properties; slip velocity
Abstract: This study examines theoretically and computationally the non-Newtonian boundary layer flow and heat transfer for a viscoelastic fluid over a stretching continuous sheet embedded in a porous medium with variable fluid properties, slip velocity, and internal heat generation/absorption. The flow in boundary layer is considered to be generated solely by the stretching of the sheet adjacent to porous medium with boundary wall slip condition. Highly nonlinear momentum and thermal boundary layer equations governing the flow and heat transfer are reduced to set of nonlinear ordinary differential equations by appropriate transformation. The resulting ODEs are successfully solved numerically with the help of shooting method. Graphical results are shown for non-dimensional velocities and temperature. The effects of heat generation/absorption parameter, the porous parameter, the viscoelastic parameter, velocity slip parameter, variable thermal conductivity and the Prandtl number on the flow and temperature profiles are presented. Moreover, the local skin-friction coefficient and Nusselt number are presented. Comparison of numerical results is made with the earlier published results under limiting cases.
J. Cent. South Univ. (2016) 23: 991-999
DOI: 10.1007/s11771-016-3147-4

Ahmed M. Megahed
Department of Mathematics, Faculty of Science, Benha University (13518), Egypt
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: This study examines theoretically and computationally the non-Newtonian boundary layer flow and heat transfer for a viscoelastic fluid over a stretching continuous sheet embedded in a porous medium with variable fluid properties, slip velocity, and internal heat generation/absorption. The flow in boundary layer is considered to be generated solely by the stretching of the sheet adjacent to porous medium with boundary wall slip condition. Highly nonlinear momentum and thermal boundary layer equations governing the flow and heat transfer are reduced to set of nonlinear ordinary differential equations by appropriate transformation. The resulting ODEs are successfully solved numerically with the help of shooting method. Graphical results are shown for non-dimensional velocities and temperature. The effects of heat generation/absorption parameter, the porous parameter, the viscoelastic parameter, velocity slip parameter, variable thermal conductivity and the Prandtl number on the flow and temperature profiles are presented. Moreover, the local skin-friction coefficient and Nusselt number are presented. Comparison of numerical results is made with the earlier published results under limiting cases.
Key words: viscoelastic fluid; variable fluid properties; slip velocity
1 Introduction
There is considerable interest among recent researchers in the boundary layer flow problems over a stretching surface. Such problems occur in several manufacturing processes, such as continuous cooling and fibers spinning, polymer extrusion, wire and fiber coating, foodstuff processing, paper production, hot rolling, solidification of liquid crystals, petroleum production, exotic lubricants and suspension solutions. Due to the importance of this work, further considerations have been carried out both experimentally and theoretically in this field of research. Crane [1] was the first one who obtained an elegant analytical solution to the boundary layer equations for the steady two-dimensional flow due to a stretching surface in a quiescent incompressible fluid taking into account the case of a linearly stretched surface. The problem of Newtonian flow past a stretching surface has been extended in various ways [2-12]. Therefore, the significance of the results reported in the above works is limited because it concerns only with Newtonian fluid. In a general sense, fluids that exhibit characters not predicted by the Newtonian constitutive equation are non-Newtonian. The so-called non- Newtonian fluids are often found in many fields of engineering fluid mechanics as well as in bio-medical fields, and exhibit interesting, useful and even exciting characteristics different from those found in Newtonian fluids. So, there is a continuing interest in understanding the properties of non-Newtonian fluids especially the viscoelastic type. This type of fluid possesses both viscous and elastic properties; bitumen, nylon and flour dough are examples. The interest of flow in viscoelastic fluid is getting more and more attention and growing up to be an important research area because of its industrial manufacturing processes, such as manufacturing of foods and papers, manufacturing process of artificial film and artificial fibers. Likewise, the non-Newtonian viscoelastic fluid has another important application involving atomization such as paints, inks, coating, jet fuels and possible to reduce frictional drag on the hulls of ships and submarines. Due to the high applicability of non-Newtonian viscoelastic fluids in such industrial phenomena, it has attracted the attentions of many researchers. For instance, Rajagopal et al [13] presented a study of the flow of an incompressible non- Newtonian viscoelastic fluid past a stretching sheet. Vajravelu and Rollins [14] have studied the flow and heat transfer of an incompressible viscoelastic fluid due to stretching of a plane elastic surface in the approximation of boundary layer theory. They have examined the effects of viscous dissipation and internal heat generation or absorption in a viscoelastic boundary layer flow. Also, to get a better control on the rate of heat exchange, in recent years it has been proposed to employ the fluids which are more viscoelastic in nature than viscous such as water with polymeric additives [15]. By using such additives the viscosity of the fluid increases and it slows down the rate of solidification. Sarma and Nageswara RAO [16] investigated the analytical solution for the laminar steady flow and heat transfer problem of an incompressible viscoelastic fluid past a semi-infinite stretching sheet under the effects of viscous dissipation and internal heat generation/absorption. The problem for viscoelastic fluid flow and heat transfer in a porous medium over a stretching sheet studied by Subhas and Veena [17]. Sanjayanand and Khan [18] analyzed the problem of flow, heat and mass transfers in a viscoelastic boundary layer fluid over an exponentially stretching continuous sheet in the presence of viscous dissipation and elastic deformation. Nandeppanavar et al [19] investigated the effects of viscous dissipation on the flow and heat transfer of a viscoelastic fluid flow in porous medium over a stretching sheet surface.
In all the above-mentioned studies the slip velocity effect is negligible. However, the velocity slip effect is interesting macroscopically physical phenomenon in fluid mechanics. This phenomenon is also known as the non-adherence of the fluid to a solid boundary which has been observed under certain circumstances. For example, polymer melts often exhibit macroscopic wall slip which in general is governed by a nonlinear and monotone relation between the slip velocity and the traction. Experimental results [20] have shown that the empirical non-slip boundary condition may break down depending on the fluid properties and interfacial roughness. Therefore, the slip effect should be taken into account, which leads to the requirement of a slip boundary condition. The earliest slip boundary condition was proposed by Navier [21]. He showed a linear relationship between the slip velocity and the shear rate at the wall. But according to the results from molecular dynamics simulations, Thompson and Troian [22] discovered that the slip velocity is related to the slip length, the shear rate at the wall and a critical shear rate at which the slip length diverges. Wall slip readily occurs for an array of complex fluid such as emulsions, suspensions, foams, and polymer solutions. Also, the fluids that exhibit boundary slip have important technological applications such as in the polishing of artificial heart valves and internal cavities. Turkyilmazoglu [23] investigated the MHD slip flow of an electrically conducting, viscoelastic fluid past a stretching surface. Recently, Megahed [24] investigated the numerical solution for the slip velocity and variable viscosity effects on the flow and heat transfer of a non-Newtonian power-law fluid over a stretching surface in the presence of thermal radiation and constant heat flux. Very recently, El-Hawary et al [25] examined the effect of slip velocity, concentration dependent diffusivity, thermal convective boundary conditions, and heat source/sink on the stagnation-point heat and mass transfer of a viscoelastic fluid over a stretching sheet using Lie group analysis.
All the above studies are carried out for the fluids having constant physical properties through the flow regime but practical situations demand for physical properties with variable characteristics. Thermal conductivity is one of such properties. However, it is known that the physical property may change significantly with temperature. Also, the prediction of heat transfer characteristics for the non-Newtonian viscoelastic fluids with variable properties in porous media is very important due to its practical engineering applications, such as oil recovery, geothermal energy recovery, ground water pollution, thermal energy storage, flow through filtering media and food processing. So, the purpose of the present work is to investigate the numerical solution for the variable fluid properties, internal heat generation/absorption and velocity slip effects on the flow and heat transfer of a non-Newtonian viscoelastic fluid over a permeable stretching surface embedded in porous medium.
2 Mathematical formulation
Consider a steady, two-dimensional boundary layer flow of an incompressible non-Newtonian viscoelastic fluid over a stretching sheet embedded in a porous medium with internal heat generation/absorption and velocity slip effects. The origin is located at a slit, through which the sheet (see Fig. 1.) is drawn through the fluid medium. The x-axis is chosen along the sheet and y-axis is taken normal to it.

Fig. 1 Flow geometry and coordinate system
The continuous stretching sheet is assumed to have the velocity U=cx where x is the coordinate measured along the stretching surface and c>0 is a constant for a stretching sheet and temperature distribution for the sheet is assumed to take the form 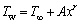 where Tw is the temperature of the sheet,
where Tw is the temperature of the sheet,  is the temperature of the fluid far away from the sheet, A and r are constants.
is the temperature of the fluid far away from the sheet, A and r are constants.
Making the usual boundary layer approximations for the non-Newtonian viscoelastic fluid, the steady two-dimensional boundary-layer equations taking into account the internal heat generation/ absorption and velocity slip effects can be written as
 (1)
(1)
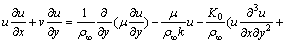
 (2)
(2)
 (3)
(3)
where u and v are the velocity components in the x and y directions, respectively;  is the density of the fluid away from the surface;
is the density of the fluid away from the surface; 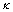 the fluid thermal conductivity; K0 is a positive parameter associated with the viscoelastic fluid; T is the temperature of the fluid; μ is the fluid viscosity; k is the permeability of the porous medium; Q0 is the heat generation/absorption coefficient; cp is the specific heat capacity at constant pressure.
the fluid thermal conductivity; K0 is a positive parameter associated with the viscoelastic fluid; T is the temperature of the fluid; μ is the fluid viscosity; k is the permeability of the porous medium; Q0 is the heat generation/absorption coefficient; cp is the specific heat capacity at constant pressure.
The boundary conditions can be written as
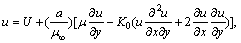
 (4)
(4)
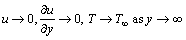 (5)
(5)
where a is the slip factor with dimension of length. The mathematical analysis of the problem is simplified by introducing the following dimensionless coordinates:
 (6)
(6)
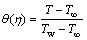 (7)
(7)
where η is the similarity variable; f(η) is the dimensionless stream function; 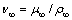 is the kinematic viscosity away from the surface; and θ(η) is the dimensionless temperature.
is the kinematic viscosity away from the surface; and θ(η) is the dimensionless temperature.
In this study, the fluid viscosity is assumed to vary as an exponential function of temperature in the form as [26]
 (8)
(8)
where k1 is a constant with the dimension of T-1; 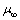 is the viscosity of the fluid away from the sheet so that eq. (8) may be written as
is the viscosity of the fluid away from the sheet so that eq. (8) may be written as
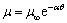 (9)
(9)
where  α is the dimensionless viscosity parameter depending on the nature of the fluid with α>0 for liquid and α<0 for gases.
α is the dimensionless viscosity parameter depending on the nature of the fluid with α>0 for liquid and α<0 for gases.
Also, the thermal conductivity κ is assumed to vary linearly with temperature [26] and it is of the form as
 (10)
(10)
where 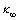 is the thermal conductivity away from the surface and ε is the thermal conductivity parameter.
is the thermal conductivity away from the surface and ε is the thermal conductivity parameter.
Therefore, upon using these variables, the boundary layer governing eqs. (2)-(3) can be written in a non-dimensional form as
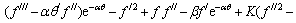
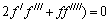 (11)
(11)
 (12)
(12)
the boundary conditions become:
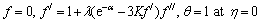 (13)
(13)
 (14)
(14)
where  is the porous parameter;
is the porous parameter; 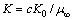 is the viscoelastic parameter;
is the viscoelastic parameter;  is the Prandtl number;
is the Prandtl number;  is the heat generation parameter (>0) or the absorption parameter (<0) and
is the heat generation parameter (>0) or the absorption parameter (<0) and  is the velocity slip parameter.
is the velocity slip parameter.
The physical quantities of primary interest are the local skin-friction coefficient Cfx and the local Nusselt number Nux which are defined as
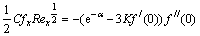 (15)
(15)
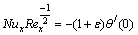 (16)
(16)
where  is the local Reynolds number.
is the local Reynolds number.
3 Analytical solution for momentum and energy equations
In this section, we observe that in the case of α=λ=0, Eq. (11) subject to the boundary conditions of Eqs. (13) and (14) has an exact solution in the following form as
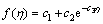 (17)
(17)
where c1, c2 and c3 are constants with c3>0. Substituting the relation Eq. (17) into Eq. (13) we obtain
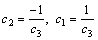 (18)
(18)
Substituting the assumed solution into Eq. (11) yields:
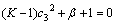 (19)
(19)
so, the closed form analytical solution reduces to
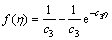 (20)
(20)
Hence,
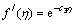 (21)
(21)
and
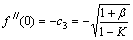 (22)
(22)
The exact solution for the energy equation (12) can be determined in the case of ε=0 and r=2. So, we can introduce a new variable ζ as
 (23)
(23)
Introducing Eqs. (20) and (23) into Eq. (12), we have
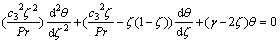 (24)
(24)
with the boundary conditions:
 (25)
(25)
The solution of Eq. (24) satisfying the boundary conditions (25) in terms of Kummer’s function F1(a, b, ζ) is
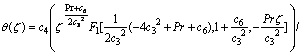
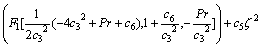 (26)
(26)
where 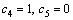 and
and 
The solution of Eq. (26) in terms of the variable η is

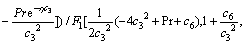
 (27)
(27)
4 Solution procedure using shooting method
The numerical procedure used to solve the differential system Eqs. (11)-(12). This system along with the boundary conditions Eqs. (13)-(14), is integrated numerically by means of Runge-Kutta method with systematic estimate of  and
and 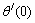 by Newton-Raphson shooting technique until the boundary conditions at the infinity
by Newton-Raphson shooting technique until the boundary conditions at the infinity  and
and  decay exponentially to zero. In this method it is necessary to choose a suitable finite value for
decay exponentially to zero. In this method it is necessary to choose a suitable finite value for 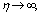 say
say  The following first-order system is set.
The following first-order system is set.
 (28)
(28)
Equations (11) and (12) with the boundary conditions (13) and (14) are then reduced to a system of a first-order ordinary differential equations, i.e.
 (29)
(29)
The shooting method is used to guess ε1 and ε2 by iterations until the outer boundary conditions 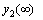 and
and 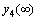 are satisfied. The resulting differential equations can be integrated by Runge-Kutta fourth order integration scheme. The above procedure is repeated until we get the results up to the desired degree of accuracy, 10-5.
are satisfied. The resulting differential equations can be integrated by Runge-Kutta fourth order integration scheme. The above procedure is repeated until we get the results up to the desired degree of accuracy, 10-5.
5 Validation of proposed method
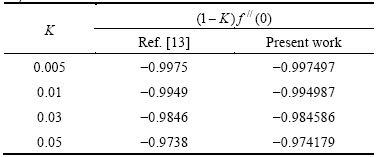
The validation of shooting method has been presented in Table 1 by comparing local skin-friction coefficient in terms of  when α=β=λ=0 for different values of viscoelastic parameter K with theearlier problem of Rajagopal et al [13]. From this comparison and without any doubt, from this table, we can claim that our results are in excellent agreement with this reference. Also, the obtained results demonstrate reliability and efficiency of the proposed method.
when α=β=λ=0 for different values of viscoelastic parameter K with theearlier problem of Rajagopal et al [13]. From this comparison and without any doubt, from this table, we can claim that our results are in excellent agreement with this reference. Also, the obtained results demonstrate reliability and efficiency of the proposed method.
Table 1 Values of 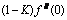 for various values of K with α=β=λ=0
for various values of K with α=β=λ=0
6 Results and discussion
This section aims to describe the behavior of parameters governing the flow and heat transfer involved in the momentum and energy equations. Thus, Figs. 2-12 are plotted. Figures 2-3 depict the influence of the porous parameter on the velocity and the temperature profiles, respectively. Figure 2 shows that the velocity decreases when the porous parameter β increases. It should be noted that greater values of β correspond to a high dynamic viscosity due to porous medium μ∞ and a small permeability for the porous medium which causes a production for more resistance to the fluid flow. This causes the velocity distribution to decrease when β increases as we can observe from Fig. 2 and so enhances the temperature distribution along the thermal boundary layer as we can see from Fig. 3. Also, from these figures we can observe that, owing to the increase in the value of the porous parameter, and as a result, the thermal boundary layer becomes thicker but the momentum boundary layer becomes thinner.
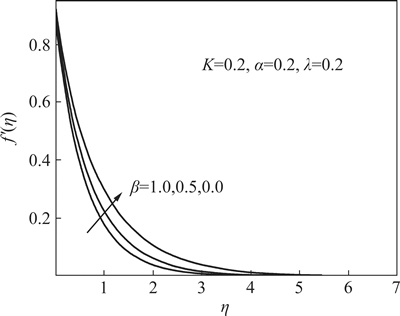
Fig. 2 behavior of velocity distribution for various values of β
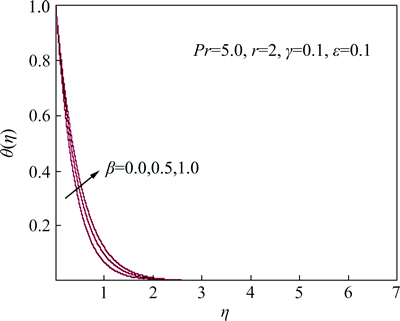
Fig. 3 behavior of temperature distribution for various values of β
Figures 4 and 5 elucidate the effects of the velocity slip parameter on the dimensionless velocity and temperature profiles, respectively. It is clear from these figures that the velocity decreases with the increase of the velocity slip parameter, while the temperature is increased with the increase of the slip parameter. Physically, as the slip parameter increases in magnitude, a creation is caused for the friction force which permits more fluid to slip past the sheet, and then the flow slows down for distance close to the sheet and the temperature rise due to the presence for this force.
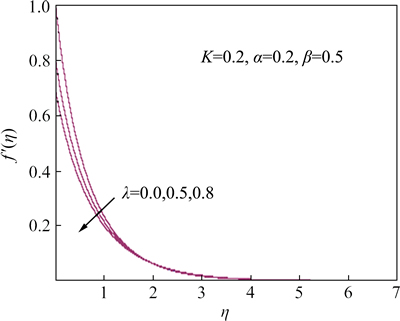
Fig. 4 behavior of velocity distribution for various values of λ
Figures 6 and 7, depict the variation of viscoelastic parameter K on the velocity distribution and temperature distribution, respectively. It is shown that the flow velocity decreases for increasing values of viscoelastic parameter away from the sheet while the temperature increases for increasing the same parameter but the effect is very weak on the temperature distribution. Physically, as the viscoelastic parameter increases, there exists a resistance for the velocity. As a result, the velocity and the boundary layer thickness decrease. On the other hand, the thermal boundary layer thickness increases with an increase in the viscoelastic parameter.

Fig. 5 behavior of temperature distribution for various values of λ

Fig. 6 behavior of velocity distribution for various values of K

Fig. 7 behavior of temperature distribution for various values of K
Figure 8 shows the effect of Prandtl number on the temperature profiles above the sheet. It is noticed that the larger Prandtl number has a lower thermal diffusivity. Therefore, a rapid increase in the Prandtl number Pr decreases the temperature and the thermal boundary layer thickness. This is because the fluid with higher value of Pr posses a large heat capacity, and hence intensifies the heat transfer.
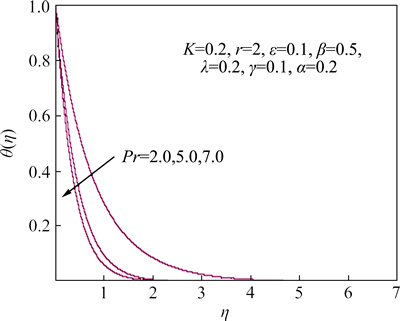
Fig. 8 behavior of temperature distribution for various values of Pr
Figure 9 illustrates that how profiles of temperature distribution are affected by the variations in the heat generation/absorption parameter γ when other parameters remain fixed. This figure indicates that the thermal boundary-layer thicknesses increase when the internal heat generation parameter γ>0 becomes stronger whereas the internal heat absorption parameter γ<0 has the opposite effect. Also, it is noticed that the highest temperature distribution for the fluid in the boundary layer was obtained with the greatest heat generation parameter γ>0. Likewise, it is shown that the effect of heat absorption parameter γ<0 causes a drop in the temperature distribution as the heat following from the sheet is absorbed. On the other hand, as can be expected an increase in the heat generation parameters will produce a decrease in the rate of heat transfer but the opposite effect is observed for the heat absorption parameters.
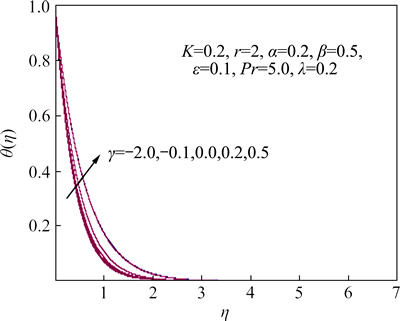
Fig. 9 behavior of temperature distribution for various values of γ
In addition, from Fig. 10 one can see the effect of thermal conductivity parameter on the temperature distribution. One can see from this figure that the thermal conductivity parameter has a relevant effect on the temperature distributions above the sheet. In fact, an increase in the thermal conductivity parameter appears to increase both the thermal boundary layer thickness and the temperature distributions. This means a lower temperature gradient at the wall with a subsequent drop in both the heat flux and the rate of cooling.
On the other hand, Fig. 11 depicts the velocity profiles for several values of viscosity parameter α. It is seen that the velocity away from the sheet decreases with the increase of viscosity parameter and this implies an accompanying reduction of the thickness of the momentum boundary layer; but along the sheet, fluid velocity increases with increasing the viscosity parameter.
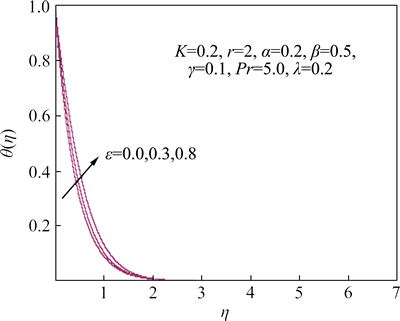
Fig. 10 behavior of temperature distribution for various values of ε

Fig. 11 behavior of velocity distribution for various values of α
Figure 12 shows the effects of the viscosity parameter on the temperature distribution. It is noticed that the temperature at a particular point is found to increase significantly with increasing the viscosity parameter. The rate of heat transfer (from the sheet to the fluid) decreases with increasing the viscosity parameter. As the viscosity parameter increases, less heat is transferred from the sheet to the fluid. It is important to note that the rate of cooling is much faster for smaller values of the viscosity parameter.
At this stage, Table 2 is presented in order to more fully characterize the behavior of the quantities of relevant physical interest like the local skin-friction coefficient 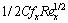 and the local Nusselt number
and the local Nusselt number  with changes in the porous parameter β, heat generation/absorption parameter γ, the velocity slip parameter λ, thermal conductivity parameter ε, viscoelastic parameter K, viscosity parameter α and the Prandtl number Pr. One can then see from Table 2 that, the effect of increasing values of porous parameter and velocity slip parameter is to boost the values of skin-friction coefficient and depress the local Nusselt number. Analysis of the tabular results shows that increase in the Prandtl number leads to an increase in both the local skin-friction coefficient and the local Nusselt number. This is because a fluid with larger Prandtl number possesses larger heat capacity, and hence intensifies the heat transfer. Likewise, both the local Nusselt number and the skin-friction coefficient are reduced with increasing for the thermal conductivity parameter. Also, it is observed that the increase in the viscoelastic parameter leads to a decrease in both the local skin-friction coefficient and the local Nusselt number. Physically, with decreasing friction, the heat generated on the surface transferred to the flow is reduced. This leads to a decrease in the rate of heat transfer. Also, a drop in skin-friction with an increase in the viscoelastic parameter as investigated in this work has an important implication that in free coating operations, elastic properties of the coating formulations may be beneficial for the whole process. On the other hand, as it is observed from this study, both the skin- friction coefficient and the local Nusselt number are decreased with increasing the heat generation parameter γ>0. Also, it is observed that both the local Nusselt number and the skin-friction coefficient are enhancing with increasing the heat absorption parameter γ<0. Finally, it is noticed from this table that the effect of increasing the values of viscosity parameter is to decrease both the skin-friction coefficient and local Nusselt number.
with changes in the porous parameter β, heat generation/absorption parameter γ, the velocity slip parameter λ, thermal conductivity parameter ε, viscoelastic parameter K, viscosity parameter α and the Prandtl number Pr. One can then see from Table 2 that, the effect of increasing values of porous parameter and velocity slip parameter is to boost the values of skin-friction coefficient and depress the local Nusselt number. Analysis of the tabular results shows that increase in the Prandtl number leads to an increase in both the local skin-friction coefficient and the local Nusselt number. This is because a fluid with larger Prandtl number possesses larger heat capacity, and hence intensifies the heat transfer. Likewise, both the local Nusselt number and the skin-friction coefficient are reduced with increasing for the thermal conductivity parameter. Also, it is observed that the increase in the viscoelastic parameter leads to a decrease in both the local skin-friction coefficient and the local Nusselt number. Physically, with decreasing friction, the heat generated on the surface transferred to the flow is reduced. This leads to a decrease in the rate of heat transfer. Also, a drop in skin-friction with an increase in the viscoelastic parameter as investigated in this work has an important implication that in free coating operations, elastic properties of the coating formulations may be beneficial for the whole process. On the other hand, as it is observed from this study, both the skin- friction coefficient and the local Nusselt number are decreased with increasing the heat generation parameter γ>0. Also, it is observed that both the local Nusselt number and the skin-friction coefficient are enhancing with increasing the heat absorption parameter γ<0. Finally, it is noticed from this table that the effect of increasing the values of viscosity parameter is to decrease both the skin-friction coefficient and local Nusselt number.

Fig. 12 behavior of temperature distribution for various values of α
Table 2 Values of  and
and 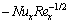 for various values of
for various values of  and α
and α
7 Conclusions
The problem presented deals with the effects of internal heat generation/absorption and slip velocity on the flow and heat transfer of a viscous non-Newtonian viscoelastic fluid over a stretching sheet which is embedded in a porous medium with variable fluid thermal properties. An exact analytical solution is obtained for the case of no slip condition and in the constant fluid properties. The governing equations for the flow and temperature fields are reduced to a system of coupled nonlinear ordinary differential equations. These nonlinear differential equations are then solved numerically via the shooting technique involving Runge-Kutta integration scheme together with Newton-Raphson method. The numerical results are verified with the earlier study by Rajagopal [13] and found to be in good agreement. Important findings of our analysis obtained are listed below:
1) The rate of heat transfer increases with an increase in Prandtl number and heat absorption parameter. Thus fast cooling of the stretching sheet can be achieved by implementing these effects.
2) The effect of increasing values of the porous parameter or the slip parameter is to enhance the local skin-friction coefficient.
3) The effects of increasing the values of the viscosity parameter, thermal conductivity parameter and heat generation parameter are to decrease the local Nusselt number.
4) Moreover, a large value of the viscoelastic parameter and the viscosity parameter lead to a decrease in the value of the skin-friction coefficient.
Acknowledgements
The author is very grateful to the editor and referees for carefully reading the paper and for their comments and suggestions which have improved the paper. Also, the author would like to express his sincere thanks to Professor Mostafa A A Mahmoud for his valuable suggestions.
References
[1] CRANE L J. Flow past a stretching plate [J]. Z Angew Math Physk, 1970, 21: 645-647.
[2] GUPTA P S, GUPTA A S. Heat and mass transfer on a stretching sheet with suction and blowing [J]. The Canadian Journal of Chemical Engineering, 1977, 55: 744-746.
[3] CARRAGHER P, CRANE L J. Heat transfer on a continuous stretching sheet [J]. Zeitschrift fur angewandte Mathematik und Mechanik, 1982, 62: 564-565.
[4] POP I, NA T Y. A note on MHD flow over a stretching permeable surface [J]. Mechanics Research Communications, 1988, 25: 263-269.
[5] VAJRAVELU K, NAYFEH J. Convective heat transfer at a stretching sheet [J]. Acta Mechanica, 1993, 96: 1227-1235.
[6] ALI M E. Heat transfer characteristics of a continuous stretching surface [J]. Warme-Stoffubertrag, 1994, 29: 227-234.
[7] ALI M E. On thermal boundary layer on a power law stretched surface with suction or injection [J]. International Journal Heat and Mass Flow, 1995, 16: 280-290.
[8] KUMARAN V, RAMANAIAH G. A note on the flow over a stretching sheet [J]. Acta Mechanica, 1996, 116: 229-233.
[9] MAHAPATRA T R, GUPTA A S. Stagnation-point flow towards a stretching surface [J]. The Canadian Journal of Chemical Engineering, 2003, 81: 258-263.
[10] MAHMOUD M A A, MEGAHED A M. Effect of suction and injection on MHD heat transfer in an electrically conducting fluid at a stretching vertical plate embedded in a porous medium with uniform free stream [J]. Il Nuovo Cimento B, 2006, 121: 923-935.
[11] CORTELL R. Viscous flow and heat transfer over a nonlinearly stretching sheet [J]. Applied Mathematics and Computation, 2007, 184: 864-873.
[12] ABDEL-RAHMAN REDA G, MEGAHED A M. Lie group analysis for a mixed convective flow and heat mass transfer over a permeable stretching surface with Soret and Dufour effects [J]. Journal of Mechanics, 2014, 30: 67-75.
[13] RAJAGOPAL K R, NA T Y, GUPTA A S. Flow of a viscoelastic fluid over a stretching sheet [J]. Rheologica Acta, 1984, 23: 213-215.
[14] VAJRAVELU K, ROLLINS D. Heat transfer in a viscoelastic fluid over a stretching sheet [J]. Journal of Mathematical Analysis and Applications, 1991, 158: 241-255.
[15] ANDERSSON H I. MHD flow of a viscoelastic fluid past a stretching surface [J]. Acta Mechanica, 1992, 95: 227-230.
[16] SARMA M S, NAGESWARA RAO B. Heat transfer in a viscoelastic fluid over a stretching sheet [J]. Journal of Mathematical Analysis and Applications, 1998, 222: 268-275.
[17] SUBHAS A, VEENA P. Viscoelastic fluid flow and heat transfer in a porous medium over a stretching sheet [J]. International Journal of Nonlinear Mechanics, 1998, 33: 531-540.
[18] SANJAYANAND E, KHAN S K. On heat and mass transfer in a viscoelastic boundary layer flow over an exponentially stretching sheet [J]. International Journal of Thermal Sciences, 2006, 45: 819-828.
[19] NANDEPPANAVAR M M, ABEL M S, VAJRAVELU K. Flow and heat transfer characteristics of a viscoelastic fluid in a porous medium over an impermeable stretching sheet with viscous dissipation [J]. International Journal of Heat Mass Transfer, 2010, 53: 4707-4713.
[20] COTTIN-BIZONNE C, CROSS B, STEINBERGER A, CHARLAIX E. Boundary slip on smooth hydrophobic surfaces: intrinsic effects and possible artifacts [J]. Physical Review Letters, 2005, 94: 056-102.
[21] NAVIER C L M H. Memory on the laws of motion of fluids [J]. Memoires Académie des Sciences Institut de France, 1823, 6: 389-416. (in French)
[22] THOMPSON P A, TROIAN S M. A general boundary condition for liquid flow at solid surfaces [J]. Nature, 1997, 389: 360-362.
[23] TURKYILMAZOGLU M. Multiple solutions of heat and mass transfer of MHD slip flow for the viscoelastic fluid over a stretching sheet [J]. International Journal of Thermal Sciences, 2011, 50: 2264-2276.
[24] MEGAHED A M. Variable viscosity and slip velocity effects on the flow and heat transfer of a power-law fluid over a non-linearly stretching surface with heat flux and thermal radiation [J]. Rheologica Acta, 2012, 51: 841-847.
[25] EL-HAWARY H M, MOSTAFA A A MAHMOUD, ABDEL- RAHMAN REDA G, ABEER S E. Similarity analysis for effects of variable diffusivity and heat generation/absorption on heat and mass transfer for a MHD stagnation-point flow of a convective viscoelastic fluid over a stretching sheet with a slip velocity [J]. Mathematical Problems in Engineering, 2013: 1-11.
[26] MOSTAFA A A M. The effects of variable fluid properties on MHD Maxwell fluids over a stretching surface in the presence of heat generation/absorption [J]. Chemical Engineering Communications, 2011, 198: 131-146.
(Edited by YANG Hua)
Received date: 2015-04-07; Accepted date: 2015-06-21
Corresponding author: Ahmed M. Megahed, PhD; Tel: +2-01141387632; E-mails: ah_mg_sh@yahoo.com, ahmed.abdelbaqk@fsc.bu.edu.eg

