J. Cent. South Univ. (2012) 19: 357-364
DOI: 10.1007/s11771-012-1012-7
Optimization of rotor shape for constant torque improvement and radial magnetic force minimization
CHO Gyu-won, WOO Seok-hyun, JI Seung-hun, PARK Kyoung-won, JANG Ki-bong, KIM Gyu-tak
School of Mechatronics, Changwon National University, Changwon 641-773, Korea
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: The design of notch and barrier was optimized in order to improve the characteristics of constant torque while minimizing the cogging torque that occurs as a result of teeth and slot structure. The barrier was installed in order to minimize the cogging torque and torque ripple by finite element method (FEM) with a reduced barrier width toward the center of magnetic pole. The position and width of notch, which can offset cogging torque, can be calculated with energy distribution of air-gap using Fourier series. The optimized model demonstrates a 60% decrease in the cogging torque, a 75.3% decrease in the torque ripple and a 3% increase in the operating torque when compared with the basic model.
Key words: permanent magnet synchronous motor; barrier; notch; radial magnetic force; cogging torque
1 Introduction
An interior permanent magnet synchronous motor (IPMSM) is a mechanically strong structure with permanent magnets embedded in rotor, and the generating torque per unit volume is greater than that of surface permanent magnet synchronous motor (SPMSM) because the reluctance torque brought by a inductance difference between d-axis and q-axis is combined with the magnetic torque. In addition, IPMSM can be the fastening permanent magnet, so it can be used as an operating motor of precision equipment in case of the automotive electronics which requires suddenly decelerating operation and wide range of speed control [1-2]. However, IPMSM has disadvantages that local flux saturation is generated due to inserting permanent magnet into the rotor. Also, cogging torque is greater than that of SPMSM because of the large magnetic flux density caused by a small effective air-gap. Therefore, the vibration and noise occur when motor is operating [3-4]. The occurrence of these large vibration and noise makes the distortion of the current and can be a reason of malfunction in motor driving systems [5-6]. To decrease cogging torque and torque ripple, many solutions were proposed by changing stator shape and slot opening, but these are not effective methods to decrease cogging torque and torque ripple [7-10]. Therefore, to decrease cogging torque and operating torque ripple, notch and barrier on the rotor were installed in this work. Also, the optimized design was carried out by design of experiment and various characteristics including torque were studied by finite element method (FEM). In addition, in order to verify resonance frequency, natural frequency of the stator was analyzed by modal analysis and proved by experiment.
2 Generated torque
2.1 Model design and specifications
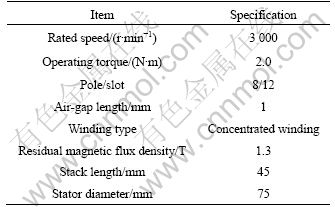
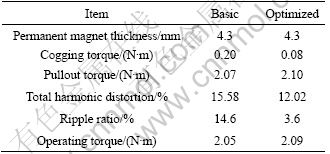
The basic model specifications are listed in Table 1. The cogging torque is significant in comparison with the operating torque, thus the optimization of rotor shape is performed during a rated operation, which is able to decrease the cogging torque and maintain the operating torque.
Table 1 Specification of basic model
2.2 Shape optimization
In this work, in order to improve the characteristics of the operating torque through the reduction of the cogging torque, a barrier and notch were installed. The optimization was performed through the experiment design and FEM analysis. The objective function was a minimization of the cogging torque while the operating torque was limited. The barrier model is a method of reducing the torque ripple using the sinusoidal distribution of the flux caused by the permanent magnet in the air-gap, which results in the flux density to be smaller toward the permanent q-axis by the d-axis standard [11]. By installing a barrier, the partial demagnetization was removed and the cogging torque was decreased. The location was set as a structure at both ends of the permanent magnet toward the center.
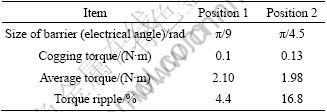
Figure 1 shows the barrier locations. The barrier was installed in order to minimize the cogging torque and torque ripple by FEM with a reduced barrier width toward the center of magnetic pole. Table 2 gives a comparison of the operating characteristics according to the barrier location. When the barrier was increased at Position 2 (as shown in Fig. 2), the average torque decreased and the torque ripple increased because the barrier interfered with not only the path of the flux leakage block, but also the main flux flow.
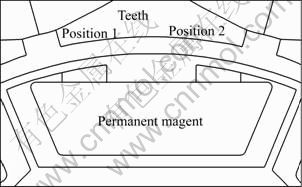
Fig. 1 Position of barrier
Table 2 Comparison of operating characteristics according to barrier location
The cogging torque is a irregular torque in a motor and force of the tangential direction which moves to a location where the magnetic energy is minimum. The position (α) and width (γ) of the notch, which can offset cogging torque, can be calculated with energy distribution of air-gap using Fourier series. Because cogging torque is generated by the irregular magnetic distribution on the rotor surface, in the case of slotless which changes permeance in the air-gap, the energy function according to the magnetization distribution is shown in Fig. 3.
 (1)
(1)
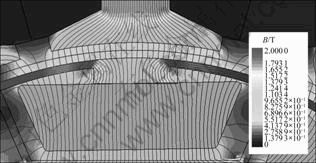
Fig. 2 Position 2 of flux distribution of barrier

Fig. 3 Equivalent magnetization distribution of base model
The cogging torque is presented as a harmonic wave during the motor operating, and it is multiples dividing the least common multiple of the number of permanent magnet poles and slots by poles. Therefore, the frequency of cogging torque formula is
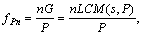 n=1, 2, 3, … (2)
n=1, 2, 3, … (2)
In order to reduce cogging torque of harmonic components shown as the above formula, notch which can change the distribution of the flux density shape is designed. Figure 4 shows the equivalent magnetization distribution of notch applied model.
When the width of the notch is 2γ and the position of the notch is α, the energy function according to the magnetic distribution of the permanent magnet is as follow:
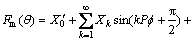
 (3)
(3)
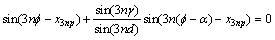 (4)
(4)
 k=0, 1, … (5)
k=0, 1, … (5)
 (6)
(6)
or
 k=0, 1, … (7)
k=0, 1, … (7)
 (8)
(8)
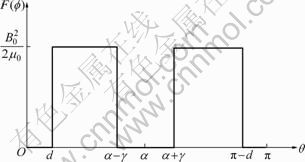
Fig. 4 Equivalent magnetization distribution of notch applied model
The position and width of notch were calculated by Fourier series [12-13]. Table 3 shows the result of harmonic components calculations. In the case of the eight-pole twelve- slot model, cogging torque was displayed as the 3n harmonics. However, when notch is solely installed and set after the installation of the barrier, the position is the same, but the width is changed. Because the notch width for reduction of 3n harmonics is influenced by cogging torque caused by barrier firstly, the optimized notch width is changed. Therefore, notch width has to be decided after installing the barrier and this is analyzed by FEM.
Table 3 Location of eight-pole twelve-slot model

Figure 5(a) shows the notch location. Model 1 is the optimized model that minimizes the cogging torque using only the installed notch. Model 2 optimized the barrier first and then applied the notch from Model 1. Model 3 is the optimized width of the notch after the barrier installation. The barrier locations of Model 2 and 3 are the same as that of Position 1. Table 4 gives the operating characteristics of each model. The cogging torque is largely decreased due to the reduction of the leakage flux and flux harmonics components in Model 2, as listed in Table 4. However, the flux flow was distorted due to a large air-gap at the notch, so the torque ripple is significantly increased. Thus, in order to reduce the cogging torque and improve the torque operating characteristics, the notch width must be optimized after the barrier installation, as shown in Model 3.
2.3 Analysis of operating characteristics
Figure 6 shows the cogging torque and operating torque characteristics of the basic model and the optimized Model 3. The cogging torque decreases due to the installation of the notch, yet the operating torque decreases due to the flux linkage reduction caused by an increase of the magnetic reluctance. Because the flux is sinusoidally distributed through the barrier installation, the operating torque increases. Thus, the overall operating characteristics are improved.
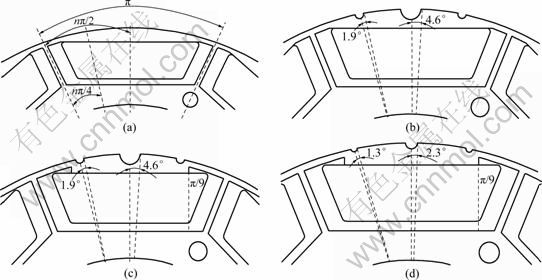
Fig. 5 Position and width of notch: (a) Position of notch; (b) Model 1; (c) Model 2; (d) Model 3
Table 4 Operating characteristics of different models
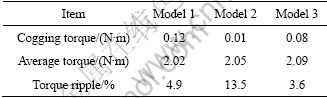
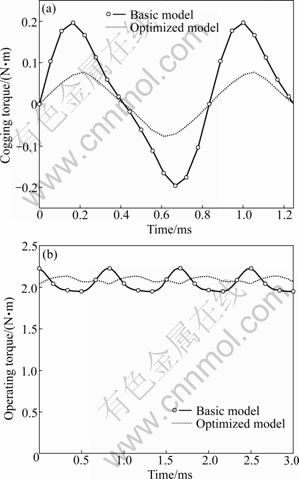
Fig. 6 Operating characteristics: (a) Cogging torque; (b) Operating torque
The model optimization with the application of the notch and barrier is demonstrated by a 60% decrease in the cogging torque, a 75.3% decrease in the torque ripple, and a 3% increase in the operating torque compared with the basic model. Thus, the operating characteristics are significantly improved. Table 5 compares characteristics of the basic model and optimized model.
Table 5 Operating characteristics of basic and optimization models
Equation (9) shows a frequency fc of cogging torque:
 (9)
(9)
where k is a constant; lcm is the smallest common multiple of pole and slot; Nm is the number of revolutions. The frequency of the cogging torque is 1 200 Hz at the rated speed.
3 Radial magnetic force
In electrical equipment, the cause of noise can be classified using electromagnetic factors, mechanical factors, and aerodynamic factors. Figure 7 shows the process where these causes are transmitted into the air through vibrations of each part [14].

Fig. 7 Origins of noise and vibration and their transfer process
In order to reduce the vibrations from the motor, a comprehensive analysis of the above three factors and the combination between the mechanical and electronic systems was implemented. Figure 8 shows the imbalances of air-gap. Because the electromagnetic vibration source operating in the motor is generated by the organic relationship between the electromagnetic and mechanical factors, as shown in Fig. 8, an eccentricity of air-gap caused by imbalance in the air-gap influences the vibration characteristic of the motor. The air-gap eccentricity can be classified as static eccentricity and dynamic eccentricity. These mechanical eccentricities cause the operating characteristics to degrade in the motor due to the creation of many harmonics in the flux density of air-gap, imbalances of the radial magnetic force (RMF) and worsening of the noise and vibration characteristics as a result of vibration force. Therefore, in order to decrease the vibration, the mechanical movement must be analyzed and the conditions of eccentricity must be predicted from the electromagnetic RMF [15-16]. In this work, the natural frequency of the stator and size of the resonance were compared through electromagnetic RMF calculations of each model.
3.1 Natural frequency analysis and measurement of basic model
Figure 9 shows the free vibration using FEM without RMF, namely the natural frequency of stator, and the mode shapes due to natural frequency are represented by the frequency of each mode.
A silicon steel plate (S60-50PN1650) whose mass density is 7 850 kg/m? is used as a material of stator, and the parameters of the elastic modulus and Poisson ratio are 200 GPa and 0.24, respectively. In process where the rotor pole pushed and pulled the end of the stator teeth, as shown in Fig. 10(a), a twisted mode occurred, as illustrated in Fig. 9(b). Also, for the force that was applied to the stator, as shown in Fig. 10(b), the radial direction modes occurred, as illustrated in Figs. 9(a) and (c).

Fig. 8 Radial magnetic force caused by inbalance of air-gap

Fig. 9 Mode shapes corresponding to natural frequencies: (a) 1 415 Hz; (b) 2 865 Hz; (c) 3 728 Hz; (d) 6 522 Hz
Figure 11 shows the motor and experimental devices which were used in the natural frequency experiment. The PV-97C was selected as an acceleration sensor, SA-01A-4 model was adopted as a signal analyzer, and a vibration signal was amplified by UV-06A amplifier.
Figure 12 shows the experimental results. The experiment of the one-phase excitation was performed while the motor was stopped, as shown in Fig. 12(a). Additionally, the voltage source was applied using a pulse wave in one-phase of three phases. Then, the vibration signal was measured in a radial direction that was impacted by an electromagnetic pulling force. In the three-phase excitation experiment, the vibration was measured when each phase was at the rated current, as shown in Fig. 12(b).
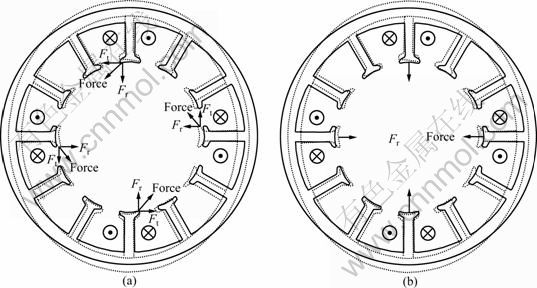
Fig. 10 Deformation of stator due to electromagnetic force: (a) Overlap position; (b) Aligned position

Fig. 11 Experimental device and motor: (a) Accelerometer; (b) Signal analyzer and DC supplier
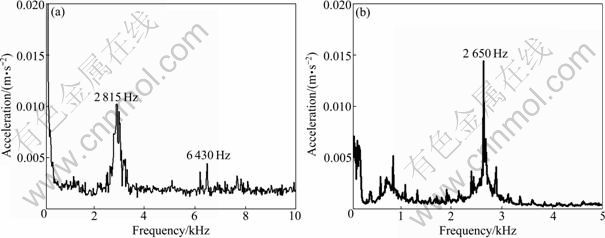
Fig. 12 Experimental results: (a) One-phase excitation; (b) Three-phase excitation
As a result, the vibration was generated at the lower frequency than the mode shown in Fig. 9(b). The reason is that the part of the frontier was different from the model of the analysis because the mounting of motor is installed on the frontier. Thus, satisfied results were obtained as the analysis value was relatively consistent with the experimental value.
The vibration due to the cogging torque is significantly reduced in the optimized model because the cogging torque was reduced by 30% compared with the basic model which has a fundamental frequency of 1 200 Hz of cogging torque.
3.2 Analysis of radial magnetic force
In previous analyses, it was difficult to compare the influence of the vibration according to the changes in the rotor shape because the influence of the rotor shape was not considered. The vibrations generated by the changes in the air-gap flux of the basic and optimized model were compared with the distribution and RMF conditions. The electromagnetic radial magnetic source is typically generated by the relation mechanical factor with the electromagnetic state. The resonance is generated when the frequency of electromagnetic vibration approaches the natural frequency of the motor. Thus, it not only causes the performance characteristics to decrease but also negatively influences other systems. Also, the wear and tear on the machine are very serious. The electromagnetic vibration source and noise are generated by the radial force density of the stator surface from the air-gap magnetic field in the open-circuit or on-load. The radial force density can be calculated using Maxwell’s stress tensor method as
 (10)
(10)
where Frad is the radial component of force density; Br and Bθ are the radial and tangential components of the air-gap flux density, respectively; μ0 is the permeability of free space; θs is the angular position; t is the time.
Figure 13 shows the radial force density of each model. Figure 14 shows the calculation and fast Fourier transform (FFT) of RMF to predict the electromagnetic radial source. The RMF is slightly increased due to the increase in the radial component of air gap flux. On the contrary, the harmonics of 1 200 Hz, which is relevant to the cogging torque frequency, is highly decreased. Thus, as a result of RMF analysis, the vibration will be extremely decreased by the huge reduction of RMF in the natural frequency band.
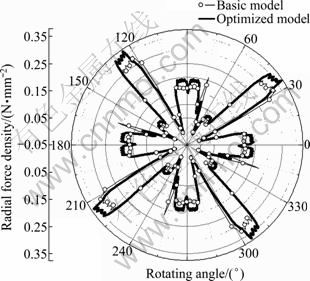
Fig. 13 Radial magnetic force
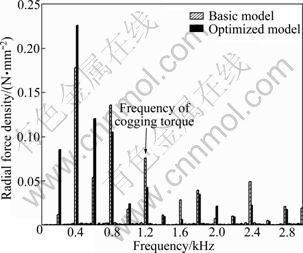
Fig. 14 Harmonic analysis of RMF
4 Conclusions
1) The optimal design of a notch and barrier is undertaken through DOE and FEM analyses. Various characteristics and RMFs are studied. The shape of the rotor is carried out by FEM. The operating characteristics are improved when the notch width is optimized after the optimal design of the barrier. The optimized model applied with notch and barrier is demonstrated by 60% decrease of cogging torque, 75.3% decrease of torque ripple and 3% increase of operating torque than basic model. So, operating characteristic is significantly improved.
2) Since the RMF is decreased by reduction of cogging torque, the resonance of cogging torque frequency and operating frequency will be decreased. To verify the resonance of frequency, the natural frequency is calculated through modal analysis and proven by experiment. Also, the RMF is slightly increased due to the increase in the radial component of air gap flux. On the contrary, the harmonics, which is relevant to the cogging torque frequency, is highly decreased. Thus, as a result of RMF analysis, the vibration will be extremely decreased by the huge reduction of the RMF in the natural frequency band.
References
[1] KO H S, KIM K J. Characterization of noise and vibration source in interior permanent-magnet brushless DC motors [J]. IEEE Transactions on Magnetics, 2004, 40(6): 3482-3489.
[2] KANG G H, SONG Y D, KIM G T, HUR J. A novel cogging torque reduction method for interior type permanent magnet motor [J]. IEEE Transactions on Industry Applications, 2009, 45(1): 161-167.
[3] JOHNS T M, SOONG W L. Pulsating torque minimization techniques for permanent magnet AC motor drives [J]. IEEE Transactions on Industry Applications, 1996, 43(2): 321-330.
[4] LEE S H, HONG J P, HWANG S M, LEE J Y, KIM Y K. Optimal design for noise reduction in interior permanent magnet motor [J]. IEEE Transactions on Industry Applications, 2006, 5: 1927-1932.
[5] EDE J D, ZHU Z Q, HOWE D. Rotor resonances of high-speed permanent-magnet brushless machine [J]. IEEE Transactions on Industry Applications, 2002, 38(6): 1542-1548.
[6] CAMERON D E, LANG J H, UMANS S D. The origin and reduction of acoustic noise in doubly salient variable reluctance motors [J]. IEEE Transactions on Industry Applications, 1992, 28(6): 1250-1255.
[7] KWAK J, MIN S, HONG J P. Optimal stator design of interior permanent magnet motor to reduce torque ripple using level set method [J]. IEEE Transactions on Magnetics, 2010, 46(6): 2108- 2111.
[8] LEE S H, HONG J P, HWANG S M. Optimal design for noise reduction in interior permanent-magnet motor [J]. IEEE Transactions on Industry Applications, 2009, 45(6): 1954-1960.
[9] KIOUMARSI A, MOALLEM M, FAHIMI B. Mitigation of torque ripple in interior permanent magnet motors by optimal shape design [J]. IEEE Transactions on Magnetics, 2006, 42(11): 3706-3711.
[10] THOMAS S S H, JAHNS T M, SOONG W L. Torque ripple reduction in interior permanent magnet synchronous machines using the principle of mutual harmonics exclusion [C]// Proceedings of Industry Applications Conference, 2007. 42nd IAS Annual Meeting. New Orleans, USA, 2007: 558-565.
[11] LEE J Y, LEE S H, LEE G H, HONG J P, HUR J. Determination of parameters considering magnetic nonliterary in an interior permanent magnet synchronous motor [J]. IEEE Transactions on Magnetics, 2006, 42(4): 1303-1306.
[12] KOH C S, SEOL J S. New cogging-torque reduction method for brushless permanent-magnet motor [J]. IEEE Transactions on Magnetics, 2003, 39(6): 3503-3506.
[13] WANG X, YANG Y, WANG D, DING T. Study of techniques for reducing the cogging torque in permanent magnet motors [C]// Proceedings for International Conference of Electrical machines and Systems (ICEMS 2008), China. 2008: 2899-2904.
[14] VIJAYRAGHAVAN P, KRISHNAN R. Noise in electric machines: A review [J]. IEEE Transactions on Industry Applications, 1999, 35(5): 1007-1013.
[15] DORRELL D G, THOMSON W T, ROACH S. Analysis of air gap flux, current, and vibration signals as a function of the combination of static and dynamic air gap eccentricity in 3phase induction motor [J]. IEEE Transactions on Industry Applications, 1997, 33(1): 24-34.
[16] ARKKIO A. Unbalanced magnetic pull in cage induction motors with asymmetry in rotor structures [C]// Proceedings of IEEE Conference Publication Proceedings of the International Conference on Electrical Machines and Drives. Cambridge, UK, 1997, 444: 36- 40.
(Edited by DENG Lü-xiang)
Foundation item: Research financially supported by Human Resource Training Project for Regional Innovation of Ministry of Education, Science and Technology (MEST) and National Research Foundation (NRF) and the Second Stage of Brain Korea 21 Projects, Korea
Received date: 2011-05-24; Accepted date: 2011-10-10
Corresponding author: KIM Gyu-tak, Professor, PhD; Tel: +82-55-213-3635; E-mail: gtkim@changwon.ac.kr