DOI：10.19476/j.ysxb.1004.0609.2018.11.17
纳米Cu薄膜摩擦的桥域多尺度模拟分析
桂军敏，倪玉山
(复旦大学 航空航天系，上海200433)
摘 要：为了研究纳米材料的微观变形过程，采用桥域方法(Bridging domain method)对纳米尺度下Cu薄膜表面摩擦过程进行模拟，得到摩擦阻力和系统变形能随摩擦距离的变化曲线，摩擦过程中存在静-动摩擦转化点。微观分析表明：摩擦初期Cu薄膜变形处于弹性阶段，随压头前方原子堆积，Cu薄膜进入塑性变形阶段，直接出现4层及以上原子的稳定滑移，同时薄膜内发射出沿非摩擦方向的斜向滑移带。以中心对称系数为度量捕捉到斜向滑移带内V形位错结构的产生与演化过程，确定V形位错的运动对摩擦塑性阶段的变形释放起主导作用。此外，对位错原子数目的统计分析表明，宏观下薄膜表面摩擦阻力的多次突跳是由微观结构下不全位错向全位错的发展所致；最后定量化分析位错、孪晶等不同变形机制对总应变的贡献比重，得到摩擦过程中位错滑移原子的应变贡献比重稳定在10%左右，而孪晶迁移的应变贡献比重稳定在2.5%左右。
关键词：纳米Cu薄膜；三维；桥域法；纳米摩擦；位错
文章编号：1004-0609(2018)-11-2305-08 中图分类号：O346 文献标志码：A
材料微观结构的本质差异性使得其在外部作用下的变形反应千差万别，研究材料微纳观尺度下的结构变化特征对认识与改造材料的宏观表现意义重大。一方面，随着人类对物质构成认识的不断加深，关于材料弹性、塑性、强度等力学特性的宏观理论体系得到了不断完善，但微观下的认识还有待进一步丰富；另一方面，随着超精密仪器在工业生产上的推广，人们对材料加工精度的要求日益提高，材料的微纳米加工技术在表面科学、电子学等领域内得到越来越多的重视。材料间接触与摩擦问题一直受到研究者们的重视，研究材料微纳尺度下的摩擦学行为对超精密仪器的设计加工、工程材料的抗磨损改进设计等方面具有相当大的指导意义[1-2]。
考虑到实验方法对各类测试条件的选取灵活性较低，相比之下，计算机数值模拟方法具有操作成本更低、环境可控性更高等独特优势，是与实验观测相辅相成的主要科研手段之一，因此被广泛应用于目前的研究当中。同时，为尽可能避免边界效应，提高计算效率和模拟结果的可靠性，有限元和分子动力学耦合的多尺度模拟方法逐渐引起人们的关注，本文所采用的桥域多尺度方法即是一种较为成熟的多尺度数值模拟方法。
目前，微纳摩擦行为的数值模拟研究大多基于分子动力学方法，刘小明等[3-4]研究了Ni晶体薄膜摩擦过程的弹塑性变形纳观机制及位错与薄膜晶界的作用关系，采用位错机制来解释塑性变形下原子尺度黏-滑现象的机理；CHAMANI等[5]模拟了柱状纳米Ni晶体的摩擦行为，分析了晶粒尺寸、形貌等对摩擦因数的影响；CHEN等[6]研究了Ni晶体薄膜摩擦过程中摩擦速度对热耗散机制的影响。但到目前为止，对摩擦过程中V形位错微结构演化的详细讨论以及位错原子数目和不同变形机制对总应变贡献比重的定量化研究还鲜见报道。
另一方面，Cu材料因其良好的导电性、传热性及抗腐蚀性而广泛应用于各种功能型工程材料中，更低的电阻率和更高的抗电迁移能力使得Cu薄膜在电子材料领域显现出日益广泛的应用前景[7]。因此，本文作者采用桥域多尺度方法对Cu薄膜表面的摩擦过程进行三维模拟，通过这一较为前沿的多尺度数值计算方法，从微观演化及量化统计等较为新颖的角度展开分析讨论。在此，主要对不同摩擦阶段Cu薄膜内的多层滑移、V形位错结构演化等展开详细分析，并通过对不全位错、全位错原子数目及位错、孪晶等变形机制的应变贡献比重的定量化统计，深入揭示微观结构变化与宏观力学行为的密切联系，对认知球形压头在三维Cu薄膜上表面摩擦过程的规律和参数有理论意义。
1 多尺度模拟方法与模型
1.1 方法
目前，应用较为成熟的多尺度方法主要有：准连续介质法(Quasicontinuum method, QC) [8]和桥域法(Bridging domain method, BD) [9]，相较于QC方法仅适用于二维模型，本文采用BD方法可实现三维模型的多尺度数值模拟，更有利于刻画真实的材料变形过程。桥域法是将研究区域分为细尺度区域与粗尺度区域[10]。细尺度区域处理与分子动力学方法一样，进行精确的原子描述，而在粗尺度区域采用有限元网格描述，粗、细尺度耦合部分通过桥域关系进行连接，完成信息的传递。桥域法通过对原子区域和连续介质区域的分别处理及合理耦合，能够较好地兼顾分子动力学方法与有限元方法的优势，达到计算效率和模型尺寸上的优化。原子区域上，引入EAM(Embedded atom method)对势[11-12]，即嵌入原子法，其基本思想是将晶体分为：1) 晶格点阵上原子之间相互作用对势；2) 原子镶嵌在电子云背景中的嵌入能，代表多体相互作用。连续介质区域上，采用CB(Cauchy-Born)法则[13]，即不需要追踪每个系统内原子，通过对代表原子的考察描述局部区域变形。
1.2 模型
文中数值模拟基于面心立方结构(FCC)Cu材料进行。对Cu原子，其单位晶胞边长r=3.615×10-10 m。桥域法几何模型如图1所示，原子区域由Lammps建立模型，连续介质区域由Gmsh根据设定的几何形状与网格尺寸建立有限元网格，最后通过Libmultiscale完成对原子区域与连续介质区域的桥接。 X、Y、Z方向尺寸均取50r(约18 nm)，其中包括原子区域(50r×50r×16r)、连续介质区域(50r×50r×38r)及桥接区域(50r×50r×4r)。连续介质区采用逐步粗化的网格划分，在保证计算精度的同时减少计算时间。由于界面波反射效应的存在，桥接区尺寸是影响计算精度的重要因素，本文参考ANCIAUX等[14]将桥接区厚度设置为4r。模拟过程设定在X、Z及Y方向上，表面均为自由边界，下表面固定。
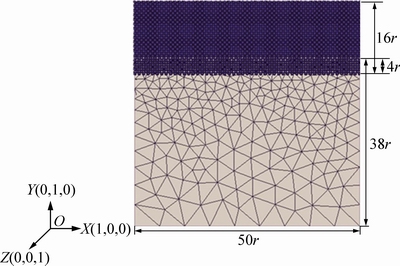
图1 Cu薄膜桥域模型示意图
Fig. 1 Schematic diagram of Cu film bridging domain model
摩擦过程中，采用刚性球形压头从Cu薄膜上表面左端正中位置以0.0002r/fs(约72 m/s)的速度沿X轴[1,0,0]方向平移。图2所示为压头摩擦Cu薄膜位置示意图。由图2可知，其中压头半径为8r(约2.8 nm)，压入深度为2.5r(约0.90 nm)。在模拟过程中，时间步设定为1×10-15 s，即1 fs，每一时间步计算得到各原子(节点)的位置、位移、受力及系统的势能。
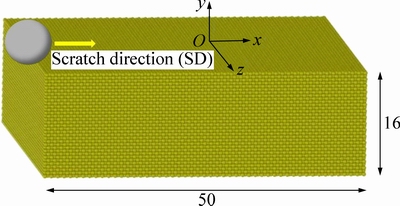
图2 压头摩擦Cu薄膜位置示意图
Fig. 2 Schematic of indenter position during scratch process (Unit: mm)
2 模拟结果与分析
2.1 摩擦阻力-摩擦距离曲线
图3所示为摩擦过程中摩擦阻力变化曲线。摩擦阻力通过计算压头在X方向上的所受原子作用力总和得到。初始阶段摩擦阻力随摩擦距离的增加不断上升，总体呈线性增长，至A点(1.5 nm)处首次出现明显下降，之后仍呈线性上升至B点(2.1 nm)处；B点后摩擦阻力上升趋于平缓，总体呈往复振荡变化，这是滑动过程中由表面原子势垒的周期性引起的黏-滑效应[3, 15]。C点(3.2 nm)、D点(3.8 nm)、E点(4.8 nm)、F点(6.8 nm)为摩擦过程中几个较显著的峰值点(将结合微观结构演化在下文进一步分析)。
图3所示为摩擦阻力-摩擦距离曲线。由图3中摩擦阻力曲线结合宏观力学初步判断，B点为摩擦过程的静-动转化点，摩擦至B点(2.1 nm)前，薄膜变形处于弹性阶段，B点之后变形进入塑性阶段。
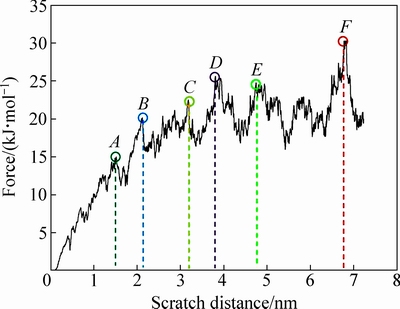
图3 摩擦阻力-摩擦距离曲线
Fig. 3 Evolution of friction force on scratch distance
2.2 系统变形能-摩擦距离曲线
在摩擦过程中，与压头接触的铜原子不断受到挤压，Cu薄膜内原子排布显著变化，系统变形能随摩擦距离变化总体呈上升趋势，结果如图4所示。结合图3和4，可见在摩擦过程中系统能量变化与摩擦阻力变化趋势相近，总体均表现为先上升后频繁振荡。在图4能量曲线上标注出图3中A~F各点位置，可见变形能曲线与摩擦阻力曲线的峰值点位置基本重合，结合功能转换关系，克服摩擦阻力做功与系统变形能间的直接联系决定了图3与图4中曲线变化的一致性。
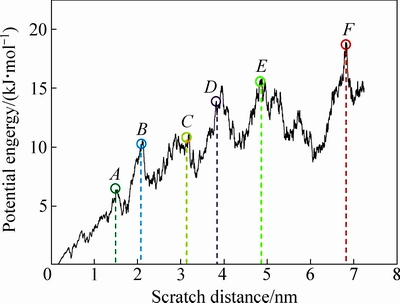
图4 系统变形能-摩擦距离曲线
Fig. 4 Evolution of deformation energy on scratch distance
2.3 摩擦微观变形分析
为解释铜薄膜的微观变形机理，对图3中摩擦阻力曲线上峰值点(A~E)的原子组态变化作进一步分析讨论。文中原子组态图像均采用可视化软件Ovito[16]作后处理得到，其中原子根据位移大小进行标色。
如图5所示，压头摩擦至1.5 nm(A点)时， Cu薄膜左侧面出现两条浅色滑移带(见图5(a))，这是压头下方原子受到挤压发生位移造成的，滑过1.5 nm后可见滑移带消失(见图5(b))，材料并未形成永久缺陷，此时薄膜变形处于弹性阶段。读取局部浅色区域原子位移可知，其滑移方向沿[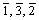
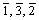]和[]，并非FCC晶体易滑移晶向，此时的原子滑移主要是初始阶段压头逐步压入薄膜表面造成的。
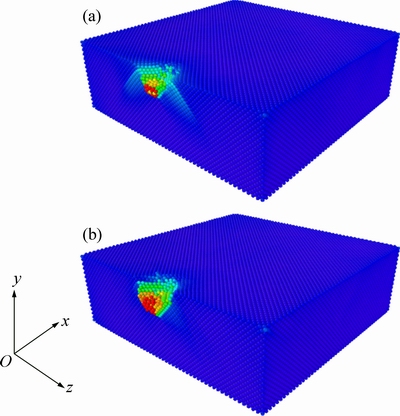
图5 摩擦1.5 nm前后原子组态
Fig. 5 Atomic configurations before (a) and after (b) scratching to 1.5 nm
图6 摩擦2.1 nm前后原子组态
Fig. 6 Atomic configurations before and after scratching to 2.1 nm
压头摩擦至2.1 nm(B点)前后原子排布情况如图6所示，对整体图沿xy平面剖视后对压头下方薄膜原子进行局部放大，可见压头摩擦至2.1 nm后，Cu薄膜亚表面原子发生明显贯穿行为，同时压头前端开始出现明显原子堆积，此时薄膜进入塑性变形阶段，完成静-动摩擦转化。
压头摩擦至3.2 nm(C点)和3.8 nm(D点)时Cu薄膜原子位移情况如图7所示，对比图6可知，摩擦至3.2 nm后摩擦阻力突降是由Cu薄膜亚表面形成4层原子的整体滑移所致(见图6中红色平行线)，这与梅继法等[17]的研究结果相一致。文献[17]对广义孪晶能的讨论分析表明，微观结构变化中将直接形成4层或以上的稳定多层滑移，而不会出现1~3层原子的滑移结构，这是由于1~3层原子孪晶能曲线无明显能量低谷，难以在变形中稳定存在，从4层原子厚度的孪晶能曲线开始出现稳定的能量低谷，故4层及以上的原子整体滑移是相对稳定的。直至压头摩擦至3.8 nm处，上述4层滑移原子并未继续发展，而压头运动的左前方出现大量原子位移堆积，导致图3中D点处摩擦阻力显著增大。
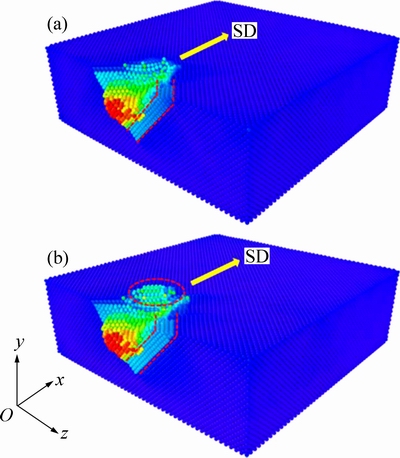
图7 摩擦至3.2 nm和3.8 nm时原子组态
Fig. 7 Atomic configurations of scratching to 3.2 nm (a) and 3.8 nm (b)
图8所示为摩擦至4.8 mm时原子组态。由图8可知，当摩擦至4.8 nm(E点)时，相较于图7(b)中Cu薄膜亚表面在原有4层滑移带外部再次发展出新的5层原子滑移带(见图8中红色平行线)，这与文献[17]中关于4层与5层原子均可形成稳定滑移的结论是相一致的。同时Cu薄膜上表面已出现一条明显的浅色滑移带，且沿斜向而非压头摩擦方向发展。进一步以[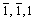
]与[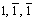
]平面截取得到黑色方框区域的局部放大(见图8(b))，读取数据可知V形滑移带原子厚度与压头压入深度接近，滑移方向沿[1，0，1]。由位错理论[18]可知，滑移方向[1，0，1]为FCC晶体易滑移系，对晶体内部变形释放起主导作用(此处V形结构将在下文作进一步讨论)。
图8 摩擦至4.8 nm时原子组态
Fig. 8 Atomic configurations of scratching to 4.8 nm
3 讨论
3.1 摩擦过程中期V形位错的产生与发射
为进一步讨论图8中所示V形结构的产生与演化过程，以中心对称系数P[19]刻画图3中C~E阶段的原子位错滑移情况，结果如图9所示。中心对称系数通过计算单个原子周围环境的混乱程度，可度量原子周围的缺陷状态或是否处在表面。作图时删除所有P≤0.5的Cu原子，在确定层错面时(4＜P≤10)标黄色；对位错原子(0.5＜P≤4)标红色；对P＞10原子标深蓝色。由于边界表面上原子中心对称系数较大，均为深蓝色。
由图9可看出，摩擦至3.2 nm附近时压头下方和侧后方已出现斜向层错面，位错原子包裹在层错面边缘。随着摩擦的进行，在薄膜亚表面沿[1，0，1]方向发射出一个V形位错，包含法向分别为[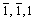]与[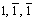]的两个层错面，且该V形结构逐渐脱离压头与薄膜接触区域，在薄膜亚表面保持稳定地向边缘斜向发射，可确定此阶段内Cu薄膜的摩擦塑性变形通过V形位错结构的运动向远处释放。
3.2 摩擦过程中不同位错原子数目的统计分析
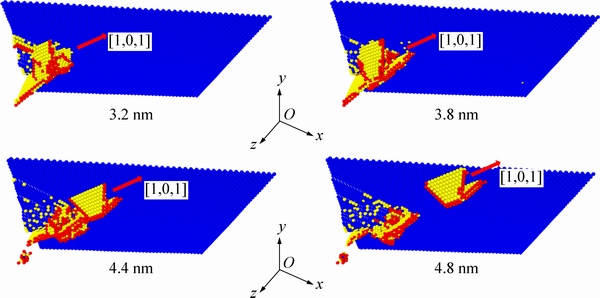
图9 摩擦过程中C~E阶段V形位错发展
Fig. 9 Generation and emission of V shape dislocation during scratch stage C-E characterized by centrosymmetry parameter
上文中针对摩擦阻力曲线峰值点所对应的微观原子组态进行分析，以下将通过定量化统计分析得到摩擦过程中位错原子数目的变化曲线。对不全位错原子和全位错原子进行量化统计，可通过计算原子滑移矢量[20](Slip vector)sα，并与Cu晶体中不全位错、全位错的 Burgers 矢量理论值相比较来完成。原子滑移矢量sα代表原子α对其近邻原子的相对位移。根据原子的滑移矢量大小可对原子分类：当一个原子处在由不全位错滑移引发的层错中时，其滑移矢量的大小接近0.148 nm(Cu晶体中不全位错 Burgers 矢量理论值)；而当原子被一个全位错穿过时，其滑移矢量的大小接近0.256 nm(Cu晶体中全位错 Burgers 矢量理论值)。据此通过对原子滑移矢量sα大小的判断，实现对系统中参与不全位错和全位错滑移原子数目的统计。图10所示为摩擦过程中不全位错和全位错原子数目随摩擦距离的变化曲线。
由图10(a)可见，不全位错原子数目随摩擦过程进行呈总体上升趋势，且过程中伴随多次明显的突跳现象。在图10(a)中以A1~F1标出曲线的主要突跳点位置，同时标出图3中A~F各突跳点位置，值得注意的是，二者具有很好的对应关系，且每次不全位错原子数目激增均发生在相应阶段摩擦阻力的突跳之前，表明摩擦过程中有多次不全位错的集中发生，正是微观下不全位错向全位错的发展导致了宏观下摩擦阻力的突跳现象，揭示了微观结构变化决定宏观力学行为的本质。
由图10(b)可知，全位错原子数目随摩擦过程进行持续增加，明显不同于图10(a)中不全位错原子数目的不断突跳变化，全位错原子数目增加过程中仅出现小幅波动，在个别阶段有阶跃性增加，可以认为整个摩擦过程中全位错表现为一个累积的上升过程。
3.3 摩擦过程中位错、孪晶等不同变形机制的应变贡献分析
通过定量化统计，进一步分析位错、孪晶等不同变形机制对总应变的贡献比重。为了对位错、孪晶等变形机制的应变贡献程度进行比较，需要获得材料内部的应变分布，本文采用原子Green应变张量E作为度量。为了估计应变程度的大小根据式(1)计算Mises等效应变：
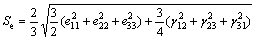(1)
式中：eii是偏应变：
(2)
而γij是工程剪应变：
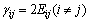(3)
通过将对应于特定变形机制内原子的等效应变相加可以获得其变形程度，将所有原子的等效应变相加可以得到系统的总体等效应变，二者相除从而获得特定变形机制对总体等效应变的贡献比重。同时作为对照，将Cu薄膜内部所有仍保持FCC 结构的原子等效应变相加，用来量化没有参与上述变形机制(位错滑移和孪晶迁移等)部分的变形程度。
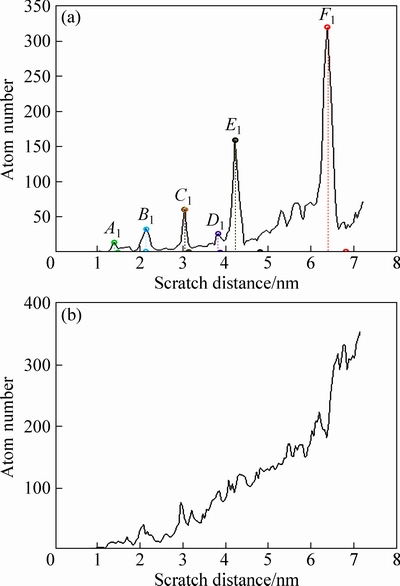
图10 位错原子数目变化曲线
Fig. 10 Evolution of number of partial dislocation atoms (a) and perfect dislocation atoms on scratch distance (b)
如3.2节所述，通过原子滑移矢量大小sα的判定可计算得到位错滑移相关的应变贡献，而对孪晶迁移相关的变形，采用Tucker[21]的定量化后处理方法来判定原子是否参与孪晶迁移。该方法依赖于计算原子的微转动张量[22](Atomic microrotation tensor)Rskew，首先根据原子及其最近邻原子的坐标可以获得其变形梯度张量[23]，其计算方法如下：
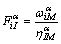(4)
其中，
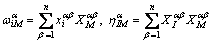(5)
式中：xαβ是在当前构型下从原子α到其近邻原子β的矢量；而Xαβ是在无变形的初始构型下的上述矢量。把张量F分解为旋转部分R和拉伸部分U，F=RU，从而微旋转张量Rskew可作如下计算：
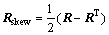(6)
进一步可定义微旋转矢量φ为
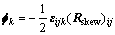(7)
式中：ε为置换张量 (permutation tensor)。微旋转矢量的大小代表了局部非均匀旋转形变的程度，这一变形机理是孪晶化原子的特性之一，因此可将微旋转矢量的大小作为孪晶迁移的一个判据。
图11所示为摩擦过程中位错、孪晶等变形机制原子对总应变贡献比重随摩擦距离的变化曲线。如图11可见，位错滑移(包括不全位错、全位错)对总体应变的贡献比重变化表现为先上升随后趋于稳定，所占比重并不大，最终稳定在10%左右。这是由于Cu薄膜表面摩擦过程属于材料的局部变形行为而非全局变形，位错滑移多发生于薄膜亚表面局部区域。孪晶迁移对总体应变的贡献比重变化亦表现为上升后趋于稳定，但相较于位错滑移更小，应变贡献比重稳定在2.5%，为位错应变贡献的1/4左右。此外，未参与位错、孪晶等剧烈变形机制的FCC原子对系统总应变的贡献比重较大，这是因为铜材料本身为FCC原子结构，但随摩擦过程的进行，摩擦接触使得局部FCC结构被不断破坏，贡献比重呈下降趋势，最终稳定在40%左右。图11中 GB(Grain boundary)曲线包含摩擦中薄膜表面形成的缺陷、原子重排、自由体积迁移等，参与多种复杂变形的GB原子对总应变贡献不断增加，这是由于摩擦这一局部施载行为对薄膜表面形貌破坏严重，局部应变程度剧烈。
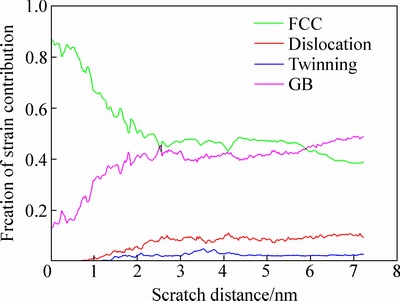
图11 位错、孪晶等变形机制的应变贡献比重变化曲线
Fig. 11 Evolution of strain contribution of dislocation and twinning on scratch distance
4 结论
1) 摩擦过程中摩擦阻力与系统变形能变化趋势基本一致，二者主要峰值点位置高度重合，符合功能转换关系。
2) 摩擦过程中存在静-动转化点。静摩擦阶段薄膜以弹性变形为主，局部出现可恢复变形，转化为动摩擦后薄膜以塑性变形为主。动摩擦阶段Cu薄膜亚表面发生两次层数稳定的原子整体滑移(分别为4层和5层)，这一现象与相关广义孪晶能的研究结果相 一致。
3) 通过中心对称系数刻画薄膜亚表面滑移带内部V形位错的产生和演化过程，表明薄膜亚表面的塑性变形通过V形位错的运动向远处释放。
4) 摩擦阻力的多次突跳与Cu薄膜内的不全位错滑移关系密切，摩擦过程中不全位错的集中发生均出现在摩擦阻力突跳之前，说明微观不全位错向全位错的发展是导致宏观摩擦阻力突跳的根本原因。
5) 摩擦行为是一个局部表面变形过程，位错滑移在此过程中对总应变的贡献比重最终稳定在10%左右，而孪晶迁移对总应变的贡献比重稳定在2.5%左右。
REFERENCES
[1] 刘 更, 刘天祥, 温诗铸. 微/纳尺度接触问题计算方法研究进展[J]. 力学进展, 2008, 38(5): 521-544.
LIU Geng, LIU Tian-xiang, WEN Shi-zhu. Advances in computational methods of micro/nano scale contact problems[J]. Advances in Mechanics, 2008, 38(5): 521-544.
[2] 雒建斌, 何 雨, 温诗铸, 钟 掘. 微/纳米制造技术的摩擦学挑战[J]. 摩擦学学报, 2005, 25(3): 283-288.
LUO Jian-bing, HE Yu, WEN Shi-zhu, ZHONG Jue. Challenges to tribology arisen from the development of micro- and nano-manufacturing technology[J]. Tribology, 2005, 25(3): 283-288.
[3] 刘小明, 由小川, 柳占立, 庄 茁. 纳米尺度摩擦过程的分子动力学模拟[J]. 金属学报, 2008, 44(9): 1025-1030.
LIU Xiao-ming, YOU Xiao-chuan, LIU Zhan-li, ZHUANG Zhuo. Molecular dynamics simulation of nanoscale friction process[J]. Acta Metallurgica Sinica, 2008, 44(9): 1025-1030.
[4] 刘小明, 由小川, 柳占立, 聂君锋, 庄 茁. 纳米Ni薄膜在摩擦过程中塑性行为的分子动力学模拟[J]. 金属学报, 2009, 45(2): 137-142.
LIU Xiao-ming, YOU Xiao-chuan, LIU Zhan-li, NIE Jun-feng, ZHUANG Zhuo. Molecular dynamics simulation of plastic behavior of the Ni nanofilm during scratch process[J]. Acta Metallurgica Sinica, 2009, 45(2): 137-142.
[5] CHAMANI M, FARRAHI G H, MOVAHHEDY M R. Friction behavior of nanocrystalline nickel near the Hall-Petch breakdown[J]. Tribology International, 2017, 107: 18-24.
[6] CHEN K, WANG L, CHEN Y, WANG Q. Molecular dynamics simulation of microstructure evolution and heat dissipation of nanoscale friction[J]. International Journal of Heat & Mass Transfer, 2017, 109: 293-301.
[7] 张 莉, 严学俭, 朱国栋, 曾志刚, 沈 淼, POHLERS A. 铜薄膜在100 ℃~400 ℃下氧化行为的微观表征[J]. 真空科学与技术学报, 2006, 26(4): 268-271.
ZHANG Li, YAN Xue-jian, ZHU Guo-dong, SHEN Miao, POHLERS A. Variations in Microstructures of Copper Film Oxidation at 100 ℃-400 ℃[J]. Chinese Journal of Vacuum Science and Technology, 2006, 26(4): 268-271.
[8] TADMOR E B. The quasicontinuum method[M]. Brown University, 1996.
[9] XIAO S P, BELYTSCHKO T. A bridging domain method for coupling continuum with molecular dynamics[J]. Computer Methods in Applied Mechanics & Engineering, 2004, 193(17/20): 1645-1669.
[10] 张 征, 刘 更, 刘天祥, 崔俊芝. 计算材料科学中桥域多尺度方法的若干进展[J]. 计算力学学报, 2006, 23(6): 652-658.
ZHANG Zheng, LIU Geng, LIU Tian-xiang, CUI Jun-zhi. Advances in computational materials science with multiscale method of Bridge domain[J]. Chinese Journal of Computational Mechanics, 2006, 23(6): 652-658.
[11] NORSKOV J K, LANG N D. Effective-medium theory of chemical binding: application to chemisorptions[J]. Physical Review B,1980,21(6): 2131-2136.
[12] DAW M S, BASKES M I. Embedded-atom method: derivation and application to impurities, surface, and other defects in metals[J]. Physical Review B, 1984, 29(12): 6443-6453.
[13] ERICKSEN J L. The Cauchy and Born hypotheses for crystals[J]. Phase Transformations and Material Instabilities in Solids, 1983: 61-77.
[14] ANCIAUX G, MOLINARI J F. Contact mechanics at the nanoscale—A 3D multiscale approach[J]. International Journal for Numerical Methods in Engineering, 2009, 79(9): 1041-1067.
[15] TOMLINSON G A. CVI. A molecular theory of friction[J]. Philosophical Magazine, 1962, 46: 905-939.
[16] STUKOWSKI A. Visualization and analysis of atomistic simulation data with OVITO—The open visualization tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(6): 2154-2162.
[17] 梅继法, 黎军顽, 倪玉山, 王华滔. 体心立方Ta的广义面错能及在Ⅱ型裂纹尖端初始塑性研究中的应用[J]. 物理学报, 2011, 60(6): 506-513.
MEI Ji-fa, LI Jun-wan, NI Yu-shan, WANG Hua-tao. Generalized planar fault energy of body-centered cubic Ta and its application to plastic deformation of mode Ⅱ crack tip[J]. Acta Physica Sinica, 2011, 60(6): 506-513.
[18] HIRTH J P, LOTHE J L. The theory of dislocations[M]. New York: John Wiley and Sons, 1982: 772-789.
[19] KELCHNER C L, PLIMPTON S J, HAMILTON J C. Dislocation nucleation and defect structure during surface indentation[J]. Physical Review B, 1998, 58(17): 11085-11088.
[20] ZIMMERMAN J A, KELCHNER C L, KLEIN P A, HAMILTON J C, FOILES S M. Surface step effects on nanoindentation[J]. Physical Review Letters, 2001, 87(16): 165507-165516.
[21] TUCKER G J, FOILES S M. Quantifying the influence of twin boundaries on the deformation of nanocrystalline copper using atomistic simulations[J]. International Journal of Plasticity, 2015, 65: 191-205.
[22] TUCKER G J, ZIMMERMAN J A, MCDOWELL D L. Continuum metrics for deformation and microrotation from atomistic simulations: Application to grain boundaries[J]. International Journal of Engineering Science, 2011, 49(12): 1424-1434.
[23] ZIMMERMAN J A, BAMMANN D J, GAO H. Deformation gradients for continuum mechanical analysis of atomistic simulations[J]. International Journal of Solids and Structures, 2009, 46(2): 238-253.
Multiscale simulation analysis of nano-Cu scratch process with bridging domain method
GUI Jun-min, NI Yu-shan
(Department of Aeronautics and Astronautics, Fudan University, Shanghai 200433, China)
Abstract: The scratch process of nano-Cu film has been investigated by using Bridging domain method. The friction force and system deformation energy vary with scratch distance in a similar trend, and there is a static-dynamic transition point in the scratch process. The microstructural analysis shows that the restorable strain occurs locally in Cu film at elastic stage, and then with the pile-up atoms in the front of indenter, the deformation of Cu film turns into plastic stage. The stable multilayer slip and a slanting slip zone along [1,0,1] are captured under the indenter.The generation and evolution of V shape dislocation in the slanting slip zone are analyzed via the centrosymmetry parameter, and the motion of V shape dislocation plays a leading role in the deformation release at plastic stage. In addition, statistical analysis for different dislocation atoms reveals that the development from partial dislocation to perfect dislocation leads to multiple jumps in friction force. The strain contribution analysis shows that the proportion of dislocation slip is finally about 10%, while twinning migration contributes less to the total strain, the proportion is finally about 2.5%.
Key words: nano-Cu film; three-dimension; bridging domain method; nano-friction; dislocation
Foundation item: Project(11572090) supported by the National Natural Science Foundation of China
Received date: 2017-05-08; Accepted date: 2018-09-05
Corresponding author: NI Yu-shan; Tel: +86-21-55665173; E-mail: niyushan@fudan.edu.cn
(编辑 龙怀中)
基金项目：国家自然科学基金资助项目(11572090)
收稿日期：2017-05-08；修订日期：2018-09-05
通信作者：倪玉山，教授；电话：021-55665173；E-mail：niyushan@fudan.edu.cn
