Evaluation of interface fracture toughness in

SiC fiber reinforced titanium matrix composite

YUAN Mei-ni(原梅妮), YANG Yan-qing(杨延清), HUANG Bin(黄 斌),

LI Jian-kang(李健康), CHEN Yan(陈 彦)

School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 26 October 2007; accepted 13 March 2008

Abstract: The finite element method based on the equivalent domain integral technique was developed to simulate the push out test and evaluate the interfacial fracture toughness of SiC reinforced titanium matrix composites. A special subroutine was introduced while modeling the push-out test to control interfacial failure process. In addition, the residual stresses, Poisson ratio and friction stresses were all considered in the finite element analysis and the interface debonding was described as a continuous process. The results show that the interfacial fracture toughness of SiC/Timetal-834 is about 50 J/m². Moreover, the effects of various parameters on the interfacial fracture toughness and the variations of energy release rates at both ends of the specimen were analyzed in detail.

Key words: push out test; interface fracture toughness; finite element analysis (FEA); SiC_f/Ti composite

1 Introduction

The push out test has been developed for a few years as a means of quantifying interfacial properties of SiC fiber reinforced titanium matrix composites (TMCs)[1-4]. However, the values of interfacial shear strength and frictional shear stresses obtained from the push out test are only average assessments. Since the interface stress distribution is complex due to edge effect or crack growth during the push-out test[5], the average values do not represent the real behavior of the interfaces and may lead to misleading in some cases. The finite element method, which is used to model the push out test, just predicts the real stress distribution at the interface[5-7]. Moreover, the evaluation of interfacial fracture toughness using finite element method is independent of mesh density. Unfortunately, only very few finite element simulations based on the energy failure criterion have been done. MUKHERIEE et al[8-9] and ZENG et al[10] used the finite element method based on the energy failure criterion to evaluate interfacial fracture toughness of TMCs. However, in MUKHERIEE’s analysis, the effect of frictional stress on the interfacial fracture toughness was ignored. In ZENG’s analysis, the interface debonding process was not described as a continuous one.

In this work, the finite element method based on the equivalent domain integral technique is presented to evaluate the interfacial fracture toughness of TMCs. In the finite element analysis, the effects of the residual stresses, Poisson ratio and friction stresses are all considered, and the interface debonding process is described as a continuous one.

2 Finite element analysis

2.1 Finite element model and material properties

The push out test is analyzed using an axi- symmetric cylindrical model, as shown in Fig.1. The axi-symmetric cylindrical model consists of SiC fiber and titanium alloy matrix. The height of specimen is 500 ?m, fiber radius is 70 ?m, and matrix radius is 112 ?m. The elements of SiC fiber and titanium alloy matrix are isoparametric 4-noded quadrilateral elements. The elements of interface are composed of contact-friction element and spring element. Fig.2 shows the details of the spring elements at the interface. In finite element  analysis, SiC fiber and titanium alloy matrix are treated as isotropic elastic materials. Moreover, the property dependency on temperature is considered. SiC/ Timetal-834 is taken as the model material. Table 1 lists the thermo-mechanical properties of titanium alloy matrix and SiC fiber.

Fig.1 Axi-symmetric finite element model

Fig.2 Details of spring elements

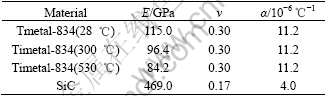
Table 1 Thermo-mechanical parameters of SiC fiber and Timetal- 834 used in finite element analysis

2.2 Numerical simulation procedure

Modeling of the push out test involves two steps.

1) Modeling the cooling process of composites. When TMCs are cooled from high temperature to room temperature, thermal residual stresses are induced due to the mismatch of the thermal expansion coefficients between fiber and titanium alloy matrix. In finite element analysis, the cooling process can be modeled by using temperature load, that is, the initial load and boundary load are added by using initial temperature and test temperature respectively. The free end surface of the model can be simulated via removing the existing tying constraint and spring elements[11-16].

2) Modeling the push out test. The push out test involves pushing a fiber out of composites through a flat indenter. In finite element analysis, the prescribing displacement is added to a rigid punch until the fiber is pushed out completely. Moreover, a special subroutine is used to control the interface debonding and frictional sliding process. The interface failure process is based on the energy failure criterion given by

G≥G_Ic                                     (1)

where  G is the energy release rate of the interface crack and G_Ic is the critical energy release rate. When the strain energy release rate of the interface crack (G) exceeds the critical value, the spring stiffness is reduced to zero and the debonding initiates.

3 Results and discussion

3.1 Evaluation of interface fracture toughness of TMCs

The finite element method based on the equivalent domain integral technique was used to simulate the push out test. When the simulated load—displacement curve has a good agreement with the experiment curve, the interfacial fracture toughness of TMCs can be obtained. In this work, SiC/Timetal-834 is selected as the model material. The load—displacement curve of the push out test for SiC/Timetal-834 is shown in Fig.3[10]. The specimen of the push-out test is the same as the finite element model. More information about the push out equipment and test procedure is given in Ref. [4].

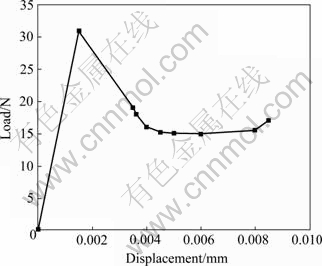
Fig.3 Load—displacement curves of push out test[10]

The finite element method based on the equivalent domain integral technique is used to simulate the push out test of SiC/Timetal-834. First, the push out test is simulated with different interfacial frictional coefficients.Fig.4(a) presents the simulated load—displacement curves with different frictional coefficients (0.3, 0.4 and 0.5). From Fig.4(a), it can be obtained that, when the interfacial frictional coefficient is assumed to be 0.4, the frictional force evaluated is equal to the experimental one. So the interfacial frictional coefficient is equal to 0.4. Then, the push out test is simulated with different critical energy release rates and a constant value of interfacial frictional coefficient (?=0.4). Fig.4(b) shows the simulated load—displacement curves with different critical energy release rates. From Fig.4(b), it can be obtained that when the critical energy release rate is assumed to be 50 J/m², good agreement is found between the simulated load—displacement curve and the experimental curve. So, the interfacial fracture toughness (the critical energy release rate) of SiC/Timetal-834 is about 50 J/m². It is noted that the effects of interface thickness and loading rate on the peak load are all neglected in the finite element analysis. Therefore, the interfacial fracture toughness evaluated by the finite element analyses has some error.

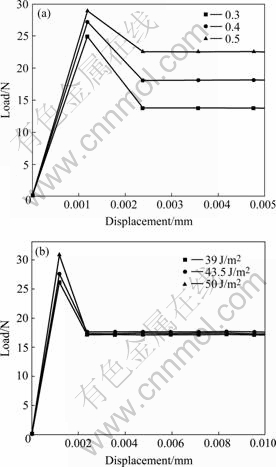
Fig.4 Simulated load—displacement curves: (a) With different frictional coefficients; (b) With different critical energy release rates

the equation of interfacial fracture toughness:

From the concept of fracture mechanics, we deduced

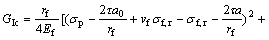
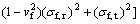              (2)

where  r_f is the radius of the fiber, E_f is elastic modulus of the fiber, σ_p is the applied stress, τ is the interfacial frictional stress, σ_{f, r} is radial thermal residual stress, σ_{f, t} is tangential thermal residual stress, ν_f  is the Poisson ratio of the fiber, a is the complete length, a₀ is the initial debonding length[10]. These parameters are summarized and listed in Table 2. Using these parameters, the interfacial fracture toughness of SiC fiber reinforced Timetal-834 is calculated to be about 46.21 J/m². This further demonstrates the interfacial fracture toughness evaluated by the finite element analysis is reasonable.

Table 2 Parameters used to examine predictions of analytical model

3.2 Effect of peak load on interfacial fracture toughness of TMCs

Fig.4(b) presents the simulated load—displacement curves with different critical energy release rates. From Fig.4(b), it can be obtained that the critical energy release rate of TMCs increases with increasing the peak load. The reason is that the strain energy in composites increases with increasing the peak load. Therefore, the interfacial fracture toughness of TMCs increases with increasing the peak load. CHANDRA and ANANTH[5] also obtained the similar conclusion that the interfacial bond strength increases with increasing the peak load.

3.3 Effect of frictional stresses on interfacial fracture toughness of TMCs

   Fig.5 presents the simulated load—displacement curves of the push out test for SiC/Timetal-834 composite. The load—displacement curves in Fig.5 have different critical energy release rates and the same peak load. In general, the critical energy release rate varies with the variation of the peak load, because the strain energy in composites varies with the peak load. However, in Fig.5, the critical energy release rates of SiC/ Timetal- 834 are different under the same peak load. that results from different interfacial frictional forces. With the increase of frictional force, the more strain energy in composites is consumed. So, the strain energy provided for creation of a new crack surface will decrease. That is to say that the interfacial fracture toughness of SiC/ Timetal-834 is decreased. LIU and KAGAWA[17], KIM and MAI[18] also demonstrated that the interfacial fracture toughness of composites is inversely proportional to the interfacial friction stress.

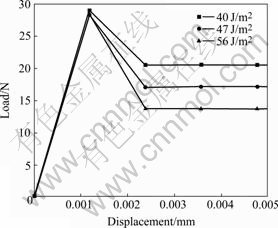
Fig.5 Simulated load—displacement curves with different critical energy release rates

3.4 Variations of energy release rate at both ends of specimen

A finite element method based on the equivalent domain integral technique is used to analyze the variations of the energy release rate at both ends of the specimen. Fig.6 shows the variations of energy release rates at both ends of the specimen for SiC/Timetal-834, evaluated by the finite element method. In Fig.6, the applied displacement u is normalized with respect to u_max, at which the interface debonding initiates. It can be seen from Fig.6 that, the energy release rate at the supported end increases from 37.6 J/m² to 45 J/m²; in contrast, the energy release rate at the loading end decreases from 37.6 J/m² to 34 J/m².

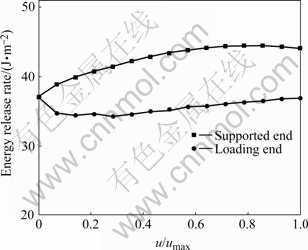
Fig.6 Variations of energy release rate at two ends of specimen

Fig.7 shows the distribution of shear residual stresses at the interface of TMCs. From Fig.7, it can be seen that the direction of shear residual stresses changes from positive at the loading end to negative at the supported end. When a compressive load is applied to the loading end, additional negative shear stresses, which are superimposed on shear residual stresses, are introduced at interface. The shear residual stresses at the loading end tend to decrease, due to the fact that the direction of shear stresses introduced by compressive load are opposite to that of shear residual stresses at the loading end. However, the shear stresses at the supported end increase, due to the fact that the direction of shear stresses introduced by compressive load are the same as that of shear residual stresses at the supported end. Therefore, the energy release rate at the supported end increases. This also explains the reason why the initial debonding of TMCs occurs at the supported end during the push out test.

Fig.7 Interfacial shear stress distribution of titanium matrix composites

4 Conclusions

1) The interfacial fracture toughness of SiC/ Timetal-834 composites evaluated is about 50 J/m².

2) The interfacial fracture toughness of TMCs increases with increasing the peak load and decreases with increasing the frictional force.

3) The distribution of shear residual stresses results in the increase of the energy release rate of SiC/Timetal- 834 composites at the supported end and the decrease at the loading end.

References

[1] FUKUSHIMA A, FUJIWARA C, KAGAWA Y. Effect of interfacial properties on tensile strength in SiC/Ti-15-3 composites [J]. Mater Sci Eng A, 2000, 276: 243-249.

[2] WEIDENMANN K A, KERSCHER E. Characterization of the interfacial properties of compound extruded lightweight profiles using the push out technique [J]. Mater Sci Eng A, 2006, 424: 205-211.

[3] K?CK T, BRENDEL A, BOLT H. Interfacial reaction between silicon carbide and interlayers in silicon carbide-copper metal matrix composites test [J]. J Nucle Mater, 2006, 362: 197-201.

[4] KALLAS M N, KOSS D A, HAHN H T, HELLMAN J R. Interfacial stress state present in a thin slice push out test [J]. J Mater Sci, 1992, 27: 3821-3826.

[5] CHANDRA N, ANANTH C R. Analysis of interfacial behavior in MMCs and IMCs by the use of thin slice push out tests [J]. Comp Sci Tech, 1995, 54: 87-100.

[6] DHERT W J A, VERHEYEN C C P M, BRAAK L H. A finite element analysis of the push out test: Influence of test conditions [J]. J Biome Mater Res, 2004, 1:119-130.

[7] QING H Q, WANG J S, KANG Y L. A theoretical model for electroelastic analysis in piezoelectric fiber push out test [J]. Arch Appl Mech, 2006, 75: 527-540.

[8] MUKHERIEE S, ANANTH C R, CHANDRA N. Evaluation of fracture toughness of MMC interfaces using thin-slice push out tests [J]. Script Mater, 1997, 36: 1333-1338.

[9] MUKHERIEE S, ANANTH C R, CHANDRA N. Effect of residual stresses on the interfacial fracture behavior of metal matrix composites [J]. Comp Sci Tec, 1997, 57: 1501-1512.

[10] ZENG W D, PETERS P W M, TANAKA Y. Interfacial bond strength and fracture energy at room and elevated temperature in titanium matrix composites (SCS-6/Timetal 834) [J]. Composites, 2002, 33A: 1159-1170.

[11] YUAN M N, Yang Y Q. Analysis of interfacial behavior in titanium matrix composites by using the finite element method (SCS-6/Ti55) [J]. Scripta Mater, 2007, 56: 533-536.

[12] CHANDRA N, LI H, SHET C, GHONEM H. Some issues in the application of cohesive zone models for metal-ceramic interfaces [J]. Int J Solids Struct, 2002, 39: 2827-2855.

[13] KALTON A F, HOWARD S J, JANCZAK J, CLYNE T W. Measurement of interfacial fracture energy by single fiber push out testing and its application to the titanium silicon carbide system [J]. Acta Mater, 1998, 46: 3175-3189.

[14] XU ROY L, HUACHENG K, SPREEPARNA S. Free edge stress singularities and edge modifications for fiber push out experiments [J]. J Comp Mater, 2005, 39: 1103-1125.

[15] CHEN H, HU W, ZHONG Y. Finite element analysis of single fiber push out tests of continuous Al₂O₃ fiber-reinforced NiAl composites [J]. Mater Sci Eng A, 2007, 15: 624-632.

[16] CHANDRA N, GHONEM H. Interfacial mechanics of push-out tests: Theory and experiments [J]. Composites, 2001, 32A: 575-584.

[17] LIU Y F, KAGAWA Y. Analysis of debonding and frictional sliding in fiber reinforced brittle matrix composites: Basic problem [J]. Mater Sci Eng A, 1996, 212: 75-86.

[18] KIM JK, MAI Y W. High strength, high fracture toughness fiber composites with interface control—A review [J]. Comp Sci Tech, 1991, 41: 333-378.

(Edited by YANG Bing)