Numerical simulation of flocculation and settling behavior ofwhole-tailings particles in deep-cone thickener
来源期刊:中南大学学报(英文版)2016年第3期
论文作者:李翠平 阮竹恩 石聪
文章页码:740 - 749
Key words:whole-tailings particles; flocculation settling; numerical simulation; deep-cone thickener; population balance model
Abstract: Rapid dewatering and thickening of whole-tailings with ultrafine particles is one of the most important processes for the whole-tailings paste preparation. Deep-cone thickener, a kind of such process for the flocculation and settling of whole-tailings, is particularly necessary to study. However, there exist many problems in observing the flocculation and settling process of whole-tailings, as well as the particle size distribution (PSD) of whole-tailings floccules in deep-cone thickener. Population balance model (PBM) is applied to predict the PSD in deep-cone thickener, and LUO model and GHADIRI model are employed to study the aggregation and fragmentation mechanism of the whole-tailings particles, respectively. Through three-dimensional numerical simulation on the whole-tailings flocculation and settling in deep-cone thickener using computational fluid dynamics (CFD)-PBM, the distribution of density and turbulent kinetic energy in deep-cone thickener were obtained, at the same time the spatio-temporal changes of whole-tailings floccules particle size distribution are analyzed. Finally, the major flocculation position in deep-cone thickener is found and the flocculation settling rules of whole-tailings are achieved.
J. Cent. South Univ. (2016) 23: 740-749
DOI: 10.1007/s11771-016-3119-8

RUAN Zhu-en(阮竹恩)1, 2, LI Cui-ping(李翠平)1, 2 , SHI Cong(石聪)1, 2
1. School of Civil & Environmental Engineering, University of Science & Technology Beijing, Beijing 100083, China;
2. Key Laboratory of Ministry of Education of China for Efficient Mining and Safety of Metal Mines
(University of Science & Technology Beijing), Beijing 100083, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: Rapid dewatering and thickening of whole-tailings with ultrafine particles is one of the most important processes for the whole-tailings paste preparation. Deep-cone thickener, a kind of such process for the flocculation and settling of whole-tailings, is particularly necessary to study. However, there exist many problems in observing the flocculation and settling process of whole-tailings, as well as the particle size distribution (PSD) of whole-tailings floccules in deep-cone thickener. Population balance model (PBM) is applied to predict the PSD in deep-cone thickener, and LUO model and GHADIRI model are employed to study the aggregation and fragmentation mechanism of the whole-tailings particles, respectively. Through three-dimensional numerical simulation on the whole-tailings flocculation and settling in deep-cone thickener using computational fluid dynamics (CFD)-PBM, the distribution of density and turbulent kinetic energy in deep-cone thickener were obtained, at the same time the spatio-temporal changes of whole-tailings floccules particle size distribution are analyzed. Finally, the major flocculation position in deep-cone thickener is found and the flocculation settling rules of whole-tailings are achieved.
Key words: whole-tailings particles; flocculation settling; numerical simulation; deep-cone thickener; population balance model
1 Introduction
With the development of backfilling technology, tailings are used as the main backfilling materials for filling the goaf area. Researches have focused on the whole-tailings paste backfilling technology [1-2]. The whole-tailings with ultrafine particles have a low sedimentation velocity and poor permeability, and their dewatering and thickening are very difficult. Therefore, it is important to find a rapid way to dewater and thicken whole-tailings with ultrafine particles for the whole-tailings paste preparation [2]. Study on the flocculation and settling of whole-tailings in deep-cone thickener is particularly urgent.
Both experimental studies and numerical simulations on the behavior and mechanism of particle settling were conducted by many researchers and also a series of results were achieved.
B URGERA et al [3] presented a mathematical model on the continuous sedimentation and concentration to simulate their experimental results. They provided a numerical algorithm for the continuous sedimentation and technical supports for the thickener design. USHER et al [4-5] established a macro distribution parameter equation for the settling process. They analyzed the impact of solid concentration and deposition fluxes on settling velocity using settling curve, and obtained the industrial indicators, such as underflow concentration and thickener area. SPEHAR et al [6] gave a macro-mechanics description on the influence of gel concentration, compressive yield stress, shear yield stress, as well as sedimentation coefficient on the structure strength of floccules. ESWARAIAH et al [7] analyzed the settling characteristics of ultrafine iron ore slimes under various pH values, as well as different kinds of flocculants in different dosages. DU et al [8] macroscopically studied the impact of flocculation and rake action on floccule structure, and qualitatively described the changes of floccule structure. They put forward the existence of floccule inner water and drainage channel under stirring. SELOMUYA et al [9] developed a 3-D visualization on the microstructures of floccule particles and sedimentary layer using X-ray micro tomography and lattice Boltzmann method.
URGERA et al [3] presented a mathematical model on the continuous sedimentation and concentration to simulate their experimental results. They provided a numerical algorithm for the continuous sedimentation and technical supports for the thickener design. USHER et al [4-5] established a macro distribution parameter equation for the settling process. They analyzed the impact of solid concentration and deposition fluxes on settling velocity using settling curve, and obtained the industrial indicators, such as underflow concentration and thickener area. SPEHAR et al [6] gave a macro-mechanics description on the influence of gel concentration, compressive yield stress, shear yield stress, as well as sedimentation coefficient on the structure strength of floccules. ESWARAIAH et al [7] analyzed the settling characteristics of ultrafine iron ore slimes under various pH values, as well as different kinds of flocculants in different dosages. DU et al [8] macroscopically studied the impact of flocculation and rake action on floccule structure, and qualitatively described the changes of floccule structure. They put forward the existence of floccule inner water and drainage channel under stirring. SELOMUYA et al [9] developed a 3-D visualization on the microstructures of floccule particles and sedimentary layer using X-ray micro tomography and lattice Boltzmann method.
Numerical simulation has been widely used to study sedimentation process in stirred tank reactor and thickener in recent years. Computational fluid dynamics (CFD) is a commonly used method of numerical simulation, which is specialized in predicting the distribution of solid particle concentration, the form of multiphase flow field, the fluid shear rates and the aggregation size of red mud particles under flocculating [10-12]. CFD can numerically simulate the changes in the flow trajectory and flocculation effects of tailings due to the variation in the structures of feedwell [13-16]. OWEN et al [14] studied the effects of central cylinder and flocculate on the adsorption and sedimentation process of red mud particles in gravity thickeners feedwells. Similarly, KAHANE et al [12, 17] studied the effects of the structure of central cylinder and location of flocculant addition on the performance of the settling tank, and got an optimization result.
In recent years, CFD coupled with population balance model (PBM) has been used to study central cylinder. CFD-PBM is one of the most advanced and powerful tools to study the central cylinder, because it can not only predict the flow field (the ability of CFD), but also calculate the particle size distribution (PSD) of gases, liquids and solids (the advantages of PBM) [18-20]. NGUYEN et al [18] and HEATH and PETER [20] solved two sets of continuity equations and momentum equations for liquid and solid phase, respectively. The two sets of equations were coupled with a common pressure field with an interphase momentum exchange to calculate the shear rate of turbulent. HEATH and PRTER [20] studied the influence of flocculants type and injection position on the red mud aggregation size. NGUYEN et al [18] introduced PBM model and other physical equations using formula translation. They applied 35 sets of particles as the secondary phase. The 35 sets of scalar equations share a common velocity field, but have their own concentration gradient and the source phase. The effect of feed flow rate on the distribution of solid, the shear rate, the adsorption efficiency of the flocculant, the particle size of aggregates, the particle aggregation process, and the flow characteristics in the central cylinder were studied. They concluded that increasing the feed flow rate in a certain range will result in a few benefits: 1) promoting mixing and flow diluting in central cylinder, 2) increasing the shear rate, 3) making the distribution of the fluid uniform, and 4) increasing the residence time, the efficiency of flocculant adsorption and polymerization and the maximum size of the polymeric particles.
CFD-PBM method has been widely used to study the particle sedimentation in stirred tank by many researchers. Simulation on the sedimentation process in stirred tank was first proposed by WEI and GARSIDE [21-22], and further studied by the other researchers [23-27]. JAWORSKI and NIENOW [24] and WANG et al [25] simulated the continuous sedimentation process of BaSO4 in stirred reactor using quadrature method of moments (QMOM). However, the aggregation and breakage were ignored during their simulation. WANG et al [25] analyzed the effects of the feed position, the feed concentration, the stirring speed, the residence time and the draft tube on the sedimentation process of BaSO4 in continuous stirred reactor. They ignored the aggregation and breakage, therefore the deviation between the simulation and experimental results grew with the feed concentration increasing consequently. VICUM and MAZZOTTI [26] adopted standard method of moments (SMM) under the condition of neglecting the aggregation and breakage process to study the effect of turbulent mixing on BaSO4 sedimentation in a semi-continuous stirred tank, and it was found that simulation result was in good agreement with the experimental value at small feed concentration, whereas the simulation result was larger than the experimental value at higher feed concentration. Taking nucleation, crystal growth, aggregation and breakage into account, CHENG et al [23, 27] simulated the continuous sedimentation process of BaSO4 using the QMOM coupled with CFD. The numerical results and published experimental data have a good consistency. At the same time, the effects of different factors were well studied.
Throughout the existing research results, many studies have been conducted in particle settling, compression settlement of flocculation, and settlement mechanism of tailings. Although great progresses have been made, limitations still exit. The existing achievements are limited to the macroscopic settling of solid particle within only liquid fluid. Furthermore, few literatures can be found for the numerical simulation of whole-tailings flocculation and settling in deep-cone thickener, especially the spatio-temporal migration behavior of whole-tailings during the process of free settling, hindered settling and compression settling under the effect of solid-liquid two-phase coupling.
The whole-tailings flocculation and settling in a deep-cone thickener are simulated and studied using CFD-PBM coupled model in this work. The PSD and the spatio-temporal changes of whole-tailings flocculation were analyzed deeply to investigate the flocculation sedimentation rules of whole-tailings.
2 Mathematical models
2.1 Solid-liquid two-phase mixture model
The settling of whole-tailings in deep-cone thickener is a typical solid-liquid two-phase flow with continuous liquid and discrete solid (whole-tailings particles). Due to a large range of solid PSD, the coupling between solid and liquid is strong and the interactions between solid-liquid two-phase are complex. Therefore, the solid-liquid two-phase mixture model is adopted as the basic mathematical model to simulate the whole-tailings settling in deep-cone thickener in this work. The basic equations of the solid-liquid two-phase mixture model are expressed as follows.
2.1.1 Continuity equation
The continuity equation for the solid-liquid two-phase mixture model is
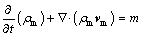 (1)
(1)
where ρm is the density of mixture, which is expressed as . αk is the volume fraction of phase k.
. αk is the volume fraction of phase k. 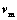 is the mass-averaged velocity, which is
is the mass-averaged velocity, which is 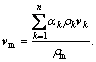
2.1.2 Momentum equation
Summing up the individual momentum equations for all phases, the momentum equation for the solid-liquid two-phase mixture model can be obtained as follows:
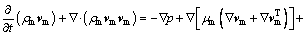
 (2)
(2)
where F is the volume force, n is the number of phases. μm is the viscosity of mixture, which is 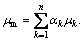
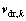 is the drift velocity for secondary phase k, which is
is the drift velocity for secondary phase k, which is 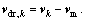
2.1.3 Volume fraction equation for secondary phases
The volume fraction equation for the secondary phase p can be obtained from the continuity equation for p:
 (3)
(3)
2.2 Realizable k-ε turbulence model
In deep-cone thickener, the circulation flow and disturbance flow are formed under the operation of the central cylinder and the mixing rake. The flow pattern is turbulent. Realizable k-ε turbulence model is a swirl correction model, which meets the mathematical limit under Renault pressure and is consistent with the turbulent in physical manner. It is widely used in simulating the cycle, powerful anti-pressure gradient boundary layer, separation as well as recycling works [28]. Studies have shown that the realizable k-ε turbulence model could accurately simulate the flow separation and complex secondary flow. In this work, the realizable k-ε turbulence mode was used to describe the turbulent flow in deep-cone thickener, based on the calculation conditions and contents.
The realizable k-ε turbulence model needs to resolve the equations for turbulent kinetic energy (k) and dissipation rate (ε), which are expressed as follows:

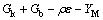 (4)
(4)

 (5)
(5)
where μt is turbulent viscosity coefficient, which is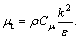 Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients. Gb is the generation of turbulence kinetic energy due to buoyancy. YM represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate. C1ε, C2ε, C3ε and C2 are default constants in Fluent, C1ε=1.44, C2ε=1.90, C3ε=1.30. σk and σε are the turbulent Prandtl numbers for k and ε, respectively, σk=1.0 and σε=1.3.
Gk represents the generation of turbulence kinetic energy due to the mean velocity gradients. Gb is the generation of turbulence kinetic energy due to buoyancy. YM represents the contribution of the fluctuating dilatation in compressible turbulence to the overall dissipation rate. C1ε, C2ε, C3ε and C2 are default constants in Fluent, C1ε=1.44, C2ε=1.90, C3ε=1.30. σk and σε are the turbulent Prandtl numbers for k and ε, respectively, σk=1.0 and σε=1.3.
2.3 Population balance model
It is essential to study the flocculation of deep-cone thickener in tailings particle settling, polymerization and particle breakage of floccules. PBM is a common method for describing the PSD of multiphase flow in discrete phase. The interaction mechanism between solid-phase and liquid-phase was studied in solid-liquid two-phase flow simulation. The impact of solid particle aggregation and fragmentation on solid floccule PSD was studied using PBM.
The Reynolds-averaged form of PBM expression in terms of number density function n(L; x,t) is [29-30]
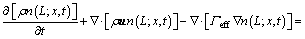
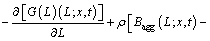
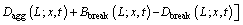 (6)
(6)
where n(L;x,t) is a number density function with the length as the internal coordinate. x is the spatial coordinate variable. u is the mean velocity vector. G(L) is the linear growth rate, and G(L)=dL/dt. Bagg(L;x,t), Dagg(L;x,t), Bbreak(L;x,t), Dbreak(L;x,t) represent the birth and death rates due to aggregation and breakage, respectively. For the sake of simplicity, independent variables x and t will be omitted in the following expressions.

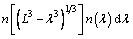 (7)
(7)
 (8)
(8)
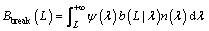 (9)
(9)
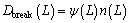 (10)
(10)
where β(L, λ) is the aggregation kernel, ψ(λ) represents the breakage rate, and b(L|λ) is the fragmentation distribution function.
The QMOM is a good choice to deal with aggregation and breakage [31-34]. Compared with other techniques, the QMOM can solve the PBM with good accuracy with a very small number of equations [32, 35]. Thus, the QMOM is very suitable for the computational demand of CFD codes [33, 36].
The QMOM is based on the following Gaussian quadrature approximation:
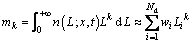 (11)
(11)
where abscissas (Li) and weights (wi) can be obtained through the product-difference (PD) algorithm [32].
During the mixing of the solid-liquid two-phase flow, the aggregation and fragmentation of solid particles are two complex dynamic processes. LUO model [37] and GHADIRI model [38] are adopted to study the aggregation and fragmentation mechanism between whole-tailings particles, respectively.
3 Numerical details
A deep-cone thickener (11 m in diameter) in an enterprise was chosen as a prototype in the present work under the condition of the neglect of transmission device and circulation system. Based on the principle of similitude method, a deep-cone thickener (1.1 m in diameter and 1.6 m in height) was modeled with Fluent 6.3. The schematic diagram of the deep-cone thickener and the rotating rakes is shown in Fig. 1. The feeding inlet (38 mm in diameter) is located at the top of the central cylinder. The overflow outlet condition is approximately modeled through 16 outlet tubes (35 mm in diameter), with each being located at the surface and top of the thickener.
Considering both the practical production process and the principle of similitude method, dimensional data of the deep-cone thickener and physical parameters used in the simulation are given in Table 1. Meanwhile, the particle size distribution curve of whole-tailings is shown in Fig. 2.

Fig. 1 Deep-cone thickener
Table1 Dimensions of deep-cone thickener and physical parameters used in simulation

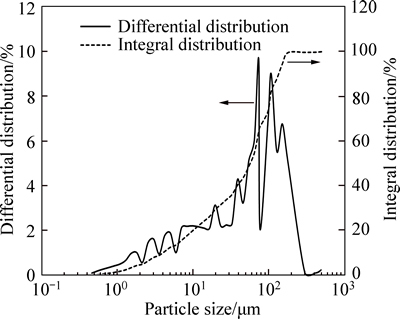
Fig. 2 Particle size distribution of whole-tailings
The mesh was generated based on the preprocessor Gambit. The correlation between the rotating rakes and the thickener was treated as the multi-reference frame. Tetrahedral grids were adopted for both inner and outer zones. In order to verify if the flow field solution is grid independent, the grid independence check has been conducted carefully by means of boundary and gradient adaption. And the grid number of 1026376 was employed for the simulations.
Based on the actual production, the boundary conditions of the inlet is velocity inlet, the boundary conditions of the overflow outlet and underflow outlet are velocity outlet. The 3-D flow filed was obtained by solving the single-phase Reynolds averaged Navier– Stokes equations (RANS). The realizable k-ε turbulence model was adopted. And for the solid wall treatment, the standard wall functions are used. The coupling of velocity and pressure is resolved with SIMPLEC. The momentum equation is discretized with the second order upwind scheme (the relaxation factor is 0.7). The equation for volume fraction is discretized with the QUICK scheme (the relaxation factor is 0.5). The equations for realizable k-ε are discretized with the second order upwind scheme (the relaxation factor is 0.8). The PBM defines the coefficient of aggregation and fragmentation, and it is discretized with the first order upwind scheme at the same time.
4 Results and discussion
4.1 Density distribution in deep-cone thickener
Figure 3 shows the density distribution in deep-cone thickener at 30 min. The result, which is broadly in line with the reported experiments [39-41], shows that the simulation is feasible and applicable. The deep-cone thickener is approximately divided into four zones: liquor zone, free settling zone, hindered settling zone and densification zone. After flowing into the central cylinder, the whole-tailings particles flocculate,aggregate, and settle rapidly due to gravity (almost free settling). When reaching to the hindered settling zone, some particles continue to settle because of their weight, whereas the others could not because of the interference of particles. When flowing into the densification zone, the particles have already been flocculated into compacted floccules, therefore, the settling velocity becomes slow and floccules become more and more compacted. The slurry density increases from the top to the bottom in deep-cone thickener, and it can reach 1484 kg/m3 at underflow outlet, where the mass density of whole-tailings reaches 51.25% by mass fraction.

Fig. 3 Density distribution in deep-cone thickener at 30 min
4.2 Distribution of turbulent kinetic energy
Turbulent kinetic energy is an indicator to evaluate the turbulence development. The variation of turbulent diffusion, which is an important indicator of the mixing capabilities of the turbulence, is proportional to the partial energy of turbulence in fluid. Experiment shows that the distribution of turbulent kinetic energy in the central cylinder is a key factor which influences the flocculation [14]. Proper turbulent kinetic energy will effectively promote the mixing and adsorption of flocculant, particles collision as well as flocculation growth. However, exorbitant high turbulent kinetic energy will strongly increase the shear of the fluid and destroy the formed flocculation. The distribution of turbulent kinetic energy in deep-cone thickener at 33 min is shown in Fig. 4.
As shown in Fig. 4, the turbulent kinetic energy in the periphery of rotating rake is stronger than that in the center of the deep-cone thickener. Exorbitant turbulent kinetic energy is harmful to the stretching and shaping of the flocculation, because it destroys the structures of the flocculation. Furthermore, the intra-aggregate water trapped inside the aggregate structures would also be discharged. The efficiency of dewatering of the whole-tailings is improved as a result. As seen from Figs. 4(b)-(d), the turbulent kinetic energy is the strongest in the section of the feeding inlet and reduces gradually from the section to the outer-side of the central cylinder. Meanwhile, the distribution of the turbulent kinetic energy becomes more and more uniform.

Fig. 4 Distribution of turbulent kinetic energy in deep-cone thickener at 33 min:
As a result, the strong turbulent kinetic energy at the section of the feed inlet contributes to the mixing of slurry and flocculants, and promotes the flocculation extension and formation. However, the low and uniform distribution of turbulent kinetic energy at the bottom of the central cylinder produce a small shear rate of slurry which has a small chance to damage the flocculation.
4.3 Whole-tailings floccules distribution
4.3.1 Floccules particle size distribution
The PSD of the whole-tailings floccules particle in deep-cone thickener is predicted with CFD-PBM. Figure 5 shows the PSD of the floccules at 35 min. It can be seen that for most of floccules, the particle size of floccules are in the range of 1500-2000 μm, while only a small amount are larger than 2600 μm. What’s more, the PSD of floccules particle in number density is in good agreement with the PSD in percentage which comes from experiment. This means that the simulation is of high credibility and reliability.
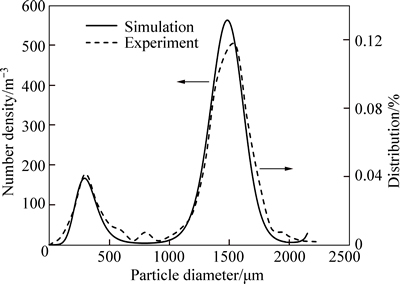
Fig. 5 Floccules particle size distribution in deep-cone thickener at 35 min
4.3.2 Spatio-temporal changes in PSD of whole-tailings floccules
1) Sauter mean diameter of whole-tailings floccules
When studying the spatio-temporal changes in whole-tailings floccules mean diameter, the Sauter mean diameter can be expressed as follows:
 (12)
(12)
where d32 is the Sauter mean diameter of whole-tailings floccules. Nk and dk are the number and diameter of the k-th floccule, respectively.
2) PSD of floccules at different moments at bottom-outlet
Figures 6 and 7 show the PSD of floccules at different moments at the bottom-outlet. In Fig. 6, the horizontal axis is the particle size of whole-tailings floccules, and the vertical axis is the number density of whole-tailings floccules. It can be seen from Fig. 6 that the number of small floccules declines over time, while the number of large floccules increases at first and then declines. The PSD at 30 min, 33 min and 35 min are almost the same. In other words, the PSD becomes stable at this moment. As seen from Fig. 7, the Sauter mean diameter of whole-tailings floccules increases at first and then declines slightly until reaching a stable status. In the initial stage, the floccules continue to grow and settle due to gravity. However, due to the agitation and shear of rotating rakes, large floccules break into small floccules. That’s why the number of large floccules increases at first and then declines with time.
During the first 15 min, the Sauter mean diameter of whole-tailings floccules and the number of floccules with large particle size increase sharply. This illustrates that the flocculation is not stable and the particle size distribution changes significantly, which suggests that the underflow outlet should be turned off until the flocculation in deep-cone thicker becomes stable approximately in practice. In other words, the intermittent flocculation settlement should be conducted before the dynamic settling. In the meantime, the necessity and rationality of the circulation system at the bottom of the deep-cone thicker are illustrated.

Fig. 6 Floccules particle size distribution at different moments at bottom-outlet

Fig. 7 Floccules Sauter mean diameter distribution at different moments at bottom-outlet
3) PSD of floccules at different depths at 35 min
Figures 8 and 9 show the PSD of floccules at different depths at 35 min. In Fig. 8, the horizontal axis is the particle size of whole-tailings floccules, the vertical axis is the number density of whole-tailings floccules, and h is the distance to the cross section of the feeding inlet. The cross section of the overflow outlet, the bottom outlet of central cylinder, and underflow outlet are at h=104.5 mm, h=219 mm and h=1533 mm, respectively. It is shown from Fig. 8 that the curves of the PSD at different depths are similar. The number of floccules with large particle size increases and the range of distribution continually widens with the increase in depth. The PSD at the top is narrower than that at the lower part, which is mainly because the upper floccules cannot be complemented effectively in a short period of time and the large floccules are settled down due to gravity. With the increase in depth, the loss of floccules can be effectively supplied by the constant settling of upper floccules. That’s why the PSD curve becomes widened, and also both the number of large floccules and the Sauter mean diameter of the whole-tailings floccules continue to increase.
Although the Sauter mean diameter of the whole-tailings floccules increases with the increase of depth, the proportion of the increase and the changes in the distribution range are not significant. This indicatesthat the flocculation mainly occurs in the central cylinder. In the central cylinder, the Sauter mean diameter of the whole-tailings floccules increases above h=104.5 mm (the cross section of the overflow outlet) and then declines until h=219 mm (the bottom outlet of the central cylinder). This indicates that the flocculation occurs mainly at the upper part of the central cylinder. The Sauter mean diameter in the cross section of the feeding inlet is 2138 μm which expands approximately 40 times of the average diameter of whole-tailings particles (58.3 μm). This indicates that the strong flocculation mainly occurs in the feeding inlet.

Fig. 8 Floccules particle size distribution at different depths at 35 min
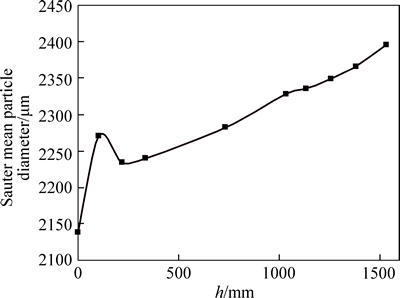
Fig. 9 Floccules Sauter mean diameter distribution at different depths at 35 min
5 Conclusions
1) The mathematical models used in this simulation can accurately reflect the concentration variation law of the whole-tailings flocculation in deep-cone thickener.
2) At bottom-outlet of the deep-cone thickener, the number of small floccules declines over time, while the number of large floccules increases at first and then declines.
3) The number of large floccules increases and PSD curve continually widens with the increase in depth.
4) The Sauter mean diameter of the whole-tailings floccules increases at first, then declines and finally reaches a stable value over time, while the value continually increases with the increase of depth.
5) The flocculation of the whole-tailings mainly occurs in the cross section of feed inlet in the central cylinder in deep-cone thickener.
This study is only the initial attempt using CFD- PBM to simulate the whole-tailings flocculation and settling in a deep-cone thickener. Further study will focus on the improvements of the model, such as the nucleation and growth of the whole-tailings, and the circulation system of deep-cone thickener.
Nomenclature
Bagg(L;x,t)
Birth rate due to aggregation
Bbreak(L;x,t)
Birth rate due to breakage
b(L|λ)
Fragmentation distribution function
C
Default constants in Fluent
D
Diameter, m
dav
Average diameter, μm
d2
Sauter mean particle diameter, μm
Dagg(L;x,t)
Death rate due to aggregation
Dbreak(L;x,t)
Death rate due to breakage
F
Volume force, N
Gk
Generation of turbulence kinetic energy due to mean velocity gradients
Gb
Generation of turbulence kinetic energy due to buoyancy
G(L)
Linear growth rate
H
Height, m
K
Turbulence kinetic energy
Li
Abscissas
m
Mass, kg
mk
Moment
n
Number of phases
n(L;x,t)
Number density function, m-4
N
Rotational speed, r/min
u
Mean velocity vector, m
Q1
Feed flow, m3/s
Q2
Underflow, m3/s
Q3
Overflow, m3/s
vm
Mass-averaged velocity, m/s
vdr,k
Drift velocity for secondary phase k, m/s
vdr,p
Drift velocity for secondary phase p, m/s
wi
Weight
x
Spatial coordinate variable, m
YM
Contribution of fluctuating dilatation in compressible turbulence to overall dissipation rate
αk
Volume fraction of phase k
αp
Volume fraction of phase p
β(L,λ)
Aggregation kernel
ψ(λ)
Breakage rate
ρ
Density, kg/m3
ρm
Mixture density, kg/m3
ρs
Density of solid, kg/m3
ρl
Density of liquid (water), kg/m3
ρn
Mass concentration,%
ρp
Density of phase p, kg/m3
μ
Dynamic viscosity of fluid, kg/(m·s)
μm
Viscosity of mixture, kg/(m·s)
μt
Turbulent viscosity, kg/(m·s)
μs
Turbulent viscosity of solid, kg/(m·s)
μl
Turbulent viscosity of liquid (water), kg/(m·s)
ε
Turbulence energy dissipation rate, m2/s3
σ
Surface tension coefficient, N/m
σk
Turbulent Prandtl numbers for k
σε
Turbulent Prandtl numbers for ε
References
[1] GRABINSKY M W. In situ monitoring for ground truthing paste backfill designs [C]// Proceedings of the 13th International Seminar on Paste and Thickened Tailings. Perth: Australian Centre for Geomechanics, 2010: 85-98.
[2] ZHANG Qin-li, ZHOU Deng-hui, WANG Xin-min, ZHAO Jian-wen. Experimental study on flocculating sedimentation of ultra-fine unclassified tailings [J]. J Guangxi Univ: Nat Sci Ed, 2013, 38(2): 452-455. (in Chinese)
[3] B URGERA R, DAMASCENOB J J R, KARLSENC K H. A mathematical model for batch and continuous thickening of flocculated suspensions in vessels with varying cross section [J]. Int J Miner Process, 2004, 73: 183-208.
URGERA R, DAMASCENOB J J R, KARLSENC K H. A mathematical model for batch and continuous thickening of flocculated suspensions in vessels with varying cross section [J]. Int J Miner Process, 2004, 73: 183-208.
[4] USHER S P, SPEHAR R, SCALES P J. Theoretical analysis of aggregate densification: Impact on thickener performance [J]. Chem Eng J, 2009, 151(1): 202-208.
[5] USHER S P, SCALES P J. Steady state thickener modelling from the compressive yield stress and hindered settling function [J]. Chem Eng J, 2005, 111(2): 253-261.
[6] SPEHAR R, KIVITI-MANOR A, FAWELL P, USHER S P, RUDMAN M, SCALES P J. Aggregate densification in the thickening of flocculated suspensions in an un-networked bed [J]. Chem Eng Sci, 2015, 122: 585-595.
[7] ESWARAIAH C, BISWAL S K, MISHRA B K. Settling characteristics of ultrafine iron ore slimes [J]. Int J Miner Metall Mater, 2012, 19(2): 95-99.
[8] DU Jian-hua, PUSHKAROVA R A, SMART R S C. A cryo-SEM study of aggregate and floc structure changes during clay settling and raking processes [J]. Int J Miner Process, 2009, 93(1): 66-72.
[9] SELOMUYA C, JIA X, WILLIAMS R A. Direct prediction of structure and permeability of flocculated structures and sediments using 3D tomographic imaging [J]. Chem Eng Res Des, 2005, 83(7): 844-852.
[10] GARRIDO P, BURGOS R, CONCHA F, BURGER F. Software for the design and simulation of gravity thickeners [J]. Miner Eng, 2003, 16(2): 85-92.
[11] BURGOS R, CONCHA F. Further development of software for the design and simulation of industrial thickeners [J]. Chem Eng J, 2005, 111(2): 135-144.
[12] KAHANE R, NGUYEN T, SCHWARZ M P. CFD modelling of thickeners at Worsley alumina Pty Ltd [J]. Appl Math Modeling, 2002, 26(2): 281-296.
[13] WHITE R B, SUTALO I D, NGUYEN T. Fluid flow in thickener feedwell models [J]. Miner Eng, 2003, 16(2): 145-150.
[14] OWEN A T, NGUYEN T V, FAWELL P D. The effect of flocculant solution transport and addition conditions on feedwell performance in gravity thickeners [J]. Int J Miner Process, 2009, 93(2): 115-127.
[15] TANGUAY M, FAWELL P, ADKINS S. Modelling the impact of two different flocculants on the performance of a thickener feedwell [J]. Appl Math Modelling, 2014, 38: 4262-4276.
[16] ZHU Gui-hua, ZHANG Yu-zhu, REN Ji-liang, QIU Tuan-hui, WANG Tao. Flow simulation and analysis in a vertical- flowsedimentationtank [C]// 2012 International Conference on Future Energy, Environment, andMaterials. Energy Procedia, 2012, 16: 197-202.
[17] KAHANE R B, SCHWARZ M P, JOHNSTON R M. Residue thickener modelling at Worsley alumina [C]// International Conference on CFD in Mineral & Metal Processing and Power Generation. Melbourne: CSIRO, 1997: 109-118.
[18] NGUYEN T, HEATH A, WITT P. Population balance-CFD modelling of fluid flow, solids distribution and flocculation in thickener feedwells [C]// Fifth International Conference on CFD in the Process Industries. Melbourne: CSIRO, 2006: 1-6.
[19] NOPENS I,BIGGS C A, de CLERCQ B, GOVOREANU R, WIL N B M, LANT P, VANROLLEGHEM P A. Modelling the activated sludge flocculation process combining laser light diffraction particle sizing and population balance modelling (PBM) [J]. Water Sci Technol, 2002, 45(6): 41-49.
N B M, LANT P, VANROLLEGHEM P A. Modelling the activated sludge flocculation process combining laser light diffraction particle sizing and population balance modelling (PBM) [J]. Water Sci Technol, 2002, 45(6): 41-49.
[20] HEATH A R, PETER T L K. Combined population balance and CFD modeling of particle aggregation by polymeric flocculants [C]// Third International Conference on CFD in the Minerals and Process Industries. Melbourne: CSIRO, 2003: 339-344.
[21] WEI H. Application of computational fluid dynamics techniques to the modelling of precipitation processes [D]. UK: UMIST, 1997.
[22] GARSIDE J, WEI H. Pumped stirred and maybe precipitated: simulation of precipitation process using CFD [J]. Acta Polytech Scand, Chem Technol Metall Ser, 1997, 245: 9-15.
[23] CHENG Jing-cai, YANG Chao, MAO Zai-sha. CFD-PBE simulation of premixed continuous precipitation incorporating nucleation, growth and aggregation in a stirred tank with multi-class method [J]. Chem Eng Sci, 2012, 68(1): 469-480.
[24] JAWORSKI Z, NIENOW A W. CFD modelling of continuous precipitation of barium sulphate in a stirred tank [J]. Chem Eng J, 2003, 91: 167-174.
[25] WANG Zheng, MAO Zai-sha, YANG Chao, SHEN Xiang-qian. Computational fluid dynamics approach to the effect of mixing and draft tube on the precipitation of barium sulfate in a continuous stirred tank [J]. Chin J Chem Eng, 2006, 14(6): 713-722.
[26] VICUM L, MAZZOTTI M. Multi-scale modeling of a mixing-precipitation process in a semibatch stirred tank [J]. Chem Eng Sci, 2007, 62: 3513-3527.
[27] CHENG Jing-cai, YANG Chao, MAO Zai-sha, ZHAO Cheng-jun. CFD modeling of nucleation, growth, aggregation, and breakage in continuous precipitation of barium sulfate in a stirred tank [J]. Ind Eng Chem Res, 2009, 48(15): 6992-7003.
[28] YAKHOT V, ORSZAG S A. Renormalization group analysis of turbulence [J]. J Sci Comput, 1986, 1(1): 3-51.
[29] RANDOLPH A D, LARSON M A. Theory of particulate processes [M]. 2nd ed. San Diego, CA: Academic Press, 1988: 41-63.
[30] RAMKRISHNA D. Population balance: Theory and application to Particulate Systems in Engineering [M]. New York: Academic Press, 2000: 7-45.
[31] MARCHISIO D L, VIGIL R D, FOX R O. Quadrature method of moments for aggregation-breakage processes [J]. J Colloid Interface Sci, 2003, 258: 322-334.
[32] MCGRAW R. Description of aerosol dynamics by the quadrature method of moments [J]. Aerosol Sci Technol, 1997, 27(2): 255-265.
[33] MARCHISIO D L, VIGIL R D, FOX R O. Implementation of the quadrature method of moments in CFD codes for aggregation- breakage problems [J]. Chem Eng Sci, 2003, 58: 3337-3351.
[34] MARCHISIO D L, PIKTURNA J T, FOX R O, VIGIL R D. Quadrature method of moments for population-balance equations [J]. AIChE J, 2003, 49(5): 1266-1276.
[35] MARCHISIO D L, SOOS M, SEFCIK J, MORBIDELLI M. Role of turbulent shear rate distribution in aggregation and breakage processes [J]. AIChE J, 2006, 52(1): 158-173.
[36] WANG L, MARCHISIO D L, VIGIL R D, FOX R O. CFD simulation of aggregation and breakage processes in laminar Taylor-Couette flow [J]. J Colloid Interface Sci, 2005, 282: 380-396.
[37] LUO He-an. Coalescence, breakup and liquid circulation in bubble column reactors [D]. Trondheim: Norwegian Institute of Technology, 1993.
[38] GHADIRI M, ZHANG Z. Impact attrition of particulate solids. Part 1: A theoretical model of chipping [J]. Chem Eng Sci, 2002, 57: 3659-3669.
[39] TAO D, PAREKH B K, ZHAO Yue-ming, ZHANG P. Pilot-scale demonstration of deep coneTM paste thickening process for phosphatic clay/sand disposal [J]. Sep Sci Technol, 2008, 45(10): 1418-1425.
[40] WU Ai-xiang, SUN Ye-zhi. Granular dynamic theory and its applications [M]. Beijing: Metallurgical Industry Press, 2008: 135-138.
[41] LI Hui, WANG Hong-jiang, WU Ai-xiang, JIAO Hua-zhe, LIU Xiao-hui. Pressure rake analysis of deep cone thickeners based on tailings’ settlement and rheological characteristics [J]. J Univ Sci Technol Beijing, 2013, 35(12): 1553-1558. (in Chinese)
(Edited by YANG Bing)
Foundation item: Project(51174032) supported by the National Natural Science Foundation of China; Project(NCET-10-0225) supported by the Program for New Century Excellent Talents in University, China; Project(FRF-TP-09-001A) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2015-07-20; Accepted date: 2015-12-04
Corresponding author: LI Cui-ping, Associate Professor, PhD; Tel: +86-13691563136; E-mail: cpli@ustb.edu.cn

