J. Cent. South Univ. Technol. (2009) 16: 0073-0079

DOI: 10.1007/s11771-009-0012-8

Electron bandstructure of kaolinite and its mechanism of flotation using dodecylamine as collector

XIA Liu-yin(夏柳荫)^{1, 2}, ZHONG Hong(钟 宏)², LIU Guang-yi(刘广义)², LI Xin-gang(李鑫钢)¹

(1. School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China;

2. School of Chemistry and Chemical Engineering, Central South University, Changsha 410083, China)

Abstract: The bulk electronic structure of kaolinite (001) plane was studied with quantum mechanical calculations. The CASTEP parameterization of ultrasoft pseudopotentials without core corrections was used to optimize the structure of kaolinite bulk and slab models. The results show that Fermi energy of kaolinite (001) plane is 3.05 eV, and the band gap is 4.52 eV. The partial density of states (PDOS) of kaolinite (001) plane indicates that Al—O and Si—O bonds on the mineral surface are highly polar. The oxygen atoms of hydroxyl groups in surface layer are capable of forming hydrogen bond with the head group of cationic collectors. The properties of dodecylamine (DDA) cation were also calculated by density function theory (DFT) method at B3LYP/6-31G (d) level for illuminating the flotation processes of kaolinite. Besides the electrostatic attraction, the mechanism between kaolinite and DDA is found to be hydrogen bonds under acidic condition.

Key words: kaolinite; electron bandstructure; flotation; quantum mechanical calculations

1 Introduction

Kaolinite, Al₂Si₂O₅(OH)₄, is a layered alumino- silicate with a dioctahedral 1?1 layer structure consisting of an octahedral aluminum hydroxide sheet and a tetrahedral silica sheet [1-2]. It is the major silica- bearing clay in diasporic bauxite ores in China. Many flotation experts have studied kaolinite flotation with various collectors [3-6]. To fully understand the flotation process of kaolinite, researchers usually perform flotation experiments, zeta potential measurements, and FTIR spectral analysis. Generally, the interaction between the collector cations and the negative charged mineral surfaces is mainly considered electrostatic forces. However, the interaction mechanisms between the cationic collectors and the mineral surfaces have not yet been fully established. In some circumstances, the hydrogen bonds were presumed to be existence due to the anomalous flotation behavior of minerals. One of the reasons for the limited knowledge of what happens on the mineral surface is the difficulty to perform in situ measurements.

One approach to a better understanding of the mineral surfaces is to model the structure of kaolinite surfaces. Much effort has been dedicated to the modeling at the atomic level, due to the important advances in the theory and computer technology in recent years [7-8]. COLLINS and CATLOW [9] and BOSENICK et al [10] reported the modeling of layered phyllosilicates with high interlayer charge, such as muscovite, where the models of empirical interatomic potentials were applied. LASAGA [7], KUBICKI et al [11-12], and SAINA- DIAZ et al [13] employed quantum-mechanical studies on clusters or molecular models of the infinite structures with interesting results. SHERMAN [14], SMRCOK and BENCO [15], WINKLER et al [16-17], and BRIDGEMAN et al [18] used the first principle quantum techniques, based on density function theory (DFT) with periodic boundary conditions that avoid the edge effects associated with the cluster approach.

The modeling, however, cannot give a specific explanation for flotation processes that do occur on mineral surfaces. One of the aims of this work was to model the electronic structure with quantum mechanical method to understand the physical and chemical properties of the planes and to know the properties of bulk material. This is based on the work of EDELBRO  et al [19], who studied the electron bandstructures of sphalerite, pyrite and chalcopyrite for illuminating the flotation processing. Furthermore, we explained the mechanism of collector molecules adsorbed on kaolinite surfaces, and understood the flotation processes that take place on mineral surfaces on an atomic scale.

2 Computational methods

Kaolinite crystal structure was established from a two-layer aluminosilicate. Optimizations and surface relaxations were calculated using the pseudopotential planewave density functional theory (PPW-DFT) method, as implemented in CASTEP (a calculation module in the software of Materials Studio) [20]. The generalized gradient approximation (GGA) and generalized gradient local spin approximation (GGS) were applied using the Perdew-Wang parameterization [21] of the exchange- correlation functional, which was modified to work with planewave calculations [22]. We used the CASTEP parameterization of ultrasoft pseudopotentials [23] without core corrections to optimize the structure of kaolinite bulk and slab models. Pseudopotentials were generated using the local density approximation and local spin density approximation (LDA/LSDA), meaning that the screening effect of the core electrons was modelled using LDA/LSDA, whereas the screening effect of the valence electrons was modeled using GGA/GGS. This approach was validated previously [24] and successfully applied to structure optimizations of 2?1 phyllosolicates [25-26]. In this calculation, energy tolerance is 2.721×10^-4 eV, the maximum force tolerance is 0.544 eV/nm, and self consisting field (SCF) tolerance is 1.00×10^-6.

Calculations of the collector cations were made by using the Gaussian 03 [27] and Chemoffice2005 program. The initially molecular modeling of cationic collector molecule was optimized by MM2 and MP3 methods. The obtained geometries were further optimized and calculated with DFT methods at the B3LYP level using 6-31G (d) basis set, and the single point energies were corrected by means of the full counterpoise technique.

3 Results

3.1 Structure of kaolinite

Kaolinite is a dioctahedral 1?1 layered aluminosilicate with the ideal chemical composition Al₂Si₂O₅(OH)₄, consisting of alternating layers of tetrahedral silicates and octahedral aluminum oxy- hydroxides. Two layers are covalently bound together through common oxygen atoms, forming a layer- structured repeating unit. Hydrogen bonds between the hydroxyl ions of octahedral aluminum oxyhydroxides and the oxygen atoms of tetrahedral silicates hold the repeating units together. The space group symmetry of kaolinite is C1. Refinement of the structure from single- crystal synchrotron data provides the unit-cell parameters a=0.514 90 nm, b=0.893 35 nm, c=0.738 44 nm, α= 91.930?, β=105.042?, γ=89.791? [28]. Fig.1 shows the crystal structure with all three surface hydroxyl groups in a primitive cell oriented approximately vertically with respect to the layer, indicating the formation of three- interlayer hydrogen bonds.

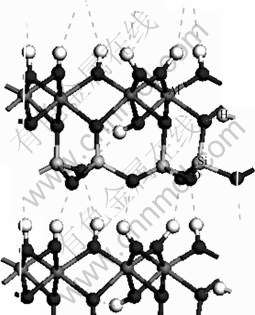
Fig.1 Experimental structure of kaolinite

The cleavage of kaolinite along (001) planes between repeating units by comminution is anticipated to break the hydrogen bonds on the cleaved surfaces, i.e. (001) plane [29-31]. Besides its basal planes, kaolinite is also cleaved along (010), (110) and (100) planes to create edges, where Al—OH or Al—O bonds exist. Table 1 lists the number and types of the broken bonds, and Fig.2 shows the optimized and relaxed planes of (001), (010), (110) and (100). As seen from Fig.2, heterogeneous bonds are broken down on different planes. The basal face is believed to have hydrogen bonds, while the edge planes mainly consist of Al—O and Si—O bonds. Thus the characteristics of kaolinite surfaces are determined by the properties of (001) planes when kaolinite is cleaved.

Table 1 Number and type of bonds broken on kaolinite planes

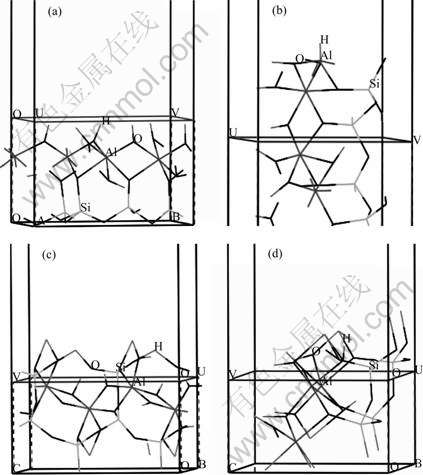
Fig.2 Surfaces of kaolinite: (a) (001) Plane; (b) (010) Plane; (c) (110) Plane; (d) (100) Plane

3.2 Electron bandstrucure of kaolinite

By simulating the kaolinite crystal bulk and the slab models, the electron bandstructure and the partial density of states (PDOS) for kaolinite (001) plane as well as total and atom-decomposed PDOS were calculated. The results are shown in Figs.3 and 4, respectively.

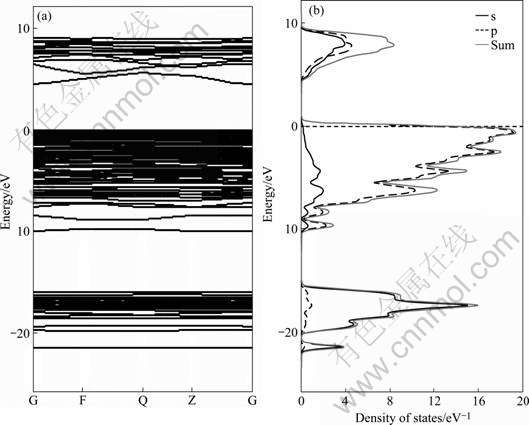
Fig.3 Bandstructures (a) and PDOS (b) of kaolinite (001) plane (zero of energy was set at the highest occupied state)

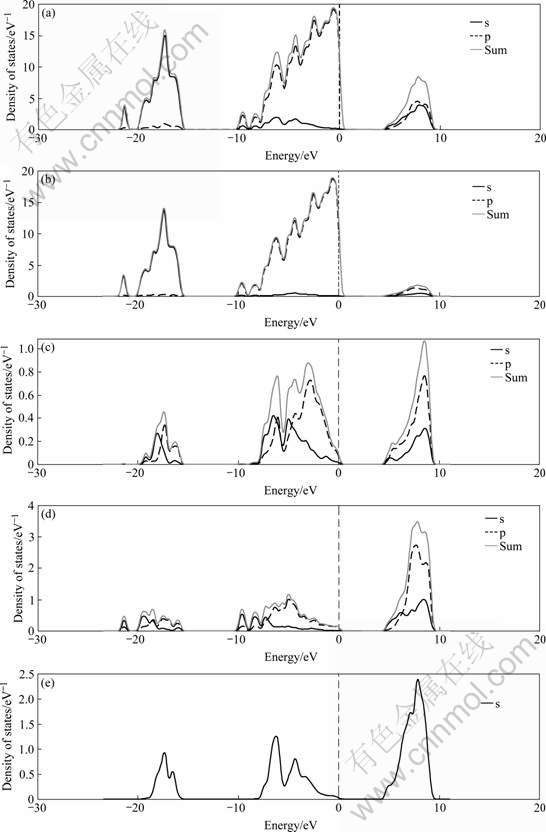
Fig.4 Total and atom-decomposed DOS of kaolinite (001) plane: (a) total DOS; (b) O atomic DOS; (c) Al atomic DOS; (d) Si atomic DOS; (e) H atomic DOS

Fig.3 presents the energy bandstructure and the density of states curve calculated by the CASTEP parameterization of ultrasoft pseudopotentials method. The Fermi energy at 3.05 eV is taken to be zero. The band gap of kaolinte is 4.52 eV. Kaolinite primitive cell consists of nine oxygen atoms, so bands 1-18 located in the interval from -21.94 to -16.43 eV come from the O 2s quasi-core band. The O 2p valence bands, 19-72, are entirely filled, and the width of the O 2p band yields 15.87 eV. The upper 12 bands, of which the bands 73-84, are partially filled, consist of a mixture of orbits from all atoms.

By comparing Fig.3 with Fig.4, the first clear feature is that almost all the valence charges are associated with oxygen atoms, suggesting a highly polar character of the Al—O and Si—O bonds. Similarly, the bands near the Fermi level are almost from the O 2p orbit. The highest occupied molecular orbit (HOMO) band energy reveals the possibility of transferring an electron to the cationic group. However, the tendency of reactivity is little because of the smooth bands below the Fermi level. The bandstructure and PDOS of the kaolinite plane indicate that the oxygen atoms in hydroxyl groups on the aluminum octahedral surface layer are the reactive sites in kaolinite.

3.3 Mechanism of kaolinite flotation using DDA

Isomorphous substitution of various cations in the octahedral and tetrahedral sheet results in a net negative charge of the layers. This charge can be compensated by the presence of additional cations. Thus cationic surfactants for the kaolinite flotation are proved to be effective. In this work, we chose dodecylamine (DDA), the earliest reported cationic collector for kaolinite, as a collector to explain the mechanism of flotation.

The optimized geometry used in DFT calculation of DDA cation is revealed in Fig.5. The HOMO and the lowest unoccupied molecular orbit (LUMO) energies of the species, some selected bond distances, and atomic charges are described in Table 2.

Table 2 Frontier orbital eigenvalues, some selected bond distances and Mulliken charges of reagent at B3LYP/6-31G (d) level

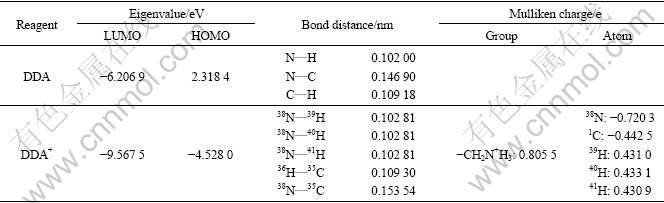
Fig.5 Optimized geometry of DDA cation at B3LYP/6-31G (d) level

The computational frontier orbital eigenvalues (HOMO, LUMO) of the collectors listed in Table 2 seem to be very difficulty in forming covalent bond with metal ions on mineral surfaces. Firstly, the HOMO eigenvalues of DDA cation are very low, and its electron-donating power is very weak. The HOMO is constituted by p_x or p_z-orbits of carbon atoms that have full-filled valence and no chance to offer p-orbit electron to other atoms. The LUMO eigenvalues of DDA cation are also low and the LUMO compositions are mainly composed of s-orbit of N, C and H atoms, which means the LUMO cannot accept feedback electron to form π-bond. Furthermore, the calculation results of kaolinite show that the direct and indirect band gap of kaolinte is 4.52 eV. This also means that DDA cation has difficulty in forming a covalent bond with the aluminum atom on mineral surface. Mulliken charge of group —CH₂N⁺H₃ is  0.805 5, indicating that DDA cation can be easily adsorbed on the negatively charged mineral surface through physical electrostatic attraction. This is consistent with previous experimental studies [32-34].

The N and H atomic Mulliken charges show that N atoms are negatively charged in both regents. It is obvious that the charge of N in DDA cation is much negative. The N—H bond length in DDA cation is  0.102 81 nm, which is much longer than N—H bond length of 0.102 00 nm in DDA molecules. This means that the N—H bonds in —NH₃ group of DDA cation may form the N—H…^-O hydrogen bond with the hydroxyl on the mineral surfaces. This is corresponding to the previous analysis that O atom as the active site on the mineral surfaces may bond with collector molecules.

4 Discussion

The flotation behavior of kaolinite with DDA as a collector was studied by JIANG et al [35]. The results show that the floatability of kaolinite decreases signi- ficantly at pH＞5. This can be explained by the mechanism of kaolinite flotation summarized in this work.

The charge on surfaces of kaolinite depends on the pH value of solution. The relationship between the concentration of aqueous Si and Al species in kaolinite solution and pH value is shown in Fig.6. The main Al species and the main Si species in water-kaolinite interface at different pH values are shown in Fig.7 and Table 3. It is evident that, DDA is mainly present in the form of (C₁₂H₂₅NH₃⁺)₂ and C₁₂H₂₅NH₃⁺ cationic ions in aqueous solution and kaolinite presents Al—OH, Al—O^-, Si—OH and Si—O^- species on the surface in the pH value from 5.5 to 8.5. As a result, (C₁₂H₂₅NH₃⁺)₂ and C₁₂H₂₅NH₃⁺ cationic ions can easily adsorb on kaolinite through electrostatic effect. As for pH＞8.5, the electrostatic attraction can be weaken by superfluous OH^- in pulp.

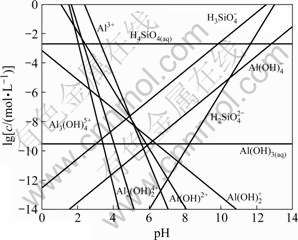
Fig.6 Concentration distribution of aqueous Si or Al species in kaolinite solution as function of pH value

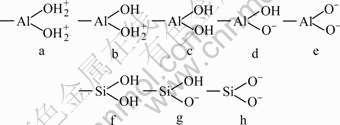
Fig.7 Probable compositions in water-kaolinite interface

Table 3 Probable compositions of kaolinite at different pH values

Under acidic condition, the apex oxygen atoms in the silica tetrahedral will be hydrolyzed and form dangling hydroxyl groups and naked O anions on the surface to provide extra hydrogen bonding sites. In this circumstance, the hydrogen bond formed between the collector and the mineral surfaces is the dominate reason for adsorption. With increasing pulp pH, the extra hydrogen bonding sites decrease, resulting in the depressed kaolinite recovery accordingly.

5 Conclusions

(1) The quantum mechanical calculations of the electronic structure of kaolinite (001) plane show that the oxygen atoms of hydroxyl groups in the aluminum octahedral are the most active sites of kaolinite, and are capable of forming hydrogen bonds with the head group of cationic collectors.

(2) Combining DFT calculations of DDA cation properties with solution chemistry analysis of kaolinite in solution, a detailed atomic-scale understanding of floatation processing is obtained. Physical electrostatic effect and hydrogen bond mainly account for the mechanism of the cations adsorption on mineral surfaces. This not only felicitously explains the flotation behavior of kaolinite with DDA, but also proves the calculation results in this work.

References

[1] AKIBA E, HAYAKAWA H, HAYASHI S, MIYAWAKI R, TOMURA S, SHIBASAKI Y, IZUMI F, ASANO H, KAMIYAMA T. Structure refinement of synthetic deuterated kaolinite by rietveld analysis using time-of-flight neutron powder diffraction data [J]. Clays and Clay Minerals, 1997, 45(6): 781-788.

[2] BISH D L, VON DREELE R B. Rietveld refinement of non- hydrogen atomic positions in kaolinite [J]. Clays and Clay Minerals, 1989, 37(4): 289-296.

[3] CAO Xue-feng, HU Yue-hua, JIANG Yu-ren. Flotation mechanism of aluminum silicate minerals with N-dodecyl-1, 3-diaminopropane [J]. Chinese Journal of Nonferrous Metals, 2001, 11(4): 693-696. (in Chinese)

[4] LI Hai-pu, HU Yue-hua, JIANG Yu-ren. Interaction mechanism between modified starches and aluminum-silicate minerals [J]. Chinese Journal of Nonferrous Metals, 2001, 11(4): 697-681. (in Chinese)

[5] ZHAO Shi-min, WANG Diang-zuo, HU Yue-hua. Flotation of aluminosilicates using N-(2-aminoethyl)-1-naphthaleneacetamide [J]. Minerals Engineering, 2003, 16(10): 1031-1033.

[6] ZHAO Shi-min, WANG Dian-zuo, HU Yue-hua. A series of aminoamides used for flotation of kaolinite [J]. Journal of University of Science and Technology Beijing, 2005, 12(3): 208-212.

[7] LASAGA A C. Fundamental approaches in describing mineral dissolution and precipitation rates [R]. Washington DC: Mineralogical Society of America, 1995.

[8] SAUER J, UGLIENGO P, GARRONE E, SAUNDERS V R. Theoretical study of van der Waals complexes at surface sites in comparison with the experiment [J]. Chemical Reviews, 1994, 94(7): 2095-2160.

[9] COLLINS D R, CATLOW C R. Computer simulations of structures and cohesive properties of micas [J]. American Mineralogist, 1992, 77(11/12): 1172-1181.

[10] BOSENICK A, DOVE M T, MYERS E R, PALIN E J, SAINZ-DIAZ C I, GUITON B S, WARREN M C, CRAIG M S, REDFERN S A T. Computational methods for the study of energies of cation distributions: Applications to cation-ordering phase transitions and solid solutions [J]. Mineralogical Magazine, 2001, 65(2): 193-219.

[11] KUBICKI J D, BLAKE G A, APITZ S E. Ab initio calculations on aluminosilicate Q3 species: Implications for atomic structures of mineral surfaces and dissolution mechanisms of feldspars [J]. American Mineralogist, 1996, 81(7/8): 789-799.

[12] KUBICKI J D, APITZ S E. Molecular cluster models of aluminum oxide and aluminum hydroxide surfaces [J]. American Mineralogist, 1998, 83(9/10): 1054-1066.

[13] SAINZ-DIAZ C I, TIMON V, BOTELLA V, HERNANDEZ- LAGUNA A. Isomorphous substitution effect on the vibration frequencies of hydroxyl groups in molecular cluster models of the clay octahedral sheet [J]. American Mineralogist, 2000, 85(7/8): 1038-1045.

[14] SHERMAN D M. Hartree-Fock band structure, equation of state, and pressure-induced hydrogen bonding in brucite, Mg(OH)₂ [J]. American Mineralogist, 1991, 76(9/10): 1769-1772.

[15] SMRCOK L, BENCO L. Ab initio periodic Hartree-Fock study of lizardite [J]. American Mineralogist, 1996, 81(11/12): 1405-1412.

[16] WINKLER B, MILMAN V, PAYNE M C. Ab initio total energy studies of minerals using density functional theory and the local density approximation [J]. Mineralogical Magazine, 1995, 59(4): 589-596.

[17] WINKLER B, MILMAN V, HYTHA M, PICKARD C, MILMAN V, WARREN M C. Theoretical investigation of bonding in diaspore [J]. European Journal of Mineralogy, 2001, 13(2): 343-349.

[18] BRIDGEMAN C H, BUCKINGHAM A D, SKIPPER N T, PAYNE M C. Ab initio total energy study of uncharged 2:1 clays and their interaction with water [J]. Molecular Physics, 1996, 89(3): 879-888.

[19] EDELBRO R, SANDSTROM A, PAUL J. Full potential calculations on the electron band structures of sphalerite, pyrite and chalcopyrite [J]. Applied Surface Science, 2003, 206(1/4): 300-313.

[20] PAYNE M C, TETER M P, ALLAN D C. Iterative minimization techniques for ab initio total-energy calculations: Molecular dynamics and conjugate gradients [J]. Reviews of Modern Physics, 1992, 64(4): 1045-1097.

[21] PERDEW J P, WANG Y. Accurate and simple analytic representation of the electron-gas correlationenergy [J]. Physical Review B, 1992, 45(13): 13244-13249.

[22] WHITE J A, BIRD D M. Implementation of gradientcorrected exchange-correlation potentials in Car-Parrinello total energy calculations [J]. Physical Review B, 1994, 50(21): 4954-4957.

[23] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Physical Review B, 1990, 41(11): 7892-7895.

[24] GARCIA A, ELSASSER C, ZHU J. Use of gradient-corrected functionals in total energy calculations for solids [J]. Physical Review B, 1992, 46(14): 9829-9832.

[25] ROSSO K M, RUSTAD J R, BYLASKA E J. The Cs/K exchange in muscovite interlayers: An ab initio treatment [J]. Clays and Clay Minerals, 2001, 49(6): 500-513.

[26] BICKMORE B R, ROSSO K M, NAGY K L. Ab intio determination of edge surface structures for dioctahedral 2:1 phyllosilicates: Implications for acid-base reactivity [J]. Clays and Clay Minerals, 2003, 51(4): 359-371.

[27] FRISH M J, TRUCKS G W, SCHLEGEL H B. Gaussian 03, G03RevB.01 [M]. Pennsylvania: Gaussian Inc, 2003.

[28] NEDER R B, BURGHAMMER M, GRASL T. Refinement of the kaolinite structure from single-crystal synchrotron data [J]. Clays and Clay Minerals, 1999, 47(4): 487-494.

[29] HU Yue-hua, LIU Xiao-wen, XU Zheng-he. Role of crystal structure in flotation separation of diaspore from kaolinite, pyrophyllite and illite [J]. Minerals Engineering, 2003, 16(3): 219-227.

[30] NWEMAN A C D. Chemistry of clays and clay minerals [R]. London: Longman Group UK Limited, 1987.

[31] XU Z H, PITT V, LIU Q. Recent advances in reverse flotation of diasporic ores—A Chinese experience [J]. Minerals Engineering, 2004, 17(9/10): 1007-1015.

[32] LEE L T, SOMASUNDARN P. Adsorption of polyacrylamide on oxide minerals [J]. Langmuir, 1989, 5(3): 854-860.

[33] ZHAO Shi-min, WANG Dian-zuo, HU Yue-hua. The flotation behavior of N-(3-aminopropyl)-dodecanamide on three aluminosilicates [J]. Minerals Engineering, 2003, 16(12): 1391-1395.

[34] MPOFU P, MENSAH J A, RALSTON J. Investigation of the effect of polymer structure type on flocculation, rheology and dewatering behaviour of kaolinite dispersions [J]. International Journal of Mineral Processing, 2003, 71(1): 247-268.

[35] JIANG Hao, HU Yue-hua, QIN Wen-qing, WANG Yu-hua, WANG Dian-zuo. Mechanism of flotation for diaspore and aluminum-silicate minerals with alkylamine collectors [J]. Chinese Journal of Nonferrous Metals, 2001, 11(4): 688-692. (in Chinese)

Foundation item: Project(2005CB623701) supported by the Major State Basic Research and Development Program of China; Project(50874118) supported by the National Nature Science Foundation of China; Project(2007B52) supported by the Foundation for the Author of National Excellent Doctoral Dissertation of China

Received date: 2008-04-01; Accepted date: 2008-08-26

Corresponding author: ZHONG Hong, Professor, PhD; Tel: +86-731-8830306; E-mail: zhongh@mail.csu.edu.cn

(Edited by CHEN Wei-ping)