J. Cent. South Univ. (2016) 23: 2118-2128

DOI: 10.1007/s11771-016-3268-9

Endpoint forecasting on composite regeneration by coupling cerium-based additive and microwave for diesel particulate filter

E Jia-qiang(鄂加强)^{1, 2}, ZUO Qing-song(左青松)^{1, 3}, LIU Hai-li(刘海力)¹, LI Yu(李煜)¹, GONG Jin-ke(龚金科)^{1, 2}

1. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China;

2. Institute of New Energy and Energy-saving & Emission-reduction Technology,

Hunan University, Changsha 410082, China

3. College of Mechanical Engineering, Xiangtan University, Xiangtan 411105, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2016

Abstract: Numerical simulation has been carried out to investigate the major factors affecting the time of composite regeneration due to coupling cerium-based additive and microwave for diesel particulate f3ilter (DPF). Effect on the composite regeneration time from various factors such as mass flow rate of exhaust gas, temperature of exhaust gas, oxygen concentration of exhaust gas, microwave power and amount of cerium-based additive are investigated. And a mathematical model based on fuzzy least squares support vector machines has been developed to forecast the endpoint of the composite regeneration. The results show that the relative error of endpoint forecasting model of composite regeneration is less than 3.5%, and the oxygen concentration of exhaust gas has the biggest effect on the endpoint of composite regeneration, followed by the mass flow rate of exhaust gas, the microwave power, the temperature of exhaust gas and the amount of cerium-based additive.

Key words: fuzzy least squares support vector machines; diesel particulate filter; composite regeneration; endpoint forecasting

1 Introduction

For a long time, single regeneration methods such as catalytic regeneration [1-2], continuous regeneration [3-4] and heating regeneration [5-6] have been the dominant methods employed for diesel particulate filter in vehicle [7-9]. However, one of the major challenges faced by single regeneration processes is that it cannot achieve continuous and effective regeneration of diesel particulate filter (DPF) [10-12]. The combination of microwave regeneration and proper cerium-based additive regeneration [13-14] can not only lowers the ignition temperature of the particles quickly, but also improves the utilization of microwave energy and reduces energy consumption, which is significantly better than the single regeneration or other composite regeneration processes. Composite regeneration process of DPF involves nonlinear coupling of high temperature and multiphase physical and chemical changes and the characteristics of multi- variable, nonlinear, strong coupling, large delay etc are obvious [14]. The fuzzy least squares support vector machine (FLS-SVM) has the advantages such as global optimal and high generalization ability and is superior in dealing with above problems [15-19]. Therefore, the fuzzy least squares support vector machines is adopted for endpoint forecasting on composite regeneration for Diesel Particulate Filter.

2 Mathematical model of composite regeneration process of DPF

The mathematical model on the composite regeneration process of DPF in vehicle is established based on the following assumptions:

1) The particles are made of pure carbon;

2) Particle deposition is ignored during the regeneration;

3) The influence on wall thickness and channel size of the filter body from the particle deposition layer is ignored;

4) The gas is an ideal gas, the specific heat capacity is a constant and Lewis number is 1;

5) The gas in the channel of filter body is laminar;

6) The heat generated by viscous dissipation is not considered;

7) The temperature of the filter body wall is equal to that of the particles, for the relative contact thermal resistance between the filter body and the particles is small;

8) The heat exchange between the filter body and the surrounding environment is ignored, that is, the boundary is adiabatic;

9) Fuel additives can only change the activation energy of the carbon particles.

2.1 Control equations

1) Conservation equation of gas phase mass

According to the law of mass conservation, the gas flowing into the control volume is equal to that flowing out of the control volume per unit time, and then conservation equation of gas phase mass is expressed as

                                         (1)

where ρ_j and u_j are the gas density and flow velocity, respectively, in the inlet or exhaust channels (j=1, means the inlet channel, and the plus sign is taken in the formula; j=2 means the exhaust channel, and the minus sign is taken in the formula; the same as below); ρ_w and u_w are the gas density and flow velocity, respectively, inside the filtering wall; a_c is the width of the channel.

Exhaust gas also satisfies the state equation of ideal gas as

                                   (2)

where p₀ is the atmospheric pressure, p₀=1.013×10⁵ Pa; M_g is the gas molar mass, M_g=0.029 kg/mol; R₀ is the gas constant, i.e., 8.314 J/(mol·K).

2) Conservation equation of gas phase momentum

Conservation equation of gas phase momentum is expressed as

                              (3)

where f is the friction coefficient; μ_j and p_j are the gas flow viscosity and pressure at the inlet or exhaust channels, respectively.

3) Conservation equation of gas phase energy

Conservation equation of gas phase energy is expressed as

            (4)

where c_g is the gas specific heat capacity, and c_g=1090 J/(kg·K); T_j is the gas temperature in the intake or exhaust channels, when j=1, the minus sign is taken in the formula; when j=2, the plus sign is taken instead; T_w is the gas temperature inside the filter wall; h_j is the convective heat transfer coefficient in the intake or exhaust channels.

4) Balance equation of oxygen concentration

The oxygen concentration inside the deposition layer of the carbon particles is expressed as

          (5)

where O_soot is the oxygen concentration inside the particle deposition layer; O_w is the oxygen concentration inside the filtering wall; S_p is the specific surface area of the particles, S_p=5.5×10^{-7 m-1}; k_O is the pre-exponential factor of the reaction rate, with the value of 596 m/(s·K); E is the activation energy of the reaction.

The oxygen concentration inside the filter wall is expressed as

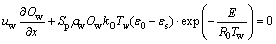   (6)

where ε_s is the porosity of the filter wall surface at any time; ε₀ is the porosity of the filter wall surface of a clean filter body.

5) Conservation equations of particle phase mass

The mass conservation equation inside the particle deposition layer is expressed by

           (7)

where O_f is the oxygen concentration at the inlet; ρ_pw is the bulk density of the particle deposition layer, and its value is set to 127 kg/m³; w_s is the thickness of the filter wall; M_C and M_O are the molar mass of carbon and oxygen, with the values of 0.012 kg/mol and 0.032 kg/mol, respectively.

The mass conservation equation inside the filter wall is expressed by

                   (8)

where ρ_pws is the bulk density of the particles inside the filtering wall, ρ_pws=14 kg/m³; β is the complete coefficient of particles oxidation reaction, β = 0.75.

6) Microwave energy equation

According to the law of energy conservation, the amount of the microwave energy absorbed by the control volume is equal to the net inflow of the microwave energy per unit time, the amount of the reflection microwave energy absorbed by the body is equal to the net inflow of the reflective microwave energy per unit time, and then,

                                           (9)

                                                 (10)

where P_mi and P_mo are the energy stream surface densities of the incident and reflective waves, respectively; Γ is the reflection coefficient of the filter body wall; α_eff is the equivalent attenuation constant of wall-flow type filter body.

7) Conservation equation of particle energy

Conservation equation of the particle energy is expressed by

               (11)

where H_ac is the heat gathered in the control body per unit time; H_conin is convective heat transfer into the control body in the intake channels; H_conout is convective heat transfer into the control body in the exhaust channels; H_cond is the net conduction heat into the control body; H_rl is the heat released by the oxidation combustion of the particles absorbed by the control body; H_m is the microwave radiation heat absorbed by the body.

The heat conduction coefficients of the particles and filter wall are λ_soot and λ_s respectively, with the values of 0.84 W/(m·K) and 1.1 W/(m·K). The specific heat capacities of the particles and the filter wall are C_p and C_s, with the value of 1510 J/(kg·K) and 1110 J/(kg·K); the density of the filter wall is ρ_s, with a value of 1300 kg/m³.

2.2 Oxidation model of particles

The combustion process of the carbon particles is an exothermic reaction, and enthalpy △H of formation is related to the complete coefficient β of the particulate oxidation reaction:

                     (12)

where △H₁ is the formation enthalpy of CO₂, with a value of -3.61×10⁵ J/mol; △H₂ is the formation enthalpy of CO, with a value of -0.9×10⁵ J/mol.

According to Arrhenius law, the rate of oxidation reaction of the particles is expressed as

                                    (13)

where A is the pre-exponential factor of the reaction rate, with a value of 596 m/(s·K); E is the activation energy of the reaction with a value of 150 kJ/mol, without catalytic action.

2.3 Initial and boundary conditions

At the initial time of the composite regeneration of DPF, the thickness of the soot particulate layer and the porosity of the surface in the filter wall are known, the temperature of the filter wall is equal to that of the gas inside the intake and exhaust channels, therefore, the initial conditions are:

T_in(t=0, z)=T_out(t=0, z)=T_w(t=0, z)=T_b                        (14)

where T_b is the initial temperature of the filter wall.

w_soot(t=0, z)=w_b                                                                                  (15)

where w_b is the initial thickness of the soot particulate layer.

ε_s(t=0, z)=ε_{s_0}                                                    (16)

where ε_{s_0} is the initial porosity of the filter wall.

At the entrance of the intake channel of exhaust gas, the temperature T_in of the exhaust gas is equal to the temperature T_f of upstream exhaust gas, the content O_in of the oxygen in exhaust gas is equal to the content O_f of the upstream oxygen in exhaust gas, the mass flow rate ρ_inu_in of exhaust gas is equal to the mass flow rate ρ_fu_f of upstream exhaust gas. Therefore,

T_in(t>0, z=0)=T_f(t>0)                                   (17)

O_in(t>0, z=0)=O_f(t>0)                                  (18)

ρ_in(t>0, z=0)u_in(t>0, z=0)=ρ_fu_f (t>0)                        (19)

At the outlet channel of the exhaust gas, its pressure is equal to the atmospheric pressure since it is open to the outside atmosphere. Therefore,

p_out(t>0, z=L)=p_atm(t>0)                                   (20)

At the front surface of the filter body, the energy of the incident microwave is the energy emitted by the microwave source, the reflection coefficient of the front surface is known as follows:

P⁺_mw(t>0, z=0)=P_{mw_0}(t>0)                                          (21)

Г_mw(t>0, z=0)=Г₀(t>0)                                   (22)

where P_{mw_0}(t>0) is the energy density emitted by the microwave source.

There is no flow at the front end of the outlet channel and the rear end of the inlet channel, therefore, the mass flow of exhaust gas is 0 at these two positions:

ρ_in(t>0, z=0)u_in(t>0, z=0)=0                      (23)

ρ_out(t>0, z=L)u_in(t>0, z=L)=0                    (24)

According to the hypothesis (h), the front surface and rear end surface of the filtering wall is adiabatic, and then changes in temperature gradient conditions in the cases are calculated as following:

                              (25)

                                        (26)

In addition, in order to solve the energy equation (Eq. (4)) inside the outlet channel in the composite regeneration process of the vehicle particulate filter, it can be assumed as

T_out(t>0, z=0)=T_w(t>0)                         (27)

2.4 Effect of various operating conditions on composite regeneration time

The space domain is set to x=0-L, the time domain is set to t=0-t_max, t_max is the maximum of the calculation time, the space step and the time step are △z and △t, respectively. L is the length of the channel.

Calculation is based on the standard pressure solver SIMPLE algorithm and equations of momentum and species are set as second order upwind difference scheme.

2.4.1 Effect of mass flow rate x₁ of exhaust gas on composite regeneration time

When the mass flow rate x₁ of exhaust gas is within the range of 40-80 kg/h, the composite regeneration time is quite stable. With the increase of the mass flow rate x₁ of exhaust gas from 80 kg/h to160 kg/h, the composite regeneration time increases quickly. As shown in Fig. 1, when the mass flow rate x₁ of exhaust gas is more than 145 kg/h, the growth trend of the composite regeneration time will slow down.

Fig. 1 Effect of mass flow x₁ of exhaust gas on composite regeneration time y

Obviously, when the exhaust gas flows through the particulate filter, the carbon particles in the particulate filter will be cooled by the exhaust gas so that combustion of the carbon particle slows down. With increase of the mass flow rate x₁ of exhaust gas, more heat will be taken away per unit time, the cooling effect will be more obvious and the speed of combustion of the carbon particles will be further reduced. Therefore, the composite regeneration time y presents an increasing tendency with the increase of the mass flow x₁ of the exhaust gas.

In another words, smaller mass flow rate x₁ of exhaust gas is more favorable to shorten the composite regeneration time y.

2.4.2 Effect of temperature x₂ of exhaust gas on composite regeneration time

As shown in Fig. 2, the composite regeneration time y gradually decreases with the increase of the temperature temperature x₂ of exhaust gas, which has an approximately linear relation. Obviously, with the increase of the temperature x₂ of exhaust gas, the preheating time of the carbon particles is shortened and the cooling effect is also reduced. As a result, the composite regeneration time y presents a decreasing trend with the increase of the temperature x₂ of exhaust gas.

Fig. 2 Effect of temperature x₂ of exhaust gas on composite regeneration time y

2.4.3 Effect of oxygen concentration x₃ of exhaust gas on composite regeneration time

As shown in Fig. 3, the composite regeneration time y decreases with the increase of the oxygen concentration x₃ of exhaust gas. When the oxygen concentration x₃ of exhaust gas is less than 7%, it is very obvious that the composite regeneration time decreases rapidly with increase of the oxygen concentration x₃ of exhaust gas. When the oxygen concentration x₃ of exhaust gas is higher than 7%, the decreasing tendency of the composite regeneration time gradually slows down with the increase of the oxygen concentration x₃ of exhaust gas.

The following explanations are useful to explain the above phenomena. It is obvious that the carbon particles are oxidized slowly at the low oxygen concentration x₃ of exhaust gas, therefore, the composite regeneration time y becomes longer. With the increase of the oxygen concentration x₃ of exhaust gas, the oxidation rate of the carbon particles speeds up. Some carbon particles begin to burn when the oxygen concentration x₃ of exhaust gas exceeds a certain value and the speed of combustion accelerates with a further increase of the oxygen concentration x₃ of exhaust gas until the majority of carbon particles start burning, at this point the reaction rate of the carbon particles has reached a higher level, i.e., the composite regeneration time y has reached a relatively low value. As the oxygen concentration x₃ of exhaust gas exceeds a certain value, the decrease amplitude of the composite regeneration time y starts decreasing.

Fig. 3 Effect of oxygen concentration x₃ of exhaust gas on composite regeneration time y

From the viewpoint of the composite regeneration time y, the oxygen concentration x₃ of exhaust gas need not be too high, it is appropriate to be maintained within range of from 10% to 15%.

2.4.4 Effect of microwave power x₄ on composite regeneration time

As shown in Fig. 4, the composite regeneration time y decreases gradually with the increase of the microwave power x₄. Due to effect of the combustion rate of the carbon particles, the composite regeneration time y reduces rapidly when the microwave power x₄ changes from 0.5 kW to 0.65 kW and the decreasing trend of the composite regeneration time y slows down gradually when the microwave power x₄ further increases to 1.0 kW.

Fig. 4 Effect of microwave power x₄ on composite regeneration time y

Based on the results, it seems that the preferred microwave power is within the range of 0.7-1.0 kW.

2.4.5 Impact of amount x₅ of cerium-based additive on composite regeneration time

Figure 5 presents the impact of the amount x₅ of cerium-based additive on the composite regeneration time.

Fig. 5 Effect of amount of cerium-based additive x₅ on composite regeneration time y

As shown in the Fig. 5, when the microwave power is set to be 0.75 kW or 0.85 kW, the composite regeneration times decrease linearly with the increase of the amount x₅ of cerium-based additive. Because the activation energy of the carbon particles will decrease with the increase of the amount x₅ of cerium-based additive and the carbon particles are more prone to be oxidized, which will result in reduced pre-heating time of the carbon particles, the increase of combustion rate and decrease of the composite regeneration time y.

The amount x₅ of cerium-based additive has a greater impact on the decrease of the composite regeneration time y, so the cerium-based additives can be selected to reduce the activation energy of the carbon particles for shortening the composite regeneration time y.

3 Endpoint forecasting model on composite regeneration for diesel particulate filter based on fuzzy least squares support vector machine

It can be seen from above simulation results that several parameters such as the temperature of exhaust gas, mass flow rate of exhaust gas, and oxygen concentration of exhaust gas have an important effect on the composite regeneration time of diesel particulate filter. In addition, the microwave power and activation energy of the carbon particles also have an impact on the composite regeneration process. Therefore, the above 5 parameters are selected as the characteristic parameters of the composite regeneration of diesel particulate filter.

Based on the fuzzy least squares support vector machine (SVM), the input fuzzy sample of the endpoint forecasting on composite regeneration due to coupling cerium-based additive and microwave for diesel particulate filter is expressed as follows:

(x₁, y₁, μ(x₁)), (x₂, y₂, μ(x₂)), …, (x_k, y_k, μ(x_k)); k=1, 2, …, 5

where μ(x_k) is the membership, 0<μ(x_k)≤1.

Through the fuzzy membership μ(x_k) of the characteristic parameters for the endpoint of composite regeneration, the optimal classification surface of the fuzzy least squares support vector machine is the optimal solution of the objective function in Eq. (28).

  (28)

where C is the regularization parameter; b is the threshold, ε_k is relaxation variable.

The corresponding Lagrangian function is expressed by

k=1, …, 5   (29)

The optimization problem of fuzzy least squares support vector machine (SVM) is transformed into solving linear equations:

                     (30)

where y=[y₁, y₂, y₃, y₄, y₅]^T; E=[1, 1, 1, 1, 1]^T; a=[a₁, a₂, a₃, a₄, a₅]^T; Ω_kl=φ(x_k)·φ(x_l)=K(x_k, x_l), l=1, …, 5.

So, the endpoint forecasting model of composite regeneration due to coupling cerium-based additive and microwave for diesel particulate filter is expressed by the formula (31).

                                         (31)

where x=[x₁, x₂, x₃, x₄, x₅]; ; σ is the kernel parameter.

The endpoint forecasting network of composite regeneration due to coupling cerium-based additive and microwave for diesel particulate filter is shown in Fig. 6, the selection of the regularization parameter C and the kernel parameter σ is very important when the fuzzy least squares support vector machine is applied in this kind of problem.

Fig. 6 Endpoint forecasting network of composite regeneration due to coupling cerium-based additive and microwave for diesel particulate filter

3.1 Determination of fuzzy membership

The input samples of the endpoint forecasting on composite regeneration include the parameters such as the temperature of the exhaust gas, the mass flow of the exhaust gas, the oxygen concentration of the exhaust gas, the microwave power and the amount of cerium-based additive and the output samples of the endpoint forecasting on composite regeneration include the composite regeneration time. It is obvious for the input samples and the output samples that their variable dimensions, the distribution of data, the mean value of data and variance are different, the following methods can be used to determine the fuzzy membership of the parameters data in order to decrease bad effects from the input samples and the output samples.

Set X_kj as the original data of the jth sample data of the kth variable, X_kjmax, X_kjmin the maximum and minimum data in the jth sample data of the kth variable respectively, then the fuzzy membership x_kj of the jth sample data of the kth variable can be expressed by

                                       (32)

3.2 Optimization on parameters of least squares support vector machine by adaptive variable-scale chaos genetic algorithm

The regularization parameter C and kernel parameter σ are the key parameters of the least squares support vector machine which requires to be optimized by adaptive variable-scale chaos genetic algorithm. It is very key how to determine the fitness function in the adaptive variable-scale chaos genetic algorithm [20-21]. Therefore, the fitness function is selected by

                            (33)

where y_j is the expect output; f(x_kj) is the actual output; j=1, …, n; e is a very small real number, in order to prevent the denominator being zero, set e=10^{-5 in the paper.}

And the error function MSE is defined as an evaluation index [22-23] of the generalization performance of the least squares support vector machine:

                                   (34)

3.3 Simulation analysis of endpoint forecasting on composite regeneration for diesel particulate filter

As listed in Table 1, the values including the mass flow x₁ of the exhaust gas, the temperature x₂ of the exhaust gas, oxygen concentration x₃ of the exhaust gas, microwave power x₄ and the amount x₅ of cerium-based additive and the composite regeneration time y of the diesel particulate filter can be obtained after 200 times simulation experiments being done.

Table 1 Simulation results of endpoint forecasting on composite regeneration based on characteristic parameters

After the memberships of the characteristic parameters and the composite regeneration time based on the simulation results due to coupling cerium-based additive and microwave for diesel particulate filter is determined, the membership μ(y) of the composite regeneration time is taken as the output of the fuzzy support vector machine and the membership μ(x₁) of the mass flow x₁ of the exhaust gas, the membership μ(x₂) of the temperature x₂ of the exhaust gas, the membership μ(x₃) of oxygen concentration x₃ of the exhaust gas, the membership μ(x₄) of microwave power x₄ and the membership μ(x₅) of the amount x₅ of cerium-based additive are treated as the input of the fuzzy support vector machine. The target values of the error function MSE “S” are set at 10^-4 and 10^-5, then lgS=lg(10^-4)=-4 or lgS=ln(10^-5)=-5, the maximum number of training is 550. The relationship between the training steps and the training errors of the endpoint forecasting model on composite regeneration for vehicle particulate filter based on the fuzzy least squares support vector machine is shown in Fig. 7. It can be observed from the figure that the average error “S” of the endpoint forecasting model on composite regeneration for vehicle particulate filter converges to 10^-4 or 10^-5 after 174 steps or 389 steps of training, respectively.

The comparison of the relative errors of the endpoint forecasting model in the paper with those of the methods from Ref. [15] or those of Ref. [16] are shown in Fig. 8.

It can be seen from Fig. 8 that the maximum errors of the method in Ref. [15] or the method in Ref. [16] arerespectively 2.44% 2.14% and, while the maximum error of the endpoint forecasting model in the paper is less than 0.76%. Obviously, the endpoint forecasting on composite regeneration for diesel particulate filter based on the fuzzy least squares support vector machine is of higher forecasting precision than the method in Ref. [15] or the method in Ref. [16].

Fig. 7 Relationship between training steps and training errors

Fig. 8 Relative errors between forecasting values and actual values of composite regeneration endpoint for diesel particulate filter

The partial derivative a_i of the fuzzy least squares support vector machine is used to evaluate the influence of the mass flow x₁ of the exhaust gas, the temperature x₂ of the exhaust gas, oxygen concentration x₃ of the exhaust gas, microwave power x₄ and the amount x₅ of cerium-based additive on composite regeneration. A bigger value of the partial derivative a_i means a greater influence. The influence of every index parameter on endpoint forecasting of composite regeneration are shown in Fig. 9. The results indicate that a₃>a₁>a₄>a₂>a₅, i.e. the oxygen concentration x₃ of exhaust gas is of the greatest influence, followed by the mass flow x₁ of exhaust gas, the microwave power x₄, the temperature x₂ of exhaust gas and the amount x₅ of cerium-based additive.

Fig. 9 Weight coefficients of capability index parameters about composite regeneration endpoint for diesel particulate filter in vehicle

3.4 Experimental verification

The device for experimental verification of the endpoint forecasting on composite regeneration for diesel particulate filter based on the fuzzy least squares support vector machine is shown in Fig.10. In order to ensure the accuracy of the experiment, asbestos is used to minimize the heat loss from the hot-gas pipelines, the heat exchanger and the diesel particulate filter.

The diesel engine is YC6M320 with a EX-80 cordierite wall-flow filter. 0# diesel is used as fuel. 2M236 magnetron produced by the Panasonic (the output power is 900 W, frequency is (2455±30) MHz) is used to produce microwave. Four working conditions are designed and tested as listed in Table 2.

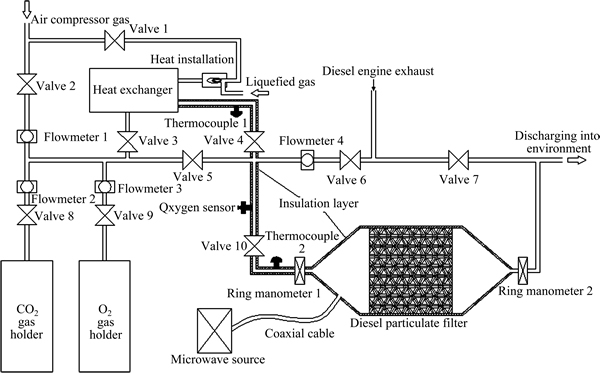
Fig. 10 Schematic of experimental setup

Table 2 Experimental working conditions

The specific experimental procedure:

Step 1: Shut off valve 6, 7, 4, 3, 8 and 2, open valve 5, 9 and 10 in no working case of the magnetron and the air compressor, let O₂ from the gasholder flow through the clean diesel particulate filter and record the pressure drop through the diesel particulate filter △p₁. To make sure the accuracy, the average value △p_1m from 10 groups of data is recorded.

Step 2: Stablize the working condition: let the diesel engine be operated at the speed of 1500 r/min and load of 50%, shut off valve 4, 5 and 7 and open valve 6 and 10 in order that the exhaust gas flows through the diesel particulate filter, keep carbon particles be captured for 3 hours and then stop the diesel engine.

Step 3: Control CO₂, O₂ and flow rate of the air by using of valve 2, 8, 9 and the flowmeter 1, 2, 3, so as to adjust the gas components during the composite regeneration process by using of shutting off valve 1, 3, 4, 10 and opening valve 5.

Step 4: Shut off valve 5 and open valve 3 after the adjustment, so that the gas can be heated by the heat exchanger. Thermocouple 1 shows the temperature of the gas from the heat exchanger and the gas will be discharged into the atmosphere directly through valve 6 and 7 if its temperature does not meet the experimental requirements. Shut off valve 6 and open valve 10 and 4 when the experimental requirements have been met, let the gas flow into the diesel particulate filter, switch on the microwave source and carry out the experiment of composite regeneration for diesel particulate filter according to the working condition 1.

Step 5: Record the amount of cerium-based additive added into the diesel fuel, and collect the readings of the magnetron power, the mass rate at flowmeter 4, oxygen concentration, temperature at thermocouple 2 and mass flow rates at annular flowmeter 1, 2, etc. It can be treated as endpoint of the composite regeneration process for diesel particulate filter when the pressure drops at the annular flowmeter 1 and 2 are equal, △p_1m=△p₂(when the relative errors between △p_1m and △p₂ are less than 3%), then record the composite regeneration time τ₂.

Step 6: Repeat Step 2-Step 5 under the working condition 2, 3 and 4, collect four groups of data including the pressure drops △p₂ at the annular flowmeter 1 and 2, and the composite regeneration time τ₂, and then compare them with the endpoint forecasting value τ₁ as shown in Table 3.

It can be observed from Table 3 that the relative errors between the pressure drop of the diesel particulate filter and that of the clean particulate filter under working conditions 1-4 are respectively 2.1277%, 2.9126%, 1.4925% and 1.2903% on the endpoint of the composite regeneration. The corresponding errors between the endpoint forecasting values are -0.7246%, -3.4188%, -2.4793% and -1.7544%, respectively. Obviously, the endpoint forecasting model of composite regeneration for diesel particulate filter based on the fuzzy least squares support vector machine is of good forecasting precision.

Table 3 Comparison between experimental value and predicted value

4 Conclusions

Numerical simulation has been carried out to investigate the major factors affecting the composite regeneration time due to coupling cerium-based additive and microwave for diesel particulate filter. The results indicate that the composite regeneration time is significantly affected by the mass flow rate of exhaust gas, the temperature of exhaust gas, the oxygen concentration of exhaust gas, the microwave power and the amount of cerium-based additive. A mathematical model based on fuzzy least squares support vector machines has also been developed to forecast the endpoint of the composite regeneration, which is validated by experimental test. The results show that the relative error for endpoint forecasting on composite regeneration is less than 3.5%, and the oxygen concentration of exhaust gas has the biggest effect on the endpoint of the composite regeneration, followed by the exhaust mass flow rate, the microwave power, the exhaust temperature and the amount of cerium-based additive.

References

[1] FINO D, FINO P, SARACCO G, SPECCHIA V. Innovative means for the catalytic regeneration of particulate traps for diesel exhaust cleaning [J]. Chemical Engineering Science, 2003, 58(3/4/5/6): 951- 958.

[2] CAUDA E, FINO D, SARACCO G, SPECCHIA V. Preparation and regeneration of a catalytic diesel particulate filter [J]. Chemical Engineering Science, 2007, 62(18/19/20): 5182-5185.

[3] TANG Tao, ZHANG Jun, CAO Dong-xiao, SHUAI Shi-jin, ZHAO Yan-guang. Experimental study on filtration and continuous regeneration of a particulate filter system for heavy-duty diesel engines [J]. Journal of Environmental Sciences, 2014, 26(12): 2434-2439.

[4] LIU Zhi-hua, GE Yun-shan, TAN Jian-wei, HE Chao, SHAH A N, DING Yan, YU Lin-xiao, ZHAO Wei. Impacts of continuously regenerating trap and particle oxidation catalyst on the NO₂ and particulate matter emissions emitted from diesel engine [J]. Journal of Environmental Science, 2012, 24(4): 624-631.

[5] ZHENG Ming-gang, GAO Hui, ZHU Xiao-hui. Research on developing DPF blowback heating regeneration device [J]. Procedia Engineering, 2011, 16: 661-666.

[6] CHEN K, MARTIROSYAN K S, LUSS D. Temperature gradients within a soot layer during DPF regeneration [J]. Chemical Engineering Science, 2011, 66(13): 2968-2973.

[7] BOGDANIC M, BEHRENDT F, MERTINS F. The influence of a 2-component model on the computed regeneration behavior of an uncoated diesel particulate filter [J]. Chemical Engineering Science, 2008, 63: 2601-2613.

[8] LIU Yun-qing, GONG Jin-ke, FU Jun, CAI Hao, LONG Gang. Nanoparticle motion trajectories and deposition in an inlet channel of wall-flow diesel particulate filter [J]. Journal of Aerosol Science, 2009, 40(4): 307-323.

[9] BOSE P K, ROY K, MUKHOPADHYAY N, CHAKRABORTY R K. Improved theoretical modeling of a cyclone separator as a diesel soot particulate emission arrester [J]. International Journal of automotive technology, 2010, 11(1): 1-10.

[10] A. Preparation, characterisation and testing of CuO/Ce0.8Zr0.2O₂ catalysts for NO oxidation to NO₂ and mild temperature diesel soot combustion [J]. Applied Catalysis B: Environmental, 2014, 152/153: 99-107.

[11] BENJAMIN S F, ROBERTS C A. Three-dimensional modelling of NO_x and particulate traps using CFD: A porous medium approach [J]. Applied Mathematical Modelling, 2007, 31: 2446-2460.

[12] KOSTOGLOU M, KONSTANDOPOULOS A. Effect of soot layer microstructure on diesel particulate filter regeneration [J]. Aiche Journal, 2005, 51: 2534-2546.

[13] ZUO Qing-song, E Jia-qiang, GONG Jin-ke, WANG Shu-hui, WANG Chao, CHEN Tao, GAO Jun-xu. Analysis and evaluation of active based on MnOx-CeO₂ catalysts in process of particle combustion for diesel particulate filter [J]. Applied Mechanics and Materials, 2012, 217/218/219: 796-800.

[14] ZUO Qing-song, E Jia-qiang, ZHANG D M, CHEN Tao, JIA Guo-hai. Performance evaluation on field synergy and composite regeneration by coupling cerium-based additive and microwave for a diesel particulate filter [J]. Journal of Central South University, 2014, 21(12): 4599-4606.

[15] JIANG Xiu-feng, YI Zhang, L Jian-cheng. Fuzzy SVM with a new fuzzy membership function [J]. Neural Computing and Application, 2006, 15: 268-276.

[16] LIN C F, WANG S D. Fuzzy support vector machines [J]. IEEE Transactions on Neural Networks, 2002, 13(2): 464-471.

[17] WANG Tao-sheng, ZUO Hong-yan. Fuzzy least squares support vector machines soft measurement model based on adaptive mutative scale chaos immune algorithm [J]. Journal of Central South University, 2014, 21(2): 593-599.

[18] ZUO Hong-yan, LUO Zhou-quan, GUAN Jia-lin, WANG Yi-wei. Identification on rock and soil parameters for vibration drilling rock in the metal mine based on the fuzzy least square support vector machine [J]. Journal of Central South University, 2014, 21(3): 1085-1090.

[19] ZUO Hong-yan, LUO Zhou-quan, WU Chao. Classification identification on acoustic emission signals from underground metal mine rock by ICIMF classifier [J]. Mathematical Problems in Engineering, 2014, 2014: 1-9.

[20] WANG He-jun, E Jia-qiang, DENG Fei-qi. A novel adaptive mutative scale optimization algorithm based on chaos genetic method and its optimization efficiency evaluation [J]. Journal of Central South University of Technology, 2012, 19(9): 2554-2560.

[21] E Jia-qiang, WANG Chun-hua, WANG Yao-nan, GONG Jin-ke. A new adaptive mutative scale chaos optimization algorithm and its application [J]. Journal of Control Theory & Applications, 2008, 6(2): 141-145.

[22] E Jia-qiang. Intelligent fault diagnosis and its application [M]. Changsha: Hunan University Press, 2006. (in Chinese)

[23] WANG Chun-hua, ZHONG Zhao-ping, LI Rui, E Jia-qiang. Prediction of jet penetration depth based on least square support vector machine [J]. Powder Technology, 2010, 203: 404-411.

(Edited by DENG Lü-xiang)

Foundation item: Projects(51176045, 51276056) supported by the National Natural Science Foundation of China; Project(201208430262) supported by the National Studying Abroad Foundation Project of China

Received date: 2015-04-14; Accepted date: 2015-09-14

Corresponding author: ZUO Qing-song, PhD; Tel: +86-18274782195; E-mail: zuo-qingsong@163.com