Trans. Nonferrous Met. Soc. China 31(2021) 1175-1188

Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions

Xiao-lin TIAN, Yu-hong ZHAO, Dun-wei PENG, Qing-wei GUO, Zhen GUO, Hua HOU

School of Materials Science and Engineering, North University of China, Taiyuan 030051, China

Received 10 April 2020; accepted 28 February 2021

Abstract: Pre-melting is a phenomenon that below the melting point the liquid-like structure appears at the grain- boundary while the grain interior remains a crystal structure. The phase-field crystal method was employed to investigate the early evolution of the liquid pools in pre-melting regions, mainly involving four structural transformations: solid-solid state→small droplet→large liquid pool→homogeneous liquid melting. The microscopic morphology and free energy variation with different average atomic densities demonstrate that the average atomic density is sensitive to the morphological characteristics of liquid pools. Both two-dimensional and three-dimensional simulation results show that the amplitude reduction of order parameters can promote the order-disorder transition of grain boundaries, causing pre-melting in the edge dislocation aggregation. The relationship between the average atomic density and the width of the liquid pools is verified from thermodynamics, which provides a prerequisite for the application of high-temperature strain in the later stage to some extent.

Key words: phase-field crystal method; pre-melting; edge dislocations; liquid pools

1 Introduction

The special properties of metal materials in the nano-scale tremendously depend on the internal microstructure [1,2]. Therefore, scholars are required to constantly go deep into the micro-nano level to investigate the internal structure and defects of materials [3,4]. As a kind of surface defect, grain boundary is characterized by a loose structure formed by the irregular arrangement of atoms. These structures are not fixed and they can change accordingly at different temperatures [5]. Most of the grain boundaries (GBs) remain in equilibrium at low temperatures. However, the GBs change from an ordered state to a disordered state as temperature increases, particularly near the melting point. At the GBs, impurity atoms are enriched by the component segregation and internal adsorption, causing the decrease of melting point. Therefore, the sample is easy to induce pre-melting during the heating process [6,7]. This phenomenon was first observed in pure aluminum [8]. Subsequently, ALSAYED et al [6] found grain boundary pre-melting (GBPM) at the dislocation aggregation of the thermal reaction gel sphere. This type of GBPM was defined as defect-induced pre-melting. However, a weakness of this method is that it is sometimes difficult to accurately observe the specific process of GBPM [9-11]. Therefore, computer simulation exerts a prominent role as a bridge between macro-experiment and micro-theory.

ELDER et al [12,13] proposed the phase-field crystal (PFC) model based on the classical density functional theory, which laid the theoretical foundation of PFC. As a chain between the molecular dynamics (MD) [14-16] and the traditional phase-field method (TPF) [17-19], the proposed method can be self-consistently coupled from the time scale of atomic vibration characteristics (10^-12 s) to the thermal and mass diffusion time scale (10^-6 s) related to dislocation dynamics [20]. On this basis, the symmetry on the lattice level can be displayed to reflect the physical properties associated with certain periodicities, such as elastic-plastic deformation, dislocation defects, and elastic distortion of the lattice [21,22]. By employing a simple PFC model, MELLENTHIN  et al [23] reported the GBPM phenomenon of a two-dimensional (2-D) hexagonal phase when the temperature was below the melting point from a thermodynamic point. In the meantime, they also found the standard critical wetting conditions and the relationship between the separation potential of the giant canonical system and the liquid film width, providing a theoretical thermodynamic basis for GBPM research. ADLAND et al [24] quantitatively calculated the disjoining potential of the whole range of θ=0°-90° in (BCC) Fe. When θ_min<θ<θ_max, the width of liquid layer had logarithmic divergence, corresponding to a pure repulsive disjoining potential. Otherwise, it was an attractive disjoining potential.

In recent years, some scholars have been keen to study the characteristics of pre-melting or melting region structures of defects such as grain boundary dislocations under high-temperature stress, and have also achieved a lot of meaningful results [25-29]. However, these results were based on the existence of a stable pre-melted or melted structure in the early stage, which had a high dependence on the average atomic density [30-35]. Consequently, understanding the early evolution of the GBPM region and the influence of different atomic densities on its structure in the stress-less state would provide a prerequisite for strain application at the later stage.

In the present study, we systematically study the effect of average atomic density on the rule of the early evolution and transformation of liquid pools in the GBPM region characterized by atomic density distribution and free energy change. And the behavior for the atomic density dependence of the liquid pool width can qualitatively be calculated by the thermodynamic method.

2 PFC model of pre-melting

2.1 Model and basic equations

The phase-field crystal model (PFC) is closely related to the classical density functional theory (CDF) [36-38]. The unique feature of this model is that the free energy function is constructed into a conservative atomic density field system with periodically ordered parameters, which can better display the structural characteristics and atomic- scale behavior of the crystalline [39,40]. The PFC model was first derived from the Swift-Hohenberg equation of nonlinear dynamics [13,41,42]. It could show the periodic structure of crystal by one ground state of free energy. After the dimensionless treatment, free energy can be expressed as

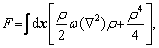
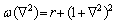  (1)

where F is the total free energy of the system as the function ρ. ρ is local-time-averaged atomic density, which is a periodic density wave in solid phase and a constant in liquid phase. 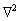stands for the Laplace operator. r is a parameter related to the temperature. The smaller the absolute value of r is, the higher the actual temperature is.  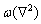indicates the state of the wave in the reciprocal space, reflecting the periodic structure of the  system. x is the spatial position vector.

In this model, the evolution of locally conserved order parameters is described by the Cahn-Hillard dynamic equation of the conservative field [14,43]:

               (2)

where t is the time step.

To minimize the free energy, the expression of Eq. (1) can be obtained by single-mode approximation [44]. After dimensionless treatment, atomic density for the triangular phase in equilibrium can be approximated as

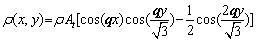    (3)

where q is the wave vector, A_t denotes the periodic structure amplitude of solid-state atomic density. The expression of amplitude A_t and wave vector q is obtained by substituting the above formula into the free energy function of Eq. (1), and the results are

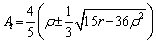                  (4)

According to Ref. [45], we can obtain the form of the minimum free energy function about the liquid phase, triangular phase, and strip phase. The two-dimensional (2-D) phase diagrams of the three phases can be determined by the calculation method of equilibrium phase diagrams, as shown in Fig. 1.

2.2 Numerical method

In this work, the semi-implicit Fourier spectral method [10,46] is used to solve Eq. (2) in time and space. One of the advantages of this method is that the Laplacian operator with high order can be expressed by the algebraic expression of the wave vector in frequency space. After transformation, this method is in line with the periodic lattice law of crystal arrangement. Therefore, the atomic density at the next moment can be simplified by discretizing Eq. (2) in space and time:

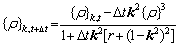              (5)

where k is the wave vector of Fourier space and satisfies k²=|k|². {ρ}_k,t and {ρ}_k,t+△t represent the atomic density at the time t and the next time t+△t in Fourier space, respectively.

2.3 Parameter setting and simulation details

2.3.1 Design of initial parameters

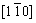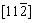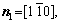
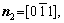
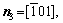
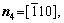
For simplicity, the crystalline symmetry of the triangular phase in 2-D is equivalent to the {111} family of planes in a face-centered cubic (fcc) lattice, as shown in Fig. 2. Assuming that the directions of the x-axis and the y-axis are  and , respectively, for the triangular phase, the six vector directions of the extra half-atom  array can be expressed as    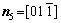and 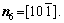 According to the Ref. [47], space step and time step are set as △x=△y=π/4 and △t=0.5, respectively. The scale range of the standard square is set as L_x×L_y=512△x×512△y. To set the bi-crystal structure, the simulation region is divided into three parts: 0x/4, L_x/4x/4, and 3L_x/4x.

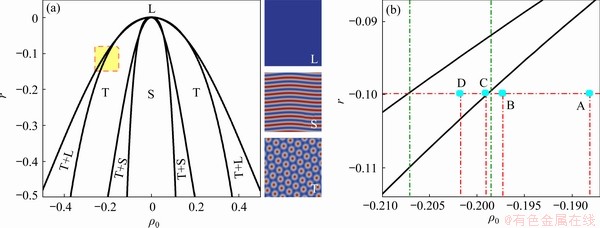
Fig. 1 Two-dimensional (2-D) phase diagram used in simulation (L, S and T represent liquid phase, strip phase, and triangular phase, respectively) (a) and partial enlargement drawing (b)

Fig. 2 Schematic diagrams of face-centered cube (fcc) structure

2.3.2 Simulation details

The simulation process in this work is divided into the following three stages, and the specific parameters involved are given in Table 1.

(1) Prepare solidified bi-crystal samples at low temperature (r=-0.3). The method is to make the initial liquid phase rapidly solidify through heterogeneous nucleation to form a stable grain boundary after solidification (i.e. the initial grain boundary of premelting in the following text);

(2) Load at a constant dimensionless strain rate (ε^·=2×10^-6) and heat the sample to a high temperature (r=-0.1) (below the melting point), so that the pre-melting of solid phase grain boundary formed in (1) occurs;

(3) Keep the temperature at (2) to make the sample more fully pre-melted to form a liquid-like region.

3 Simulation results

3.1 Microstructure of GBs

Figure 3 shows the atomic density evolution diagram during the initialization stage of the solid phase corresponding to Sample A (r=-0.3 and ρ₀=-0.198). The initial crystal nucleus with θ=8.4° is pre-set in the supercooled liquid phase, as shown in Fig. 3(a). It can be seen that there is a supercooled liquid phase between the two nuclei, which is shown in the dark blue region with uniform color. As the solidification process continues, the crystal nucleus in Fig. 3(b) continues to grow and consumes the surrounding liquid phase. At this time, the disordered atoms in the liquid phase are driven by free energy to move into the solid phase and occupy the corresponding balance position. When t* continues to extend, the supercooled liquid phase in the system is exhausted, and the grain boundary structure can be observed in the stable triangular phase in Fig. 3(c).

The microstructural morphology of the low-angle symmetrical tilt grain boundaries (LASTGBs) with θ=8.4° at different temperatures is shown in Fig. 4, presenting that the structure of dislocation pairs at grain boundaries is substantially the same whether at low or high temperatures. On the grain boundary of the same side, two different types of dislocation pairs are alternately arranged (I, II or III, IV) with a total of 10 dislocation pairs. Each dislocation pair is composed of two edge-type dislocations with an angle of 60° [48] (the local enlarged image and their vector direction are shown in Figs. 4(c, d), respectively). LUCADAMO and MEDLIN [49] used TEM to observe the formation mechanism of dislocation array during the growth process at high temperature. It was found that the dislocations were arranged at equal intervals on the twin boundary and remain straight. This result is consistent with our simulation results in Fig. 4. Combined with Fig. 2, the directions of extra half atom arrays of Type I, II, III and IV are n₄+n₅, n₄+n₃, n₁+n₆, and n₁+n₂, respectively. With the rise of the temperature, it is not difficult to find that the dislocation pairs preferentially produce lattice softening on the GBs. The main feature is that liquid phase regions surround the dislocations, but the atomic structure is not destroyed, and only the diminution of atomic order degree around dislocation pair (light blue region) occurs. This phenomenon is consistent with the experimental results. For example, pre-melting of bulk colloidal crystals was caused by defects (dislocation, vacancy, etc) using real-time video microscopy [6] and the premelting of single crystal copper was induced by dislocation motion and dislocation interactions under shock compression [50].

Table 1 Parameters for sample preparation shown in Fig. 1(b)

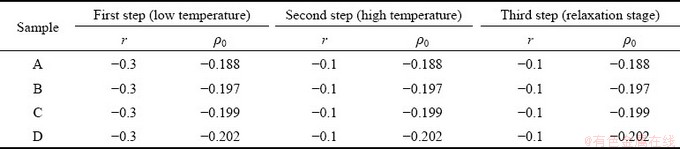
Fig. 3 Formation of low-angle symmetric tilted grain boundaries in bi-crystal solidification process with r=-0.3 and ρ₀=-0.198

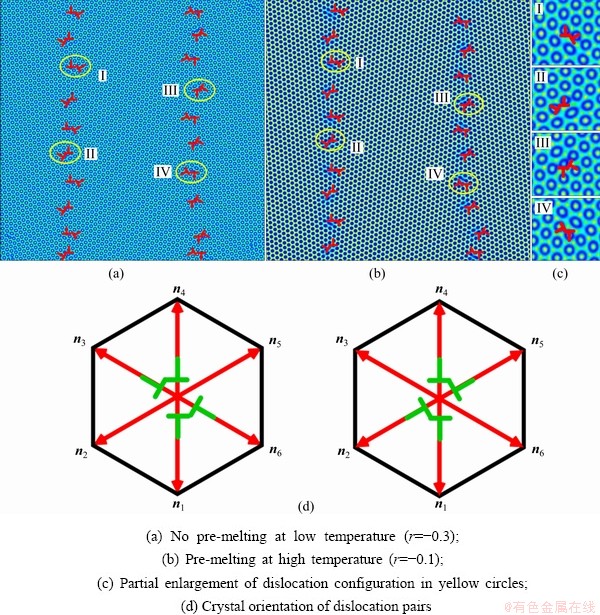
Fig. 4 Snapshots of low-angle GB at θ=8.4° and ρ₀=-0.188

3.2 Generation and evolution of GBPM

Figure 5 shows the early evolution process of liquid pools in the GBPM region, which can be divided into three stages. In the first stage, the stable grain boundaries form at low temperatures, which are composed of a series of edge dislocation pairs at a certain distance. Besides, their specific structures are similar to Fig. 4. Figures 5(b-d) present the second stage in which the temperature of Sample C is raised from a low-temperature condition (r=-0.3) to a high-temperature condition (r=-0.1) at a constant rate. With increasing the temperature, the thermal motion of the atoms accelerates, and the dislocations that make up the GBs move under the driving of temperature. Subsequently, when the temperature of the system uniformly increases to r=-0.2, the order of atoms at the dislocation aggregation decreases due to lattice softening. However, the lattice atoms are not destroyed. Accordingly, the atoms at the grain boundaries in Fig. 5(b) are still arranged neatly and the system keeps solid-solid state. In Fig. 5(c), the atomic disorder increases significantly in the pre-melting region (marked with a red circle), which causes those small droplets around dislocation pairs to form at the GBs. That is to say, there is an incubation period in the pre-melting process.

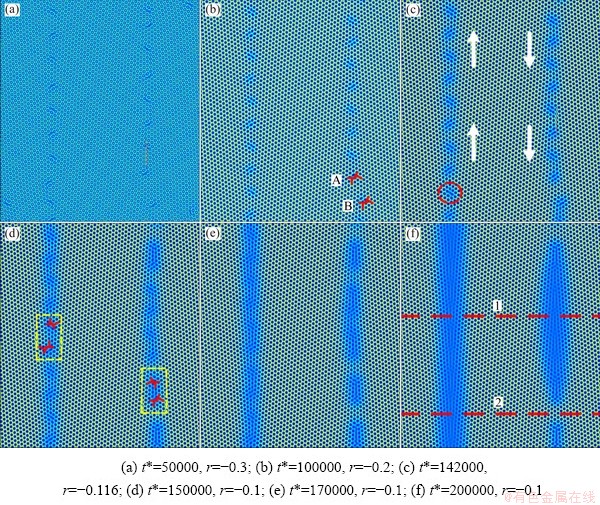
Fig. 5 Evolution of liquid pools of Sample D (ρ₀=-0.199)

In the second stage, as shown in Figs. 5(d, e), under the interaction force among atoms, the dislocation pairs begin to climb along the GBs, leading to the interconnection between adjacent droplets, and a larger liquid pool eventually forms. This phenomenon is similar to the sessile extrinsic grain boundary dislocation arrays after annealing treatment, which is caused by the climbing of dislocations in triple lines [51]. The white arrows present the climbing direction. The dislocation configuration of the liquid pools is composed of four edge dislocations (the yellow box in Fig. 5(d)). In the third stage (Figs. 5(e, f)), it can be observed that with relaxation time prolonging, the liquid pools at the GBs begin to nucleate and grow. The chemical potential energy generated by the phase change drives the movement of dislocations at the grain boundaries. At this point, the solid phase bridge between adjacent liquid pools is broken, forming a uniform liquid phase melting zone. In other words, the expansion of liquid pools is essentially the complete fracture of solid bridges in the two melting zones.

In Fig. 5(b), it is worth noting that the adjacent dislocation pairs A and B at the right GB are mutually repelled because their Burgers vector direction is identical. To present the difference between the two GBs clearly, red dotted lines 1 and 2 are made along with the direction of vertical GBs. Figure 6 demonstrates that the atomic density curves are composed of several peaks and valleys. The wave peaks represent the position of atoms and the wave valleys represent the gap between atoms. Additionally, different amplitude also has different meanings. If the amplitude of the atoms oscillates slightly (violently) within a fixed value range, the atoms are in the liquid-state (solid-state). The S₁ and S₂ represent the solid phase and the liquid phase region at the GBs, respectively. In Fig. 6(a), two S₁ and S₂ regions appear, corresponding to the two liquid phase regions at the GBs of the red dotted line 1 in Fig. 5(f). However, there only exists one S₂ region in Fig. 6(b), due to the fact that a pair of dislocations on the right GB still stays in solid-state, as shown by the red dotted line 2 in Fig. 5(f).

Fig. 6 Atomic density distributions in y-direction inside crystal in Fig. 5(f)

Figure 7 shows the change of free energy of Sample D for 100000 time-steps to raise the temperature and 50000 time-steps to relax. To distinguish the two stages, local amplification is performed at the upper right of the figure. The left side of the blue dotted line presents the heating stage, and the right side indicates the relaxation stage. Intuitively, it appears intuitive that the free energy of the system tends to flat overall in the heating stage, maybe because as the temperature increases, the attractive force between adjacent dislocation pairs does not work. At this time, the dislocation drags the droplets closer to each other and thus the free energy of the system decreases. Meanwhile, with temperature rising, it is easier for atoms to overcome the diffusion barrier, providing a powerful condition for dislocation climbing. The climbing process can release the distortion energy effectively to reduce the energy of the system. During the heat preservation stage, the free energy of the system remains unchanged because the distortion energy in the high-temperature area can be stored, which can thus provide the energy for the expansion of the subsequent liquid pools.

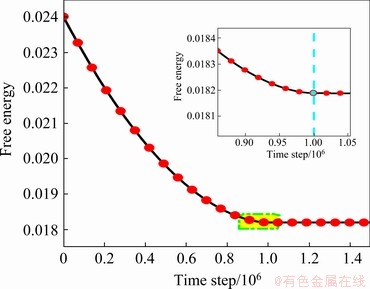
Fig. 7 Free energy curve of Sample C (ρ₀=-0.199)

3.3 Evolution of liquid pools at different ρ₀

Figure 8 shows the evolution of liquid pools of Samples A, B, C and D at different average atomic density ρ₀. For Sample A with high average atomic density, the independent dislocation pairs surrounded by a single liquid phase region gradually form at the GBs. At this point, the atoms at the GBs remain in a solid-solid state. When the time step is 100000, small droplets of Sample B occur at the dislocation aggregation. Subsequently, due to the different directions of the Burgers vector, adjacent small droplets attract each other in the same GB. Eventually, two droplets merge into an elliptical liquid pool. For Sample C, as the average atomic density decreases, the appearance of the liquid pool can relax some lattice distortion. At this time, the fracture of the solid bridge connecting adjacent liquid pools leads to the formation of a homogeneous liquid phase (marked with a red dashed line in Fig. 8(c₂)). In Sample D, the liquid phase continuously devours the surrounding solid phase with the increase of time step, making its area enlarged. Briefly, at the same r, the atomic density of the solid phase is larger. When r is reduced, atoms of GBs diffuse violently and liquid phase forms easily.

Fig. 8 Influence of average atomic density on evolution of liquid pools (Samples A, B, C and D)

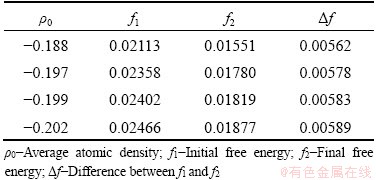
The energy analysis of the evolutionary process for liquid pools is performed and the energy-time curves are illustrated in Fig. 9. It is not difficult to understand that the variation trend of free energy curves at different average atomic densities is consistent, which is firstly decreased and then stabilized. To plainly describe the energy change in the initial stage, the curve of the initial stage is enlarged locally and the specific data are presented in Table 2, showing that the energy of the initial stage is approximately in the range of 0.21-0.24. As the average atomic density increases, both the initial energy and diffusion rate of atoms slow down, and thus the crystal phase characteristics of atoms at GBs become more obvious. Therefore, when the system evolves to an equilibrium state, it becomes more difficult to induce pre-melting, and the system remains in solid state, such as Sample A. When ρ₀ decreases from -0.188 to -0.202, the difference of free energy changes from 0.00562 to 0.00589, indicating that as ρ₀ decreases, the energy declines faster and the atoms can diffuse more fully within a shorter time. As a result, the smaller barrier of the adjacent droplets combines, suggesting that it is easier to form a uniform liquid phase and the width of liquid pools is larger.

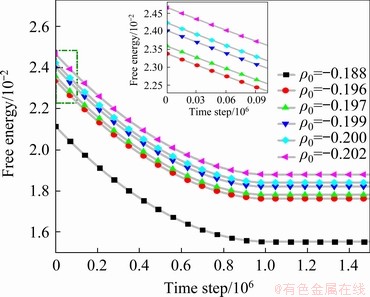
Fig. 9 Free energy curves at different average atomic densities for r=-0.1

Table 2 Free energy values at different ρ₀

4 Discussion

4.1 Thermodynamic analysis

In this work, the excess mass theory [22] is used to calculate the width of liquid pools. The total mass of the system simulated is conserved. However, the chemical potential of system is changed. Thus, the excess mass theory can be transformed into a chemical potential change at the GBs to define the width of liquid pools.

The dimensionless chemical potential in the PFC model is defined as

            (6)

The liquid pools width (w) can be expressed in the following form:

                      (7)

where y is the length perpendicular to the GBs.  u_l(ρ) (u_s(ρ)) stands for the chemical potential of the liquid (solid) phases at the same density. To facilitate the correspondence between different densities and temperature states, u is redefined as ρ₀:

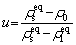                            (8)

where ρ₀ is the average atomic density of the liquid phase, which needs to be set in advance. 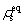 and 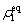 indicate the density of the solid phase and the liquid phase at a fixed r, respectively.

As shown in Fig. 10, the curve generally shows an increasing tendency. To correspond to the atomic microstructure topography, the curve is divided into three stages (I, II and III). Stage I has a negative value, indicating that there is no uniform liquid phase in this stage, and the GBs remain in solid state, such as Sample A. Stage II is expressed as a positive value, which indicates that a significant pre-melting phenomenon has occurred. In this stage, with the decrease of ρ₀, the thermal motion of atoms is intensified and the lattice distortion energy at GBs becomes large, which induces pre-melting. At this point, the system gradually transits from solid-state to small droplet state and then to liquid pool state, as shown in Sample B. In Stage III, the adjacent liquid pools extend to the opposite direction to merge with each other, thereby forming a uniform liquid phase. Consequently, the width of liquid pools increases relatively slowly during this stage, as shown by Samples C and D.

Fig. 10 Change of liquid pools width w with ρ₀

4.2 3-D simulation

At the same spatial scale, the computing space and time needed to change from two-dimensional matrix to three-dimensional matrix increase exponentially. To save calculation time and space, the selected simulation area is 128×128×128. At the same time, Grains 1 and 2 are set in 1x<46 and 82x<128, respectively, and a liquid region with the volume of 36×128×128 is set in the middle, as shown in the blue region in Figs. 11(a₁, a₂). The initial average atom density is ρ₀=-0.202. It can be seen from Fig. 11 that, the grains on both sides continuously swallow the supercooled liquid phase in the middle driven by free energy, thus forming the three-dimensional structure of Fig. 11(b₁). Due to the different orientations of Grains 1 and 2, it is easy to cause extra half atoms during the collision, resulting in dislocations in the yellow circle. As the temperature increases, the atoms in the box in Fig. 11(b₂) soften. When the temperature rises to r=-0.1, the pre-melting phenomenon shown in Fig. 11(c₂) appears. That is to say, the overall evolution law is consistent with the two- dimensional results, which verifies the correctness of the two-dimensional simulation results.

4.3 High-temperature strain action

The grains will deform under the external stress, causing the morphology of pre-melting  zone and dislocation to change. The isovolumic assumption for the deformation process of the two-dimensional system is adopted [52]. The dimensionless strain rate 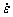 is 6×10^-6.

S=△x·△y=△x′×△y′                       (9)

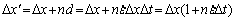          (10)

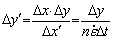                           (11)

where △x and △y are the initial space steps, △x′ and △y′ are the deformed space steps.

The morphology of the high-temperature pre-melting zone and the dislocation evolution mechanism are shown in Fig. 12 under the action of external stress. Here, the vertical dislocations are ignored to more intuitively display the movement of the dislocation and the change of the pre-melting zone induced by the external strain. It can be seen from Figs. 12(a-d) that the oblique dislocations with the same Burgers vectors on the original grain boundaries begin to separate two sub boundaries (III and IV) through sliding motion, as shown by the black dotted line. The splitting of the original grain boundary occurs in the nucleation of deformed grains to form a gap between two sub boundaries. In this case, new deformed Grains 3 and 4 form between the original grain boundaries and the sub-grain boundaries in Fig. 12(b). It seems intuitive that in this temperature range, the morphology of the pre-melting zone is not changed by the applied stress, and the pre-melting zone disappears with the annihilation of the grain boundary. This indicates that the pre-melted regions caused by lattice distortion weakens the interaction between atoms around and reduces the lattice resistance (Peierls Nabarro forces) required for the whole slip process. MOMPIOU et al [53] observed the whole process of annihilation of aluminum films by in situ transmission electron microscopy. In the process of grain shrinkage, dislocation emission was often related to the formation of sub-crystal due to stress concentration, and the final annihilation was completed. A similar phenomenon also exists in our PFC simulation.

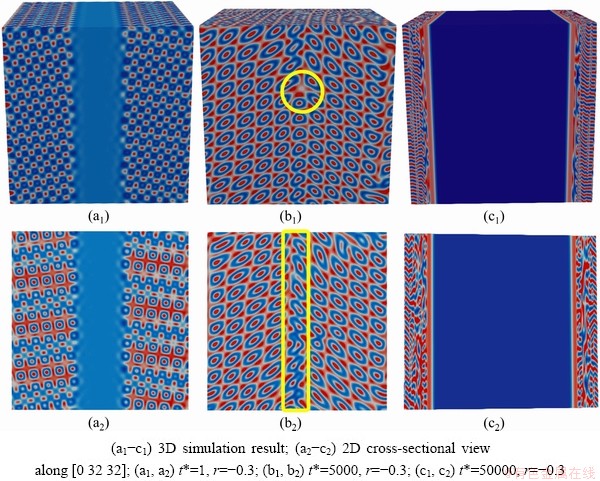
Fig. 11 Schematic diagram of 3-D simulation results

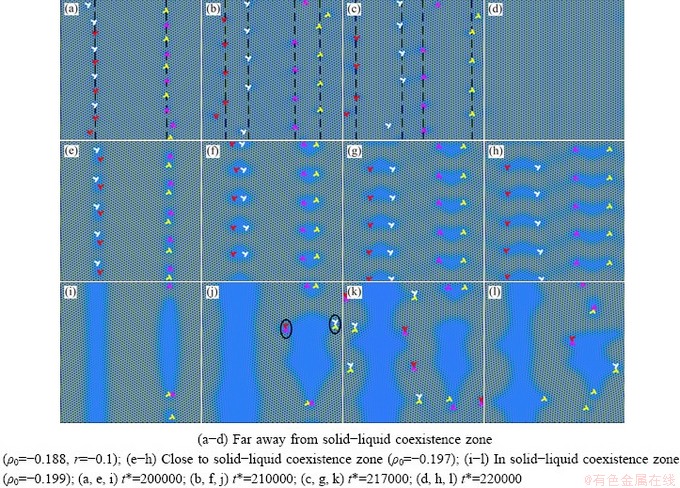
Fig. 12 Evolution of pre-melting zone induced by external strain

The dislocation evolution in the high- temperature pre-melting zone induced by external stress close to the solid-liquid coexistence temperature is illustrated in Figs. 12(e-h). It can be seen that the dislocations in those zones migrate and annihilate, and the expansion, connection and fracture of the pre-melting zones appear due to the interaction of dislocations. In the whole process, the morphology in the pre-melting area changes from small droplet shape to sector shape, to heart shape, to wave shape, and to complete crystal grains.

In the solid-liquid coexistence temperature range, due to the obvious lattice softening, a uniform liquid film forms, which leads to the intensification of atomic thermal motion. This phenomenon not only facilitates the migration of atoms, but also promotes the initiation of new dislocations, as shown by the black ellipses in Figs. 12(i-l). Under the action of the external stress, the dislocation pairs with the opposite Burgers vectors are annihilated, forming a dendritic or inverted pyramid microscopic morphology, as shown in Fig. 12(i). During the entire evolution process, new dislocations sprout and annihilate continuously, making the atomic lattice in the pre-melting zone distorted, which results in the change in the dislocation configuration, number and direction. However, the pre-melting zones do not disappear and complete grains can not form. WANG et al [54] adopted Voronoi clusters (VCs) analysis and dislocation extraction algorithm (DXA) and found that in the tensile process, the pre-existing dislocations would accelerate the formation of larger He bubbles, which increased plasticity and promoted dislocation multiplication. In our PFC simulation, dislocation multiplication also exists. In conclusion, the morphology of the initial remelting zones plays a decisive role in the evolution of dislocation mechanism under high-temperature stress in the later stage.

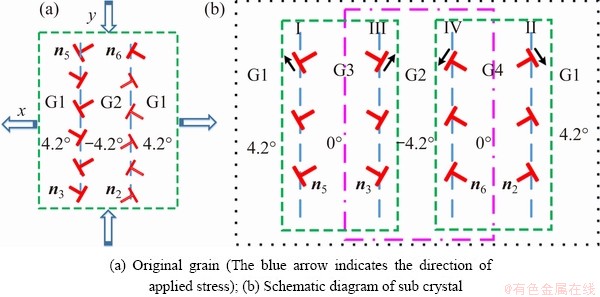
Fig. 13 Schematic diagrams of sub-grain nucleation

5 Conclusions

(1) A double-crystal structure is established and low-angle symmetric tilted grain boundaries (LASTGB) with θ=8.4° are formed. Two types of edge dislocation pairs are alternately arranged on each grain boundary (I, II or III, IV respectively) with a total of 20 dislocation pairs. Both two-dimensional and three-dimensional simulation results show that the pre-melting phenomenon first occurs at the dislocation aggregation due to the lattice atom softening, which is consistent with previous experimental results about defect-induced pre- melting.

(2) The early evolution process of the liquid pools at GBs is mainly divided into three stages, with four structural changes. In the first stage, the GBs gradually change from the original solid-solid state to the small droplet state. In the second stage, adjacent droplets with different Burgers vector directions merge into a larger liquid pool during the climbing process. In the third stage, the adjacent liquid pools are further connected to form a uniform liquid phase melting zone. The enlargement of liquid pools causes the complete fracture of the solid bridge in two melting regions.

(3) The degree of liquid pools pre-melting is diverse under different average atomic densities (ρ₀). The decrease of ρ₀ inhibits the crystalline phase characteristics of atoms at dislocation aggregation and accelerates the transition to the disordered liquid phase, which contributes to the formation of liquid pools and the increase of the width. Hence, ρ₀ is inversely proportional to the width of liquid pools.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (51774254, 51774253, 51701187, 51674226, 51804279, 51801189); The Science and Technology Major Project of Shanxi Province, China (20191102008); Platform and Talent Project of Shanxi Province, China (201805D211036); Guiding Local Science and Technology Development Projects by the Central Government of China (YDZX20191400002796); Transformation of Scientific and Technological Achievements Special Guide Project of Shanxi Province, China (201804D131039).

References

[1] AVVAL N, ASADI E. Thermodynamics of FCC metals at melting point in one-mode phase-field crystals model [J]. Computational Materials Science, 2018, 145: 224-234.

[2] LI Xin-hua, ZHAO Huan-huan, MA Zong-qing, YU Li-ming, LIU Chen-xi, GUO Qian-yin, LIU Yong-chang. The formation and evolution mechanism of amorphous layer surrounding Nb nano-grains in Nb-Al system during mechanical alloying process [J]. Journal of Alloys and Compounds, 2019, 779: 175-182.

[3] LU Yan-Li, HU Ting-Ting, LU Guang-Ming, CHEN Zheng. Phase-field crystal study of segregation induced grain- boundary premelting in binary alloys [J]. Physica B, 2014, 451: 128-133.

[4] PENG Ying-ying, LU Yan-Li, CHEN Zheng, YU Geng-geng. A binary phase field crystal study for phase segregation of liquid phase heteroepitaxial growth [J]. Computational Materials Science, 2016, 123: 65-69.

[5] ADLAND A, KARMA A, SPATSCGEK R, BUTA D, ASTA M. Phase-field-crystal study of grain boundary pre-melting and shearing in bcc iron [J]. Physical Review B, 2013, 87: 024110.

[6] ALSAYED A M, ISLAM M F, ZHANG J, COLLINGS P J, YODH A G. Premelting at defects within bulk colloidal crystals [J]. Science, 2005, 309: 1207-1211.

[7] PUSEY P N. Freezing and melting: Action at grain boundaries [J]. Science, 2005, 309: 1198-1201.

[8] CHAUDRON G, LACOMBE P, YANNAQUIS N. Intergranular corrosion of pure aluminium in relation to the behaviour of grain-boundaries during melting [J]. Nature, 1948, 162: 854-855.

[9] GORKAYA T, MOLODOV K D, MOLODOV D A, GOTTSTEIN G. Concurrent grain boundary motion and grain rotation under an applied stress [J]. Acta Materialia, 2011, 59: 5674-5680.

[10] MAEDA K, NIITSU A, MORITO H, SHIGA K, FUJIWARA K. In situ observation of grain boundary groove at the crystal/melt interface in Cu [J]. Scripta Materialia, 2018, 146: 169-172.

[11] STRAUMAL B B, KOGTENKOVA O A, MURASHKIN M Y, BULATOV M F, CZEPPE T, ZIEBA P. Grain boundary wetting transition in Al-Mg alloys [J]. Materials Letters, 2017, 186: 82-85.

[12] ELDER K R, KATAKOWSKI M, HAATAJA M, GRANT M. Modeling elasticity in crystal growth [J]. Physical Review Letters, 2002, 88: 245701.

[13] ELDER K R, GRANT M. Modeling elastic and plastic deformations in nonequilibrium processing using phase field crystals [J]. Physical Review E, 2004, 70: 051605.

[14] OLMSTED D L, BUTA D, ADLAND A, FOILES S M, ASTA M, KARMA A. Dislocation-pairing transitions in hot grain boundaries [J]. Physical Review Letters, 2011, 106: 046101.

[15] LIU Huan, GUO Yong-bo, ZHAO Peng-yue, SU Dian-cheng. Research progress on nano-machining mechanism of metallic materials based on molecular dynamics simulation [J]. Transactions of Nonferrous Metals Society of China, 2019, 29: 1263-1269.

[16] TRAUTT Z T, ADLAND A, KARMA A, MISHIN Y. Coupled motion of asymmetrical tilt grain boundaries: Molecular dynamics and phase field crystal simulations [J]. Acta Materialia, 2012, 60: 6528-6546.

[17] ZHAO Yu-hong, TIAN Xiao-lin, ZHAO Bao-jun, SUN Yuan-yang, GUO Hui-jun, DONG Meng-yao, HU Liu, WANG Xiao-jing, GUO Zhan-hu, AHMAD U, HOU Hua. Precipitation sequence of middle Al concentration alloy using the inversion algorithm and microscopic phase field model [J]. Science of Advanced Materials, 2018, 10: 1793-1804.

[18] YU An-shan, YANG Xiang-jie, GUO Hong-min. Phase field lattice Boltzmann model for non-dendritic structure formation in aluminum alloy from LSPSF machine [J]. Transactions of Nonferrous Metals Society of China, 2020, 30: 559-570.

[19] ZHENG Xiao-juan, ZHAO Yu-hong, HOU. Hua, JIN Yu-chun, MA Qing-shuang, TIAN Jin-zhong. Effect of elastic strain energy on L1₂ phase precipitation simulated by using microscopic phase-field method [J]. The Chinese Journal of Nonferrous Metals, 2017, 27: 2098-2014. (in Chinese)

[20] EMMERICHA H, LOWENB H, WITTKOWSKI R, GRUHN T, TOTHC G I, TEGZEC G, GRANASY L. Phase- field-crystal models for condensed matter dynamics on atomic length and diffusive time scales: An overview [J]. Advances in Physics, 2012, 61: 665-743.

[21] GAO Ying-jun, LU Yu-jiang, KONG Ling-yi, DENG Qian-qian, HUANG Li-lin, LUO Zhi-rong. Phase field crystal model and its application for microstructure evolution of materials [J]. Acta Metallurgica Sinica, 2018, 54: 278-292.

[22] YAMANAKA A, MCREYNOLDS K, VOORHEES P W. Phase field crystal simulation of grain boundary motion, grain rotation and dislocation reactions in a BCC bicrystal [J]. Acta Materialia, 2017, 133: 160-171.

[23] MELLENTHIN J, KARMA A, PLAPP M. Phase-field crystal study of grain-boundary premelting [J]. Physical Review B, 2008, 78: 184110.

[24] ADLAND A, KARMA A, SPATSCGEK R, BUTA D, ASTA M. Phase-field-crystal study of grain boundary premelting and shearing in bcc iron [J]. Physical Review B, 2013, 87: 024110.

[25] LU Yan-li, MU Hong, HOU Hua-xin, CHEN Zheng. Phase field crystal simulation for the premelting and melting of grain boundary [J]. Acta Metallurgica Sinica, 2013, 49: 358-364.

[26] GAO Ying-jun, DENG Qian-qian, LIU Zhe-yuan, HUANG Zong-ji, LI Yi-xuan, LUO Zhi-rong. Modes of grain growth and mechanism of dislocation reaction under applied biaxial strain: Atomistic and continuum modeling [J]. Journal of Materials Science & Technology, 2020, 49: 236-250.

[27] HU Shi, WANG Song. The influences of crystal orientation and crack interaction on the initiation of growth and propagation mode of microcrack: A phase-field-crystal study [J]. Physica B: Condensed Matter, 2019, 552: 104-109.

[28] GAO Ying-jun, DENG Qian-qian, QUAN Si-Long, ZHOU Wen-quan, HUANG Chuang-gao. Phase field crystal simulation of grain boundary movement and dislocation reaction [J]. Frontiers of Materials Science, 2014, 8: 176-184.

[29] GUO Hui-jun, ZHAO Yu-hong, SUN Yuan-yang, TIAN Jin-zhong, HOU Hua, QI Ke-wu, TIAN Xiao-lin. Phase field crystal study of grain boundary structure and annihilation mechanism in low-angle grain boundary [J]. Superlattices and Microstructures, 2019, 129: 163-175.

[30] LU Y L, HU T T, LU G M, CHEN Z. Phase-field crystal study of segregation induced grain-boundary premelting in binary alloys [J]. Phys B: Condens Matter 2014, 451: 128-133.

[31] GAO Ying-jun, HUANG Li-lin, DENG Qian-qian, ZHOU Wen-quan, LUO Zhi-rong, LIN Kui. Phase field crystal simulation of dislocation configuration evolution in dynamic recovery in two dimensions [J]. Acta Materialia, 2016, 117: 238-251.

[32] KONG Ling-yi, GAO Ying-jun, DENG Qian-qian, LUO Zhi-rong, LU Yu-jing. A study of strain-driven nucleation and extension of deformed grain: Phase field crystal and continuum modeling [J]. Materials, 2018, 11: 1805.

[33] HOYT J J, OLMSTED D, JINDAL S, ASTA M, KARMA A. Method for computing short-range forces between solid-liquid interfaces driving grain boundary premelting [J]. Physical Review E, 2009, 79: 020601.

[34] LIANG Zun, DU Hua, LIANG Hong-tao, YANG Yang. Grain boundary premelting of monolayer ices in 2D nano-channels [J]. Molecular Physics, 2019, 117: 1-8.

[35] BERRY J, ELDER K R, GRANT M. Melting at dislocations and grain boundaries: A phase field crystal study [J]. Physical Review B, 2008, 77: 224114.

[36] ZHAO Yu-hong, DENG Shi-jie, LIU Hu, ZHANG Jiao-xia, GUO Zhan-hu. HOU Hua. First-principle investigation of pressure and temperature influence on structural, mechanical and thermodynamic properties of Ti₃AC₂ (A=Al and Si) [J]. Computational Materials Science, 2018, 154: 365-370.

[37] WEN Zhi-qin, HOU Hua, TIAN Jin-zhong, ZHAO Yu-hong, LI Hui-jun, HAN P D. First-principles investigation of martensitic transformation and magnetic properties of Ni₂XAl (X=Cr, Fe, Co) Heusler compounds [J]. Intermetallics, 2018, 92: 15-19.

[38] ZHAO Yu-hong, QI Lei-Jin, WANG Yu-chun, TIAN Kun, HAN Jin-zhong. The structural, elastic, electronic properties and Debye temperature of D0₂₂-Ni₃V under pressure from first-principle [J]. Journal of Alloys and Compounds, 2015, 647: 1104-1110.

[39] PROVATAS N, DANTZIG J A, ATHREYA B, CHAN P, STEFANOVIC P, GOLDENFELD N, ELDER K R. Using the phase-field crystal method in the multi-scale modeling of microstructure evolution [J]. JOM, 2007, 59: 83-90.

[40] STEFANOVIC P. HAATAJA M, PRDVATAS N. Phase-field crystals with elastic interactions [J]. Physical Review Letters, 2006, 96: 22504.

[41] ELDER K R, PROVATAS N, BERRY J, STEFANOVIC P, GRANT M. Phase-field crystal modeling and classical density functional theory of freezing [J]. Physical Review B, 2007, 75: 794-802.

[42] SWIFT J, HOHENBERG P C. Hydrodynamic fluctuations at the convective instability [J]. Physical Review A, 1977, 15: 319-328.

[43] BERRY J, GRANT M, ELDER K R. Diffusive atomistic dynamics of edge dislocations in two dimensions [J]. Physical Review E, 2006, 73: 031609.

[44] MOROZOV N F, OVIDKO I A, SHEINERMAN A. Special rotational deformation as a toughening mechanism in nanocrystalline solids [J]. Journal of the Mechanics and Physics of Solids, 2010, 58: 1088-1098.

[45] CHAN P Y, GOLDENFOLD N, DANTZIG J. Molecular dynamics on diffusive time scales from the phase-field- crystal equation [J]. Physical Review E, 2009, 79: 035701.

[46] CHENG M, WARREN J A. An efficient algorithm for solving the phase field crystal model [J]. Journal of Computational Physics, 2008, 227: 6241-6248.

[47] GOMEZ H, XESUS N. An unconditionally energy-stable method for the phase field crystal equation [J]. Computer Methods in Applied Mechanics and Engineering, 2012, 249-252: 52-61.

[48] HIRTH J P, LOTHE J. Theory of dislocation [M]. New York: McGraw-Hill, 1968.

[49] LUCADAMO G, MEDLIN D L. Dislocation emission at junctions between Σ=3 grain boundaries in gold thin films [J]. Acta Materialia, 2002, 50: 3045-3055.

[50] WANG Liang, CAI Yang, HE An-Ming, LUO Sheng-Nan. Second yield via dislocation-induced premelting in copper [J]. Physical Review B, 2016, 93: 174106.

[51] NAZAROV A A. Kinetics of grain boundary recovery in deformed polycrystals [J]. Interface Science, 2000, 8: 315-322.

[52] HIROUCHI T, TAKAKI T, TOMITA Y. Development of numerical scheme for phase field crystal deformation simulation [J]. Computational Materials Science, 2009, 44: 1192-1197.

[53] MOMPIOU F, LEGROS M, RADETIC T, DAHMEN U, GIANOLA D S, HEMKER K J. HEMKER. In situ TEM observation of grain annihilation in tricrystalline aluminum films [J]. Acta Materialia, 2012, 60: 2209-2218.

[54] WANG Jin, YU Li-ming, HUANG Yuan, LI Hui-jun, LIU Yong-chang. Effects of dislocation density, temperature and Cr concentration on helium behavior in α-Fe [J]. Computational Materials Science, 2019, 160: 105-114.

晶体相场法模拟晶界预熔区液相熔池的演化

田晓林，赵宇宏，彭敦维，郭庆伟，郭 震，侯 华

中北大学 材料科学与工程学院，太原 030051

摘  要：预熔是指晶体在低于熔点温度时，晶界处预先出现类似液体而块体仍为晶体状的现象。采用晶体相场法研究原子密度对晶界预熔的影响。结果表明：晶界处液相熔池的早期演化主要涉及4个形态特征：固-固状态→小液滴状态→较大的液相熔池→均质熔融层。通过对比不同平均原子密度下的微观结构和能量变化，表明平均原子密度对液相池的形态特征敏感。二维与三维模拟结果表明，平均原子密度的降低能抑制刃型位错聚集区域中原子的结晶相特征，这有助于液相熔池的形成。从热力学的角度验证平均原子密度与液相熔池宽度之间的关系，在一定程度上为后续施加高温应变提供前提条件。

关键词：晶体相场法；预熔；刃型位错；液相熔池

(Edited by Bing YANG)

Corresponding author: Yu-hong ZHAO; Tel: +86-15035172958; E-mail: zhaoyuhong@nuc.edu.cn

DOI: 10.1016/S1003-6326(21)65570-X

1003-6326/ 2021 The Nonferrous Metals Society of China. Published by Elsevier Ltd & Science Press