DOI: 10.11817/j.issn.1672-7207.2017.02.020
模糊理论在软件项目风险评估中的应用
唐爱国1, 2, 3,胡春华1, 2, 3
(1. 湖南商学院 移动商务智能湖南省重点实验室,湖南 长沙,410205;
2. 湖南商学院 计算机与信息工程学院,湖南 长沙,410205;
3. 湖南商学院 湖南省移动电子商务协同创新中心,湖南 长沙,410205)
摘要:为有效防范软件项目失败风险,必须加强软件项目风险管理的意识和能力。在对软件项目风险管理过程分析的基础上,提出一种基于模糊理论的软件风险评估模型,使用模糊性语言评估风险后果及损失,度量多种风险对某种风险后果的组合影响以及单个风险对整体后果的综合影响,解决专家评估的不确定性问题,增强软件项目风险的预测和应变能力,为有效地降低风险发生概率、提高软件开发成功率提供了一种新途径。
关键词:软件项目;风险管理;风险评估;模糊理论
中图分类号:TP311 文献标志码:A 文章编号:1672-7207(2017)02-0411-07
Application of fuzzy theory in software project risk assessment
TANG Aiguo1, 2, 3, HU Chunhua1, 2, 3
(1. Key Laboratory of Hunan Province for Mobile Business Intelligence,
Hunan University of Commerce, Changsha 410205, China;
2. College of Computer and Information Engineering, Hunan University of Commerce, Changsha 410205, China;
3. Mobile E-business Collaborative Innovation Center of Hunan Province,
Hunan University of Commerce, Changsha 410205, China)
Abstract: Considering that many uncertainties always exist in the development and management process of software project, the awareness and ability of software project risk management must be strengthened to effectively prevent the occurrence of the failure. On the basis of the analysis of the software project risk management process, a model based on fuzzy theory in software project risk assessment was proposed. Using the fuzzy language to assess the consequences and the loss of the risk, the model can measure the combination of impact of a certain risk from a variety of risks and the combined effects of the overall consequences from individual risk, which resolves the uncertainty of expert assessment, enhances the prediction and response capabilities of the software project risk and thus it provides a new way to effectively reduce the risk probability and increases the rate of the success of the software development.
Key words: software project; risk management; risk assessment; fuzzy theory
软件项目风险是指在软件开发过程中遇到的费用、进度与功能等方面的问题以及这些问题对软件项目的影响。对软件项目进行风险评估是要找出导致项目需求不明确、不能按进度计划及时间交付、产品质量存在缺陷、开发费用超支等各种不良后果的风险因素,对风险因素及可能造成的后果和危害进行定性和定量分析,从而为软件项目管理人员、软件开发者、软件产品用户等提供有效的风险控制方案和措施,使其对软件项目的损失或影响降低到最低程度[1]。随着软件项目的复杂化和规模化,软件开发与管理变得越来越复杂,人们对软件风险的影响和控制越来越重视。但在软件开发中进行完整的规范化风险评估还很不足,主要表现在软件项目风险管理的研究和实践起步较晚,风险管理停留在概念层面,缺乏具体管理制度和方法支持;软件企业主要依靠项目管理人员的个人经验,实行以定性分析为主的风险管理,风险管理水平参差不齐,具有一定的随意性。由于在风险管理过程中缺乏定量分析方法,因此,有关项目资料和数据的收集具有盲目性,从而导致该领域的知识不能得到有效积累,影响了软件项目风险管理水平的提高[2-3]。为此,本文作者提出基于模糊理论的软件项目风险评估模型,使用模糊性语言评估风险损失,通过模糊数的语义距离计算还原评估结果,解决评估中的不确定性问题,可有效地降低风险发生概率。
1 软件项目风险管理过程
软件项目的开发存在各种风险,有些风险甚至是灾难性的。识别风险并制定风险计划,以最大限度地降低风险对项目的影响,这称为风险管理。软件项目风险管理是指在风险在对软件项目产生不良影响之前,识别、处理并消除风险的源头。软件项目风险管理过程分为风险评估和风险控制两大部分,其中风险评估分为风险识别、风险分析、风险计划3个过程,风险控制则包括风险跟踪与风险应对2个过程[4-7]。软件项目风险管理过程如图1所示。
风险评估是软件项目风险管理的核心和基础,直接影响软件项目风险管理的其他过程,甚至影响软件项目效果。
2 模糊理论
2.1 模糊集的定义及其表示
将二值逻辑进行模糊推广而建立的模糊逻辑接近人的形象思维方式,非常适合定性分析与推理,同时具有较强的处理自然语言的能力。为了定量地刻画模糊概念和模糊现象,引入模糊集合这一概念[8],模糊集的表示方法如下:
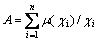 或者
或者 (1)
(1)
其中:有限集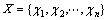 ;
;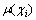 为
为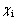 对A的隶属度。若某个
对A的隶属度。若某个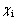 对A的隶属度
对A的隶属度 ,则可略去。
,则可略去。
模糊数的形式有很多种,其中最常用的是三角模糊数。三角模糊数Z∈[0,1]可以表示为
Z=(l,m,n) (2)
其中:l表示最悲观值;m表示最可能值;n表示最乐观值;隶属函数 。
。
2.2 语义距离与语义还原
由模糊计算得出的结果为模糊数形式,为适合于人的思维习惯,需将其还原为自然语言表述,即语义相近或语义还原。为达到这一目的,需要找到与预定模糊集之间最接近的模糊术语。为便于理解且容易在计算机上实现,采用“最适度(best fit)”方法。该方法是基于Dubois和Prade的两集合间的欧几里德距离,结合ROSS提出的改进欧几里德方法[9],可定义2个模糊集合间的距离如下。
设E和F分别为论域X上相应的模糊概念的模糊集,i取0或1,n表示α-截集的个数,则欧几里德距离为

图1 软件项目风险管理过程
Fig. 1 Processes of software project risk management
 (3)
(3)
取计算的模糊数与预设模糊集的距离最小者,将其还原为自然语言表达。
2.3 模糊理论与风险评估
风险评估技术依据项目所能提供的经验数据数量及信息详细程度,可分为定性评估和定量评估2种。但无论采用哪种方法,在应用软件项目的实际开发中,风险评估往往因为经验数据不足而更多地依赖于人为评估。同时,评估专家所使用的评估语言本身带有一定的模糊性,很难用传统的数理统计计算风险的各个参数,这就给评估带来了更大困难[10]。但模糊理论采用隶属函数的描述方法,运用多值逻辑可以很好地解决风险评估中的不确定性和模糊问题,主要体现在以下3个方面。
1) 风险后果的评估。首先,在识别软件项目中的风险后,使用模糊评语定义风险对后果影响(预设)的模糊评语集;然后,将该集合表示成模糊数的形式参与计算。
2) 风险影响计算。结合风险分析网络中计算的风险概率计算风险当量、组合风险影响和综合风险影响。
3) 评估结果还原。为了使风险评估结果更为直观,需将最终的多维评估结果还原成自然语言表述形式,通过计算评估结果与既定模糊评语间的距离进行语义还原。
3 软件项目风险评估模型
3.1 模型设计
软件项目风险评估模型以模糊理论为基础,领域专家使用模糊语言进行评估,通过模糊数的截集运算计算风险的概率及影响,计算风险的综合影响并进行排序,使用模糊数间的语义距离将评估结果转化为自然语言描述[11-13]。软件项目风险评估模型如图2所示。
3.2 风险发生概率评估
风险的评估过程是依据风险因子节点进行的,风险分析网络是表示变量间概率依赖关系的有向无环图,每个节点都对应1个条件概率分布表(CPT),指明了该变量与父节点之间概率依赖的数量关系[14]。风险发生概率的评估步骤如下。
1) 定义风险发生概率的模糊评语集。在缺乏项目历史数据情况下,领域专家将使用“不可能”和“可能”等模糊性语言来评价风险发生的概率,即模糊评语集Hq={极不可能,不可能,中等,可能,很可能}。
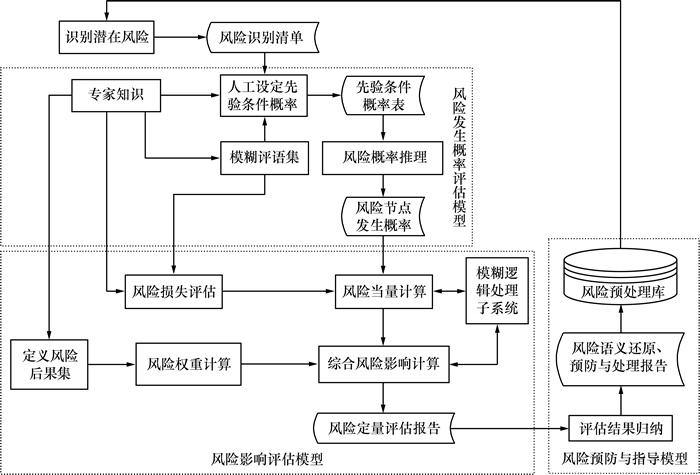
图2 软件项目风险评估模型
Fig. 2 Risk assessment model of software project
2) 风险发生概率评估是指专家使用模糊评语集Hq,设定风险分析网络中的条件概率和先验概率,形成条件概率分布表。
3) 根据风险分析网络结构和条件概率分布表进行风险发生概率推理,计算出各个风险节点的概率综合评估矩阵Pcp=[P1,,P2,…,Pn]。
4) 在评估进行过程中,随着新信息(即证据)的获得,可实时进行网络的传播与更新。
3.3 风险影响评估
风险影响评估包括2部分,即风险损失评估和风险影响综合评估[15]。风险影响的评估步骤如下。
1) 定义风险因素后果集D={D1,D2,…,Dn},风险对后果影响的模糊评语集Hr={极低,低,中等,高,极高}。
2) 风险损失评估。是指专家使用模糊评语集Hq构建模糊专家评估矩阵Ccp,以此来评价各种风险对后果集D造成的影响。
3) 风险权重计算。用风险因素的权重系数向量G=[g1,g2,…,gn]T表示(其中n为风险因素个数,gi为第i类风险因素的相对重要程度)。
4) 风险影响综合评估。风险当量是评估软件风险程度的关键指标,目前的分析方法通常由风险概率与后果的乘积度量单个风险对各风险后果的危害程度。
3.4 风险预防与指导
风险评估完成后,得到一系列由数据或自然语言表述的评估结果,这些结果并不能直观地描述各项评估结果的含义,因此,软件项目风险评估模型中增加了风险预防与指导模型。该模型根据风险分类和风险定量评估报告,对评估结果进行归纳,将本次评估中的风险归类,对每类中的风险进行等级比对,确定其严重程度,给出风险定性分析报告,针对不同级别的风险给出相应的风险解释、预防和控制方案。同时,将本次风险评估结果存入风险预处理库,作为下一个软件项目风险评估的参考依据。
4 模糊理论在风险评估中的应用
软件项目在系统分析和设计环节中经常存在项目计划制定不完善、需求不确定、技术或方法选择不恰当等因素,并且这些因素相互影响大,对风险的评估尤为重要[16]。本文以制造业信息化公共服务平台项目为例,说明在软件项目中利用模糊理论进行风险评估的过程。
4.1 问题描述
制造业信息化公共服务平台属于创新型项目,项目组在研发过程中需求变更频繁,开发人员对开发平台与开发技术难以掌握,对软件性能的提高有较大影响。
在项目启动时实施风险评估,首先识别项目中的风险和风险因子,设定风险关键词,即需求风险、需求变更、技术风险、技术熟悉度、软件复杂性、人员沟通、软件性能以及安全策略等[17]。根据已有案例启动风险案例学习机制,结合专家经验生成评估的风险分析网络,如图3所示。

图3 风险分析网络
Fig. 3 Network of risk analysis
4.2 风险评估
软件项目风险的评估是软件项目风险评估模型中的核心,评估过程分为风险发生概率评估和风险影响评估。在风险分析过程中涉及2个概率,即条件概率和先验概率。条件概率是指事件1已经出现的条件下,事件2发生的概率;先验概率是指根据历史资料或主观判断所确定的各事件发生的概率,该类概率没能经过实验证实,属于检验前概率,所以称为先验概率。
在缺乏项目历史数据的情况下,领域专家使用模糊评语集Hq={极不可能,不可能,中等,可能,很可能}来评价风险发生的概率。根据风险分析网络的拓扑结构以及专家领域知识,遵循风险发生概率的评估步骤,设定各个网络节点的条件概率[18]。图3中软件性能风险节点的CPT设置如表1所示。
表1 软件性能风险节点的CPT设置
Table 1 Software performance risk node CPT settings

用节点变量Xi代替图3所示风险分析网络中的各节点,简化的风险分析网络结构如图4所示。
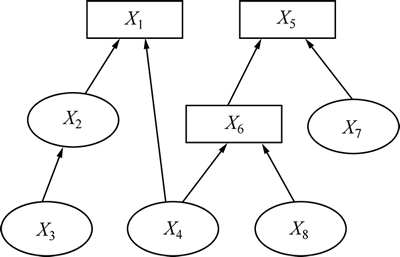
图4 简化的风险分析网络结构
Fig. 4 A simplified risk analysis of network structure
贝叶斯网络以图形表示随机变量间的联合概率,能够处理各种不确定性信息。贝叶斯网络的推理是以贝叶斯概率理论为基础的,不需要外界的任何推理机制。根据贝叶斯网络的形式化分析,则有:
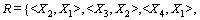
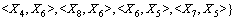 (4)
(4)
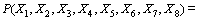

 (5)
(5)
根据条件概率分布表与式(4)和式(5)进行风险发生概率推理,计算各个风险节点的概率综合评估矩阵Pcp=[P1,P2,…,Pn]。
专家根据应用系统特征,设定风险后果集D={进度,成本,软件质量}以及风险对后果影响的模糊评语集Hr={极低,低,中等,高,极高},构建模糊专家评估矩阵Ccp,以此来评价各种风险Ri对制造业信息化服务平台造成的风险损失。模糊专家评估矩阵Ccp由M个风险后果、N类风险组成,任意1个Cij表示第i类风险对第j类风险后果的影响进行的评估。制造业信息化服务平台风险损失评估如表2所示。
根据风险损失评估以及风险节点发生概率,调用风险当量的计算公式,计算风险综合影响Rcp和风险组合影响Rcb的值。
Re=Pcp×Ccp (6)
Rcb=[R1,R2,…,Rm]T;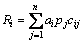 (7)
(7)
Rcp=[R1,R2,…,Rn]/(R1+R2+…+Rn);
 (8)
(8)
得到风险当量的精确值如表3所示。
在不同的项目、环境及资源下,风险因素的重要程度有所不同,用风险因素的权重系数向量G=[gl, g2,…,gn]T表示。gi可由层次分析法(analytic hierarchy process,AHP)法求出,具体方法是:1) 将不同的风险因素列成比较矩阵;2) 按照表4中的1~9标度法进行两两比较;3) 由方根法求其权重,归一化处理得到向量G,并求出一致性指标RC;4) 当RC<0.1时,该比较矩阵满足一致性要求,否则需调整比较矩阵。风险权重计算结果如表5所示。
表2 风险损失评估
Table 2 Loss assessment of risk

表3 风险当量量化数据
Table 3 Equivalent quantized data of risk

表4 1~9标度法及含义
Table 4 1 to 9 scale method and meaning

表5 风险权重计算结果
Table 5 Risk weights for evaluation and calculation results

根据风险损失评估结果和风险权重,计算风险综合影响和组合影响值。经计算,风险综合影响中需求风险占20.61%,技术风险占46.8%,性能风险占32.59%;风险组合影响中对进度的影响占29.81%,对成本的影响占21.67%,对软件质量的影响占44.52%。
采用间接法来计算模糊数间的语义距离,定义模糊数E和F,其中,E为三角模糊数,F为预定的模糊评语。E和F的模糊数分别表示为(l1,m1,n1)和(l2,m2,n2)。Hq,Hr与α-截集的对应关系如表6所示。
表6 三角模糊数及截集对应关系
Table 6 Corresponding relationship between triangular fuzzy number and cut-set

要计算模糊数E与F之间的距离,根据式(3),需计算Emin(i),Fmin(i),Emax(i) 和Fmax(i)(i=a,a取0或1),则有:Emin(0)=l1,Emax(0)=n1,Emin(1)= Emax(1)=m1,Fmin(0)=l2,Fmax(0)=n2,Fmin(1)=Fmax(1)=m2。两模糊数E和F之间的距离为
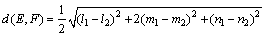 (9)
(9)
风险评估的结果是模糊数形式,为了适合人的思维习惯,需将其还原成自然语言表达。通过计算,语义还原如表7所示。将表7与表2进行对比可以看出:采用本文提出的风险评估方法所得计算结果与专家预设的风险对后果的影响结果具有很大的相似性。
表7 风险语义还原
Table 7 Semantic reduction of risk

5 结论
1) 以模糊理论为基础提出了一种新的软件项目风险评估模型,克服了传统分析方法中定性指标定量评估的难点,通过风险分析网络推理风险发生概率,在很大程度上降低了评估的难度和主观性。
2) 使用模糊性语言评估风险损失,并采用模糊逻辑处理技术计算风险发生概率,解决了专家评估的不确定性问题;通过模糊数的语义距离计算,还原评估结果,为风险的分级提供了依据;根据评估结果,提供风险释义和风险预防措施,在很大程度上避免和减少了风险造成的损失。
3) 该模型具有完善的学习机制,逐步丰富企业自己的风险数据库,在不断学习和修正过程中提高了风险的预测和应变能力。
参考文献:
[1] 曹萍, 陈福集, 张剑. 基于进度的软件外包项目风险优化控制决策[J]. 武汉大学学报(工学版), 2012, 45(3): 385-388.
CAO Ping, CHEN Fuji, ZHANG Jian. Risk optimization control decision-making of software outsourcing project based on schedule[J]. Engineering Journal of Wuhan University, 2012, 45(3): 385-388.
[2] 张进春, 吴超. 基于广义线性模型的概率风险评价方法及其应用[J]. 中南大学学报(自然科学版), 2011, 42(6): 1719-1724.
ZHANG Jinchun, WU Chao. Probabilistic risk assessment method based on generalized linear models and its application[J]. Journal of Central South University (Science and Technology), 2011, 42(6): 1719-1724.
[3] LIU Qin, QIN Wenzhong, MINTRAM R, et al. Evaluation of preliminary data analysis framework in software cost estimation based on ISBSG R9 Data[J]. Software Quality Journal, 2008, 16(3): 411-458.
[4] CHOW T, CAO D. A survey study of critical success factors in agile software projects[J]. Journal of Systems and Software, 2008, 81(6): 961-971.
[5] 高翔, 祝跃飞, 刘胜利, 等. 基于模糊Petri网的网络风险评估模型[J]. 通信学报, 2013, 34(Z1): 126-131.
GAO Xiang, ZHU Yuefei, LIU Shengli, et al. Risk assessment model based on fuzzy Petri nets[J]. Journal on Communications, 2013, 34(Z1): 126-131.
[6] 高晖, 张莉, 李琳. 软件体系结构层次软件适应性预测模型[J]. 软件学报, 2010, 21(9): 2118-2134.
GAO Hui, ZHANG Li, LI Lin. Software flexibility prediction model in software architecture level[J]. Journal of Software, 2010, 21(9): 2118-2134.
[7] 张胜礼, 李永明. 否定知识的代数表示及在模糊系统设计中的应用[J]. 计算机学报, 2016, 39(12): 2527-2545.
ZHANG Shengli, LI Yongming. Algebraic representation of negative knowledge and its application to design of fuzzy system[J]. Chinese Journal of Computers, 2016, 39(12): 2527-2545.
[8] 付钰, 吴晓平, 叶清, 等. 基于模糊集与熵权理论的信息系统安全风险评估研究[J]. 电子学报, 2010, 38(7): 1489-1494.
FU Yu, WU Xiaoping, YE Qing, et al. An approach for information systems security risk assessment on fuzzy set and entropy-weight[J]. Acta Electronica Sinica, 2010, 38(7): 1489-1494.
[9] LEE E S, LI R J. Comparison of fuzzy numbers based on the probability measure of fuzzy events[J]. Computers & Mathematics with Applications, 1988, 15(10): 887-896.
[10] 梁志文, 杨金民, 李元旗. 基于多项式模型和低风险的贝叶斯垃圾邮件过滤算法[J]. 中南大学学报(自然科学版), 2013, 44(7): 2787-2792.
LIANG Zhiwen, YANG Jinmin, LI Yuanqi. A Bayesian spam filtering algorithm based on polynomial model and low risk[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 2787-2792.
[11] 吴佳, 曾惟如, 陈瀚霖, 等. 基于隐马尔可夫模型的软件状态评估预测方法[J]. 软件学报, 2016, 27(12): 3208-3222.
WU Jia, ZENG Weiru, CHEN Hanlin, et al. Approach of measuring and predicting software system state based on hidden markov model[J]. Journal of Software, 2016, 27(12): 3208-3222.
[12] WANG Beiyang, WANG Lifeng. Analysis of defects propagation in software system based on weighted software networks[J]. Journal of Convergence Information Technology, 2012, 7(17): 63-77.
[13] 佟世文, 方建军, 李红星, 等. 一种基于线性模型预测的网络化预测模糊控制方法[J]. 中南大学学报(自然科学版), 2015, 46(4): 1281-1287.
TONG Shiwen, FANG Jianjun, LI Hongxing, et al. A networked predictive fuzzy control method based on linear model prediction[J]. Journal of Central South University (Science and Technology), 2015, 46(4): 1281-1287.
[14] REYES F, CERPA N, VEJAR A. The optimization of success probability for software projects using genetic algorithms[J]. Journal of Systems and Software, 2011, 84(5): 775-785.
[15] BONESS K, FINKELSTEIN A, HARRISON R. A lightweight technique for assessing risks in requirements analysis[J]. IET Software Journal, 2008, 2(1): 47-57.
[16] HALEY C B, LANEY R, MOFFETT J D. Security requirements engineering: a framework for representation and analysis[J]. IEEE Transactions on Software Engineering, 2008, 34(1): 133-152.
[17] WANG Chen, ONG Chongjin, SIM M. Model predictive control using segregated disturbance feedback[J]. IEEE Transactions on Automatic Control, 2010, 55(4): 831-840.
[18] 谢利子, 王青, 肖俊超. 风险驱动的软件项目缓冲分配方法[J]. 软件学报, 2010, 21(12): 3029-3041.
XIE Lizi, WANG Qing, XIAO Junchao. Reducing plan change: a risk driven software project buffer allocation method[J]. Journal of Software, 2010, 21(12): 3029-3041.
(编辑 陈灿华)
收稿日期:2015-05-03;修回日期:2015-07-22
基金项目(Foundation item):国家自然科学基金资助项目(61273232);教育部新世纪优秀人才支持计划项目(NCET-13-0785)(Project(61273232) supported by the National Natural Science Foundation of China; Project(NCET-13-0785) supported by Plan Program for New Century Excellent Talents in University)
通信作者:胡春华,教授,从事云计算、大数据分析等研究;E-mail:huchunhua777@163.com