混凝土泵车臂架实验台数值仿真和振动特性

任武^{1, 2}，吴运新^{1, 2}，滑广军^{1, 2}，张赵威^{1, 2}，曾谊晖^{1, 2}

(1. 中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083；

2. 中南大学 机电工程学院，湖南 长沙，410083)

摘要：针对泵车臂架末端运动轨迹确定和动力学求解困难的问题，建立泵车臂架实验台刚体模型；采用模态缩减技术对臂架柔性化，建立臂架系统的多柔体模型，然后利用虚拟弹簧阻尼法建立四节臂液压驱动油缸的等效模型，研究臂架系统臂、连杆、铰之间的运动学、动力学规律，对比分析臂架系统刚体模型、柔体模型和加液压油缸等效柔体模型的末端位移、液压缸运动受力以及整体臂架系统的第一阶固有频率。研究结果表明：臂架柔体模型运动停止后存在振动衰减的过程，其末端位移量比刚体模型增大数倍，柔性体液压缸关键部位的受力比刚体模型也大幅增加，第一节臂对整体末端振动位移的贡献最大，液压油缸的等效分析对固有频率值的影响较大。最后通过臂架实验台验证了建模和分析方法的正确性，为臂架系统低频振动抑制、轨迹规划和疲劳分析提供参考。

关键词：泵车臂架；多柔体；末端轨迹；振动；动力学

中图分类号：TU646          文献标志码：A         文章编号：1672-7207(2014)04-1065-06

Numerical simulation and vibration characteristics of boom system of concrete pump truck test rig

REN Wu^{1, 2}, WU Yunxin^{1, 2}, HUA Guangjun^{1, 2}, ZHANG Zhaowei^{1, 2}, ZENG Yihui^{1, 2}

(1. State Key Laboratory of High Performance Complex Manufacturing, Central South University, Changsha 410083, China;

2. School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

Abstract: In order to solve the problem of truck mounted concrete pump boom’s trajectory plan and dynamic calculation, a rigid model was established. Modal reduction technique was used to establish a flexible multi-body model. Virtual spring damper method was adopted to simulate the hydraulic cylinder actuator. The tip trajectory of the flexible booms, first natural frequency and force of hydraulic cylinder were analyzed. The results show that the flexible model has a vibration damping process and the tip displacement is several times larger than the rigid model. Besides the flexible model hydraulic cylinder force also increased. More over the first boom makes the largest contribution to the overall displacement and the equivalent hydraulic cylinder has significant influence on the natural frequency too. Finally an experiment is done on a boom test rig to validate the proposed approach above, which provides theoretical basis for the accurate vibration control, trajectory prediction and life assessment.

Key words: truck mounted concrete pump boom; flexible multi-body model; tip trajectory; vibration; dynamics

随着建设的发展和泵送高度、远度的需求，混凝土泵车臂架的长度也不断增加，中短臂架(垂直伸长量40 m以下)技术已日趋成熟，越来越向长臂架方向发展(垂直伸长量40 m以上)，特别是近年来出现了66，72，80，86和101 m的超长泵车臂架，臂架伸展时的大柔度、大变形非线性特征对泵车的影响越来越大，在泵送高度、距离不断增加，浇筑位置精准要求下，姿态变换时由于柔性变形引起的运动学变化、动力学响应必须加以考虑。臂架在运动过程中产生弹性剪切、扭曲变形，建立的运动学方程具有非线性、刚柔耦合特征^[1]。近年来国内外众多专家学者对多柔体动力学理论、混凝土泵车臂架系统的研究如下：张国忠等^[2-3]研究了某37 m泵车臂架的动态工况，得出整体结构的应力和变形，对浇筑过程自动化技术进行了探讨；陈凯等^[4]采用遗传模拟退火算法对混凝土泵车臂架系统进行优化，减小了各节油缸的行程和推力；王斌华等^[5-7]分析了混凝土泵车的冲击载荷响应，通过灵敏度分析得出了第一阶固有频率和质量对设计参数的影响，提出了一种减小整车振动的方法；Lenord等^[8]对多柔体非线性机液综合四节臂混凝土泵车模型进行了研究，建立了泵车臂架及其液压系统的3种模型并进行了对比分析，得出简化后符合实际工况的线性阻尼参数；郭岗等^[9]利用非线性理论对某44 m泵车臂架结构进行计算，对比了线性和非线性结果，为臂架设计提供了依据；戴丽等^[10-12]利用多柔体动力学对臂架系统进行建模和数值计算，并对末端浇筑进行了探讨；Cazzulani等^[13-14]建立了一个三节臂非线性多柔体臂架和泵送系统的综合实验台，通过模态观测法和扰动评估策略对液压装置进行控制，研究了柔性臂架末端振动的抑制和消减。现阶段泵车臂架的刚体建模分析比较成熟，但在探讨臂架柔性体的建模求解时和对油缸进行等效建模中，将油缸直接连接在两节臂间，这样造成臂架油缸受力分析准确度降低，另外部分研究中的振动分析是按照有线段方法进行，将刚体离散成若干弹簧连接的小刚体，实质上还是刚体分析方法。混凝土泵车主要由泵送系统和臂架系统组成，本文作者主要研究臂架系统柔性化后的运动学、动力学特性，依据多柔体运动学、动力学理论^[15]建立了混凝土泵车臂架的刚体模型，进一步利用模态缩减法^[16]和虚拟弹簧阻尼法将刚体模型转化为刚柔混合模型，分析柔性体模型和刚体模型的末端振动和第一阶固有频率影响因素，最后通过已有的臂架模型实验台证明了建立柔性模型的合理性和采用方法的正确性。

1  臂架多体系统模型的建立

1.1  虚拟弹簧阻尼法

混凝土泵车臂架由液压缸驱动，虚拟弹簧阻尼法是将液压缸等效成一定刚度和阻尼的模型^[17]，用于液压缸运动的控制，本文液压缸等效弹簧阻尼和臂架连接如图1所示。

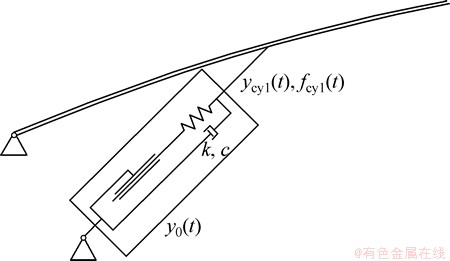
图1  液压缸和柔性臂物理模型

Fig. 1  Physical model of hydraulic cylinder

图1中液压缸受力F_cy1和运动位移y表达如下：

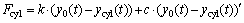   (1)

式中：y₀(t)为液压缸起始位置；y_cy1(t)为液压缸运动终止位置；t₀为初始时间；t为终止时间。仿真模型通过第1节液压缸的运动位移得出其受力。

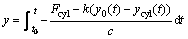        (2)

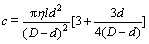          (3)

式中：c为液压缸阻尼；η为液压油运动黏度；l为活塞长度；d为活塞长度；D为油缸内径。依照文献[13]液压缸阻尼经验公式仿真中液压油缸阻尼c分别为1.08，0.90，0.20和0.02 N·s/mm；根据液压油和油缸并联串联计算出各节油缸的等效刚度k分别为40，30，20和6 kN/mm。

1.2  模态缩减法

模态缩减法通过有限元方法计算得到柔性体的模态^[18]，在FMBD(Finite element multi-body dynamics)理论前提下，通过模态振型叠加获得柔性体动态应力、应变和变形的一种方法，如图2所示。柔性体上任意一点i的三维坐标可以表示成：

        (4)

式中：A为方向余弦矩阵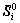；为点i未变形矢量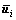；为相对变形量。点i的移动和转动模态矩阵表示为

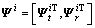              (5)

相对变形量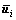采用模态坐标表示为

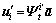                (6)

式中：是变形广义坐标，由式(4)和(6)得

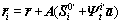           (7)

根据模态信息Ψ可以得出柔性体上某点的相应的速度和加速度方程，总体位移叠加关系由下式表示：

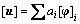              (8)

式中：[u]为各个节点的位移矢量和；a_i为模态参与因子；[φ]_i为构件的模态，通过各个节点的叠加得到柔性体的变形。

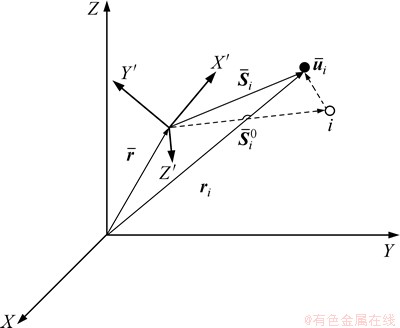
图2  柔性体模态坐标系

Fig. 2  Flexible body coordinate system

1.3  物理模型

本文建立臂架仿真研究时进行如下假设：

(1) 只考虑泵车臂架平面内变换姿态的运动特性，忽略泵车臂架左右扭转的影响，四节臂简化为欧拉-伯努利梁。

(2) 臂架、连杆、铰之间的连接用平动副、转动副和固定副模拟，其中液压油缸的运动用平动副等效。

(3) 在仿真过程中，臂架运动速度不能过大，以忽略运动中离心加速度和科氏加速度的影响。

依据以上假设，参照混凝土泵车臂架的实际结构，建立泵车臂架的刚体模型和刚柔混合模型，刚柔混合模型的拓扑结构如图3所示。

模型中的臂架、铰、连杆(弯板)数目和运动副类型如表1所示。

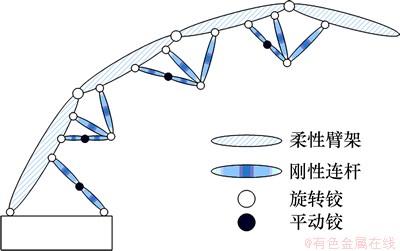
图3  臂架拓扑结构图

Fig. 3  Boom topology sketch

表1  臂架等效连接

Table 1  Equivalent connection of boom system

2  仿真分析和实验研究

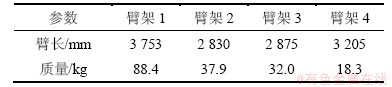
根据上文的理论和假设，在Recurdyn平台上建立泵车臂架实验台刚体模型，第1节臂固定在支座上，支座固定在可移动支架上，全刚体模型和各节臂的基本参数如表2所示。

表2  四节臂主要参数

Table 2  Main parameters of each boom

然后建立其刚柔混合模型，柔性臂架和刚性连杆的旋转副通过预先建立的刚性区域中节点连接，最后利用虚拟弹簧阻尼法把四节臂液压油缸等效为弹簧阻尼系统。建立好刚体模型、柔性体模型和加油缸弹簧阻尼的刚柔混合模型后，对典型的水平工况进行研究，主要分析3种模型运动应力、运动中油缸受力、末端位移的振动变化规律，旨在得出对实际工况有指导作用的运动学规律和动力学响应。

2.1  运动应力仿真分析

在Recurdyn中计算运动应力分布如图4所示。从图4可以得出：臂架水平向上运动中始终是第2和第3节臂架连接处应力处于最大值，并且随着运动停止后振动的衰减，其他各处的应力也作相应的增减变化，在操作速度允许的范围内，应力变化始终在臂架材料Q345B的许用应力230 MPa之内。

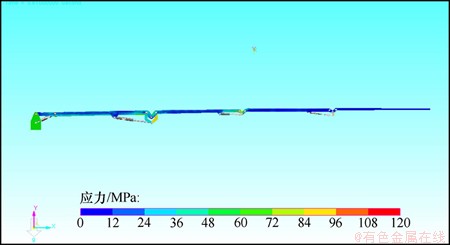
图4  柔性体运动应力云图

Fig. 4  Dynamics stress contour of flexible model

2.2  末端位移仿真研究

图5所示为3种模型末端位移。从图5可以看出：刚体模型末端位移在运动停止后立刻终止，而四节臂柔性化的刚柔混合模型的末端振动幅度达到0.3 m，伴随着振动的衰减逐渐停止，加弹簧阻尼等效的柔体模型的末端振动幅度达到0.7 m，衰减时间更长，充分表明振动的位移和部件柔性化的程度有关，随着部件的柔性数量增加，越来越能体现出臂架大范围运动的高柔性特征。

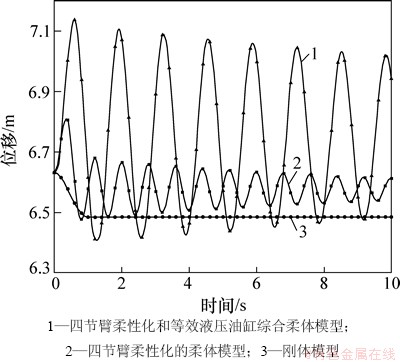
图5  3种模型末端位移

Fig. 5  Tip displacement of three models

2.3  油缸受力仿真研究

图6所示为3种模型液压油缸受力。从图6可以得出模型的受力变化规律：同一种模型中都是第2和第3节油缸受力较大，其次是第1节油缸，第4节油缸较小，刚体和柔体模型中都要将此部位作为重要设计优化目标；不同模型对比中，后2种柔性化后的模型在运动中比刚体模型相同部位受力均大幅增加，增幅约4.6×10⁴ N，因此，设计时就要充分考虑柔性体模型油缸受力。3种模型的液压油缸最大受力如表3所示。

2.4  实验研究和结果分析

为验证仿真分析结果，利用dewesoft多通道信号采集仪、三轴加速度传感器、倾角传感器、应变花等测试仪器和现有13 m臂架实验台进行实验，为了考察柔性影响最大范围特选定水平工况进行实验，在已有实验台上进行和仿真同样的条件下进行的，实验中通过操纵第1节臂的运动来获得相应的信号，通过末端加速度测试信号分析出系统的整体固有频率，末端加速度测试信号如图7所示。

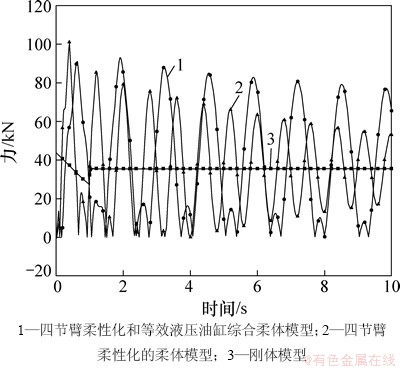
图6  3种模型液压油缸受力

Fig. 6  Hydraulic cylinder force of three models

表3  3种模型液压油缸最大受力对比

Table 3  Hydraulic cylinder maximum force comparison of three models           N

表4所示为仿真和实测最大应力。从表4可以看出：臂架应力的实测值与仿真值以及MSC/Nastran计算值比较接近，充分证明了仿真模型的正确性。

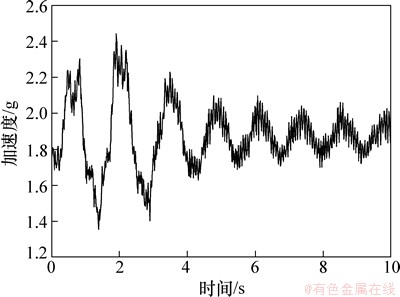
图7  臂架实验台末端加速度测试曲线

Fig. 7  Tip acceleration of boom test rig

表4  仿真和实测最大应力

Table 4  Maximum stress comparison between simulation and experiment

表5所示为仿真和实测末端最大位移。从表5可以看出：3种仿真模型和臂架实验台所测数据末端位移的差别，刚体模型末端位移由于运动停止后没有振动特性而较小约145 mm，四节臂架柔性化模型的位移与实测值比较接近，两者相差130 mm，加弹簧阻尼后柔性模型末端位移比实验值偏大250 mm，可能系油缸等效刚度计算误差导致整体臂架柔度偏大的结果。

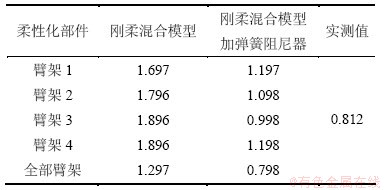
表6所示为柔性模型第一阶固有频率和实测值。从表6可以看出：不同柔性部位对整体臂架第一阶固有频率的影响，柔性化部件越多第一阶固有频率越低。当只有第1节臂柔性化时频率是1.697 Hz，分别只柔性化第2，3和4节臂后的频率逐步增大至约1.9 Hz，当四节臂全部柔性化后频率下降到约1.3 Hz；然后，在4节臂全部柔性化模型基础上首先仅加上第1节臂等效液压油缸弹簧阻尼，单独考察第1节油缸的影响，之后去掉第1节臂油缸等效弹簧阻尼，分别仅加上第2，3和4节臂等效液压油缸弹簧阻尼，单独考察不同液压油缸对整体频率的影响，最后4节臂全部加上等效液压油缸弹簧阻尼，所得频率如表6所示，其中四节臂全部柔性化再加上油缸弹簧阻尼综合模型的第一阶固有频率为0.798 Hz，与实际分析所得的0.812 Hz吻合较好；同时柔性化部件距离支座的远近也对整体频率的贡献也不同，第1节臂的柔性化对整体的影响最大，第2节臂次之，第3和第4节臂影响逐渐减小；另外，每节臂的等效弹簧阻尼对频率也有影响，本模型水平工况下第2和第3节油缸对频率影响较为明显。

表5 仿真和实测末端最大位移

Table. 5 Maximum tip displacement comparison between simulation and experiment          mm

表6  柔性模型第一阶固有频率和实测值

Table 6  First natural frequency between different models and experiment data              Hz

3  结论

(1) 建立了13 m四节臂泵车臂架实验台刚体模型，进一步利用模态缩减法建立其柔性体模型，最后采用弹簧阻尼法对四节臂液压油缸等效，建立了带液压油缸的柔性体模型，解决了液压缸运动等效问题。

(2) 实现臂架大规模柔性体的运动过程应力分析，对比臂架3种模型的运动学规律、动力学特性，分析了3种不同模型的油缸平动副受力、臂架末端位移和不同臂以及油缸弹簧阻尼对第一阶固有频率的影响，获得了与实际臂架结构相近的计算结果。

(3) 在已有实验台上进行了实验验证，与仿真结果吻合较好，说明了臂架柔性分析和液压油缸等效的必要性和正确性，为后续的振动控制和疲劳寿命分析提供了依据。

参考文献：

[1] 国家自然科学基金委员会工程与材料科学部. 机械工程学科发展战略报告(2011—2020)[M]. 北京: 科学出版社, 2010: 24-46.

National natural science foundation of engineering and materials science department. Mechanical engineering disciplines development strategy report (2011—2020)[M]. Beijing: Science Press, 2010: 24-46.

[2] 张国忠, 周淑文, 姜雪梅. 混凝土泵车臂架布料机构及其运动学仿真方法的研究[J]. 沈阳大学学报, 2004, 16(6): 27-31.

ZHANG Guozhong, ZHOU Shuwen, JIANG Xuemei. Computer simulation of placing system and kinematics of concrete pump truck[J]. Journal of Shenyang University, 2004, 16(6): 27-31.

[3] 郭立新, 陈长征, 张国忠, 等. 混凝土泵车布料机构水平工况的动态分析[J]. 振动与冲击, 1999,18(3): 79-82.

GUO Lixin, CHEN Changzheng, ZHANG Guozhong, et al. Dynamic analysis of level operating mode of placing boom of truck concrete pump[J]. Journal of Vibration and Shock, 1999, 18(3): 79-82.

[4] 陈凯, 孙国正. 混凝土泵车臂架结构的智能优化设计[J]. 武汉理工大学学报(交通科学与工程版), 2003,27(2): 244-246.

CHEN Kai, SUN Guozhong. Intelligent optimum design of boom frame of concrete pumping vehicle[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2003, 27(2): 244-246.

[5] 王斌华, 吕彭民. 混凝土泵车臂架系统振动机理的研究[J]. 振动与冲击, 2011, 30(9): 259-263.

WANG Binhua, L Pengmin. Vibration mechanism of arm system of concrete pump truck[J]. Journal of Vibration and Shock, 2011, 30(9): 259-263.

[6] 王海英. 水泥混凝土泵车振动性能与结构优化设计研究[D]. 西安: 长安大学工程机械学院, 2003: 53-59.

WANG Haiying. Study on the vibration characteristics and structural optimal design of the concrete pump truck[D]. Xi’an: Chang’an University. College of Mechanical Engineering, 2003: 53-59.

[7] 王斌华. 基于流固耦合理论的混凝土泵车动力响应与疲劳强度研究[D]. 西安: 长安大学工程机械学院, 2009: 50-54.

WANG Binhua. Research on dynamic response and fatigue strength of pump truck based on the fluid solid interaction theory[D]. Xi’an: Chang’an University. College of Mechanical Engineering, 2009: 50-54.

[8] Lenord O, Fang S, Franitza D, et al. Numerical linearisation method to efficiently optimise the oscillation damping of an interdisciplinary system model[J]. Multibody System Dynamics, 2003, 10(2): 201-217.

[9] 郭岗, 许辉. 混凝土泵车臂架结构的几何非线性计算[J]. 建筑机械, 2007, 27(3): 69-70, 73.

GUO Gang, XU Hui. Geometrical non-linear calculation for boom structure of truck concrete pump[J]. Construction Machinery, 2007, 27(3): 69-70, 73.

[10] 戴丽, 刘杰, 刘宇, 等. 基于多体动力学的混凝土泵车臂架的运动分析[J]. 东北大学学报(自然科学版), 2007, 28(10): 1469-1472.

DAI Li, LIU Jie, LIU Yu, et al. Kinematic analysis based on multi-body dynamics for placer jib of concrete pump truck[J]. Journal of Northeastern University(Natural Science), 2007, 28(10): 1469-1472.

[11] 戴丽. 基于柔性多体动力学的混凝土泵车臂架系统的建模与仿真[D]. 沈阳: 东北大学机械工程与自动化学院, 2008: 33-42.

DAI Li. Modeling and simulation of concrote pump truck arm system based on flexible multi body dynamics[D]. Shenyang: Northeastern University. School of Mechanical Engineering Automation, 2008: 33-42.

[12] 刘杰, 戴丽, 赵丽娟, 等. 混凝土泵车臂架柔性多体动力学建模与仿真[J]. 机械工程学报, 2007, 43(11): 131-135.

LIU Jie, DAI Li. ZHAO Lijuan, et al. Modeling and simulation of flexible multi-body dynamics of concrete pump truck arm[J]. Chinese Journal of Mechanical Engineering, 2007, 43(11): 131-135.

[13] Cazzulani G, Ghielmetti C, Giberti H, et al. A test rig and numerical model for investigating truck mounted concrete pumps[J]. Automation in Construction, 2011, 20(8): 1133-1142.

[14] Cazzulani G, Resta F, Ripamonti F. A Feedback and Feedforward Vibration Control for a Concrete Placing Boom[J]. Journal of Vibration and Acoustics, 2011, 133(5): 21-28.

[15] Shabana A A. Dynamics of multibody systems[M]. London: Cambridge University Press, 2005: 190-200.

[16] 焦晓娟, 张渭, 彭斌彬. RecurDyn 多体系统优化仿真技术[M]. 北京: 清华大学出版社, 2010: 239-269.

JIAO Xiaojuan, ZHANG Jiewei, PENG Binbin. RecurDyn multibody system simulation and optimization technology[M]. Beijing: Tsinghua University Press, 2010: 239-269.

[17] Nissing D. A vibration damped flexible robot: Identification and parameter optimization[C]//Proceedings of the American Control Conference. Chicago: IEEE Press, 2000: 1715-1719.

[18] Yoon J W, Park T W, Lee S H, et al. Synthetic analysis of flexible multibody system including a very flexible body[J]. Journal of Mechanical Science and Technology, 2009, 23(4): 942-945.

(编辑  杨幼平)

收稿日期：2013-05-26；修回日期：2013-07-12

基金项目：国家高技术研究发展计划(“863”计划)项目(2008AA042802)；湖南省自然科学基金资助项目(11JJ3059)；湖南省科技计划项目(2010GK3091)

通信作者：吴运新(1963-)，男，广东兴宁人，博士，教授，博士生导师，从事机械结构动力学、机电控制、冶金机械研究；电话：0731-88877840；E-mail：wuyunxin@csu.edu.cn