Trans. Nonferrous Met. Soc. China 28(2018) 319-327

Prediction of forming limit curve for pure titanium sheet

Young-Suk KIM¹, Bong-Hyun LEE², Seung-Han YANG¹

1. School of Mechanical Engineering, Kyungpook National University, Daegu 41566, Korea;

2. Daegu-Gyeongbuk Center, Korea Automotive Technology Institute, Daegu 43011, Korea

Received 4 January 2017; accepted 19 April 2017

Abstract: Commercially pure titanium (CP Ti) has been actively used in the plate heat exchanger due to its light weight, high specific strength, and excellent corrosion resistance. However, researches for the plastic deformation characteristics and press formability of the CP Ti sheet are not much in comparison with automotive steels and aluminum alloys. The mechanical properties and hardening behavior evaluated in stress-strain relation of the CP Ti sheet are clarified in relation with press formability. The flow curve denoting true stress-true strain relation for CP Ti sheet is fitted well by the Kim-Tuan hardening equation rather than Voce and Swift models. The forming limit curve (FLC) of CP Ti sheet as a criterion for press formability was experimentally evaluated by punch stretching test and analytically predicted via Hora’s modified maximum force criterion. The predicted FLC by adopting Kim-Tuan hardening model and appropriate yield function shows good correlation with the experimental results of punch stretching test.

Key words: Kim-Tuan hardening equation; Hora modified maximum force criterion; pure titanium sheet; forming limit curve

1 Introduction

Heat exchangers are devices that perform heat exchange between two heat transfer fluids separated by solid walls (tubes or plates) at different temperatures. There are various types of heat exchangers. Among them, plate heat exchanger (PHE) has been widely applied to almost all industrial fields such as food industry, chemical industry, power generation facility, and general industry. Titanium heat transfer plates, which are frequently used in PHE, are manufactured by hydraulic presses with various patterns of ridge and corrugation (washboard pattern, herringbone pattern, etc) in order to maximize the heat exchange area and to increase the strength and rigidity of the plate. Figure 1 shows a representative form of titanium PHE, where red arrow indicates the direction of high-temperature medium flow, and blue one indicates low-temperature medium flow direction.

As a PHE material, a stainless steel sheet is mainly used. However, Grade 1 commercially pure titanium (CP Ti), which is excellent in non-strength, corrosion resistance and high temperature strength and has no toxicity, is used in the corrosive environment. The CP TI is known to have high ductility and low strength due to its low carbon and iron content. Recently, efforts have been made to improve the press formability and processing technology while Grade 2 and 3 titanium sheets with high strength are adopted to improve the heat exchange efficiency [1].

The pure titanium sheet is an allotropic metal with a hexagonal closed packed (HCP) crystal structure at low temperature and a body-centered cubic (BCC) structure at 800 °C or higher. On the other hand, the CP Ti has a very limited plastic sag system, a low elastic modulus and strong in-plane anisotropy. Compared with ordinary steel, it is a material hard to press forming. It is also known that the plastic deformation of the titanium plate is mainly caused by twin deformation, and there is a strength differential (SD) effect that has a distinctly different stress-strain curve in tension and compression in the direction parallel to the rolling direction [2].

The purpose of this work is to obtain basic data on the press formability of pure titanium sheet, which is relatively few compared with automotive steel sheet or aluminum sheet. For this purpose, forming limit curve (FLC) was evaluated by tensile test and punch stretching test using spherical punch for pure titanium sheet. The accurate modeling of the true stress-strain relationship obtained from the tensile test results is the most basic data for the PHE press forming and the design of the forming tool using CAE (computer aided analysis). In this work, we proposed a work hardening model that can best fit the tensile test results of pure titanium sheet, and predicted the forming limit curve analytically using the proposed flow curve model and compared it with the punch stretching test results.

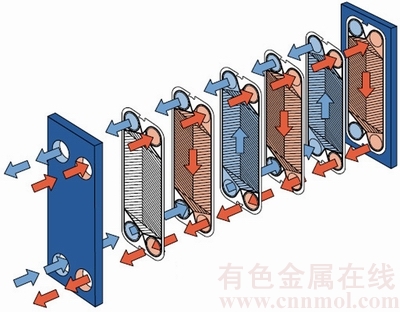
Fig. 1 Shape of titanium plate heat exchanger showing various pattern shapes

2 Experimental

2.1 Tensile test

Tensile specimens of ASTM E8 (equivalent to KS 0801 13B) were taken to evaluate the mechanical properties of pure titanium sheet for PHE with a thickness of 0.5 mm. This tensile specimen was subjected to a tensile test at a tensile rate of 1 mm/min according to the KS B 0802: 2003 test method. Table 1 gives the major chemical components, and Table 2 gives the tensile properties for the tensile tests along the 0°, 45° and 90° respected to the rolling direction. Figure 2 shows the tensile test specimens taken in transverse direction (TD) with tensile strains of 2.5%, 5%, 10%, 15% and 20%, respectively. Figure 3 shows the strain- engineering strain curve for each direction.

As known from Table 2 and Fig. 3, the pure titanium sheet has strong in-plane anisotropy. In other words, the yield stress (σ_y) and the anisotropy coefficient (R) of the pure titanium sheet increase significantly as the tensile axis rotates from the rolling direction to the transverse direction, whereas the elongation (δ) to the fracture decreases relatively.

On the other hand, as can be seen from the engineering stress-engineering strain diagram of Fig. 3, it can be seen that the nominal stress increases as the material is stretched in the 0° direction. However, in the case of the 45° and 90° direction, the stress gradually decreases with the deformation of the material after reaching the maximum load point. In the 0° direction, the occurrence of the local neck (marked as inverse triangular position in Fig. 3) begins at positions slightly past the maximum load point (strain of 0.37) and at 0.25 and 0.23 far beyond the maximum load point in the 45° and 90° directions, respectively.

Table 1 Main chemical components (mass fraction, %)

Table 2 Mechanical properties of pure titanium sheet

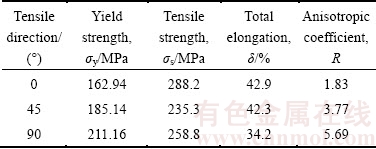
Fig. 2 Deformed shapes of TD specimens after various levels of tensile strain

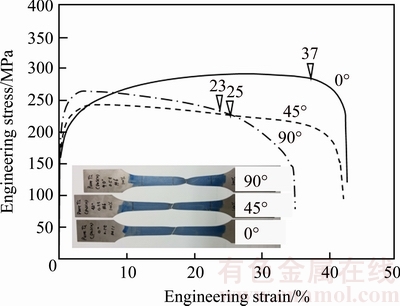
Fig. 3 Engineering stress-engineering strain curves of titanium sheet obtained from tensile tests

It is common that FCC sheet materials such as steel uniformly deform to the maximum load point and a neck occurs just beyond the maximum load point. In the case of the pure titanium HCP sheet in this work, it is seen that the necking is not observed even over the maximum load point in the 45° direction and the 90° direction, and the uniform stretching continues up to a considerable straining.

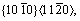
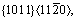
This special phenomenon is attributed to the different plastic deformation mechanisms in each direction in which the plastic deformation mechanism in the case of the CP Ti material is governed by the combination of the twin in the slip system of   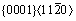 and the slip in the planes of (1012) and (1021) [3].

According to ISHIYAMA et al [3], the lower yield stress in the 0° direction is due to the fact that deformation twinning occurs more easily in this direction, which results in a lower initial yield strength but a further increase in twin boundaries. On the other hand, in the direction of 90°, the generation of twisted twin is relatively low, so that it shows low work hardening and low elongation.

Figure 4 shows the true stress-strain curve obtained from tensile tests at 0°, 45°, and 90°, and fitting results with a representative work hardening model. It is well established that level of predictive FLC is strongly depended on the applied hardening law [4]. As shown in Fig. 3, results of Swift and Voce model on capturing the flow curve of CP Ti sheet are unsatisfactory.

In this work, the work hardening model for representing new true stress-strain curve is proposed by combining the Swift model with the Voce model in the form of product (called Kim-Tuan model) [5]:

σ=σ_y+k(ε₀+ε)ⁿ[1-exp(-Bε)]                     (1)

where k, n, B and ε₀ are the material constants and σ_y and ε are the yield strength and plastic strain, respectively.

The Kim-Tuan equation can be easily reduced to the Swift equation when σ_y is omitted and B is infinity. Also, this equation can be simplified to the Voce equation when the value of parameter n is zero.

As indicated in Fig. 3, the engineering stress-strain diagram for a CP Ti sheet in rolling direction is obtained from a uniaxial tensile test. It is seen that the material is continuously deformed after the maximum tensile force is reached until the necking occurrence. Therefore, to get a reasonable extrapolation of flow curve after maximum uniform plastic strain of tensile test, the strain hardening model should give a correct prediction of work hardening rate or slope of flow curve at a certain stress-strain data point.

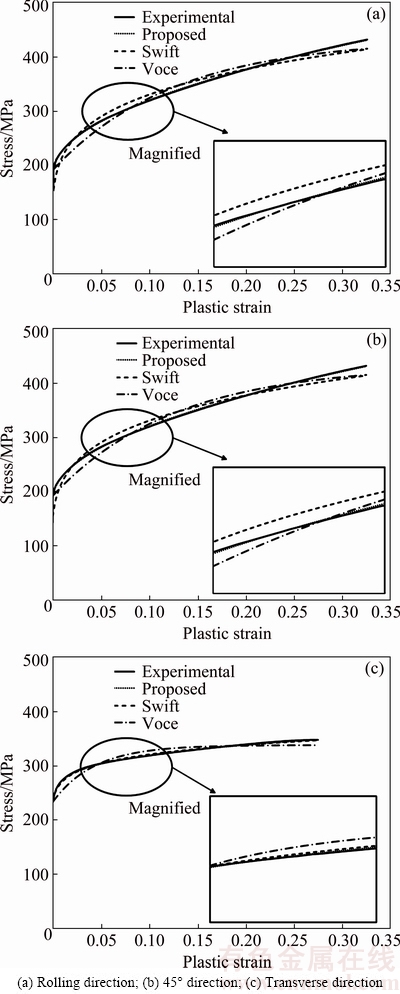
Fig. 4 Comparison between various hardening laws and experimental data obtained from tensile tests for titanium sheet

According to the Swift diffuse necking criterion, the condition for the maximum tensile force during the experiment can be expressed as

dF=d(Aσ)=dAσ+σdA=0                        (2)

This condition can be revised as

                            (3)

Hence, a value of the strain hardening rate can be implied analytically at the time when the maximum tensile force is reached. In the case of Kim-Tuan strain hardening model, the formulation of the strain hardening rate is as follows:

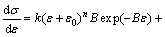
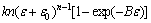                (4)

Let ε* and σ* denote the values of strain and stress at the time when the maximum tensile force is reached (here after called as maximum tensile force point or MTFP). Substituting this point into Eq. (3), we obtain:

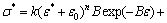
               (5)

Set R*=σ*-σ₀=k(ε*+ε₀)ⁿ[1-exp(-Bε*)], and then, Eq. (5) can be written as

             (6)

Dividing both sides of Eq. (6) for R*, we obtain:

             (7)

Simplifying this equation, we achieve the relation between parameter n and parameter B as

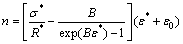                (8)

It was proven that value of parameter B is large enough to ignore the term B/[exp(Bε*)-1] in Eq. (8) by using two assumptions that all parameters are positive and strain hardening rate is a strictly decreasing function. Therefore, we obtain the equation:

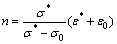                         (9)

From Eq. (9), it is clear that parameter n is an independent parameter whose value does not depend on the other parameter values. Thus, the value of parameters k and B in the Kim-Tuan model can be found using an optimization tool while the value of parameter n can be determined experimentally using Eq. (9).

Following Eq. (10) denotes the result of curve fitting of the model proposed in this work to the tensile test results in the 0° direction shown in Fig. 4.

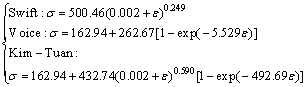              (10)

In order to secure the validity of the Kim-Tuan equation, the difference between the experimental value σ_exp and the predicted value σ_pre from each model is evaluated by the following equation:

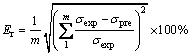             (11)

For the Swift model, Voce model and Kim-Tuan model, the errors are 2.34%, 2.16% and 0.21%, respectively, in the case of 0° direction, and 2.70%, 1.69% and 0.69%, respectively, in the case of 45° direction, and 2.00%, 0.47% and 0.18%, respectively, in the case of the 90° direction. In other words, it can be seen that the Kim-Tuan strain hardening model describes the experimental data more precisely because the error with the experimental values in all directions is as small as 1% or less.

2.2 Punch stretching test

Punch stretching tests with a spherical punch were carried out in accordance with ISO 12004 to measure the forming limit curve, which represents the forming limit at the time of press forming of sheet material. The forming limits of the pure titanium sheet were determined according to ASTM E2218-02 method [6] as follows. First, a dog-bone specimen with various widths of 2.0 mm square grid pattern is stretched under dry condition between specimen and punch until a specimen is fractured with a spherical punch of 102.5 mm in diameter in order to reproduce various deformation modes on the surface of stretched sheet. On the other hand, in order to reproduce the equi-biaxial stretch deformation of the sheet, a solid lubricant (SL-M2 Sentinel lubricant) and a polyurethane plate are inserted between the square specimen and the spherical punch. This assures the friction state in the punch stretching test to be in the frictionless state. Figure 5 shows the deformed shape of specimens after punch stretching test for determining forming limit curve. The fractures were observed at the apex of the dome in cases of uniaxial and biaxial tension specimens. Whereas, the fractures were observed near the specimen’s apex in other cases.

After the punch stretching tests, the deformed grid strain near the fracture site of each specimen was measured with a grid analyzer [7] to determine the forming limit curve judged by the boundary between the safe grid and the necked or fractures grid, as indicated in Fig. 6.

As can be seen in Table 2, because the pure titanium sheet has significantly anisotropic property, i.e., different mechanical properties in different directions, the forming limit curve is expected to vary depending on the testing direction of the specimen. In this work, the longitudinal direction of specimen to determine the forming limit curve was aligned parallel to the rolling direction.

Fig. 5 Deformed specimens of titanium sheet in punch stretching test to evaluate formability

Fig. 6 Magnified photos for fractured area of uniaxial tension (a), plane strain tension (b) and balanced biaxial tension (c) modes

Figure 6 shows photograph of grid deformation patterns of the fractured parts after tests under uniaxial tensile tension, plane strain tension, and equi-biaxial tension mode, respectively. The square grid was attached to measure the strain of the deformed grid.

Figure 7 shows the measured forming limit curve obtained from the punch stretching test on the minor and major strain coordinates. In the plane strain mode, the measured forming limit strain value is estimated to be about 0.36, which is slightly higher than the value of 0.32 measured by CHEN and CHIU [8] and lower than that measured by PORT et al [9]. It can be seen that there is no significant difference between these results in the uniaxial tension mode.

3 Results and discussion

As a method for predicting analytically the forming limit curve for a material that causes material fracture due to neck occurrence during tensile deformation, there are classical methods such as Swift’s diffusion neck theory, Hill’s local neck theory, and Marciniak-Kuczynski theorem, which assumes initial material defects [10].

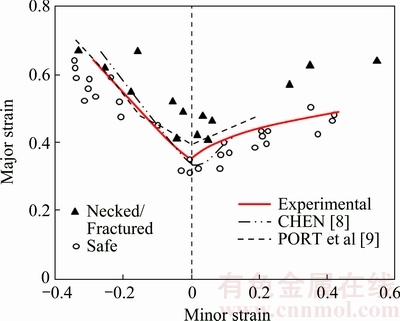
Fig. 7 Forming limit curves determined from punch stretching test

In this work, Hora’s modified maximum force criterion (MMFC) [11], which is easy to apply to various anisotropic yielding functions and is relatively simple to calculate, has been applied to the prediction of the forming limit curve of pure titanium sheet. In the maximum load condition, the fracture occurrence limit of the sheet is defined by the following equation:

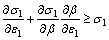                          (12)

where β(=dε₂/dε₁) is the strain ratio. In the application of Eq. (12), the yield criterion of the titanium sheet should be defined first.

CAO et al [12] reported that the Barlat '89 yield condition in the case of CP Ti sheet is equivalent or slightly improved compared to Hill’s 1948 yield criterion in predicting directional yield stress and anisotropy coefficient. COPPIETERS et al [13] studied the strain hardening characteristics after the necking of titanium sheet material and introduced the differential strain hardening model (DWH) taking different values of variable M, which determines the shape of the yield locus according to the plastic strain in the YLD2000-2d yield function. The result represents more closely the measured yield locus than the Hill’s 1948 yield function. In addition, ISHIKI et al [14] have shown that the existing anisotropic yielding functions could not well represent the experimental results showing severe in-plane anisotropy and asymmetry of yielding locus, and for this case yield function based on Bezier curve is more recommendable.

In this work, we use Logan-Hosford 1979 yield condition equation as yield condition of pure titanium sheet [15], which is known to be able to express the anisotropic yielding behavior of various sheet materials such as steel and aluminum in general:

F|σ₂-σ₃|^a+G|σ₃-σ₁|^a+H|σ₁-σ₂|^a=1                (13)

where F, G and H are material constants representing the anisotropy of the material and σ₁, σ₂ and σ₃ are the principal stresses in the directions of the principal anisotropy, respectively.

In this equation, F, G and H are determined from the definition of the anisotropy coefficient in the 0° and 90° directions, R₀ and R₉₀, as follows:

R₀|σ₂-σ₃|^a+R₉₀|σ₃-σ₁|^a+R₉₀R₀|σ₁-σ₂|^a=R₉₀(1+R₀)X^a    (14)

where X is the yield stress in the 0° direction and the index a is the parameter of the shape of the yield locus, which is generally known as 6 for BCC metal and 8-10 for FCC metal. On the other hand, the yield function for the case of a=2 in Eq. (14) agrees with Hill’s 1948 anisotropic yield function.

Figure 8 shows the yield locus measured when the equivalent plastic strain is ε=0.002 under various deformation modes such as uniaxial tension, plane strain tension, pure shear, and uniaxial compression of the laminate for the pure titanium sheet [10,16]. As can be seen, the yield locus of pure titanium sheet was assumed to be approximate to Hill’s 1948 anisotropic yield function. Thus, the forming limit curve was predicted using the exponent a=2 in Eq. (14) [16-18].

Fig. 8 Yield locus determined from various tests of pure titanium

Assuming a planar stress state in which the stress σ₃ in the thickness direction of the sheet is neglected in Eq. (14), the equivalent stress 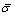 is defined by the following equation:

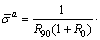
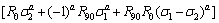      (15)

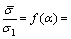
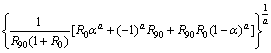   (16)

Therefore,

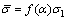                                (17)

where α(=σ₂/σ₁) is the stress ratio.

The equivalent strain is defined by the following equation from the principle of equivalent plastic work:

      (18)

The strain ratio β can be expressed in the function of stress ratio α by applying the Levy-Mises constitutive relation to the strain ratio as follows:

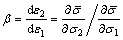                        (19)

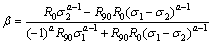
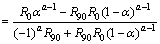              (20)

On the other hand, the strain hardening characteristics of the material can be expressed by the following equation:

                                  (21)

If Eqs. (15)-(20) are substituted into Eq. (12), the right side terms are expressed as follows:

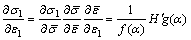              (22)

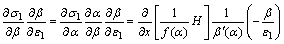      (23)

We assume here  In the above equation, .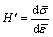

Therefore, Eq. (12) is finally expressed by the following equation:

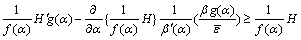        (24)

From this equation, the following equation is finally obtained:

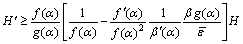      (25)

For a given strain ratio β in the range from -0.5 to 1.0, when the strains (ε₁)_n+1=(ε₁)_n+dε₁ and (ε₂)_n+1=(ε₂)_n+ dε₂ satisfy Eq. (25), the strain 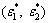 becomes the strain that defines the forming limit curve. Since Eq. (20) is a function of the stress ratio α, we need to numerically calculate the α for each β [17].

In Fig. 9, the experimentally determined forming limit curve is compared with the predicted results using the Swift model, Voce model, and Kim-Tuan model proposed in this work. From Fig. 9, it can be seen that the predicted forming limit strain values in the plane strain tension for both of Swift model and the Voce model are 0.24, which is estimated to be 0.12 lower than the experimental result (=0.36). On the other hand, the Kim-Tuan model is evaluated slightly higher in the equi-biaxial tension mode and slightly lower in the uniaxial tension mode compared with the experimental results, but almost well matches with the experimental value in the plane deformation mode.

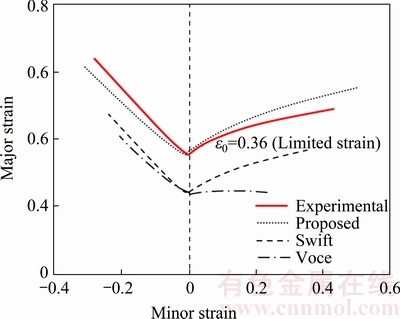
Fig. 9 Comparison between experimental forming limit curves and predicted forming limit curves using various hardening models

Figure 10 shows a comparison between flow curves and work hardening rate curves of CP Ti sheet based on different hardening laws. It is seen that the discrepancy of the work hardening rate curves is significant even while visualization of the difference from the flow curves is not much. It is well-known that predictive level of equivalent strain at diffuse neck strongly influences the instability of sheet metal [19]; therefore, this predicted strain influences FLC of sheet metal. From Fig. 10, Swift and Voce models generated a similar value of predicted diffuse necking strain meanwhile proposed hardening model increased this value for CP Ti sheet significantly. Moreover, predicted diffuse necking strain of Kim-Tuan model is close to the limited strain obtained from plane-strain specimen (ε₀). Therefore, both Swift and Voce models provided an underestimated value of ε₀ while proposed model yielded a correct prediction for ε₀.

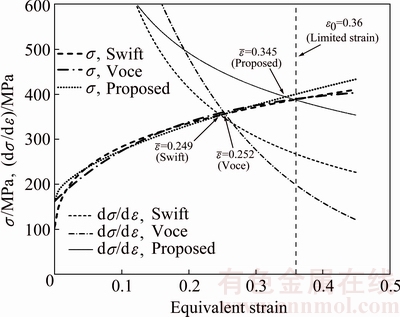
Fig. 10 Comparison between flow curves and work hardening rate curves based on different hardening laws

As can be seen from the fitting of the true stress- strain curve obtained in the uniaxial tensile test of Fig. 4, Kim-Tuan flow curve model fits the experimental data of stress-strain curve very well, so that Kim-Tuan flow curve model reflects well the strain hardening characteristic of the pure titanium sheet during plastic deformation and increases the accuracy of the prediction of forming limit curve. Therefore, it is necessary to introduce the model to better express the strain hardening characteristics of the material in predicting the forming limit of the material and simulating the plastic deformation process using CAE technology.

On the other hand, USUDA [20] showed that when the longitudinal direction of the test specimen was perpendicular to the rolling direction (as shown in this work), the forming limit strain value at plane strain mode (ε₀=0.34) is evaluated higher than when the longitudinal direction of the specimen was set to the rolling direction (ε₀=0.24). This may be induced from the fact that, as shown in Table 2, the anisotropy coefficient in the 90° direction was very high among the mechanical properties of the sheet.

For more precise prediction of the forming limit curve of the sheet material, it is necessary to introduce another anisotropic yield criterion which can describe well the yield locus and related plastic flow characteristic obtained through biaxial tensile tests. Even though the plasticity formulation for plastic flow is a little complicated, Cazacu-Barlat yielding function [21] and Barlat’s YLD2000-2d yielding function [22] may be better choices.

On the other hand, in this work, ASTM E2218-02 method is used, in which the contact between the plate and the spherical punch is performed in a non-lubricated state. However, in the case of adopting ISO 12004-2 method [23], in which a lubricating medium is inserted between the sheet material and the spherical punch and the experiment is carried out in the frictionless state, the forming limit curve in the equi-biaxial tension mode has a little higher value than that in the ASTM E2218-02 method [24]. Therefore, it is expected that the results of this work will better represent the results of the ISO 12004-2 method. This part will be left for further study.

4 Conclusions

1) As a result of the tensile test, it was found that the work-hardening Kim-Tuan model proposed in this work has the smallest error of 0.69% from the tensile test result of rolling specimen, thereby accurately describing the experimental data.

2) Hosford’s anisotropic yielding condition with a=2 and Kim-Tuan’s model were introduced into Hora’s modified maximum load condition to predict the forming limit line. As a result, the application of the Kim-Tuan model proposed in this work can well predict the forming limit curve obtained from the punch stretching test of the pure titanium sheet.

3) On the other hand, both of the Swift and Voce hardening model show lower level of the forming limit curve compared with the experimental results.

4) It is sure that the introduction of the appropriate model which expresses correctly the work hardening characteristics of the material is an important factor in predicting the forming limit of the material as well as CAE analysis of the plastic deformation process.

Acknowledgements

This work was supported by the National Research Foundation of Korea (NRF) granted by the Korea government [2014R1A2A2A01005903] and Priority Research Centers Program (2010-0020089), and a partial support from a grant [R0003356] (Tuning Professional Support Center in Daegu Metropolitan City) funded by the Ministry of Trade, Industry and Energy (MOTIE, Korea).

References

[1] FUJITA A, ITSUMI Y, NAKAMOTO T, YAMAMOTO K. Pre-coated titanium sheet with excellent press formability [J]. Kobelco Tech Review, 2011(30): 19-23.

[2] KUWABARA H, HORIUCHI H. Material modeling and evaluation of elastic-plastic behaviors of pure titanium subjected to bi-axial stress [C]//Proc Spring Conference 2007. Nagoya: The Japan Society for Technology of Plasticity, 2007: 165-166.

[3] ISHIYAMA S, HANADA S, IZUMI O. Orientation dependence of twining in commercially pure titanium [J]. The Japan Institute of Metals, 1990, 54: 976-994.

[4] WANG H B, WAN M, YAN Y. Effect of flow stress-strain relation on forming limit of 5754O aluminum alloy [J]. Transactions of Nonferrous Metals Society of China, 2012, 22(10): 2370-2378.

[5] PHAM Q T, KIM Y S. Identification of the plastic deformation characteristics of AL5052-O sheet based on the non-associated flow rule [J]. Metals and Materials International, 2017, 23(2): 254-263.

[6] ASTM E2218-02. Standard test method for determining forming limit curves [S]. Vo.l.03.01.

[7] SAFDARIAN R. Stress based forming limit diagram for formability characterization of 6061 aluminum [J]. Transactions of Nonferrous Metals Society of China, 2016, 26(9): 2433-2441.

[8] CHEN F K, CHIU K H. Stamping formability of pure titanium sheets [J]. Journal of Materials Processing Technology, 2005, 170(1-2): 181-186.

[9] PORT A L, TOUSSAINT F, ARRIEUX R. Finite element study and sensitive analysis of the deep-drawing formability of commercially pure titanium [J]. International Journal of Material Forming, 2009, 2: 121-129.

[10] EMMENS W C. Formability: A review of parameters and processes that control, limit or enhance the formability of sheet metal [M]. New York: Springer-Verlag Berlin Heidelberg, 2011.

[11] HORA P, TONG L, REISSNER J. Prediction methods for ductile sheet metal failure using FE-simulation [C]//Proc IDDRG. Lisboa, 1994: 363-375.

[12] CAO Q, ZHANG Q, ZHANG X. Anisotropy of mechanical behavior in commercially pure titanium sheets [J]. Journal of Harbin Institute of Technology, 2015, 22(1): 63-67.

[13] COPPIETERS S, YANAGA D, DENYS K, KUWABARA T. Identification of post-necking strain hardening behavior of pure titanium sheet [C]//Proc SEM 2015 Annual Conference. Society for Experimental Mechanics, 2015: 59-64.

[14] ISHIKI M, KUTABARA T, HAYASHIDA Y. Measurement and analysis of differential work hardening behavior of pure titanium sheet using spline function [J]. International Journal of Material Forming, 2011, 4: 193-204.

[15] LOGAN R W, HOSFORD W F. Upper-bound anisotropic yield locus calculations assuming <111>-pencil glide [J]. International Journal of Mechanical Sciences, 1980, 22: 419-430.

[16] KIM Y S. Formability analysis of pure Ti-sheet [R]. Internal Report of POSCO, 2015.

[17] KIM Y S, PARK J G. Review of formability and forming property for stainless steel [J]. Transactions of Materials Processing, 2011, 20(3): 193-205.

[18] PHAM Q T, KIM Y S. Evaluation of press formability of pure titanium sheets [J]. Key Engineering Materials, 2016, 716: 87-98.

[19] GHOSH A K. The influence of strain hardening and strain-rate sensitivity on sheet metal forming [J]. Journal of Engineering Materials and Technology, 1977, 99(3): 264-274.

[20] USUDA M. Press formability of commercially pure titanium sheets [J]. Nippon Steel Technical Report, 2002, 85(1): 24-30.

[21] CAZACU O, BARLAT F. Generalization of Drucker’s yield criterion to orthography [J]. Mathematics and Mechanics of Solids, 2011, 6(6): 613-630.

[22] BARLAT F, BREM J C, YOON J W, CHUNG K, DICK R E, LEGE D J, POURBOGHRAT F, CHOI S H, CHU E. Plane stress yield function for aluminum alloy sheets-Part 1: Theory [J]. International Journal of Plasticity, 2003, 19: 1297-1319.

[23] ISO 12004-2. Metallic material-sheet and strip-determination of forming limit curves-part 2: Determination of forming limit curves in the laboratory [S]. 2008.

[24] DILMEC M, HALKACHI H S, OZTURK F, TURKOZ M. Detailed investigation of forming limit determination standards for aluminum alloys [J]. Journal of Testing and Evaluation, 2013, 41(1): 10-21.

纯钛板成形极限曲线的预测

Young-Suk KIM¹, Bong-Hyun LEE², Seung-Han YANG¹

1. School of Mechanical Engineering, Kyungpook National University, Daegu 41566, Korea;

2. Daegu-Gyeongbuk Center, Korea Automotive Technology Institute, Daegu 43011, Korea

摘  要：商业纯钛(CP Ti)由于其轻质，高比强度和优异的耐腐蚀性能而被广泛应用于板式换热器。然而，与汽车用钢和铝合金相比，关于CP Ti板的塑性变形特征和压制成形性的研究相对较少。本文研究与CP Ti板压制成形相关的应力-应变关系及其力学性能和硬化行为。结果表明，CP Ti板的真应力-真应变关系曲线符合Kim-Tuan硬化方程，而不是Voce和 Swift模型。通过冲压试验验证CP Ti板的成形极限曲线(FLC)可作为压制成形性的标准，并可通过Hora改进的最大力准则来分析预测。通过Kim-Tuan硬化模型和合适的屈服函数预测的FLC与冲压试验的结果吻合良好。

关键词：Kim-Tuan硬化方程；Hora 改进的最大力准则；纯钛板；成形极限曲线

(Edited by Bing YANG)

Corresponding author: Young-Suk KIM; E-mail: caekim@knu.ac.kr

DOI: 10.1016/S1003-6326(18)64665-5