
Theoretical analysis of texture evolution in cold rolling process of
single crystal aluminum
L? Cheng(吕程)1, SI Liang-ying(司良英)1, 2,
ZHU Hong-tao(朱洪涛)1, LIU Xiang-hua(刘相华)2, K. TIEU1
1. School of Mechanical, Materials and Mechatronic Engineering, University of Wollongong,
Northfields Avenue, Wollongong NSW 2522, Australia;
2. State Key Laboratory of Rolling and Automation, Northeastern University, Shenyang 110004, China
Received 15 July 2007; accepted 10 September 2007
Abstract: The crystal plasticity finite element method(CPFEM), which incorporates the crystal plasticity constitutive law into the finite element method, was developed to investigate the rolling processes of the cubic oriented and Goss oriented Al single crystal. The simulation results show that after rolling the crystal predominantly rotates around the transverse direction(TD) for both orientations. The rotations around the rolling direction(RD) and the normal direction(ND) are negligible. The reduction plays a significant role in the texture evolution. The TD rotation angle increases with increasing reduction. The deformation bands exist in the rolled specimens with the cubic initial orientation. Compared with the cubic oriented specimens, the TD rotation angles in the Goss oriented specimens are very small.
Key words: crystal plasticity finite element method; texture evolution; rolling; single crystal aluminum
1 Introduction
The crystal orientation has a profound influence on the deformation behaviour, recrystallization behaviour and final properties of metals. During the rolling process, the crystal orientation is rotated relative to surroundings and the original orientation, which will lead to deformation bands and heterogeneous plastic flow. The cubic and rotated cubic orientations of FCC crystals are metastable under the rolling condition. They exhibit much more rotation than the stable orientations, such as Goss, copper and brass orientations. The rolling behaviour of the Al single crystal has attracted a significant interest in last decade.
Many researches have been conducted to experimentally investigate the rolling deformation behaviour of the Al single crystal[1-2]. It has been found that the crystal orientation mainly rotated about the transverse direction, namely the width direction in the flat rolling, and the crystal was subdivided into matrix bands and transition bands. There were usually four matrix bands along the thickness of the rolled specimens. The Taylor-type models have been applied to analyse the single crystal deformation[3-4]. These analyses indicated that the lattice rotation about the transverse direction was caused by the shear strain. However, the Taylor-type model could not accurately predict the rolling deformation behaviour of crystals due to its assumption of the uniform strain distribution. The detailed analysis of the microstructural evolution in the cold rolling process of Al single crystal has not been reported.
The crystal plasticity finite element method (CPFEM), which incorporates the crystal plasticity constitutive law into the finite element method, is in principle the best model for the simulation of plastic deformation of crystalline materials and for the prediction of deformation textures[5]. In this study, a CPFEM model is developed to investigate the rolling processes of the cubic oriented and Goss oriented Al single crystal. The predicted deformation behaviour is in good agreement with the experimental observations. The effects of reduction on the lattice rotation are discussed in detail.
2 Crystal plasticity theory
The crystalline material under load undergoes crystallographic slip due to dislocation motion on the active slip systems and elastic deformation including stretching and rotating of the crystal lattice[6-8].
The total deformation gradient(F) can be decomposed into two components as
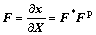 (1)
(1)
where X is the position of material points in the reference configuration and x is the position of material points in the deformed configuration; F* represents the elastic lattice deformation and F p describes the flow of material by slip.
A slip system α is specified by the slip direction vector s(α) and the normal vector to the slip plane m(α). They convert with the lattice when the lattice is stretched and rotated during the deformation. The slip direction vector s*(α) and the normal vector to the slip plane m*(α) in the deformed lattice are given by
s*(α)=F*?s(α) (2a)
m*(α)= m(α) ?F*-1 (2b)
where s(α) is the slip direction vector in the undeformed lattice, and m(α) is the normal vector to the slip plane in the undeformed lattice. The superscript -1 of F denotes the inverse.
The velocity gradient(L) is evaluated from the deformation gradient by
 (3a)
(3a)
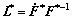 (3b)
(3b)
 (3c)
(3c)
where v is the velocity in the deformed configuration, 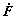 expresses a time derivative of F, L* is the contribution of the elastic and lattice rotation to L and Lp the plastic contribution.
expresses a time derivative of F, L* is the contribution of the elastic and lattice rotation to L and Lp the plastic contribution.
Because the plastic slip proceeds to the slip direction on the slip plane, Lp can be expressed by
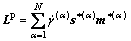 (6)
(6)
where 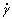 is the shear strain-rate caused by the plastic slip in the αth slip system and N the number of active slip system.
is the shear strain-rate caused by the plastic slip in the αth slip system and N the number of active slip system.
In this paper, the rate-dependent hardening model with the power law is employed, which relates the resolved shear stress (τ(α)) and the shear strain rate 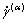 on a slip system α. The slip at a slip system also obeys the Schmid law, which states that slip begins when the resolved shear stress reaches a critical value.
on a slip system α. The slip at a slip system also obeys the Schmid law, which states that slip begins when the resolved shear stress reaches a critical value.
 for
for 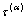 ≥
≥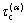 (18a)
(18a)
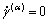 for
for 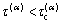 (18b)
(18b)
where 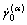 is the reference value of the shear strain rate, which is a constant for all the slip systems, n is the rate sensitive exponent. Both
is the reference value of the shear strain rate, which is a constant for all the slip systems, n is the rate sensitive exponent. Both 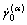 and n are the material parameters.
and n are the material parameters. 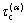 is the critical resolved shear stress of the slip system α.
is the critical resolved shear stress of the slip system α.
A linear hardening is assumed and the rate of change of the critical resolved shear stress is expressed as[9]
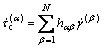 (19)
(19)
(20a)

 (20b)
(20b)
where hαβ is the instantaneous hardening moduli including the self hardening of each system (α = β) and latent hardening (α ≠ β), hαα is the self hardening moduli, q is a latent hardening parameter, γ0 is the reference value of slip, γ is the shear strain, τ0 is the initial critical resolved shear stress, τ1 is the breakthrough stress where large plastic flow initiates, h0 is the hardening modulus just after initial yield, hs is the hardening modulus during easy glide and fαβ represents the magnitude of the strength of a particular slip interaction between two slip systems α and β. The factors fαβ depend on the geometric relation between two slip systems. There are five constants for fαβ, namely a1(no junction), a2(Hirth lock), a3(coplanar junction), a4(glissile junction) and a5(sessile junction).
3 Simulation model
The finite element program ABAQUS/Standard has been widely used in the deformation and stress analysis of solids. It provides an interface whereby the users can write their own material constitutive model in a subroutine denoted user material subroutine(UMAT) in a very general way[10]. The major functions of UMAT are to provide the consistent tangent modulus (Jacobian matrix,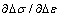 ) as required for an iterative Newton- Rhapson solution in ABAQUS, and to update stress and state variables including crystal orientation. In this paper the crystal plasticity constitutive model described in section 2 is implemented into ABAQUS/Standard by using UMAT.
) as required for an iterative Newton- Rhapson solution in ABAQUS, and to update stress and state variables including crystal orientation. In this paper the crystal plasticity constitutive model described in section 2 is implemented into ABAQUS/Standard by using UMAT.
The rolling process of single crystal aluminum was simulated. The simulation conditions were the same as those in LIU’s experiments[2]. Due to symmetry, only half specimen was modeled. The roll radius was 37.5 mm and the rotation speed of the roll was 25 r/min. The initial dimension of the specimen was 20 mm long and 1.45 mm high. The initial orientations of the specimen were exactly cubic and Goss. 4016 four-node plane strain elements were used to represent the specimen. The symmetric boundary conditions were applied to the mid-plane of the specimen. The reductions in thickness(ε) vary from 30% to 50%. The effects of two types of initial orientations, cubic orientation and Goss orientation, on the texture evolution have been investigated.
4 Results and discussion
To quantitatively determine the texture evolution, the misorientation of each node, which was calculated as related to the original orientation, was partitioned into three components which represent the rotations around the TD, RD and ND. The partition method proposed by WERT et al[1] was adopted in this study. The contour maps of crystallite rotation angle around the roll bite for the case of ε=30% and the coefficient of friction of 0.1 are shown in Fig.1. Figs.1(a)-(c) correspond to the rotation angles about the transverse direction(TD), rolling direction(RD) and normal direction(ND) respectively. The rotation angles about the TD, RD and ND are defined as θTD, θRD and θND respectively in the following. The roll bite region is marked at the top of Fig.1(a). It can be seen that θTD is much larger than θRD and θND. At the entry of the roll bite, θTD rotates to the positive angle. It increases rapidly along the RD, especially at the region near the specimen surface and θTD decreases from the surface of the specimen to the mid-plane of the specimen. At the top part of the roll bite in Fig.1(a), θTD increases along the RD to the positive maximum and then decreases. However at the bottom part of the roll bite, namely the region near the mid-plane of the specimen, θTD always increases along the RD. From the middle of the roll bite, the rotation angles at the top part and the bottom part have different signs: negative for the top part and positive for the bottom part. This sign difference remains in the rolled specimen, which indicates that there are two deformation bands parallel to the RD. Since the half of the specimen is displayed in Fig.1, the whole specimen should have four bands, which is consistent to LIU’s experimental observation[2]. Compared with θTD in Fig.1(a), θRD in Fig.1(b) and θND in Fig.1(c) are quite small. Therefore, the effect of reduction on θTD is only discussed in the following.
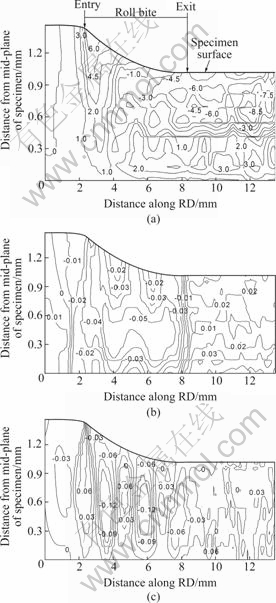
Fig.1 Contour maps of crystal rotation angles around TD (a), RD (b) and ND (c) for cubic orientation at ε=30%
The rotation angles around the TD for Goss orientation under the reduction of 30% are shown in Fig.2. Since both RD rotation angles and ND rotation angles have near-zero values within the entire region, they are not given in the figure. This indicates that the TD rotation also dominates for the Goss initial orientation. It can be seen from Fig.2 that θTD rapidly increases at the entry of the roll bite to the maximum values, and then decreases. After rolling the rotation angle around TD (θTD) are very small. The orientation has almost recovered to the initial Goss orientation for the cases of 30% reduction. Therefore, Goss orientation is often called the stable orientation.

Fig.2 Contour maps of crystal rotation angles around TD for Goss orientation at ε=30%
The crystal rotation angles around the TD (θTD) for the cubic orientation and Goss orientation at the reduction of 50% are shown in Fig.3. The distribution of θTD for 50% has a same pattern as ε = 30%. Comparing the results in Figs.1-3 shows that the reduction plays a significant role in the texture evolution. As the reduction
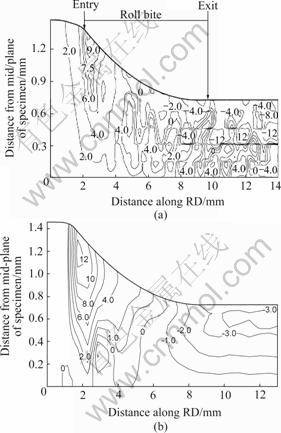
Fig.3 Contour maps of crystal rotation angles around TD for cubic orientation (a) and Goss orientation (b) at ε=50%
increases the rotation angles around the TD for both the cubic orientation and Goss orientation increase. However, the rotation angles in the latter are much smaller than those in the former. Deformation bands exist in the rolled specimen with the cubic orientation, while the texture is uniform in the rolled specimen with the Goss orientation.
5 Conclusions
1) The crystal plasticity finite element method (CPFEM), which incorporates the crystal plasticity constitutive law into the finite element method, was used to investigate the rolling processes of the cubic oriented and Goss oriented Al single crystal. The developed model is in good agreement with the experimental observation.
2) After rolling the crystal predominantly rotates around the TD for both orientations. The rotations around the RD and ND are negligible. The reduction plays a significant role in the texture evolution. The rotation angles around the TD increases with the reduction.
3) The deformation bands exist in the rolled specimens with the cubic initial orientation, while the texture is uniform in the rolled specimens with the Goss orientation.
References
[1] WERT J A, LIU Q, HANSEN N. Dislocation boundary formation in a cold-rolled cube-oriented Al single crystal [J]. Acta Mater, 1997, 45: 2565-2576.
[2] LIU Q, HANSEN N. Macroscopic and microscopic subdivision of a cold-rolled aluminium single crystal of cubic orientation [J]. Proc R Soc Lond A, 1998, 454: 2255-2592.
[3] LEE C S, DUGGAN B J. A simple theory for the development of inhomogeneous rolling textures [J]. Metall Trans A, 1991, 22: 2637-2643.
[4] LEE C S, DUGGAN B J, SMALLMAN R E. A theory of deformation banding in cold rolling [J]. Acta Metall Mater, 1993, 41: 2265-2270.
[5] WENK H R, VAN HOUTTE P. Texture and anisotropy [J]. Rep Prog Phys, 2004, 67: 1367-1428.
[6] BORG U. Strain gradient crystal plasticity effects on flow localization [J]. Int J Plast, 2007, 23: 1400-1416.
[7] KIWAKCZYK K, CAMBIN W. Model of plastic anisotropy evolution with texture-dependent yield surface [J]. Int J Plast, 2004, 20: 19-54.
[8] LU F, GUANG Z, ZHANG K S. Grain boundary effects on the inelastic deformation behavior of bicrystals [J]. Mater Sci Eng A, 2003, 361: 83-92.
[9] BASSANI J L, WU T Y. Latent hardening in single crystals (II): Analytical characterization and predictions [J]. Proc R Soc Lond A, 1991, 435: 21-41.
[10] ABAQUS Theory manual [M]. Version 6.6. ABAQUS Inc., 2006.
Corresponding author: L? Cheng; Tel: +61-2-42214639; E-mail: chenglu@uow.edu.au
(Edited by YUAN Sai-qian)