Horizontal trap-door investigation on face failure zone of shield tunneling in sands
来源期刊:中南大学学报(英文版)2021年第3期
论文作者:刘学彦 方宏远 王复明 袁大军
文章页码:866 - 881
Key words:face stability; trap-door test; lateral earth pressure; failure zone; soil arching; sand
Abstract: A novel horizontal trap-door test system was devised in this study to analyze the face stability of shield tunnels in sands. The test system can be used to investigate both the longitudinal and cross sections of the face failure simultaneously at one single apparatus and was employed to perform face stability tests on small-scaled tunnel models at single gravity. The lateral support pressures and failure zones were studied with varying sand materials and earth covers. The results demonstrate that the tunnel face moves back, the lateral active earth pressure on the tunnel face decreases rapidly to a residual value, and the lateral pressure distribution can be categorized into three stages during the failure process: 1) initial state; 2) pressure dissipation stage; and 3) pressure zone diminution stage. Furthermore, face failure firstly develops from a stable condition to the local failure state, and then continues to develop to the global failure state that can be divided into two sub-zones with different failure mechanisms: rotational failure zone (lower zone) and gravitational failure zone (upper zone). Further discussion shows that under the effects of soil arching, the shape of the gravitational failure zone can adopt arch shaped (most frequent) and column shaped (in shallow tunnels). Limit support pressure for face stability usually appears at δ/D=0.2%-0.5% (ratio of face displacement to tunnel diameter).
Cite this article as: LIU Xue-yan, FANG Hong-yuan, WANG Fu-ming, YUAN Da-jun. Horizontal trap-door investigation on face failure zone of shield tunneling in sands [J]. Journal of Central South University, 2021, 28(3): 866-881. DOI: https://doi.org/10.1007/s11771-021-4632-y.

J. Cent. South Univ. (2021) 28: 866-881
DOI: https://doi.org/10.1007/s11771-021-4632-y

LIU Xue-yan(刘学彦)1, FANG Hong-yuan(方宏远)2, WANG Fu-ming(王复明)2, YUAN Da-jun(袁大军)3
1. Department of Civil Engineering, Beijing Forestry University, Beijing 100083, China;
2. School of Water Conservancy and Environment, Zhengzhou University, Zhengzhou 450001, China;
3. Tunnel and Underground Engineering Research Center of Ministry of Education,Beijing Jiaotong University, Beijing 100044, China
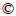 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: A novel horizontal trap-door test system was devised in this study to analyze the face stability of shield tunnels in sands. The test system can be used to investigate both the longitudinal and cross sections of the face failure simultaneously at one single apparatus and was employed to perform face stability tests on small-scaled tunnel models at single gravity. The lateral support pressures and failure zones were studied with varying sand materials and earth covers. The results demonstrate that the tunnel face moves back, the lateral active earth pressure on the tunnel face decreases rapidly to a residual value, and the lateral pressure distribution can be categorized into three stages during the failure process: 1) initial state; 2) pressure dissipation stage; and 3) pressure zone diminution stage. Furthermore, face failure firstly develops from a stable condition to the local failure state, and then continues to develop to the global failure state that can be divided into two sub-zones with different failure mechanisms: rotational failure zone (lower zone) and gravitational failure zone (upper zone). Further discussion shows that under the effects of soil arching, the shape of the gravitational failure zone can adopt arch shaped (most frequent) and column shaped (in shallow tunnels). Limit support pressure for face stability usually appears at δ/D=0.2%-0.5% (ratio of face displacement to tunnel diameter).
Key words: face stability; trap-door test; lateral earth pressure; failure zone; soil arching; sand
Cite this article as: LIU Xue-yan, FANG Hong-yuan, WANG Fu-ming, YUAN Da-jun. Horizontal trap-door investigation on face failure zone of shield tunneling in sands [J]. Journal of Central South University, 2021, 28(3): 866-881. DOI: https://doi.org/10.1007/s11771-021-4632-y.
1 Introduction
Shield machines (slurry or EPB shield) are widely used in tunnel construction for the development of subways system in cities. During shield excavation, sufficient support pressure must be prescribed to counteract water and earth pressure [1]. Otherwise, the tunnel face, particularly for shallow tunnels in sand, will become unstable or even collapse, threatening urban transportation systems and buildings [2, 3]. Thus, to ensure the construction safety of shield tunneling, face stability analysis is essential in revealing tunnel face failure mechanisms and predicting the limit support pressure.
Theoretical models for tunnel face stability have been developed, including the wedge-prism model [4-10], log-spiral model [11], multi-block model [12-18]. The failure zone of the wedge- prism model [19], as shown by the red line in Figure 1(a), is assumed as a sliding wedge loaded by a prism. The circular tunnel face is simplified as a rectangle with the same area, while it is assumed to be an ellipse with a smaller area in the multi-block model [13]. The sliding wedge of the multi-block model (shown by the blue line in Figure 1(a)) does not reach the crown of the tunnel as wedge-prism model, but instead turns back. The resulting failure zone thus shrinks as the failure surface climbs up to ground. The slip face of the log-spiral model [11] is assumed as a log-spiral shape, as shown in Figure 1(b). Soil arching is considered above the tunnel crown, and Terzaghi’s arching theory [20] is employed for the face stability analysis. However, it is only a two-dimensional model and cannot describe the failure zone fully. In contrast, the rotational failure model [21] is a three-dimensional model. Two log-spiral faces are employed, and the full circular tunnel face is considered in this model. Above all, the assumptions of slip surfaces or failure zones in these four theoretical models are different. As a result, the prediction results obtained with the four theoretical models are different. Therefore, the failure zones (or failure surfaces), which have not been unified by previous literatures, will be further investigated in this paper.
Physical model test plays an important role in face stability analysis. KIRSCH [22], IDINGER et al [23], BERTHOZ et al [24] investigated face failure mechanisms relying on longitudinal sections of the failure zone, whereas HAGIWARA et al [25] and LEE et al [26] studied failure mechanisms from the cross section of the failure zone. However, tests including both longitudinal and cross sections of the failure zone are rarely performed, and hence the full failure zone of the tunnel face fails to be revealed accurately. CHEN et al [27] performed a series of 3-D large-scale model tests on a tunnel with a diameter of 1 m, and a total of 48 earth pressure cells were installed in both the longitudinal and cross sectional directions to monitor the redistribution of the earth pressure during the failure process of tunnel face. The test delineated the boundaries of the soil-arching zone; however, observation windows were not installed, and thus neither the slip surfaces nor failure zone was observed. Because most of the available theoretical models rely on an assumption of the failure zones [5, 11, 13, 21, 28], it is of great significance to reveal the failure zone of a tunnel face from both the longitudinal and cross sections through tests.
In this study, horizontal trap-door tests were performed to extrapolate the failure zone during the process of face collapse. The tests were carried out with small-scale models at a single gravity. Both longitudinal and cross sections of the face failure zone were recorded simultaneously through two observation windows. The longitudinal section was modeled by a semi-cylinder with a semi-piston while the cross-section was simulated using a full cylinder with a piston. They were placed in one apparatus to allow the stress conditions to be controlled simultaneously. Both the failure zones and lateral earth pressure were investigated with a series of sand materials and earth covers. The failure mechanisms and support pressures of the tunnel face were also discussed.
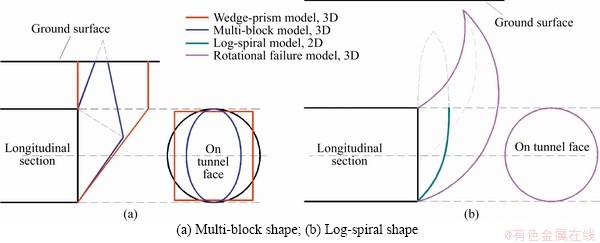
Figure 1 Four models for face stability analysis in previous literatures:
2 Test materials and experimental set up
2.1 Testing system and instrumentation
The horizontal trap-door method is employed for tests of the face stability during shield tunneling, as shown in Figure 2(a). Trap-doors are utilized in both Model A and Model B. Model A is intended to model the longitudinal-section of the tunnel while Model B is used to model the cross-section of the tunnel. The two model tunnels are placed within a single chamber, located at the same elevation (Figure 2(b)), and loaded using the same loading apparatus to ensure they are under the same stress environment. A coupling is installed connecting Models A and B to achieve synchronous movement of the model tunnel faces. Therefore, the observed soil displacements in the longitudinal and cross sections of the failure zones in front of the tunnel faces can represent the conditions for one tunnel. The failure zone can then be described and derived from the observed soil displacements.
The test system for Model A and Model B includes a chamber with internal dimensions of 1.0 m×1.5 m×1.5 m. Figures 2(a)-(c) show the location of Model A and Model B within the chamber. Model A is composed of a semi-tunnel model with a semi-cylinder and a semi-piston. The semi-piston, which plays the role of the tunnel face, is made of a steel semi-disk mounted on a horizontal steel rod. The semi-cylinder has an internal diameter of 300 mm and is installed close to the side wall at the corner of the chamber (as shown in Figure 2(c)). This wall is made of acrylic to allow for observation of the longitudinal displacement of soil layers in front of the tunnel face.

Figure 2 Layout of test system for face stability of shield tunnel:(Unit: mm)
Model B is composed of a model tunnel with a cylinder and a piston. Similarly, the piston playing a role of tunnel face is constructed of a steel disk mounted on a horizontal steel rod. The cylinder has the same diameter and is installed in the bottom center of the other acrylic wall (Figures 2(a)-(c)). The distance from the center of the cylinder to the parallel sidewalls is 750 mm, which is 2.5 times the tunnel diameter.
Model B is placed parallel to Model A, and Model A is pulled forward by 300 mm to avoid interaction between Model A and Model B. A coupling using manual lead screws ensures the models to move simultaneously. The displacement- controlled loading scheme can achieve a minimum loading step of less than 0.05 mm.
The stress environment of Models A and B is supplied by a loading plate. The loading plate is installed on the top wall of the chamber, which is reinforced with side ones composed of eight steel beam channels (Figure 2(a)). These eight steel beam channels are fixed on the rigid bottom plate. The two plates and eight steel beam channels are composed into the loading apparatus, as shown in Figure 2(a).
A scale with amplitude of 1 mm is printed on the two acrylic walls to indicate the amplitude of the soil displacements. A total of 37 pressure cells are uniformly installed on the tunnel face of Model B to measure the spatial distribution of the earth pressure, as shown in Figures 3(a) and (b). The total earth pressure can also be obtained from a force transducer installed behind the tunnel face. An additional four force transducers and a loading plate are installed on the loading apparatus. The force transducers and pressure cells are all channeled to an integrated instrument acquisition and computer analysis system.
2.2 Soil preparation and tests procedure
Fine sand and silty sand from Yellow River in China are used for the tests. The sands are sieved, washed and then oven dried to form a uniform ground. The grain size distributions of the fine sand and silty sand are presented in Figure 4, where Cu is the nonuniformity coefficient, Cc is the curvature coefficient, d50 is the particle size with cumulative distribution of 50%.

Figure 3 Pressure cells distributions on tunnel face in Model B:
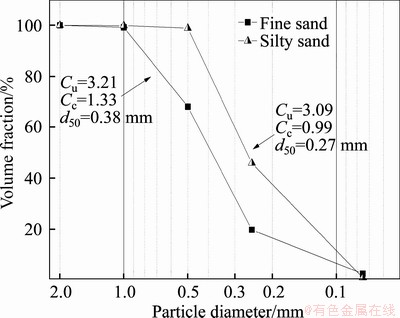
Figure 4 Grain size distributions of sands employed for tests
The average grain sizes of the fine sand and silty sand are 0.38 and 0.27 mm, respectively. Grains with a diameter less than 0.075 mm are removed through water washing. The specific gravity, bulk density, and void ratio of the fine sand are 2.56, 16.5×103 kN/m3 and 0.55, respectively, while those of the silty sand are 2.48, 16.0×103 kN/m3 and 0.55, respectively. Triaxial tests were carried out with the reconstituted sands to obtain shear strength parameters, as shown in Figures 5(a) and (b). From the triaxial tests and using Mohr-Coulomb criteria, the peak values of the friction angle and cohesion for the fine sand are 37.5° and 0 kPa, respectively, while those for the silty sand are 34.1° and 5.2 kPa, respectively.

Figure 5 Stress-strain relationships of triaxial tests for sands:
Tests are carried out with series of earth covers and varying sands. The test cases are summarized in Table 1. The stress environment of the model tunnels was achieved with the loading plate at 200 kPa. Using the prepared materials, each test is performed with the following procedures:
1) Sand dyeing. A portion of the sand is dyed using red ink and then dried to indicate layers in sand.
2) Ground formation. The ground is formed using the sand raining method. Thin, colored sand layers (approximately 10 mm thick, dyed with red ink) were placed at intervals of approximately 80 mm to observe the face failure development, as shown in Figure 6.
Table 1 Series of tunnel face stability tests



Figure 6 Sand ground formation
3) Initialization of the pressure cells and force transducer. The loading apparatus is slung up and the force transducer and pressure cells are initialized.
4) Installation of the loading apparatus. The loading plate and top wall are installed by fixing the top wall to side ones to ensure that it can resist the forces from the loading plate.
5) Modeling of the stress environment. A stress environment of 200 kPa for the sand ground is simulated through uniform pressure produced by the loading plate. The test loading pressure is measured and controlled by the force driving devices and transducer.
6) Model tests. Model tests are performed by moving the stiff disks backwards via rotation of the hand wheel. The stroke of the manual lead screws is set to be 0.3 mm/round. Thus, the stiff disks are moved back 0.05 mm through a 1/6 rotation of the hand wheel. An observation period of 3 min is used between two constitutive movements of the hand wheel to record measurements from the pressure cells and the soil displacements. This test process is repeated until the lateral pressure of the tunnel face decreases to a residual value. At this point, a total of 3 rotations of the hand wheel are carried out to observe the soil displacements, which represent the failure zone of the face collapse.
7) Replacement of the soil. The soil in the chamber is replaced with other soil materials for the next test.
Steps 2)-7) are then repeated until the tests are finished.
3 Experimental results
3.1 Earth pressure and distribution
3.1.1 Earth pressure
The lateral active earth pressures on the model tunnel face during its moving backward are recorded by pressure cells and a force transducer. Figure 7 shows the average lateral earth pressure versus the displacement of the tunnel face, δ, for silty sand and fine sand with cover-to-diameter ratios, C/D=0.5, 1.0. As the tunnel face moving back, the earth pressure drops sharply until the face displacement reaches 2.0 mm. Then, it diminishes to values of 1.2-4.6 kPa when the face displacement exceeds 10 mm. The lateral earth pressure varies not obviously with earth cover, as shown in Figure 8. Their small observed differences are irregular owing to the strength of sands and soil arching (it is discussed later in this paper).

Figure 7 Earth pressure versus drawing back displacement for series of sands and earth covers
3.1.2 Earth pressure distribution
The earth pressure distribution on the tunnel face is investigated using a total of 37 pressure cells (Figure 3). Figures 9 and 10 show the earth pressures along the vertical and horizontal center lines of the tunnel face with varying face displacements (the pressure cell at point A4 failed).
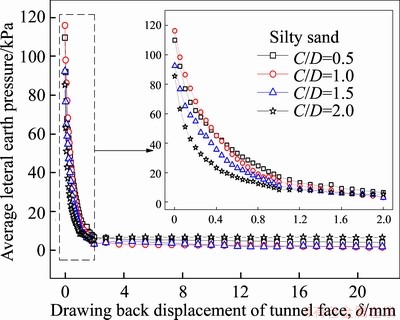
Figure 8 Earth pressure versus drawing back displacement for series of earth covers

Figure 9 Earth pressures in vertical center of tunnel face versus its displacement

Figure 10 Earth pressures in horizontal center of tunnel face versus its displacement
These results are from the test with silty sand at C/D=2.0. The earth pressures still decrease abruptly to residual values. However, the earth pressure on the center of the face decreases more slowly than those on the other locations as the face displacement exceeds 0.2 mm (as shown in Figures 9 and 10).
In the initial state, the earth pressure along the vertical center line of the tunnel face distributes irregularly, as shown in Figure 9. Point B4 exhibits the largest value owing to the surcharge. However, Point C4 does not exhibit the second largest value, which may be affected by soil arching. Even along the horizontal center line, the earth pressures still distribute non-uniformly because of non-uniform stress distribution of the sands [29, 30]. The stress environment and accuracy of the pressure cells also have some efforts on the differences of the earth pressures. As the tunnel face is drawn back, the earth pressures near the center decrease more slowly and are greater than those on the other locations, such as Points D3, D4, D5, and E4 shown in Figures 9 and 10.
The dissipation trend of the earth pressure distribution is also investigated by considering the full face pressure cells. Using Newton’s interpolation method, the earth pressure distribution can be obtained from the 37 pressure cells placed on the tunnel face. The earth pressure decreases to the residual values when the face displacement reaches 1.0 mm (as shown in Figures 7-10). Thus, face displacement levels of δ=0.0, 0.5 and 1.0 mm are chosen for further analysis.
Figure 11 shows the earth pressure distribution at face displacements of 0.0, 0.5 and 1.0 mm in silty sand with C/D=1.0. For δ=0.0 mm, the initial earth pressure field exhibits an irregular distribution with larger amplitudes near the side of the tunnel face (seen in Figure 11(a)); for δ=0.5 mm, the earth pressure decreases significantly from 180 to 40 kPa, particularly on the side of the tunnel face, as shown in Figure 11(b); for δ=1.0 mm, the earth pressure decreases to the residual values (in Figure 11(c)), and the residual amplitudes are mostly concentrated at the lower part of the tunnel face. For C/D=2.0, the initial earth pressure is distributed more non-uniformly (in Figure 12(a)). However, the same trend in the lateral earth pressure on the tunnel face can be still observed (Figures 12(a)-(c)). Variations in the lateral earth pressure field follow the similar trends, as summarized below.
1) Initial pressure state
The lateral active earth pressure is distributed irregularly on the tunnel face. Though, compared with the later stages of the tunnel face movement, it distributes more uniformly in general, which is close to the at-rest lateral pressure, as shown in Figure 13(a).

Figure 11 Earth pressure fields on tunnel face for different face displacements with C/D=1.0:
2) Sharp pressure decrease
The lateral pressure on the tunnel face decreases significantly with small displacements of the tunnel face (in the range of δ=0.0-0.5 mm), as shown in Figure 13(b). This appears especially on the side of tunnel face rather than in the center.
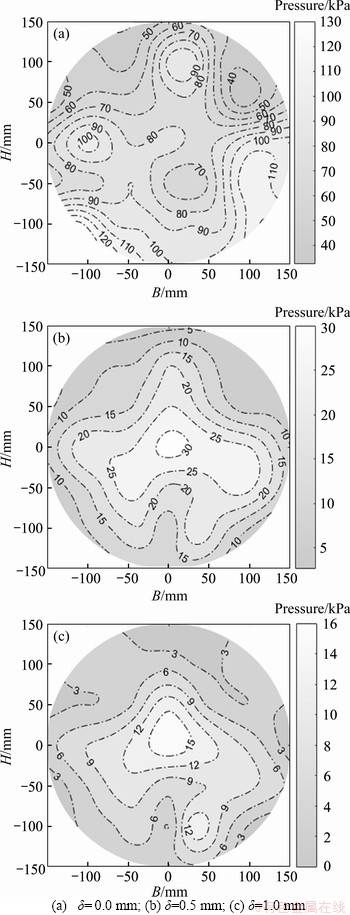
Figure 12 Earth pressure fields on tunnel face for different face displacements with C/D=2.0:
3) Pressure zone diminution
The lateral pressure on the tunnel face decreases further, with the pressure zone minified (in the range of δ=0.5-1.0 mm). The lateral pressure on the upper half of the tunnel face mostly dissipates as the displacement amplitude exceeds 1.0 mm, as shown in Figure 13(c).
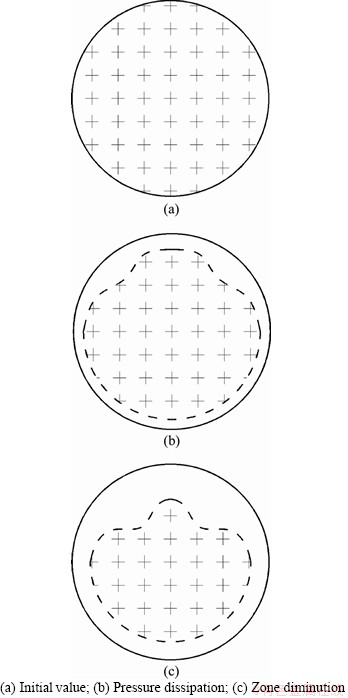
Figure 13 Trend of earth pressure distribution:
The earth pressure distribution on the tunnel face is similar to the earth pressure distribution on a vertical retaining wall. With displacement of the tunnel face, the active earth pressure will drop significantly to a residual value. With the limit displacement (δ=0.0-1.0 mm), the active earth pressure distributes mainly on the lower half part of the tunnel face, as presented in Figure 13.
3.2 Soil settlements and failure zone
Longitudinal and cross sections of the failure zone can be sketched using the colored layer lines [31-33] with the shear band depicted by the over-stretched regions of these lines [31]. Thus, colored layer lines were employed to investigate soil settlement, which indicates the face failure zone. Both longitudinal and cross sections of the tunnel were observed as tunnel face was drawn back. The soil settlements were recorded at face displacement intervals of 0.05 mm until the total displacement of 2.0 mm was reached. Then, soil settlements were recorded at face displacement intervals of 0.9 mm until a total displacement of 38.0 mm was reached. Figure 14 shows the soil settlements by dyed layers at three different face displacements. The dyed layers had a thickness of approximately 10 mm. However, the dyed layers were fully depicted only for face displacement level of 21.7 mm. For the other two face displacements, the thickness of the dyed layers was ignored and the middle height of the dyed layer was employed as a dyed line.
For the dyed lines shown in Figure 14, before the face displacement reached 2.9 mm, soil settlements were not visible, as indicated by the blue dashed lines in Figure 14. As face displacement reaches 12.7 mm, soil settlements can be described, as shown by the magenta dashed lines in Figure 14. When face displacement reached 21.7 mm, the soil settlements were obviously, as shown by the red dashed lines in Figure 14. Thus, soil settlements can be divided into three stages: 1) no visible displacement (δ/D=0.0%-1.0%), in which the soil layers exhibit no visible displacements; 2) local displacements (δ/D=1.0%- 4.2%), in which the soil settlements are distributed around the tunnel with small values (centimeter level); and 3) global displacements (δ/D>4.2%), in which soil displacements were clearly observed at a face displacement of 21.7 mm, and extend almost through the full stratum.
However, parts of the dyed lines were stable as the face displacement developed from 2.9 to 21.7 mm. Settlements only occurred in the soil ground located near the tunnel. The settlements of the dyed lines indicate the propagating zone of the face collapse. In addition, the dyed layers reveal additional details of this process. Portions of dyed lines are stretched thinner, which can be considered areas of shear failure. These portions of shear failure points can then be considered a slip face of the soil, as shown in Figure 14. The zone surrounded by the slip face is recognized as the failure zone of the soil layers. Therefore, failure zones occur simultaneously with soil settlements. Similar to the soil displacements, the failure process of tunnel face can also be divided into three stages:
1) Stable condition (δ/D=0.0%-1.0%). Soil layers remain in a stable condition without visible deformation or failures.
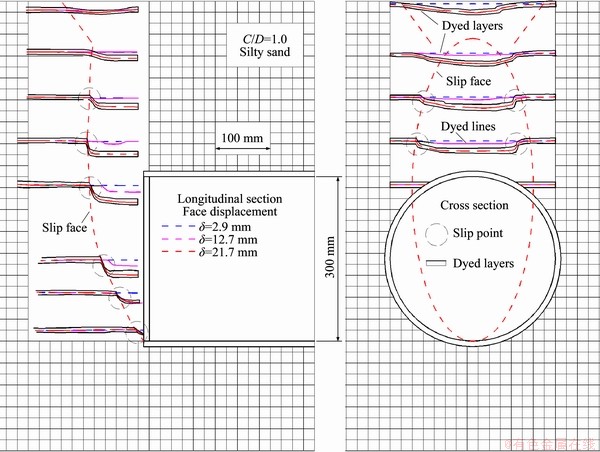
Figure 14 Settlement fields of slity sand with face displacement
2) Local failure (δ/D=1.0%-4.2%). The soil displacements around the tunnel have small amplitudes (in centimeter level). A slip surface forms at the tunnel face, which progressively propagates towards the ground surface (without necessarily reaching it). Local soil failure occurs.
3) Global failure (δ/D>4.2%). The soil displacement field extends almost through the full stratum and sometimes up to the ground face. The global failure occurs. The cross and longitudinal sections of the global failure zone can be described by an ellipse and a semi-ellipse, respectively (Figure 14).
Global failure zones were investigated with various earth covers and sand materials at a face displacement of 21.7 mm. Figure 15 shows the global failure zones of silty sand with varying cover-to-diameter ratios. The slip surface becomes slightly steeper and the failure zone becomes taller as cover-to-diameter ratio increases from 0.5 to 1.0 then to 1.5, respectively. However, the failure zone shrinks as earth cover-to-diameter ratio continues to increase from 1.5 to 2.0. This might suggest the formation of soil arching. Global failure zones for the silty sand and fine sand with C/D=1.0 are compared in Figure 16. The fine sand with greater shear strength exhibits a steeper slip face; while the global failure zone is narrower and the settlements extend to the ground. Thus, soil arching has not formed.
Comparing Figures 15 and 16, the longitudinal and cross sections of the failure zones for the two types of sand show the largest differences. However, the longitudinal sections of failure zones with different cover-to-diameter ratios are similar. Comparing Figures 14-16, the longitudinal-section of the failure zone resembles a chimney, and is approximately described by a semi-elliptical shape, while the cross-section of the failure zone can be fitted with an elliptical shape. The slip surface propagates upward away from the bottom of tunnel face until it reaches the crown of the tunnel, at which point it curves back as an arch on the tunnel and soil. However, soil arching may not always form, in which case, a funnel up to the ground forms (in Figures14 and 16). Thus, the shape of the failure zone can be summarized as two types: 1) a slip zone with an arching shape, and 2) a slip zone with a funnel shape, as shown in Figure 17.

Figure 15 Settlements fields of silty sand in series of earth covers
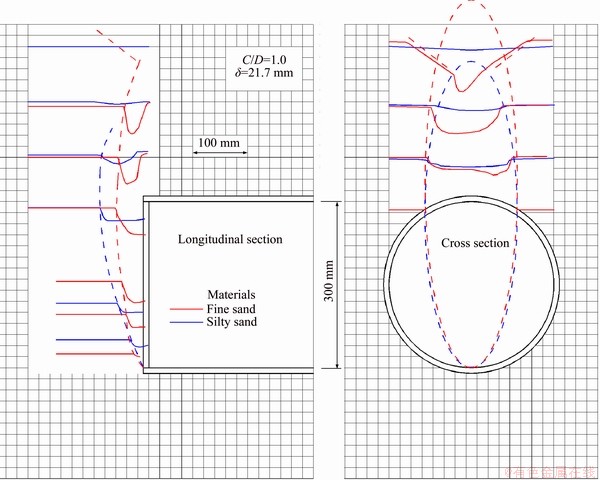
Figure 16 Settlements fields of fine sand and silty sand with C/D=1.0
4 Discussions
4.1 Soil arching
Trap-door tests [34, 35] suggest that the shape of the soil arching evolves from an initially curved shape to a triangular shape and eventually to a rectangular shape during inclusion settlement relative to the ground, as shown in Figure 18. This failure process can be also employed for the face stability analysis. Tunnel face stability has typically been investigated with horizontal trap-door tests [22, 26, 27]. During these tests, tunnel faces with insufficient supporting pressure are usually modeled with a trap-door moving back. However, the displacement of the tunnel face, which ranges from approximately about 5% to 10% of the diameter of the tunnel, is relatively small. Thus, the failure zone beneath the arch is typically a curved arching shape.

Figure 17 Longitudinal and cross profiles of global failure zone

Figure 18 Skech of arching mechanisms above a trap-door [34]
However, the value of C/D affects the shape of the arching [35]. A sufficient earth cover of the tunnel is necessary for the formation of soil arching. For deep tunnels, an arch and a small failure zone form near the tunnel crown; while for shallow tunnels, such as C/D<1.5, the arching affects a rectangular-shaped failure zone localized on the whole tunnel (shown in Figure 19).
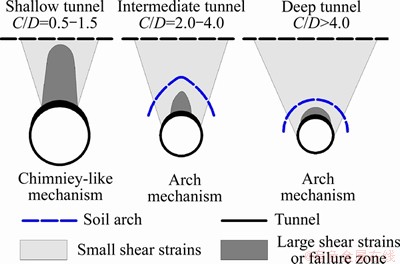
Figure 19 Skech of C/D effects on soil arching mechanism [35]
Thus, two types of failure zones result from the effect of soil arching: 1) an arch-shaped failure zone. Soil arching is a common phenomenon during tunnel excavation (Figure 20(a)), particularly in a sandy ground and was observed from the tests in this study, as shown in Figures 16-18; 2) a rectangular-shaped failure zone. Shallow tunnels (such as those with C/D<1.5) usually form rectangular shaped failure zones (Figure 20(b)).

Figure 20 Soil arching efforts on failure zone above tunnel crown:
Funnel-shaped failure zones were also observed in the tests in this study, as shown in Figures 15, 16 and 18.
4.2 Face failure mechanism
The colored layer lines can be employed to depict the failure zone. However, additional details of the failure zone have not been observed, such as the shear strains, shear bands/failures, and horizontal displacements of the soil. These parameters can be investigated using particle image velocity (PIV) [36] to describe the failure zone more clearly and accurately [35, 37].
However, the lateral sliding trend of the failure zone was described by MURAYAMA et al [11] and MOLLON et al [21] as a log-spiral shape, which induces a rotational failure mechanism. As log-spiral failure surfaces can satisfy the flow rule or normality condition [38], they are more critical in theoretical analyses. Usually, the log-spiral can be described as follows:
 (1)
(1)
where,
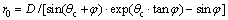 (2)
(2)
and φ is the friction angle of soil and θc=π/4-φ/2.
Thus, the shape of the failure zone can be determined from the tunnel diameter D and friction angle φ. The theoretical failure shape is compared with the experimental results for a tunnel face in silty sand, as shown in Figure 21, where O is the rotational center. The log-spiral failure shape is similar to the experimental failure shapes both in trend and magnitude. Thus, a rotational failure mechanism was detected in this study.

Figure 21 Log-spiral failure face vs experimental failure faces in silty sand
There is a rotational failure trend in the soil ahead of the tunnel face, and the failure zone ahead of the tunnel face surrounded by the failure surface exhibits a trend of lateral sliding. However, the failure zone above the tunnel crown does not have a rotation failure trend, but rather exhibits a gravity failure trend with soil arching, as shown in Figure 20. The failure zone of the tunnel face can thus be divided into two sub-zones with different failure mechanisms as follows:
1) Lower zone
The lower sub-zone forms mainly as a result of the insufficient support pressure. Soil within this zone has a tendency to rotate owing to the lateral earth pressure action on the soil and its gravity. Thus, the lower failure zone is primarily formed through shear failure, and there exists friction on the slip surface, as shown in Figures 22(a) and (b). The slip surface forms a lateral slip zone. This sub-zone can alternatively be termed as the rotational failure zone.
2) Upper zone
Typically, a vault forms above the rotational failure sub-zone owing to soil arching. There is no friction on the slip face of this zone, as shown in Figure 22(a). However, if the earth cover is thin, a rectangular-shaped collapse of the tunnel face may spread to the ground. This rectangular-shaped failure causes fiction on the slip face (seen in Figure 22(b)), which can be described by Terzaghi’s theory [20]. These two types of failure occur mainly due to soil gravity. This failure zone can be named as the gravitational failure zone.
These two sub-zones are developed with different failure mechanisms. However, they are in contact with each other through geometric and mechanical relationships. The geometric bottom of the upper sub-zone is primarily determined by the lower sub-zone, while the stability of the lower sub-zone is affected by the gravity of the upper sub-zone.
4.3 Critical state and limit support pressure
The horizontal trap-door was employed to investigate the collapse process of tunnel face in this study. The support pressure of the tunnel face, σc, is equal to the earth pressure acting on the tunnel face. Figure 23(a) shows the variation of normalized support pressure (ratio of σc to γD, where γ is the bulk density of sand) with normalized displacement (ratio of δ to D). In Figure 23(b), σc is normalized by the initial support pressure σc0 to evaluate the relative reduction of the initial support pressure.
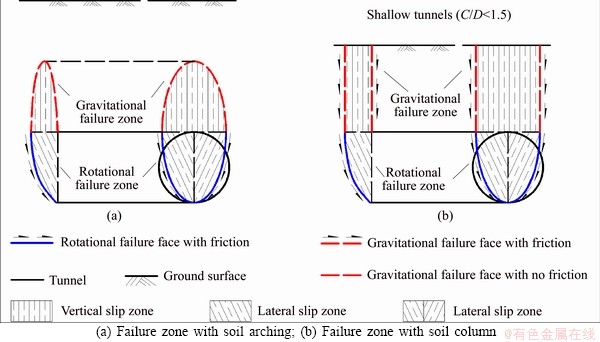
Figure 22 Failure mechanisms of circular tunnel face:

Figure 23 Normalized support pressure (a) and relative support pressure (b) with normalized drawing back displacement (normalized load-displacement curve)
The normalized/relative load-displacement curve decreases sharply just or at least partially due to soil arching, as shown in Figures 23(a) and (b). However, it decreases slowly or even increases at approximately δ/D=0.30%-0.50% for silty sand with C/D=0.5 and 1.0, respectively, which is referred to as the inflection point in this paper. This inflection point may suggest the critical state that the stable soil layers become unstable. The support pressure at inflection point could be regarded as the limit support pressure. For fine sand, inflection point appears at approximately δ/D=0.43%-0.50% for C/D=0.5 and 1.0, respectively.
The relative load-displacement curves are also compared with those from previous tests [22, 27], as shown in Figure 24. Inflection point appeared at approximately δ/D=0.20% in the tests carried out by CHEN et al [27], while about δ/D=0.50%- 0.53% for the tests performed by KIRSCH [22]. Thus, the limit support pressure usually appears at δ/D=0.20%-0.50%.

Figure 24 Comparisons of relative load-displacement curves between previous tests [22, 27] and tests in this work
5 Conclusions
This study has devised a novel test system for conducting face stability tests. With this system, both the longitudinal and cross sections of the face failure can be investigated simultaneously and observed with two separate observation windows in a single apparatus. The test system is used to perform face stability tests for a scaled tunnel model at a single gravity using horizontal trap-door method. Failure zones and lateral earth pressures (support pressures) are investigated using various sand materials, and earth covers. The conclusions drawn from this study are summarized below.
1) The lateral active earth pressure decreases abruptly to the residual value with increasing displacement of the tunnel face. The earth pressure at the center of the tunnel face center decreases more slowly than that at other locations. With increasing displacement of the tunnel face, the lateral pressure distribution field can be categorized into three failure process stages: the initial pressure state, which is closed to the at-rest lateral pressure conditions, with irregular earth pressure distribution; the abrupt pressure change stage, in which the lateral pressure decreases significantly with small displacements of the tunnel face; and the pressure zone diminution stage, in which the pressure zone decreases with decreasing lateral pressure.
2) As the tunnel face is moved back, the failure zone can be categorized into three stages: stable conditions (δ/D=0.0%-1.0%), in which the soil layers remain in an elastic condition without visible deformation or failure; the local failure state (δ/D=1.0%-4.2%), in which the soil displacements distributed around the tunnel have small amplitudes, and local soil failure occurs; and the global failure state (δ/D>4.2%), in which the soil displacement field expands through almost the full stratum, and global failure occurs.
3) The failure zone can be divided into two sub-zones with different failure mechanisms: the rotational failure zone (upper zone) and gravitational failure zone (lower zone). Under the effects of soil arching, two failure zone shapes are revealed: arch-shaped (most common) and column-shaped (in shallow tunnels).
Contributors
The research goals were developed by LIU Xue-yan, FANG Hong-yuan, WANG Fu-ming, and YUAN Da-jun. LIU Xue-yan provided the test data and analyzed the measured data. The initial draft of the manuscript was written by LIU Xue-yan and FANG Hong-yuan. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
LIU Xue-yan, FANG Hong-yuan, WANG Fu-ming, and YUAN Da-jun declare that they have no conflict of interest.
References
[1] BROERE W. On the face support of microtunnelling TBMs [J]. Tunn Undergr Space Technol, 2015, 46: 12-17. DOI: 10.1016/j.tust.2014.09.015.
[2] ITA-AITES W G. Settlements induced by tunneling in soft ground [J]. Tunn Undergr Space Technol, 2007, 22(2): 119-149. DOI: 10.1016/j.tust.2006.11.001.
[3] BROERE W, FESTA D. Correlation between the kinematics of a tunnel boring machine and the observed soil displacements [J]. Tunn Undergr Space Technol, 2017, 70: 125-147. DOI: 10.1016/j.tust.2017.07.014.
[4] HORN N. Horizontal earth pressure on the vertical surfaces of the tunnel tubes [C]// National Conference of Hungarian Civil Engineer Industry. Budapest, 1961: 1-16. (in German)
[5] ANAGNOSTOU G, KOVARI K. Face stability conditions with earth-pressure-balanced shields [J]. Tunn Undergr Space Technol, 1996, 11(2): 165-173. DOI: 10.1016/0886-7798(96) 00017-X.
[6] BROERE W. Tunnel face stability & new CPT applications [D]. Delft: Delft University of Technology, 2001.
[7] PERAZZELLI P, ANAGNOSTOU G. Stress analysis of reinforced tunnel faces and comparison with the limit equilibrium method [J]. Tunn Undergr Space Technol, 2013, 38: 87-98. DOI: 10.1016/j.tust.2013.05.008.
[8] PERAZZELLI P, LEONE T, ANAGNOSTOU G. Tunnel face stability under seepage flow conditions [J]. Tunn Undergr Space Technol, 2014, 43: 459-469. DOI: 10.1016/j.tust. 2014.03.001.
[9] ANAGNOSTOU G, PERAZZELLI P. Analysis method and design charts for bolt reinforcement of the tunnel face in cohesive-frictional soils [J]. Tunn Undergr Space Technol, 2015, 47: 162-181. DOI: 10.1016/j.tust.2014.10.007.
[10] LU X, ZHOU Y, HUANG M, LI F. Computation of the minimum limit support pressure for the shield tunnel face stability under seepage condition [J]. Int J Civ Eng, 2016, 1-15. DOI: 10.1007/s40999-016-0116-0.
[11] LIU X Y, WANG F M, FANG H Y, YUAN D J. Dual-failure-mechanism model for face stability analysis of shield tunneling in sands [J]. Tunnelling and Underground Space Technology, 2019, 85: 196-208. DOI: 10.1016/j.tust. 2018.12.003.
[12] DAVIS E H, GUNN M J, MAIR R J, SENEVIRATINE H N. The stability of shallow tunnels and underground openings in cohesive material [J]. Geotechnique, 1980, 30(4): 397-416. DOI:10.1680/geot.1980.30.4.397.
[13] LECA E, DORMIEUX L. Upper and lower bound solutions for the face stability of shallow circular tunnels in frictional material [J]. Geotechnique, 1990, 40(4): 581-606.
[14] TANG X W, LIU W, ALBERS B, SAVIDIS S. Upper bound analysis of tunnel face stability in layered soils [J]. Acta Geotech, 2014, 9(4): 661-671. DOI: 10.1007/s11440-013- 0256-1.
[15] ZHANG C, HAN K, ZHANG D. Face stability analysis of shallow circular tunnels in cohesive–frictional soils [J]. Tunn Undergr Space Technol, 2015, 50: 345-357. DOI: 10.1016/ j.tust.2015.08.007.
[16] HAN K, ZHANG C, ZHANG D. Upper-bound solutions for the face stability of a shield tunnel in multilayered cohesive–frictional soils [J]. Comput Geotech, 2016, 79: 1-9. DOI: 10.1016/j.compgeo.2016.05.018.
[17] KHEZRI N, MOHAMAD H, FATAHI B. Stability assessment of tunnel face in a layered soil using upper bound theorem of limit analysis [J]. Geomech Eng, 2016, 11(4): 471-492. DOI: 10.12989/gae.2016.11.4.471.
[18] HAN K H, ZHANG C P, LI W, GUO C X. Face stability analysis of shield tunnels in homogeneous soil overlaid by multilayered cohesive-frictional soils [J]. Math Probl Eng, 2016: Article ID 1378274, 1-9. DOI: 10.1155/2016/137 8274.
[19] ANAGNOSTOU G, KOVARI K. Face stability conditions with earth-pressure-balanced shields [J]. Tunn Undergr Space Technol, 1996, 11(2): 165-173. DOI: 10.1016/0886-7798(96) 00017-X.
[20] TERZAGHI K. Theoretical soil mechanics [M]. New York: Wiley, 1943. DOI: 10.1002/9780470172766.
[21] MOLLON G, DIAS D, SOUBRA A H. Rotational failure mechanisms for the face stability analysis of tunnels driven by a pressurized shield [J]. Int J Numer Anal Met, 2011, 35(12): 1363-1388. DOI: 10.1002/nag.962.
[22] KIRSCH A. Experimental investigation of the face stability of shallow tunnels in sand [J]. Acta Geotechnica, 2010, 5(1): 43-62. DOI: 10.1007/s11440-010-0110-7.
[23] IDINGER G, AKLIK P, WU W, BORJA R I. Centrifuge model test on the face stability of shallow tunnel [J]. Acta Geotech, 2011, 6(2): 105-117. DOI: 10.1007/s11440- 011-0139-2.
[24] BERTHOZ N, BRANQUE D, SUBRIN D. Face failure in homogeneous and stratified soft ground: Theoretical and experimental approaches on 1g EPBS reduced scale model [J]. Tunn Undergr Space Technol, 2012, 30(4): 25-37. DOI: 10.1016/j.tust.2012.01.005.
[25] HAGIWARA T, GRANT R J, CALVELLO M, TAYLOR R N. The effect of overlying strata on the distribution of ground movements induced by tunnelling in clay [J]. Soils Found (JSCE), 1999, 39(3): 63-73. DOI: 10.3208/ sandf.39.3_63.
[26] LEE C J, CHIANG K H, KUO C M. Ground movement and tunnel stability when tunneling in sandy ground [J]. J Chin Inst Eng, 2004, 27(7): 1021-1032. DOI: 10.1080/ 02533839.2004. 9670957.
[27] CHEN R P, LI J, KONG L G, TANG L J. Experimental study on face instability of shield tunnel in sand [J]. Tunn Undergr Space Technol, 2013, 33(1): 12-21. DOI: 10.1016/j.tust. 2012.08.001.
[28] ZHANG F, GAO Y, WU Y, WANG Z. Face stability analysis of large-diameter slurry shield-driven tunnels with linearly increasing undrained strength [J]. Tunn Undergr Space Technol, 2018, 78: 178-187. DOI: 10.1016/j.tust.2018. 04.018.
[29] MIURA K, MIURA S, TOKI S. Deformation behavior of anisotropic dense sand under principal stress axes rotation [J]. Soils Found (JSCE), 1986, 26(1): 36-52. DOI: 10.3208/ sandf1972.26.36.
[30] YANG Z X, LI X S, YANG J. Quantifying and modelling fabric anisotropy of granular soils [J]. Geotechnique, 2008, 58(4): 237-248. DOI: 10.1680/geot.2008.58.4.237.
[31] TANAKA T, SAKAI T. Progressive failure and scale effect of trap-door problems with granular materials [J]. Soils Found (JSCE), 1993, 33(1): 11-22. DOI: 10.3208/ sandf1972.33.11.
[32] CHAMBON P, CORTE J F. Shallow tunnels in cohesionless soil: Stability of tunnel face [J]. J Geotech (ASCE), 1994, 120(7): 1148-1165. DOI: 10.1061/(ASCE)0733-9410(1994) 120:7(1148).
[33] KAMATA H, MASHIMO H. Centrifuge model test of tunnel face reinforcement by bolting [J]. Tunn Undergr Space Technol, 2003, 18(2, 3): 205-212. DOI: 10.1016/S0886- 7798 (03)00029-4.
[34] IGLESIA G R, EINSTEIN H H, WHITMAN R V. Investigation of soil arching with centrifuge tests [J]. J Geotech Geoenviron, 2014, 140(2): 04013005. DOI: 10.1061/(ASCE)GT. 1943-5606.0000998.
[35] FRANZA A, MARSHALL A M, ZHOU B. Greenfield tunnelling in sands: The effects of soil density and relative depth [J]. Geotechnique, 2018. DOI: 10.1680/jgeot.17.P.091.
[36] WHITE D J, TAKE W A, BOLTON M D. Soil deformation measurement using particle image velocimetry (PIV) and photogrammetry [J]. Geotechnique, 2003, 53(7): 619-631. DOI: 10.1680/geot.53.7.619.37383.
[37] MARSHALL A M, FARRELL R, KLAR A, MAIR R. Tunnels in sands: The effect of size, depth and volume loss on greenfield displacements[J]. Geotechnique, 2012, 62(5): 385-399. DOI: 10. 1680 /geot.10.P.047.
[38] CHEN Wai-Fah. Limit analysis and soil plasticity [M]. Amsterdam: Elsevier, 2007.
(Edited by FANG Jing-hua)
中文导读
砂土地层盾构掘进面失稳区的水平活板门模型
摘要:本文设计了一种新型的水平活板门试验装置。该试验装置可以用于砂土地层盾构隧道开挖面稳定性分析。该试验系统可以同时研究工作面破坏的纵断面和横截面。本文使用该装置在单重力条件下对小型模型隧道进行了开挖面稳定性试验,研究了不同砂土材料和覆土厚度条件下的侧向土压力和破坏区域。结果表明,随着开挖面的向后移动,开挖面上的主动土压力迅速下降至残余值。同时在破坏过程中,侧向土压力分布可分为三个阶段:1)初始状态阶段;2)压力减小阶段;3)压力区减小阶段。此外,开挖面破坏首先从稳定状态发展到局部破坏状态,然后继续发展到整体破坏状态。整体破坏状态的失稳区域可分为旋转破坏区(下部区域)和重力破坏区域(上部区域)。这两个区域具有不同破坏机制。进一步讨论表明,在土拱效应下,重力破坏区的形状可分为拱形(最常见)和柱形(浅埋隧道)。开挖面稳定的极限支护压力一般出现在δ/D=0.2%~0.5%(掌子面位移与洞径之比)。
关键词:开挖面稳定性;活板门试验;侧向土压力;失稳区域;土压力;砂土
Foundation item: Project(51678037) supported by the National Natural Science Foundation of China; Project(2015CB057802) supported by the National Basic Research Program of China; Project(BLX2015-20) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2020-05-18; Accepted date: 2020-10-15
Corresponding author: LIU Xue-yan, PhD, Lecturer; Tel: +86-10-62336608; E-mail: happyhome-liu@163.com; ORCID: https://orcid.org/0000-0002-1493-8900; FANG Hong-yuan, PhD, Professor; E-mail: fanghongyuan@zzu. edu.cn

