Springback of thin-walled tube NC precision bending and its numerical simulation

GU Rui-jie(谷瑞杰), YANG He(杨 合), ZHAN Mei(詹 梅), LI Heng(李 恒)

College of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an 710072, China

Received 10 April 2006; accepted 25 April 2006

Abstract: The springback is one of the key factors which affect the forming quality of thin-walled tube NC precision bending. The elastic-plastic finite element method was proposed to study the springback process of thin-walled tube NC precision bending and the combination of dynamic explicit algorithm and the static implicit algorithm was proposed to solve the whole process of thin-walled tube NC precision bending. Then, the 3D elastic-plastic finite element model was established based on the DYNAFORM platform, and the model was verified to be reasonable. At last, the springback rule of thin-walled tube NC precision bending and the effect of geometry and material parameters on the springback rule of thin-walled tube NC precision bending were studied, which is useful to controlling the springback of thin-walled tube NC precision bending, and the numerical simulation method can be used to study other effect of parameters on the forming quality of thin-walled tube NC precision bending.

Key words: thin-walled tube; NC bending; precision forming; springback; simulation

1 Introduction

Thin-walled tube bending parts have been increasingly used in many industry fields, such as aviation, aerospace and automobile, for their easy satisfaction in light mass, high strength and low consuming. The numerical controlled(NC) rotary-draw tube bending technology (shown in Fig.1) not only enables the forming process of high technicalization, but also can satisfy the requirements of high precision, high efficiency, digitalization and intellectualization. So in aviation, aerospace and automobile industries, the cold NC tube bending process has been developed as one of the most important tube bending technologies[1, 2].

Some common defects, such as cracking, wrinkling, section distortion, wall thinning and springback, may be found during the thin-walled tube NC bending process, especially the tube bending process with small bend radius. Cracking and wrinkling should be avoided firstly, then the cross section distortion and wall thinning should be decreased as far as possible in the forming process [3,4]. After the forming process, the elastic deformation releases and the bent-tube is sprung back. The springback is one of the key factors which affect the forming quality of tube bending. When the value of the springback is beyond the error range, the accuracy of tube bending can not satisfy the requirement of applying. So it is necessary to study the spingback rule of thin-walled tube NC precision bending, by which the value of springback can be controlled effectively and the precision forming process of tube bending can be realized.

STELSON et al[5-9] have done a great deal of researches on the springback process of NC tube bending. In Ref.[5], by measuring the bending moment, the action center of pressure die and the friction force between mandrel and tube and the springback was predicted on line, and the predicting accuracy could reach 0.3?. STELSON et al[6] calculated the springback of tube bending with the springback theory of beam bending and the assumption I=0.7I₀ was used as the rotary inertia of

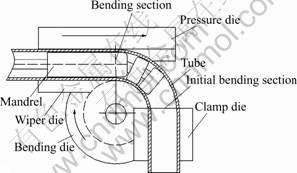
Fig.1 Sketch of NC tube bending

bent-tube. The analysis model was improved, in which an approximate expression in trigonometric form was introduced for the displacement field and the total deformation theory is employed as a constitutive relation[7]. The solution accuracy reached 25%. The method of bend-rebend was used to make the first bend to eliminate trial tubes, and the method of process control was developed to optimize the overall control strategy the overall tube error is minimized without increasing the accuracy of required hardware [8, 9]. STELSON has majored in the experiment and analysis of tube bending. His researches are very valuable to the production of tube bending. But his experiment are not comprehensive enough and his analysis is not accuracy enough because of so many assumptions. AL-QURESHI[10] analyzed the springback of tube bending, but his analysis was also not accuracy enough because of so many assumptions. There were some other researches on the forming process of NC tube bending[11-16], but these researches didn’t major in the springback.

By numerical simulation method, combined with theoretical analysis and experiment, the springback rule of thin-walled tube NC precision bending, the effect of geometry and material parameters on the springback rule of thin-walled tube NC precision bending were studied. This study is useful to controlling the springback of thin-

walled tube NC bending, and the method of numerical simulation can be used to study other effects of parameters on the forming quality of thin-walled NC tube precision bending.

2 Elastic-plastic finite element model of springback of thin-walled tube NC bending

The whole process of thin-walled tube NC precision bending includes three processes: tube bending, mandrel drawing and tube springback. The forming quality of tube bending are decided by the finally shape after these three processes. The processes of tube bending and mandrel drawing are dynamic, so the dynamic explicit algorithm is used to to solve the processes. And the process of tube springback is static, so the static implicit algorithm is used to to solve the processes. The whole process of thin-walled tube NC precision bending can be divided into two stages during simulating. The processes of tube bending and mandrel drawing are dealt with at the first stage, in which the bending operation and the mandrel drawing operation are realized by controlling the loading of dies. The process of tube springback is dealt with at the second stage. Because the calculator of DYNAFORM (LS-DYNA) can do not only dynamic explicit computing, but also static implicit computing, and it can realize the seamless transition between the two algorithms, so the software is chosen to establish the finite element model (as shown in Fig.2).

2.1 Establishment of finite element model

2.1.1 Establishment of geometry model

Because of the symmetry of the model, so only half of the model is established. Then the model is assigned to the symmetry constraint. When the geometry models of dies are established, only the contact surfaces between dies and the tube are needed. The structure of mandrel simplified reasonably is shown in Fig.3, then the mandrel

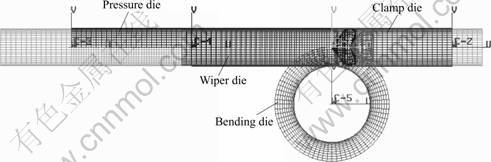
Fig.2 Elastic-plastic finite element model of springback of thin-walled tube NC bending

Fig.3 Schematic diagram of mandrel simplified reasonably

body and mandrel heads are linked to each other with CONSTRAINED_JOINT_SPHERICAL.

2.1.2 Dividing mesh

The mesh of the tube is established firstly, then the mesh of dies is gained by offsetting the mesh of the tube. In order to reflect the forming process, the mesh of the tube is refined in the field of big deformation (as shown in Fig.4).

Fig.4 Schematic diagram of mesh refining

2.1.3 Selection of element

There are four integral points in the plane of fully-integrated-shell-element. Not only the precision but also the computing efficiency are high to simulate thin-walled part forming with the element, so the element is used to dispose the tube, and five integral points are used along the thickness when thin-walled tube NC bending is simulated.

2.1.4 Selection of material model

The transversely anisotropic material model is used in the model. According to the Chinese Standard GB288-87, the experiment of material mechanical is done, by which Poisson ratio μ, transversely anisotropic exponent R and the stress-strain curve can be gained.

2.1.5 Treatment of contact

Penalty function method is used to treat the contact condition. The penalty stiffness coefficient is taken as 0.1. In order to accelerate the computing, only one-way search is done.

2.1.6 Treatment of friction

Coulomb friction model is used to compute the friction, in which friction is proportional to normal pressure. The mathematical expression of Coulomb friction model is shown as follows.

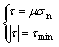
where  τ is equivalent shear stress; μ is friction coefficient; σ_n is equivalent normal stress; τ_min is ultimate shear stress.

2.1.7 Applying load

During the tube bending process, the clamp and the bending dies rotate, the pressure die boosts ahead, and the mandrel keeps stationary. When the process of tube bending is finished (t₀), the mandrel begins to be drawn back till the process is finished (t₁). The curves of bending velocity and the mandrel drawing velocity vs time are shown in Fig.5, in which the velocity is absolute value.

Fig.5 Curves of bending velocity and mandrel drawing velocity vs time

2.2 Simulation of springback

2.2.1 Constraint condition of springback computing

In order to keep the energy of springback computing unchangeable, whole the translation and rotary of bent-tube must be constrained. Constraints are applied on the end of the bent-tube because the end of the bent-tube deforms hardly (shown in Fig.6).

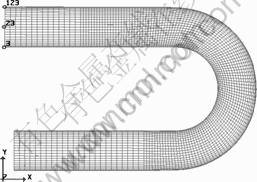
Fig.6 Constraint condition of springback computing

2.2.2 Determination of springback time

In order to determine reasonable springback time, different springback time can be applied. By comparing the computing result with different springback time, reasonable springback time can be gained.

2.2.3 Determination of springback steps

The whole springback process can be divided into several steps, so the springback of every step is small and the springback computing of every step can be controlled, which is useful to accelerate the convergence of spingback computing and increase the accuracy of springback computing.

2.2.4 Matrix update

Matrix update can be controlled. On the one hand, matrix can be controlled to update at every iteration, on the other hand, the limited times can be increased within every springback step.

2.3 Reasonableness evaluation of finite element model

The finite element model of thin-walled tube NC bending built in the paper has been verified with experiment. The experiment equipment is the W27YPC-63 full-automatic hydraulic pressure tube bender controlled by programmable logic controller (as shown in Fig.7). The principle of the tube bender is the same as NC tube bender, which has the NC function.

Fig.7 Diagram of W27YPC-63 tube bender

In the simulation of springback, the springback time is set as 4 s, the whole springback is divided into 4 steps and every step takes 1 s. In order to accelerate the convergence of spingback computing, matrix is controlled to update at every iteration and the limited times of iteration set as 200.

Fig.8 compares the results of simulation with experiment. The results of simulation and experiment agree with each other. The error ratio doesn’t exceed 18.57%. The finite element model is verified to be reasonable.

Fig.8 Simulation and experiment results of springback angle

3 Springback rule of thin-walled tube NC bending

The springback rules of 1Cr18Ni9Ti stainless steel tube and LF2M aluminum alloy tube NC bending with thickness 1mm, diameter 38mm and bending radius 57mm are studied with the finite element model established in the paper. The material parameters in the simulation are gained with the experiment of material mechanical.

Fig.9 shows the curve of bending angle vs springback angle of stainless steel tube bending. When the bending angle is small, the changing trend of springback angle with bending angle is nonlinear obviously, even that the springback angle changes very little within certain bending angle interval. It is because that the whole bent-tube includes the curved part and the transition part. When the bending angle is small, the springback of the transition part is more significant. When the bending angle is big, the springback angle changes linearly within the bending angle. It is because that the springback angle of the curved part changes linearly within the bending angle and that of the transition part keeps stable after the bending process is developed to steady forming.

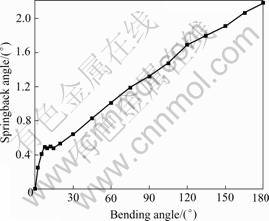
Fig.9 Curve of bending angle vs springback angle of stainless steel tube bending

Fig.10 shows the curve of bending angle vs springback angle of aluminum alloy tube bending. The change trend of springback angle within bending angle of aluminum alloy tube bending is similar to that of stainless steel tube bending. The difference is that the process of aluminum alloy tube bending is developed to steady forming early and the nonlinear change trend of springback angle with bending angle is not as obvious as that of stainless steel before steady forming.

When the bending angle is small, the springback of aluminum alloy tube bending is bigger than that of stainless steel tube bending. It is because that the yield strain of aluminum alloy is bigger, so the elastic deformation of the same whole deformation is bigger. When the bending angle is big, the springback of stainless steel tube bending is bigger than that of aluminum alloy tube bending. It is because that the strength factor of stainless steel is much bigger than that of aluminum alloy, so the stress of stainless steel tube bending is much bigger than that of aluminum alloy tube bending, and the elastic deformation of the same whole deformation is bigger.

Fig.10 Curve of bending angle vs springback angle of aluminum alloy tube bending

4 Effect of geometry on springback rule of thin-walled tube NC bending

The effect of geometry of tube bending includes relative bending radius and relative tube diameter, so the effects of relative bending radius and relative tube diameter on the springback are studied.

4.1 Effect of relative bending radius on springback rule

Fig.11 shows the curves of bending angle vs springback angle of stainless steel tube bending with thickness 1mm, diameter 38mm and relative bending radius 1.5, 2 and 2.5, respectively. When the bending angle is big, the bigger the bending radius is, the bigger the springback is. It is because that the length is bigger and more material takes part in the springback. When the bending angle is small, the bigger the bending radius is, the smaller the springback is, the more obscure the nonlinear changing trend of springback angle with bending angle is. It is because that the transition part of bent-tube is shorter and the process of tube bending is developed to steady forming early.

Fig.12 shows the curves of the bending angle vs springback angle of aluminum alloy tube bending with thickness 1mm, diameter 38mm and relative bending radius 1.5, 2 and 2.5, respectively. The springback rule of aluminum alloy tube bending and the effect of relative bending radius on the springback rule are similar to those of stainless steel tube bending.

Fig.11 Curves of bending angle vs springback angle of stainless steel tube bending with different relative bending radius

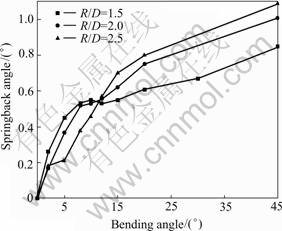
Fig.12 Curves of bending angle vs springback angle of aluminum alloy tube bending with different relative bending radius

4.2 Effect of relative tube diameter on springback rule

Fig.13 shows the curves of the bending angle vs springback angle of stainless steel tube bending with thickness 1mm, relative tube diameter 28, 38 and 50, respectively and relative bending radius 1.5. When the bending angle is big, the bigger the tube diameter is, the bigger the springback is. It is because that the length is bigger and more material takes part in the springback. When the bending angle is small, the bigger the tube diameter is, the smaller the springback is, the more obscure the nonlinear changing trend of springback angle with bending angle is. It is because that the rate of the elastic deformation in the same whole deformation is smaller.

Fig.14 shows the curves of bending angle vs springback angle of aluminum alloy tube bending with thickness 1mm, relative tube diameter 28, 38 and 50, respectively and relative bending radius 1.5. The springback rule of aluminum alloy tube bending and the effect of relative tube diameter on the springback rule are similar to those of stainless steel tube bending.

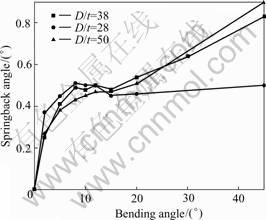
Fig.13 Curves of bending angle vs springback angle of stainless steel tube bending with different relative tube diameter

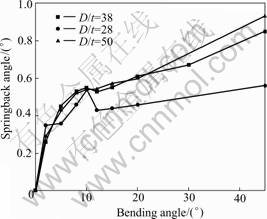
Fig.14 Curves of bending angle vs springback angle of aluminum alloy tube bending with different relative tube diameter

5 Effect of material parameters on springback rule of thin-walled tube NC bending

The effect of material parameters on the springback rule of thin-walled tube NC bending is studied with the finite element model established in the paper. The material parameters are set based on the material parameters values of 1Cr18Ni9Ti stainless steel tube gained in the experiment.

5.1 Effect of material parameters on springback rule

In order to study the effect of each material parameter on the springback rule of thin-walled tube NC bending, different values of material parameters are set to compute the springback.

5.1.1 Elastic modulus’ effect on springback rule

Fig.15 shows the curves of bending angle vs springback angle of tube bending with different elastic modulus (E). The bigger the elastic modulus is, the smaller the springback is, the more obscure the nonlinear changing trend of springback angle with bending angle is before steady forming. It is because that the rate of the elastic deformation in the same whole deformation is smaller and the bending process is developed to steady forming early.

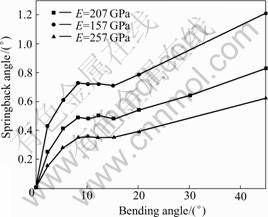
Fig.15 Curves of ending angle vs springback angle of tube bending with different elastic modulus

5.1.2 Effect of yield stress on springback rule

Fig.16 shows the curves of the bending angle vs springback angle of tube bending with different yield stress (σ_s). The bigger the yield stress is, the bigger the springback is, the more obvious the nonlinear changing trend of springback angle with bending angle is before steady forming. It is because that the stress with the same strain is bigger, the rate of the elastic deformation in the same whole deformation is bigger, and the bending process is developed to steady forming lately.

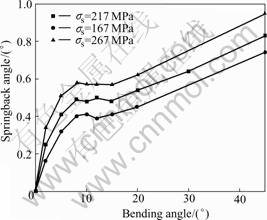
Fig.16 Curves of bending angle vs springback angle of tube bending with different yield stress

5.1.3 Effect of strength factor on springback rule

Fig.17 shows the curves of bending angle vs springback angle of tube bending with different strength factor (K). The bigger the strength factor is, the bigger the springback with the same bending angle is, and the more obvious the nonlinear changing trend of springback angle with bending angle is before steady forming. It is because that the stress with the same strain is bigger, so the elastic deformation with the same elastic modulus is bigger.

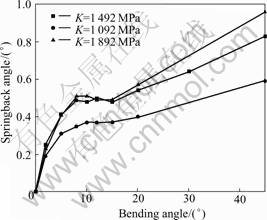
Fig.17 Curves of bending angle vs springback angle of tube bending with different strength factor

5.1.4 Effect of hardenability value on springback rule

Fig.18 shows the curves of bending angle vs springback angle of tube bending with different hardenability value (n). The bigger the hardenability value is, the smaller the springback is, and the more obscure the nonlinear changing trend of springback angle with bending angle is before steady forming. It is because that the stress with the same strain is smaller when the strain is smaller than 1, so the elastic deformation with the same elastic modulus is smaller.

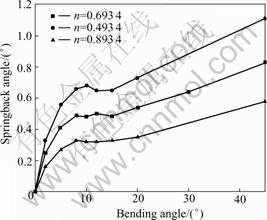
Fig.18 Curves of bending angle vs springback angle of tube bending with different hardenability value

5.2 Effect of significance analysis of material parameters on springback of thin-walled tube NC bending

In order to analyse the significance of effect of different material parameter on the springback of thin-walled tube NC bending, the changing rate of springback angle with each material parameter when the bending angle computed is 180?. The computing equation is as follows.

where  m₀, m₁ and m₂ are the experiment value, minimum and maximum of certain material parameter, respectively; Δθ₁ and Δθ₂ are the  springback angle when the material parameter is set as m₁ and m₂, respectively.

Table 1 shows the computing data, where d(Δθ) is the changing rate of springback angle with each material parameter. The significance of effect of different material parameter on the springback of thin-walled tube NC bending can be found in the Table 1. The significance of effect of these four parameters from elastic modulus E, strength factor K, hardenability value n to yield stress σ_s become weaker and weaker.

Table 1 Computing data of changing rate of springback angle with each material parameter

1) When the bending angle is small, the changing trend of springback angle with bending angle is nonlinear. After the bending process is developed to steady forming, the changing trend of springback angle with bending angle is totally linear. Aluminum alloy tube bending is more early developed to steady forming than stainless steel tube bending, and the nonlinear changing trend of springback angle with bending angle of stainless steel tube is more obvious than that of aluminum alloy tube before steady forming.

2) The smaller the bending radius and tube diameter are, the more lately the bending process is developed to steady forming, the more obvious the nonlinear changing trend of springback angle with bending angle is when the bending angle is small, even that the springback angle changes very little with the bending angle. The smaller bending radius and tube diameter are, the larger the springback angle is when the bending angle is small, and the smaller the springback angle is when the bending angle is big. The effect of bending radius is bigger than that of tube diameter.

3) The larger elastic modulus and hardenability value are, the smaller the springback angle is, and the more obscure the nonlinear changing trend of springback angle with bending angle is before steady forming. The larger yield stress and strength factor are, the larger the springback angle is, and the more obvious the nonlinear changing trend of springback angle with bending angle is before steady forming. The significance of effect of these four parameters elastic modulus E, strength factor K, hardenability value n to yield stress σ_s become weaker and weaker.

[1] YANG He, LIN Yan, SUN Zhi-chao. Review of advanced plastic processing technology and tube forming facing 21st century [A]. Symposium of 2nd China Science Association annual Conference [C]. Beijing: Press of Science and Technology, 2000. 745-746. (in Chinese)

[2] YANG H, ZHAN M, LIU Y L. Some advanced plastic processing technologies and their numerical simulation [J]. Journal of Materials Processing Technology, 2004, 151: 63-69.

[3] GU Rui-jie, YANG He, ZHAN Mei. Effect of mandrel on the cross section quality of thin-walled tube NC bending [J]. Trans Nonferrous Met Soc China, 2005, 15(6): 266-271.

[4] GU Rui-jie, YANG He, ZHAN Mei. Effect of friction on the cross section quality of thin-walled tube NC bending [J]. Trans Nonferrous Met Soc China. (accepted)

[5] LI H Z, FAGERSON R, STELSON K A. A Method of adaptive control of rotary-draw thin-walled tube bending with springback compensation [J]. Transactions of NAMRI/SME, 1994, XXII: 25-28.

[6] WANG W C, STELSON K A. Computer aided manufacturing for three-dimensional tube bending with on-line springback compensation [J]. Transactions of North American Manufacturing Institute, 1991. 70-76.

[7] PAN K, STELSON K A. On the plastic deformation of a tube during bending [J]. Journal of Engineering for Industry, Transactions of NAMRI/SME, 1995, 117: 494-500.

[8] LOU Hua-zhou, STELSON K A. Three-dimensional tube geometry control for rotary draw tube bending, part 1: bend angle and overall tube geometry control [J]. Journal of Manufacturing Science And Engineering, 2001, 123: 258-265.

[9] LOU Hua-zhou, STELSON K A. Three-dimensional tube geometry control for rotary draw tube bending, part 2: statistical tube tolerance analysis and adaptive bend correction [J]. Journal of Manufacturing Science and Engineering, 2001, 123: 266-271.

[10] AL-QURESHI H A. Elastic-plastic analysis of tube bending [J]. Journal of Machine Tools & Manufacture, 1999, 39: 87-104.

[11] ZHAN M, YANG H, JIANG Z Q. A study on a 3D FE simulation method of the NC bending process of thin-walled tube [J]. Journal of Materials Processing Technology, 2002, 129: 273-276.

[12] YANG He, LIN Yan. Wrinkling analysis for forming limit of tube bending processes [J]. Journal of Materials Processing Technology, 2004, 152: 363-369.

[13] LI H, YANG H, ZHAN M, GUO L G, GU R J. Wrinkling limit based on fem virtual experiment during nc bending process of thin-walled tube [J]. Materials Science Forum, 2004, 471-472: 498-502.

[14] TRANA K. Finite element simulation of the tube hydroforming process—bending, preforming and hydroforming [J]. Journal of Materials Processing Technology, 2002, 127: 401-408.

[15] YANG J B, JEON B H, OH S I. The tube bending technology of a hydroforming process for an automotive part [J]. Journal of Materials Processing Technology, 2001, 111: 175-181.

[16] OLIVEIRA D A, WORSWICK M J, GRANTAB R, WILLIAMS B W, MAYER R. Effect of forming process variables on the carshworthiness of aluminum alloy tubes [J]. International Journal of Impact Engineering, 2006, 32: 826-846.

(Edited by LI Yan-hong)

Foundation item: Project(50225518) supported by the National Science Foundation of China for Distinguished Young Scholars; Projects(50175092; 59975076) supported by the National Natural Science Foundation of China; Project supported by the Teaching and Research Award Program for Outstanding Young Teachers in Higher Education Institutions of MOE, PRC; Project(04H53057) supported by the Aeronautical Science Foundation of China; Project(Z200518) supported by the Graduate Starting Seed Fund of Northwestern Polytechnical University; Project(20020699002) supported by the Specialized Research Fund for the Doctoral Program of Higher Education

Corresponding author: YANG He; Tel: +86-29-88495632; Fax: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn