DOI： 10.11817/j.issn.1672-7207.2020.06.015
不同湍流边界层中高层建筑模型气动力特性
李石清1, 2,王汉封2,罗元隆3,罗振兵1
（1. 国防科技大学 空天科学学院，湖南 长沙，410073；
2. 中南大学 土木工程学院，湖南 长沙，410075；
3. 淡江大学 工学院，中国 台北，251301）
摘要:在模型高宽比(H/d)为5，基于来流风速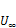
与模型宽度d的雷诺数Red =6.0×104时，通过风洞试验研究2种湍流边界层中正方形截面高层建筑简化模型的气动力特性，并对模型表面脉动风压进行本征正交分解法(POD)分析。研究结果表明：湍流边界层中模型时均阻力系数
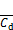的最大值出现在自由端附近，脉动升力系数
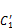的最大值出现在模型中间高度附近。不同湍流边界层中模型侧面中间高度处平均风压系数
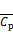与脉动风压系数
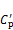的分布差异较大；在湍流度较小的工况C中，脉动升力的周期性较强，两侧风压脉动由反对称状态主导；在湍流度较大的工况A中，模型侧面可能出现间歇性再附，两侧风压脉动转变为对称状态主导，脉动升力减小，且周期性减弱。
关键词:高层建筑；有限长方柱；湍流边界层；气动力特性；本征正交分解法(POD)
中图分类号:TU97 文献标志码:A
文章编号:1672-7207（2020）06-1606-09
Aerodynamic characteristics of square high-rise building models in different turbulent boundary layers
LI Shiqing1, 2, WANG Hanfeng2, LO Yuanlung3, LUO Zhenbing1
(1. College of Aerospace Science and Engineering, National University of Defense Technology,Changsha 410073, China；
2. School of Civil Engineering, Central South University, Changsha 410075, China；
3. College of Engineering, Tamkang University, Taipei 251301, China)
Abstract: The characteristics of aerodynamic forces on a simplified square high-rise building model immersed in two different turbulent boundary layers were experimentally investigated through wind tunnel tests, and the proper orthogonal decomposition(POD) method was adopted to analyze the fluctuation pressure on the model, when the model aspect ratio H/d was 5, and the Reynolds number was 6.0×104 which was based on the oncoming flow velocity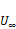 
and the width d. The results show that the maximum 
appears near the free end, while the maximum 
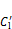appears near the middle-span of the model. The distribution of 
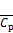and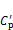 
on the two side faces of the model exerts obvious difference near the middle-span region for the two tested turbulent boundary layers. Particularly, for the one with lower turbulence intensity, the periodicity of lift is relatively stronger, and the pressure on side faces is dominated by anti-symmetrical mode. For the one with higher turbulence intensity, the predominant mode of pressure on side faces becomes symmetrical, resulting in smaller fluctuation lift with weakened periodicity.
Key words: high-rise buildings; finite-length square cylinder; turbulent boundary layer; aerodynamic characteristics; proper orthogonal decomposition(POD)
近年来，由于商业和居住的需要，高层建筑的数量急剧增加。在研究高层建筑风荷载时，可将其视为一端固定于壁面、另一端为自由端的有限长钝体[1-2]，从钝体空气动力学的角度分析其气动力特性。由于受底部边界层和自由端影响，其尾流结构一般由顶部涡(tip vortex)、展向涡(spanwise vortex)和底部涡(base vortex)共3部分构成[3-4]，且有限长钝体尾流结构随高宽比(H/d)变化而显著变化[5-7]。有限长方柱绕流中展向涡会随机出现2种不同状态：一种是大尺度涡团交替脱落的反对称形态，类似卡门涡街；另一种是大尺度涡团对称脱落形态[8-10]。相应地，其气动力也存在2种完全不同的状态[2,10]。现实中的高层建筑处于大气边界层中，研究大气边界层中有限长方柱的气动力特性和不同湍流边界层条件对其气动力的影响规律，对于高层建筑的抗风设计意义重大。徐安等[11]通过风洞试验研究了B和D这2类地貌[12]下联邦航空咨询委员会(CAARC)标模的气动力特性，发现随高度降低而增大的湍流度对CAARC标模顺风向荷载均方根影响不大，而对横风向荷载均方根的影响较大。王汉封等[1]通过风洞试验研究了均匀流和湍流边界层中H/d=5的方柱气动力特性，发现湍流边界层的存在能削弱有限长正方形棱柱脉动风压与气动力的双稳态现象并增大其脉动升力与脉动阻力。以上研究结果表明，湍流边界条件对有限长方形棱柱气动力影响较大，不同的湍流边界条件(例如B和D地貌)下同一模型的气动力规律也不尽相同，有待进一步详细研究并揭示边界层条件对气动力的影响机理。本文通过风洞试验，测量了H/d=5的正方形截面高层建筑简化模型在“建筑物耐风设计规范及解说”[13]规定的A和C这2类地貌下的瞬时风压分布，系统研究不同风场条件下模型气动力的时均特性、瞬态特性并对脉动风压进行本征正交分解(POD)分析，探讨湍流边界层对气动力的影响规律和机理。
1 试验介绍
本试验在中国台湾淡江大学直流开放式风洞中完成。该风洞试验段长15.0 m，宽2.2 m，高2.0 m，风速为1~28 m/s，湍流度小于1%。试验所用简化高层建筑模型为一个正方形截面棱柱，高H=0.5 m，宽d=0.1 m，高宽比H/d=5。模型带来的风洞堵塞度约为1.13%，其影响可忽略不计。模型固定于风洞底面，其中一面正对来流方向。模型与坐标系定义如图1所示。沿模型高度方向布置14层测压点，分别位于量纲一高度z/d为0.2，0.8，1.3，1.8，2.3，2.7，3.0，3.3，3.6，3.9，4.2，4.5，4.7和4.9处，本文中量纲一高度用z*表示，右上角“*”表示该变量为量纲一的量。模型每层共28个测点，每个面各7个，如图1所示。图中A面为迎风面，C面为背风面，B和D面为侧面。各压力测点与扫描阀对应通道连接。本试验使用的是Scanivalve公司RADBASE3200压力信号处理系统和ZOC33压力感应器模组，扫描阀各通道采样频率为200 Hz，采样时间为143 s，各测点采样样本总数为28 600。
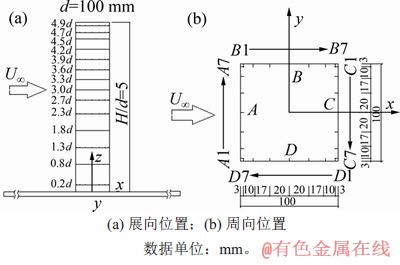
图1 试验模型与坐标系定义示意图
Fig. 1 Experimental setup and definition of coordinates system
利用尖塔与粗糙元[14]，在风洞试验段内模拟2种湍流大气边界层。尖塔与粗糙元摆设如图2所示。边界层内平均风速U、湍流度Iuu与量纲一湍流积分尺度Lu*分布如图3所示，Lu*定义为湍流积分尺度Lu与模型宽度d之比。这2种边界层分别对应规范[13]中的A和C这2类地貌的大气边界层条件，以下简称工况A与工况C。平均风剖面与湍流度分布规律分别为：
图2 尖塔与粗糙元摆设示意图
Fig. 2 Arrangement of spires and roughness elements
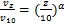(1)
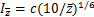(2)
式中：α和c为经验参数；vz为高度为z处的实际风速；v10为10 m高度处的基准风速；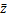
为等效结构高度，其值为0.6h(h为所需要计算湍流度处的高度)，但不可小于
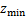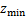(为工况A和C地面粗糙度，分别取18.0 m和4.5 m)。工况A和工况C中，c分别为0.45和0.20，α分别为0.32和0.15。在2类大气边界层条件下，风洞边界层厚度都大于模型高度H，即试验中模型全部处于湍流边界层内，图3中用水平虚线表示模型顶部高度对应曲线。
本文中，以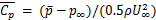
将平均风压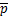
量纲一化为平均风压系数
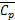，量纲一参考风速选取风洞入口来流风速
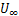，也是湍流边界层的梯度风风速9 m/s，对应雷诺数为Red=6.0×104。其中，
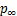为静压，ρ为空气密度，上划线“﹣”表示平均值。需要强调的是，虽然本文所选取雷诺数与实际高层建筑的雷诺数有所差别，但已有研究表明[1]，不同边界条件下方形棱柱气动力均无明显雷诺数效应。
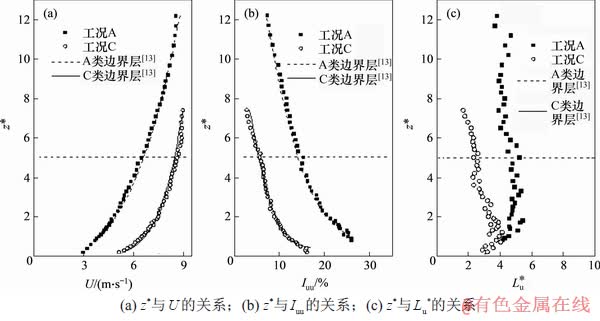
图3 2种试验来流条件
Fig. 3 Two tested oncoming flow conditions
2 POD方法简介
本征正交分解法POD (proper orthogonal decomposition)是分析复杂随机脉动风压场的有效方法。POD采用时间和空间相分离的分析方法，将结构表面的脉动压力场分解为与空间位置无关的时间随机函数主坐标和仅取决于空间位置的多阶本征模态。目前，POD分析方法在风压场的重建和预测等方面已得到广泛运用[15-16]。
本文采用的POD算法是由SIROVICH提出的快照POD(snapshot POD)算法[17]。先将瞬时压力场分解为时均压力场和脉动压力场，即
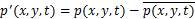(3)
再将脉动量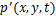
进行如下分解：
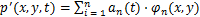(4)
式中：x和y分别为模型表面测点的坐标位置；t为时间；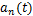
为仅与时间有关的模态系数；
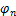(x,y)为仅与空间位置相关的脉动风压POD模态。实际上，求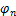(x,y)等价于求解以下最大值问题：
max
(5)
且满足
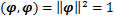(6)
同时，利用原有函数空间快照脉动量的线性组合来表示空间模态，即
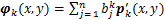(7)
利用变分法，结合式(5)和(7)转化为以下特征值问题：
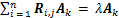(8)
式中：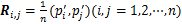
；
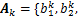
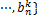(k=1,2,
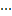,n)；矩阵R为对称阵，且存在对应特征值
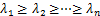。从而可得POD基函数空间：
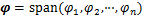(9)
值得注意的是：式(8)中各阶模态特征值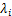
占所有模态特征值之和的比例具有明确的物理意义，它表征对所求系统总能量的贡献能力[18]。该系统总能量可以表示为
，第i阶模态所占总能量贡献率
。
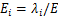3 结果与讨论
3.1 时均结果
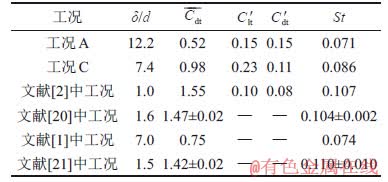
2种工况下模型的全局平均阻力系数
、脉动阻力系数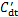
、脉动升力系数
和斯托劳哈数St见表1。其中，
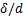表示试验中边界层厚度与模型宽度的比值，当该比值较小时，可近似认为模型处于均匀流条件。由表1可知：当均匀流或边界层较薄时，H/d=5的方柱模型为1.5左右，湍流边界层的存在使得明显减小，且地面粗糙度[12]更大的工况A中减小幅度更大；工况A中模型的和分别为工况C中对应值的53%和65%。值得注意的是，此时工况A中模型的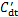反而大于工况C中的对应值，这表明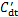和随湍流边界层变化的变化趋势并不一致。结合文献[1]中有限长正方形棱柱模型所处的边界条件，从均匀流到湍流边界层变化时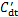和都明显增大这一规律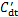，和随湍流边界层的变化规律可能是：地面粗糙度变化带来的边界条件变化会使得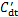先增大后减小，而则一直增大。另外，需要强调的是，本文中以梯度风风速为量纲一参考风速。虽然不同工况中来流风速相同，但模型在不同湍流边界层中当地速度差别很明显，导致力系数有明显差别。采用梯度风风速为参考风速并未消除来流风速的影响，本文的部分讨论是在速度剖面和湍流度的双重影响下进行的。关于参考风速的选择对分析结果造成的影响，仍有待进一步探讨。
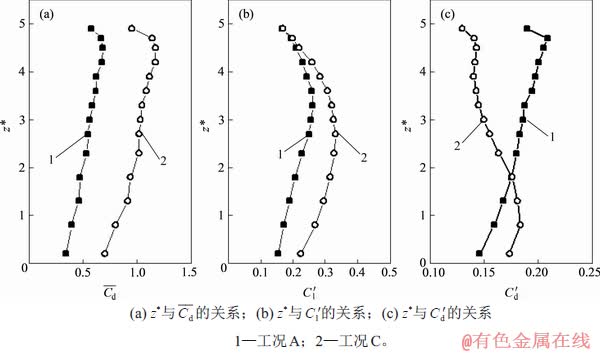
图4 不同高度处局部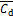
，
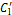和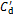
Fig. 4 Local 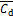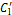，and 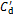at different spanwise positions
表1 方柱模型总体气动力系数(H/d=5)
Table 1 Aerodynamic coefficients of square prism (H/d=5)
为进一步说明湍流大气边界层中方形高层建筑模型的气动力特性，2种工况下模型不同高度处的局部平均阻力系数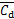
、脉动阻力系数
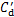与脉动升力系数
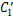见图4。从图4可以看出2种工况下气动力的某些规律是类似的。首先，2种工况下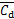的最大值出现在z* =4.5的自由端附近，并随着z*减小而逐渐减小；其次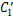，的最大值始终出现在模型中间高度附近，这是因为受边界层与下扫流的共同影响，模型中间高度附近的展向涡脱最强[19]。但工况A中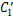仅为工况C对应值的一半左右。值得注意的是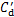，与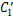在2种工况下随湍流边界层变化的不一致趋势更明显。例如，工况C中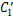沿全部高度都比工况A的大；除模型底部处，工况A中其余高度处局部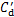都明显大于工况C中对应值，这与表1中工况A与工况C的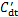变化规律相吻合。
图5所示为三维方柱模型表面的平均风压系数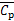
的分布。从图5可见：迎风面上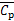随z*的变化发生显著变化，最大风压出现在模型中上部，且在相同梯度风速下，2类工况中迎风面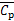存在差异，这是湍流边界层内存在速度剖面造成的；其次，整个背风面上平均风压的分布较均匀，这与均匀流中背风面风压分布也存在不同之处[1]。文献[1]指出，在均匀流工况下，方柱背风面上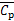的分布沿高度方向上变化明显比湍流边界层工况中的大，这说明湍流边界层起到了使背风面呈均匀分布的作用。此外，在2个侧面上，几乎呈对称分布。需要注意的是，工况A中方柱前沿的绝对值比方柱后沿的大，而工况C中与之相反，即随着湍流度增大，方柱侧面中间高度上的负压极值从后沿向前沿转移。这可能是由于工况A中流动在方柱前沿边角处分离后，随后在侧面出现了间歇性再附[22-23]，而工况C中上述再附现象较弱。图6(a)所示为均匀流和小湍流度的工况C下方柱侧面流动示意图，在此工况下，方柱侧面不出现再附或可能以极低概率出现再附；在工况A下，方柱侧面出现明显的间歇性再附，如图6(b)所示。
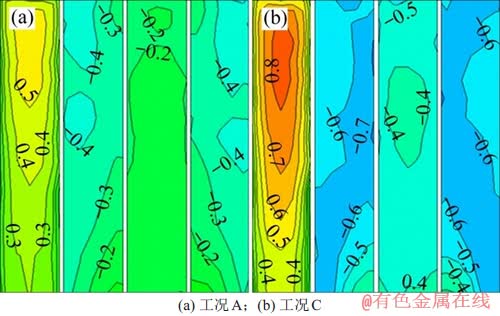
图5 模型表面的
分布
Fig. 5 Distribution of
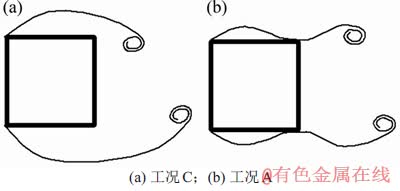
图6 方柱侧面流动情况
Fig. 6 Flow of lateral sides on square prism
图7所示为模型表面脉动风压系数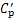
的分布。从图7可以发现：无论是在工况A还是在工况C下，湍流边界层中侧面的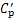都略比迎风面与背风面的大，这与柱体两侧旋涡脱落密切相关[24]；在2种边界条件下，模型中间高度处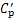都略比模型底部和自由端处的大，这是由于壁面附近的底部涡和自由端后的下扫流干扰了柱体两侧的旋涡脱落[25]。需强调的是，工况C中模型侧面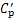的极大值区域出现在后沿；工况A中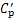极大值区域从后沿向前沿移动。这一现象与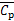的变化趋势相对应，这可能是因为工况A中湍流度增大造成的间歇性再附，改变了两侧面分离泡的位置，造成极大值区域向前沿迁移。结合均匀流中两侧面的风压系数分布[1]可推测，在工况A和C中可能均存在一定程度上的分离剪切流间歇性再附。从均匀流到湍流条件下，来流湍流度增加，使得侧面分离剪切流对方柱侧面回流区自由流体的夹带和干扰增强，间歇性再附发生概率提高[22,26]。
图7 模型表面的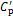
分布
Fig. 7 Distribution of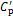
3.2 瞬时结果
图8(a)和(b)所示分别为工况A与工况C下模型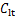
与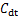
时程及升力的短时傅里叶变换(STFT)结果，并用实线标识了这2种工况下模型的(其中，t为时间，f为频率)。从图8可以看出：工况A中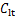脉动幅度明显小于工况C中对应值，而工况A中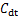脉动幅度则大于工况C中对应值；工况A下模型的围绕较小的进行较大幅度脉动，而工况C中脉动程度较小但时均值较大，这与表1所示规律一致。这进一步表明湍流边界层“粗糙”程度增大会对气动力时均特性与脉动特性带来不同程度的影响，在结构气动设计时应予以重视。由图8和表1可知：模型横风向气动升力的脉动程度较大。横风向气动力决定了其横向振动特性，是结构设计的控制性因素之一。为讨论横风向气动力的频域特性，图8还分别给出了工况A与工况C下模型的总体横向气动升力经短时傅里叶变换所得时频谱图。从图8可以看出：工况C中升力脉动更强，体现在其脉动周期性更强，且在时间上更连续；而工况A中虽然在时间上连续的“亮斑”较少，但升力脉动对应的频域更宽；工况C下的升力脉动比工况A的强。这可能与2个因素有关：首先，工况C中对应的来流风速较高，这使得升力脉动的幅值较大；其次，工况C中升力周期性较强是因为其来流湍流度较小，工况A中升力脉动较弱，与来流湍流度增大时所诱导的间歇性再附密切相关[22]。需要指出的是工况A中升力仍存在一定程度周期性波动，这表明即使工况A中侧面分离剪切流间歇性再附的概率较高，也无法消除旋涡脱落对升力脉动的主导作用，由于旋涡脱落的强控制作用，工况A的升力仍表现出周期性波动。结合图5和图7中侧面风压的变化规律，进一步说明间歇性再附能主导侧面风压变化[22]，但只能从一定程度上影响升力脉动。
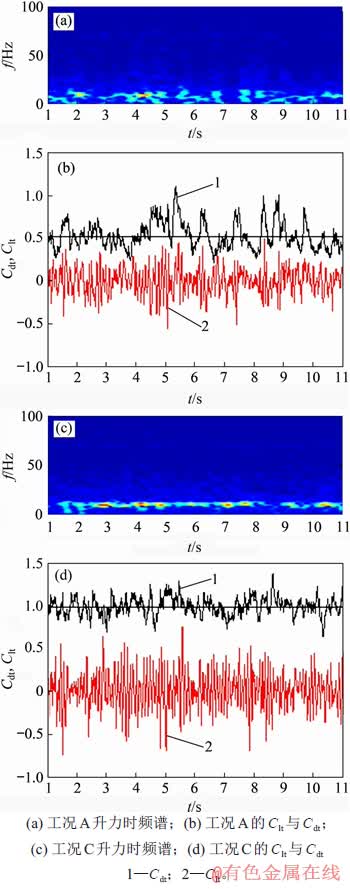
图8 瞬时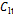
，
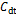与升力短时傅里叶变换结果
Fig. 8 Instantaneous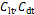 
and time-frequency spectrum of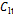
3.3 POD分析结果
模型表面脉动风压的POD分析能够识别不同尺度的压力波动结构，并给出各尺度结构对风压脉动的贡献率。图9所示为各模态对表面风压脉动的贡献率，以比较工况A与工况C的气动力特性。从图9可见：随模态数增加，其对风压脉动的贡献逐渐减小。5阶及以上模态对风压脉动的贡献率都小于5%，因此，本文仅关注起主导作用的前4阶模态。
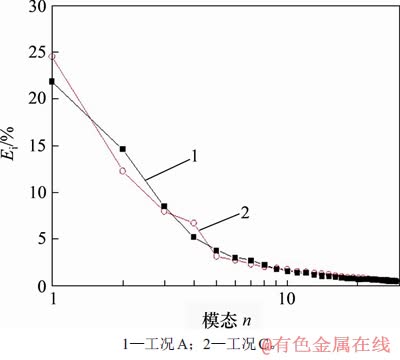
图9 主要POD模态能量贡献率Ei
Fig. 9 Contributions to pressure fluctuation from main POD modes
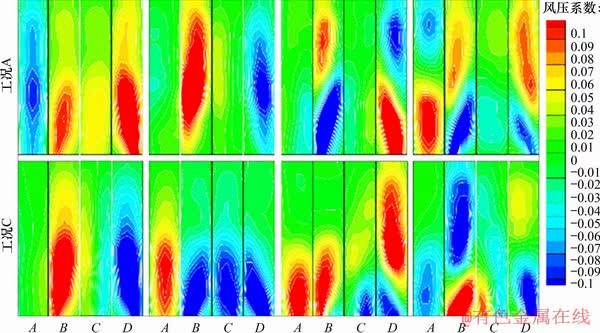
图10 脉动风压的前4阶POD模态
Fig. 10 The first four POD modes of fluctuation pressure
图10所示为经POD分析获得的前4阶(从左至右分别为1~4阶)模态。从图10可见：工况A和C这2种工况的POD模态存在定性区别；工况A中mode 1和mode 4对应的风压呈对称分布，即柱体侧面B和D面上的风压具有相同符号，而迎风面A与背风面C风压符号相反，由此可知工况A的mode 1和mode 4仅对脉动阻力有贡献，而其对脉动升力的贡献基本为零。而工况A的mode 2中，B和D面上风压呈反对称分布，即侧面B和D的风压符号相反，仅对脉动升力有较大贡献。对于工况A的mode 3，尽管其B和D面风压分别呈反对称与对称分布，但B和D侧面上的脉动风压在柱体上、下部分的符号相反，其对模型总体脉动升力的贡献非常有限，仅对侧向倾覆力矩有贡献，因此，对于工况A，仅mode 2对其脉动升力起主导作用。类似地，工况C中仅有mode 1对模型脉动升力起决定作用，而mode 2，mode 3和mode 4的贡献非常有限，这与均匀流中和较小湍流度时的结果非常类似[25,27]。由图9可知，工况A中对脉动升力起主要作用的mode 2其贡献率仅占总风压脉动的15%左右，而工况C中对脉动升力起主要作用的mode 1对风压脉动贡献率达25%左右。这2种工况前4阶模态的风压脉动总量中，工况C中反对称模态对风压脉动的贡献率明显大于工况A对应值。因此，工况C中模型的脉动升力应显著大于工况A中对应值，这与图8所示结果是一致的。
对比二维方柱风压POD分析结果[25]可以发现：对升力脉动起主要作用的mode 1形态为反对称形态，且其贡献率占风压脉动的83%左右，远远高于本试验中三维方柱反对称模态的贡献率(15%和25%)，由此可知三维方柱尾流中的展向涡脱强度远比二维方柱的弱，其脉动升力也远小于二维方柱对应值。此外，随着来流湍流度增大，伴随着可能出现的间歇性再附，三维方柱表面风压脉动由反对称状态主导转变为对称状态主导，其脉动升力将进一步减小。
4 结论
1) 大气边界层中高层建筑方柱模型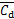的最大值出现在自由端附近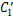，的最大值出现在模型中间高度附近；由于大气边界层的影响，工况A中模型的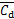和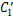明显小于工况C中对应值，而
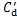则大于的工况C中对应值。
2) 工况A中模型侧面前沿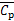的绝对值比后沿的大，而工况C中与之相反。工况C中模型侧面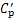的极大值区域出现在侧面后沿，覆盖了中下部到中上部区域，工况A中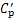极大值区域从后沿向前沿移动，出现在侧面中段和中后沿。
3) 在湍流度较小的工况C中，脉动升力的周期性较强。随着来流湍流度增大，伴随着可能出现的间歇性再附，模型表面风压脉动由反对称状态主导转变为对称状态主导，脉动升力的周期性减弱，其脉动升力减小。
参考文献：
[1] 王汉封, 杨帆, 邹超. 边界条件对有限长正方形棱柱气动力的影响 [J]. 振动与冲击, 2016, 35(5): 39-46.
WANG Hanfeng, YANG Fan, ZOU Chao. Effects of boundary layer conditions on aerodynamic forces of a finite-length square prism [J]. Journal of Vibration and Shock, 2016, 35(5): 39-46.
[2] 王汉封, 赵东伟, 邹超, 等. 高宽比为5的悬臂正方形棱柱气动力特性[J]. 实验流体力学, 2015, 29(6): 8-15.
WANG Hanfeng, ZHAO Dongwei, ZOU Chao, et al. Aerodynamic forces of a cantilevered square prism with aspect ratio of 5[J]. Journal of Experiments in Fluid Mechanics, 2015, 29(6): 8-15.
[3] WANG Hanfeng, ZHOU Yu. The finite-length square cylinder near wake[J]. Journal of Fluid Mechanics, 2009, 638: 453-490.
[4] SUMNER D. Flow above the free end of a surface-mounted finite-height circular cylinder: a review[J]. Journal of Fluids and Structures, 2013, 43: 41-63.
[5] ROSTAMY N, SUMNER D, BERGSTROM D J, et al. Local flow field of a surface-mounted finite circular cylinder[J]. Journal of Fluids and Structures, 2012, 34: 105-122.
[6] SUMNER D, ROSTAMY N, BERGSTROM D J, et al.Influence of aspect ratio on the flow above the free end of a surface-mounted finite cylinder[J]. International Journal of Heat and Fluid Flow, 2015, 56: 290-304.
[7] SUMNER D, HESELTINE J L. Tip vortex structure for a circular cylinder with a free end [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(6/7): 1185-1196.
[8] WANG Hanfeng, CAO Huilan, ZHOU Yu. POD analysis of a finite-length cylinder near wake[J]. Experiments in Fluids, 2014, 55(8): 1790-1805.
[9] 王汉封, 徐萌霞. 有限长正方形棱柱绕流的双稳态现象[J]. 力学与实践, 2013, 35(3): 46-50.
WANG Hanfeng, XU Mengxia. Bistable phenomenon of the flow around a finite-length square prism[J]. Mechanics in Engineering, 2013, 35(3): 46-50.
[10] SATTARI P, BOURGEOIS J A, MARTINUZZI R J. On the vortex dynamics in the wake of a finite surface-mounted square cylinder[J]. Experiments in Fluids, 2012, 52(5): 1149-1167.
[11] 徐安, 谢壮宁, 葛建斌, 等. CAARC高层建筑标准模型层风荷载谱数学模型研究[J]. 建筑结构学报, 2004, 25(4): 118-123.
XU An, XIE Zhuangning, GE Jianbin, et al Mathematical model research of power spectrum of wind loads on CAARC standard tall building model[J]. Journal of Building Structures, 2004, 25(4): 118-123.
[12] GB 50009—2012. 建筑结构荷载规范[S].
GB 50009—2012. Load code for the design of building structures[S].
[13] 1030805400. 建筑物耐风设计规范及解说[S].
1030805400.Load code and details for the wind resistance design of building structures[S].
[14] 石碧青, 洪海波, 谢壮宁, 等. 大气边界层风洞流场特性的模拟[J]. 空气动力学学报, 2007, 25(3): 376-380, 395.
SHI Biqing, HONG Haibo, XIE Zhuangning, et al. Wind tunnel simulation of atmospheric boundary layer[J]. Acta Aerodynamica Sinica, 2007, 25(3): 376-380, 395.
[15] 李方慧, 倪振华, 沈世钊, 等. POD原理解析及在结构风工程中的几点应用[J]. 振动与冲击, 2009, 28(4): 29-32, 201.
LI Fanghui, NI Zhenhua, SHEN Shizhao, et al. Theory of POD and its application in wind engineering of structures[J].Journal of Vibration and Shock, 2009, 28(4): 29-32, 201.
[16] 邹垚, 梁枢果, 邹良浩. 基于本征模态修正的POD法在风场重建中的应用[J]. 土木工程学报, 2010, 43(S1): 305-309.
ZOU Yao, LIANG Shuguo, ZOU Lianghao. Reconstruction of fluctuating wind pressure field by applying POD of eigenvector correction[J]. China Civil Engineering Journal, 2010, 43(S1): 305-309.
[17] SIROVICH L. Turbulence and the dynamics of coherent structures. II. Symmetries and transformations[J]. Quarterly of Applied Mathematics, 1987, 45(3): 573-582.
[18] CHIEKH M B, MICHARD M, GUELLOUZ M S, et al. POD analysis of momentumless trailing edge wake using synthetic jet actuation[J]. Experimental Thermal & Fluid Science, 2013, 46: 89-102.
[19] KAWAI H, OKUDA Y, OHASHI M.Near wake structure behind a 3D square prism with the aspect ratio of 2.7 in a shallow boundary layer flow[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2012, 104/105/106: 196-202.
[20] OGUNREMI A R, SUMNER D. The effect of a splitter plate on the flow around a finite prism[J]. Journal of Fluids and Structures, 2015, 59: 1-21.
[21] SUMNER D, ROSTAMY N, BERGSTROM D J, et al.Influence of aspect ratio on the mean flow field of a surface-mounted finite-height square prism[J]. International Journal of Heat and Fluid Flow, 2017, 65: 1-20.
[22] KAREEM A, CERMAK J E.Pressure fluctuations on a square building model in boundary-layer flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1984, 16(1): 17-41.
[23] 孙虎跃, 叶继红. 基于PIV技术的平屋盖表面分离泡流动结构研究[J]. 工程力学, 2016, 33(11): 121-131.
SUN Huyue, YE Jihong. 3D characteristics of separation bubbles around flat roofs by piv technique[J]. Engineering Mechanics, 2016, 33(11): 121-131.
[24] 邹超. 典型高层建筑风荷载及其影响因素的实验研究[D]. 长沙: 中南大学土木工程学院, 2014: 38-39.
ZOU Chao. Experimental investigation on the wind load of typical high-rise building and its influence factors[D]. Changsha: Central South University. School of Civil Engineering, 2014: 38-39.
[25] WANG Hanfeng, ZHAO Xiaoyan, HE Xuhui, et al. Effects of oncoming flow conditions on the aerodynamic forces on a cantilevered square cylinder[J]. Journal of Fluids and Structures, 2017, 75: 140-157.
[26] LEE B E. The effect of turbulence on the surface pressure field of a square prism[J]. Journal of Fluid Mechanics, 1975, 69(2): 263-282.
[27] KIKUCHI H, TAMURA Y, UEDA H, et al.Dynamic wind pressures acting on a tall building model: proper orthogonal decomposition [J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71: 631-646.
（编辑 陈灿华）
收稿日期： 2019 -06 -22; 修回日期： 2019 -09 -23
基金项目(Foundation item)：国家自然科学基金资助项目(11472312) (Project(11472312) supported by the National Natural Science Foundation of China)
通信作者：王汉封，博士，教授，从事实验流体力学与流动控制研究；E-mail：wanghf@csu.edu.cn
