Crack propagation of Mg-Li alloys by impact load
QU Zhi-ming(曲志明)1, LIANG Xiao-ying(梁晓颖)1, ZHOU Xin-quan(周心权)2, SHI San-yuan(史三元)1
1. School of Civil Engineering, Hebei Engineering University, Handan 056038, China;
2. State Key Laboratory of Coal Resource and Safe Mining, China University of Mining and Technology, Beijing 100083, China
Received 15 July 2007; accepted 10 September 2007
Abstract: Under impact load, using energy estimation and updated finite element method, the crack propagation of Mg-Li alloys was studied, and the relations between high speed impact, time interval and crack propagation velocity were deduced. The effects of impact pattern characteristic parameters such as impact range and time interval on impact fatigue crack growth and propagation rates were discussed. The results show that with the development of crack length, the crack propagation rate along the central sample alloy swiftly increases to the maximum. Then, the crack of other parts has different rate variations. The calculation and simulation results fit well with the experimental ones, which verifies the validity of energy estimation and updated finite element analysis. Impact loading usually induces materials and accelerates the fatigue crack growth.
Key words: crack propagation; Mg-Li alloys; impact load; finite element
1 Introduction
The fracture of Mg-Li alloy materials under impact load is divided into two aspects, the crack initiation behavior and the crack propagation. Fatigue crack propagation under repeated impact load is an important aspect of metal fatigue under acceleration of crack growth rates. Considerable attention has been paid to impact fatigue crack propagation behavior because the Mg-Li alloy plays more and more important role in material application and aviation industry.
1.1 Crack by impact load
The finite element method is widely used in studying crack propagation. The crack body is dispersed into a few units. Based on variation principle, the motion equations about the dispersed time, t, can be deduced into two-order ordinary differential equations. At any time, the displacement, u(t), should satisfy the motion equations at t, t+Δt, t+2Δt, ???, and the displacement, velocity and acceleration are as the hypotheses with the time interval. Thus, the initial acceleration 
is solved while the initial displacement and the velocity 
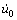are settled. Meanwhile, the stress, strain and factors of stress intensity can be acquired[1-2].
1.2 Central crack in alloy sample
The rectangular Mg-Li alloy is used to study the crack propagation in the central rectangular sample. The normal and shear impact loads are utilized to express the crack propagation[3]. Fig.1 shows the central crack under the impact load[1, 4-5]. In the function K1(t)=K*F{(c1t)/(2a), a/l, b/l}, where K* means the statics factor of stress intensity. F{(c1t)/(2a), a/l, b/l}, the function of crack and structure size, is the dimensionless factor, in which t is changeable. In Fig.2, F{(c1t)/(2a), a/l, b/l} satisfies the condition of l?b?a=10?6?1[1].
Fig.3 shows the central crack of the rectangular alloy sample under the shear impact load[1-6]. 
{t, W/a, H/a} is the structural size and the dimensionless function of time, t. Furthermore, it is the function of such load types as jump load, impulse load and zero-linear ascending to a certain impact load[2, 7], which is shown in Fig.4.
The research work of Mg-Li alloy mentioned above has made significant progress, especially in crack form and development mechanism. Due to broad application prospects of Mg-Li alloy, the effect of crack propagation by impact load was mainly studied in the following sections. Moreover, the time interval influencing crack propagation and algorithm about finite element were deduced and described. The quantitative analysis was done based on the improved finite element methods and, the results were analyzed in detail.
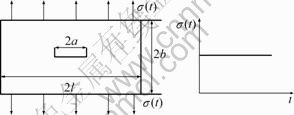
Fig.1 Central crack propagation by impact load
Fig.2 Function F changing with time
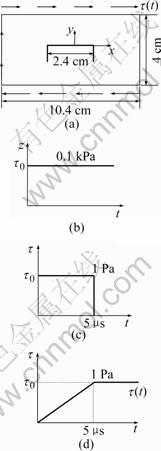
Fig.3 Central crack propagation by shear impact
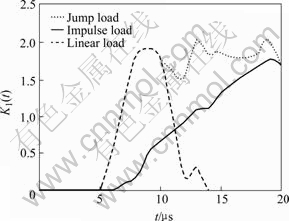
Fig.4 F—t curves at three different loads
2 Energy estimation of crack propagation
Crack propagation is obviously different from static crack, which must consider the inertial effect[2]. Actually, the kinetic energy cannot be ignored. MOTT, the first man who considered this problem in 1948, used the dimension analysis to study the crack propagation. Due to the solution of fractural statics, the displacement field has the formation near the top of crack as follows:
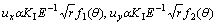(1)
where r and θ are the polar coordinates, f1(θ) and f2(θ) are the distribution functions of angle, respectively. Due to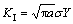 
, Eqn.(1) can be written as follows:
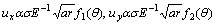(2)
where Y is the geometric factor.
From dimension analysis, r∝a, thus, Eqn.(2) can be expressed as
ux=c1σaE-1, uy=c2σaE-1 (3)
where c1 and c2 are dimensionless parameters. In Eqn.(3), E is a constant that is not related to c1, c2 and σ. The crack length, a, is the function of t while the crack propagates. Through derivation by t, Eqn.(3) is changed into the following form:
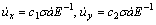(4)
where the sign “·” is the partial derivative to time, t. The kinetic energy of the rectangular alloy sample with crack is
(5)
where ρ is the density of alloy sample, Ω the integral domain. Substituting Eqn.(4) into (5), the following formula is deduced.
(6)
Only the parameter a is related to the crack length. Thus, the domain area of Ω has the same dimension with a2. The dimension of a2 is the same with that of the right derivation in Eqn.(6). Let κ be the proportional coefficient, then
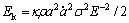(7)
FANG[1-2] has discussed the kinetic energy of crack propagation. If the releasing rate of strain energy G is always higher than the crack propagation resistance, the instable crack propagation R is created. The residual G-R can be changed into kinetic energy. Because G and R are the energies of crack propagation per unit, the energies are GΔa and RΔa respectively while the crack propagates at Δa. Thus
ΔEk=GΔa-Rδa (8)
By integrating Eqn.(8), we can get
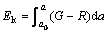(9)
where a0 is the critical dimension when the instable crack propagates.
Let R and σ be the constants, then G is solved by statics as G=πσa2/E. Eqn.(9) can be expressed as
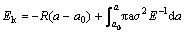(10)
when the instability is started, R=G0=πa0σ2E-1, substituting it into Eqn.(10) yields
Ek=πσ2E-1(a-a0)2 (11)
Comparing Eqn.(7) with (11), then
(12)
where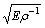 
is the acoustic velocity in Mg-Li alloy sample, which is measured by experiment. When a0a-1→0, 
, thus k=43.49.
From Eqn.(7), a simple formula of kinetic energy calculation is given. From the formula, the effect of kinetic energy cannot be ignored when the crack velocity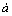 
is not very small.
3 Updated finite element analysis
Due to dynamic impact load, the crack will propagate swiftly. Part of the boundary also moves, which belongs to the problem of motion boundary. Even if the governing equation is linear, the boundary problem is still non-linear. In order to solve the problem of non-linear effect, an algorithm, on the basis of the finite element method, is put forward by KEEGSTRA[1-2] and deduced again.
3.1 Algorithm principle
Let the acceleration at t=t0, t=t0+Δt and t=t0-Δt be 
and 
, respectively, where 
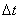is the time interval. A second order Largrange polynomial is adopted[1-2, 8].
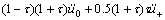(13)
where τ=(t-t0)/Δt. After twice derivative at t=t0(τ=0), Eqn.(13) is changed into 
and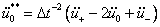 
. Substituting 
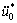and 
at t=t0 into Taylor expansion, the displacement and velocity at t=t0+Δt are expressed as
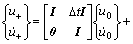
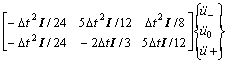(14)
where I is the unit matrix, 0 the zero matrix.
At the right hand of Eqn.(14), 
is unknown. At the beginning of calculation, let be . Using Eqn.(14), u+ and 
can be calculated. More accurate calculation of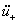 
can be solved by the rearrangement of motion equation. The calculation process is not interrupted until is convergent. The method is just the direct integration scheme whose advantage is that the non-linearity caused by crack propagation can be easily adjusted in the program through changing K, C and M.
3.2 Time interval
The stability of algorithm is governed by the time interval. The program modification aims at lessening the time of each time interval and the frequency of time interval. Thus, the upper limit value plays a very important role in program embodied into the finite element method. TANG[2] has pointed out that the time interval should be less than the responding period of the highest natural frequency in the impact system. The period can be decided by the minimal eigenvalue of the system. DET|K-1M-ω-2|=0, where ω is the frequency. The eigenvalue is real and positive because matrice k and m are symmetry positive definite.
In fact, Δt≤1/(4ωmax) is well-guessed, where ωmax is the most natural frequency of the smallest finite unit in the system structure. And another estimation, L/10c1≤Δt≤L/2c1, is given by HARTZMAN and HUTCHINSON, where c1 is the longitudinal wave velocity, L a characteristic length of the minimal finite unit in the system structure. In order to keep stable the calculation, FANG[1-2], practically, gave the expression of ΔT=l/(8c1).
4 Results analysis and comparison
Using sections 2, 3 and the method provided by Refs.[9-12], the crack propagation is simulated by combining with these methods. The meshes division is shown in the 3rd one in Fig.5. And other conditions in detail are illustrated in Refs.[12-18]. The alloy sample is composed of magnesium and lithium. So far, the Mg-Li alloy is the lightest metal material. Its density is from 1 350 to 1 650 kg?m-3, which is only 3/5 to 3/4 of the magnesium alloy. The density of Mg36Li5Zn and Mg36LiAl with high content of lithium is less than 1 000 kg?m-3, which can float on the water. Due to low density, the Mg-Li alloy can keep a certain intensity, which has highly specific strength and modulus. Additionally, it is advantageous at processing property, shock absorption and electromagnetic screening effect. All the features have received enough attention by astronavigation field and ordnance industry. Based on the study, the Mg-Li alloy sample with dimensions of 400 mm×400 mm×10 mm, are used(shown in Fig.5). The velocity of bullet is 10 m/s-1.
4.1 Crack propagation simulation
In Fig.6, the signs A to M represent the node numbers selected in alloy sample during simulation. It can be seen that, under the impact load with bullet average speed of 10 m/s, the crack propagation speed can reach the maximum at the beginning of initial crack. After that, the crack propagation velocity is decreased and then increased swiftly. The propagation process is not finished until the alloy sample is passed through by the bullet completely. In this process, the crack is obviously observed and propagates with the stress action. Actually, different contents of lithium will induce different propagation velocities or rates. The crack propagation rate of Mg-3.3Li alloy sample is of very high speed that will reach 1 160.65 m/s. But the alloy of Mg-14Li is with low speed that is about 899.36 m/s. However, the initial crack time or the time interval is similar basically. Thus, to the single-phase Mg-Li alloy and with the content of lithium increasing, the structure of the alloy sample will be changed greatly under the impact load. From the viewpoint of metallic phase diagram, the dynamic crack propagation rate is obviously decreased because the crystal structure has been transformed into the whole cube structure. The alloy fracture is lowered and the ductile crack propagation will play an important role and increase the alloy toughness.
4.2 Results and comparison
The calculation and experiment results are shown in Figs.7 and 8. Combining macro-mechanism behavior with micro fracture mechanisms, it is indicated that impact fatigue crack growth rates are strongly associated with the micro fracture mechanisms under both loading conditions. The crack growth rate depends on the impact accumulation at the crack tip. The larger the plastic deformation zone, the more serious the plastic deformation degree in impact crack in impact load time interval. The experimental results indicate that the impact fatigue crack growth rate decreases owing to the decrease of plastic deformation. Through comparison with simulation in Fig.6, the calculation and experiment results agree with the simulation.
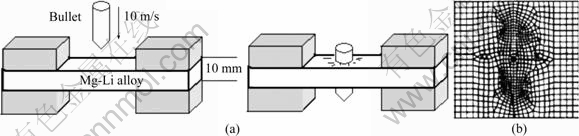
Fig.5 Interaction between bullet and Mg-Li alloy (a) and meshes division (b)
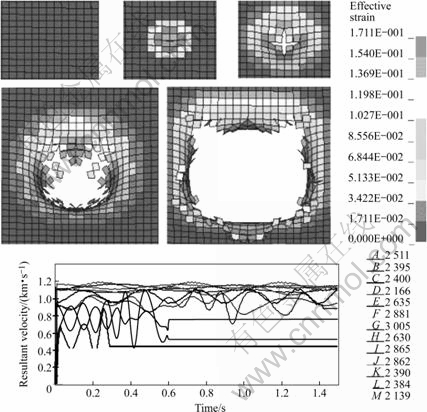
Fig.6 Crack propagation and its velocity changing with time
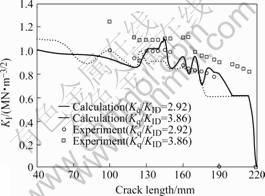
Fig.7 Relation between KI and crack length
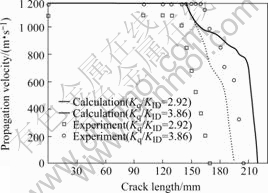
Fig.8 Relations between crack propagation velocity and crack length
5 Conclusions
The impact fatigue crack propagation behavior was investigated. However, an in-depth understanding of impact load crack is not available. This is due to the complexity of impact stress waves propagation and the response of materials to impact stresses. The phenomena such as crack propagation and sample damage are wholly dominated by the plastic deformation and fracture behavior under different loading conditions. In order to obtain a clear understanding of the crack growth behavior and the mechanism of impact crack propagation, investigation on the quantitative relation between impact stress pattern characteristic parameters, the deformation and fracture mechanism for different materials is concentrated. It can be concluded that the effects of impact pattern characteristics on crack propagation are significant and complicated. However, the calculation and experiment and simulation agree with each other while using the energy estimation of crack propagation and the updated finite element analysis.
References
[1] FANG Tian-you. Introduction to fracture dynamics[M]. Beijing: Beijing Institute of Technology Press, 1990. (in Chinese)
[2] FANG Tian-you. Foundation of applied fracture dynamics[M]. Beijing: Beijing Institute of Technology Press, 1992. (in Chinese)
[3] YU Jie, PETER K L, CAI C A, YE Ming-liang. Impact fatigue crack propagation[J]. Guizhou Science, 2000, 18(1/2): 1-10.
[4] WANG Xiao-xia, L? Nian-chun. Dislocation distribution function of model crack under reaction of superimpose and impact loads[J]. Journal of Heilongjiang Institute of Science and Technology, 2007, 17(1): 11-15. (in Chinese)
[5] LIU Xi-guo, ZHAO Hong-ping, WU Yong-1i, ZHANG Shuang-yin. The critical loading surface of a crack under impact[J]. Explosion and Shock Waves, 2001, 21(3): 198-204. (in Chinese)
[6] SHA Gui-ying, XU Yong-bo, HAN En-hou, YU Tao, LIU Lu, GAO Guo-zhong. Dynamic crack propagation behavior of the Mg-Li alloys under high loading rate[J]. Journal of Aeronautical Materials, 2005, 25(5): 50-53. (in Chinese)
[7] LIU Xi-guo, JIANG Yuan-xing, ZHAO Hong-ping. Experimental studies on the initiation of crack in fiber-reinforced composites under impact loading[J]. Explosion and Shock Waves, 2002, 22(2): 111-118.
[8] GUO Yi-zhi, JIN Xian-long, DING Jun-hong, CAO Wen-hong, CHEN Hong. Three-dimensional contact model and algorithm for earthquake response of immersed tunnel[J]. Chinese Journal of Applied Mechanics, 2006, 23(1): 53-57. (in Chinese)
[9] QIN Si-ji, LI Hong-bo, PENG Jia-geng, LI Shuo-ben. Numerical simulation and optimization of clearance in sheet shearing process[J]. Trans Nonferrous Met Soc China, 2003, 13(2): 407-411.
[10] HUANG Ning-kang, YANG Bin, WANG De-zhi. Impact toughness of tungsten films deposited on martensite stainless steel[J]. Trans Nonferrous Met Soc China, 2005, 15(5): 1077-1080.
[11] LIU Yuan, YU Jin-jiang, XU Yan, SUN Xiao-feng, GUAN Heng-rong, HU Zhuang-qi. High-cycle fatigue behavior of nickel-base single crystal superalloy[J]. Trans Nonferrous Met Soc China, 2005, 15(3): 57-60.
[12] BAI Jin-zhe. Theory and example analysis of LS-DYNA3D[M]. Beijing: Science Press, 2005. (in Chinese)
[13] ZHANG Zhi-an, CHEN He-juan. Research on numerical simulation of impact velocity and impact angle to hard target penetration acceleration influence[J]. Journal of System Simulation, 2007, 19(11): 2607-2609. (in Chinese)
[14] ZHANG De-zhi, ZHANG Xiang-rong, LIN Jun-de, TANG Run-di. Numerical simulation of rigid projectile’s normally penetrating into granite targets[J]. Journal of Beijing Institute of Technology, 2004, 13(3): 308-312.
[15] WANG Yong-gang, WANG Li-li. Stress wave dispersion in large-diameter SHPB and its manifold manifestations[J]. Journal of Beijing Institute of Technology, 2004, 13(3): 247-253.
[16] GAO Wen-xue, LIU Yun-tong, YANG Jun, HUANG Feng-lei. Dynamic damage model of brittle rock and its application[J]. Journal of Beijing Institute of Technology, 2003, 12(3): 332-336.
[17] NIELSEN K B, JENSEN M R, DANCKERT J. Optimization of sheet metal forming processes using finite element simulations[J]. Acta Metallurgica Sinica, 2000, 13(2): 531-539.
[18] BAO X G, HE D N, LU D, LI C X, CHENG J L, JIANG J Y. Optimization of autobody panel stamping process based on dynamic explicit finite element method[J]. Acta Metallurgica Sinica, 2000, 13(1): 387-393.
Foundation item: Project(2005CB221506) supported by the National Basic Research Program of China
Corresponding author: QU Zhi-ming; Tel: +86-310-8576536; E-mail: chinaqzm@163.com
(Edited by CHEN Wei-ping)
