Effects of thickness and elastic modulus on stress condition offatigue-resistant coating under rolling contact
来源期刊:中南大学学报(英文版)2010年第5期
论文作者:朴钟宇 徐滨士 王海斗 濮春欢
文章页码:899 - 905
Key words:sprayed-coating; thickness; elastic modulus; maximum stress; von Mises stress; finite element method
Abstract: The distribution and magnitude of surface and subsurface stresses of the single-layer sprayed-coatings on monolithic substrates were investigated by finite element method (FEM). The models of coating configurations with different thicknesses and elastic modulus ratios of coating to substrate were introduced, and the effects of thickness and elastic modulus ratio on the stresses were addressed. The calculation results show that the coating/substrate interface shear stress obviously decreases with increasing coating thickness, due to the location of the maximum shear stress moving away from the coating/substrate interface. At the same time, the magnitude of von Mises stress also declines in the case of thicker coatings. However, the high elastic modulus ratio results in extremely high maximum shear stress and the severe discontinuity of the von Mises stress curves, which leads to the intensive stress concentration on the coating/substrate interface. So the coating configurations with the larger coating thickness and lower difference of elastic modulus between coating and substrate exhibit excellent resistant performance of rolling contact fatigue (RCF).
基金信息:the National Natural Science Foundation of China
J. Cent. South Univ. Technol. (2010) 17: 899-905
DOI: 10.1007/s11771-010-0574-5
![]()
PIAO Zhong-yu(朴钟宇)1, 2, XU Bin-shi(徐滨士)2, WANG Hai-dou(王海斗)2, PU Chun-huan(濮春欢)2
1. School of Mechanical Engineering, Yanshan University, Qinhuangdao 066004, China;
2. National Key Laboratory for Remanufacturing, Academy of Armored Forces Engineering, Beijing 100072, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2010
Abstract: The distribution and magnitude of surface and subsurface stresses of the single-layer sprayed-coatings on monolithic substrates were investigated by finite element method (FEM). The models of coating configurations with different thicknesses and elastic modulus ratios of coating to substrate were introduced, and the effects of thickness and elastic modulus ratio on the stresses were addressed. The calculation results show that the coating/substrate interface shear stress obviously decreases with increasing coating thickness, due to the location of the maximum shear stress moving away from the coating/substrate interface. At the same time, the magnitude of von Mises stress also declines in the case of thicker coatings. However, the high elastic modulus ratio results in extremely high maximum shear stress and the severe discontinuity of the von Mises stress curves, which leads to the intensive stress concentration on the coating/substrate interface. So the coating configurations with the larger coating thickness and lower difference of elastic modulus between coating and substrate exhibit excellent resistant performance of rolling contact fatigue (RCF).
Key words: sprayed-coating; thickness; elastic modulus; maximum stress; von Mises stress; finite element method
1 Introduction
In many types of industrial applications, such as gears, camshafts and rolling bearings, surface damage generates owing to the rolling contact. Rolling contact fatigue (RCF) that is responsible for the failure of aforementioned components, may be defined as cracking or pitting/delamination limited to the near-surface layer of substrates under rolling/sliding contact [1]. Therefore, in many situations of industrial manufacture, one of the key issues is to achieve optimal surface properties of mechanical components. These problems are often solved by surface engineering techniques, e.g., thermal spraying.
The coatings deposited by thermal spray techniques such as plasma spraying, high velocity oxy-fuel, and arc wire, can provide an excellent cost-effective solution for tribological applications in pure rolling or rolling/sliding contact [2-7]. In the case of RCF application of thermal spray coatings, the coating failures can be classified into three categories, i.e., surface abrasion, spalling, and delamination [8]. Stresses (shear stress and von Mises stress) in the coating driven by contact stress are the important factors for RCF failure [9-11]. Therefore, the investigations of the effect of coating parameters (such as geometry and mechanical properties) on these stresses are important for the coating reliability design. Accordingly, a qualitative analysis of distribution and magnitude of these stresses is necessary.
Although previous studies showed that there were some relations between multi-layer and stress distribution in coating configurations, DIAO et al [12- 13] investigated the effect of inter-layer on the stress, ZHANG et al [14] researched the stress distribution in the sandwich coatings, and SAIZONOU et al [15] addressed the stress condition in the functionally graded coatings. In the case of single-layer medium that is widely applied, a few systemic researches on contact problem have been conducted. Therefore, in this work the Hertzian contact response of fatigue-resistant coatings was investigated under pure rolling contact. The effects of different thicknesses and elastic modulus ratios on the distribution of the stress in the sprayed-coatings were addressed. For the theoretical and experimental approaches both fail to successfully predict contact stress and fatigue behavior in the layered media [16-17], the finite element method (FEM) was employed and single-layer models with different thicknesses and elastic modulus ratios were established to analyze the effects on the stresses. Only the elastic deformation of the coating under the frictionless contact was taken into account. The optimal coating thickness and elastic modulus ratio were selected to guide the engineering application.
2 Finite element (FE) calculation
Fig.1 shows the rolling contact FE model between a rigid sphere and the sprayed-coating under a normal load and frictionless condition. The model used to calculate the stress inside the coating driven by elastic contact, was created using the commercial FE analysis code ANSYS. An axial symmetric problem was chosen in order to reduce the data processing time. A Cartesian coordinate system Oxy was introduced. More refined meshes near the contact regions were employed to improve the accuracy of the calculation. The boundary conductions were established, where the displacement of each nodal point on lines AB and CD was constrained in x-direction and that on line BC was constrained in y-direction. The spherical Hertzian elastic contact condition [18] was employed, and the normal contact traction p(x) was investigated by JOHNSON [19] from a half plane solution and given by the following expression:
![]() (1)
(1)
where p0 is the maximum contact stress; a is the contact radius; and x is the distance from the contact center.

Fig.1 FE model of coating configuration
Four kinds of thickness ratios of the coating thickness to the contact radius, i.e., tc/a=0.5, 1.0, 2.0, 4.0 were introduced in the present FE model, where tc is the thickness of the coating. Four kinds of elastic modulus ratios of coating to substrate, i.e., Ec/Es=0.5, 2.0, 4.0, 8.0 were also introduced in FE model, where Ec and Es are the elastic moduli of the coating and the substrate, respectively. For all coating configurations, some conditions were constant, i.e., the maximum contact stress (p0) was 5 GPa, the contact radius (a) was 400 μm, the elastic modulus of substrate (Es) was 200 GPa, Poisson ratios of coating and substrate were both kept at 0.3. When different thicknesses were taken into account, the elastic modulus ratio of coating to substrate was constant, i.e., Ec/Es=2. In the same way, for different elastic moduli, the thickness ratio was constant, i.e., tc/a=2. Moreover, the residuals stresses within the coatings were ignored in all FE models.
3 Results3.1 Stress distribution of coatings with different thicknesses
Hertzian contact responses of coatings with different thicknesses were calculated. The distributions of shear stress and von Mises stress were investigated, respectively.
The magnitude contours of Hertzian response of shear stress inside the coating configuration with different thicknesses under the same tribological conditions are shown in Fig.2. It can be seen that when the coating is thin (tc/a=0.5), the location of the maximum shear stress appears in the substrate. When the coating is a little thicker (tc/a=1.0), the location of the maximum shear stress moves from the substrate to the coating, but near the coating/substrate interface. When the coating is much thicker (tc/a=2.0 or 4.0), the locations of the maximum shear stress both remain in the coating and are obviously far from the coating/substrate interface. However, whether the coating is thin or thick, the location of the maximum shear stress occurs beneath the edge of contact region, that is, x=a. The shear stress distributions of coatings with different thicknesses along y-axis at x=a are shown in Fig.3. It can be seen that for all coatings, there exists a stress discontinuity at the coating/substrate interface, whereas there is not an obvious relationship between the magnitude of the maximum shear stress and the coating thickness.
The magnitude contours of Hertzian response of von Mises stress in the coating with different thicknesses under the same tribological conditions are shown in Fig.4. It can be seen that for all coatings, the locations of the maximum von Mises stress are all on the surface of coatings and just at the contact center. When the coating is relative thin (tc/a=0.5, 1.0 or 2.0), although the maximum von Mises stress occurs on the surface, the magnitudes of von Mises stress at the coating/substrate interfaces are comparatively high. Whereas, when the coating is thick enough (tc/a=4.0), the von Mises stress at interface clearly decreases. The von Mises stress distributions in coatings with different thicknesses along
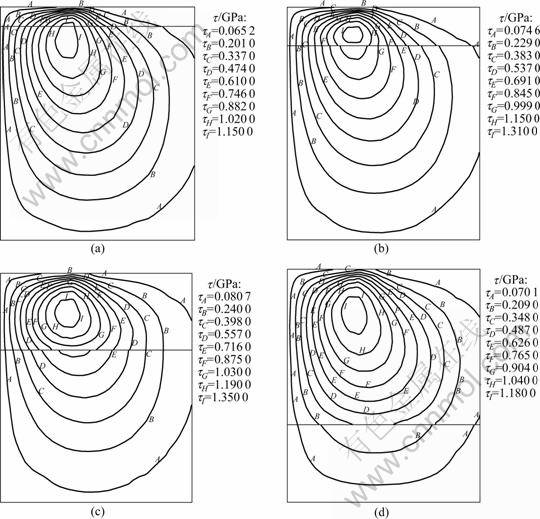
Fig.2 Magnitude contours of shear stress in coatings with different thicknesses subjected to the same loading condition: (a) tc/a= 0.5; (b) tc/a=1.0; (c) tc/a=2.0; (d) tc/a=4.0
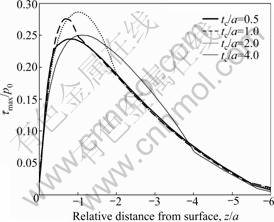
Fig.3 Shear stress distributions along y-axis at x=a for coatings with different thicknesses (where z is distance from surface to tested point)
y-axis at x=0 are shown in Fig.5. It can be seen that the magnitudes of the maximum von Mises stress decrease as the thickness of coating increases. For all coating configurations, there is also discontinuity of the von Mises stress at the coating/substrate interface.
3.2 Stress distributions of coatings with different elastic moduli
Hertzian contact responses of coatings with different elastic moduli were calculated. The distributions of shear stress and von Mises stress were also investigated.
The magnitude contours of Hertzian response of shear stress in coatings with different elastic moduli under the same loading conditions are shown in Fig.6. It can be seen that for all coatings, the locations of the maximum shear stress all appear in coatings at almost the same depths (distance from the surface). The shear stress distributions in coatings with different elastic moduli along y-axis at x=a are shown in Fig.7. It can be obviously seen that the coating with higher ratio is subjected to the more intensive maximum shear stress, although the interface of the coating with higher elastic modulus ratio bears weaker shear stress.

Fig.4 Magnitude contours of von Mises stress in coatings with different thicknesses subjected to the same loading condition: (a) tc/a= 0.5; (b) tc/a=1.0; (c) tc/a=2.0; (d) tc/a=4.0

Fig.5 von Mises stress distributions along y-axis at x=0 for coatings with different thicknesses
The magnitude contours of Hertzian response of von Mises stress in coatings with different elastic moduli under the same loading conditions are shown in Fig.8. It can been seen that for all coatings, the locations of the maximum von Mises stress are all just at the contact center, that is, x=0. And for the coating with low elastic modulus ratio (Ec/Es=0.5), there is only one region subjected to intensive von Mises stress in the coating, which is just near the contact region. For the coatings with higher ratios (Ec/Es=2.0, 4.0 or 8.0), there are two regions subjected to the intensive stress, which are the portions near the contact region and the coating/substrate interface, respectively. The von Mises stress distributions in coatings with different elastic moduli along y-axis at x=0 are shown in Fig.9. It is obvious that high elastic modulus ratio can remarkably increase the magnitude of the maximum von Mises stress at the contact center and the interface, respectively.
4 DiscussionIt is well known that stresses (shear stress and von Mises stress) in coatings are important factors that cause the failure of sprayed-coatings in the rolling contact applications [20-21]. The shear stress is usually recognized as a key driver for controlling the spalling

Fig.6 Magnitude contours of shear stress in coatings with different elastic moduli subjected to the same loading condition: (a) Ec/Es= 0.5; (b) Ec/Es=2.0; (c) Ec/Es=4.0; (d) Ec/Es=8.0

Fig.7 Shear stress distributions along y-axis at x=a for coatings with different elastic moduli
and delamination of coatings. Some results showed that sometimes the depth of cohesive delamination that represents the delamination from the inside of coating is in accordance with that of the maximum shear stress in the coating. At the same time, the adhesive delamination of sprayed-coating, which represents the delamination from the coating/substrate interface, also usually occurs under the rolling contact. For this catastrophic failure, the shear stress at the interface is recognized as a key parameter, owing to accelerating the interface crack initiation and propagation. As the low bond strength of coating and substrate is the inevitable defect of sprayed-coating, decreasing the maximum and interface shear stress may be effective approach to resist RCF. The calculation results show that the effect of thickness on the magnitude of the maximum shear stress is uncertain, but the effect on the interface shear stress is obvious. The interfaces of the thin coatings (tc/a=0.5 or 1.0) are subjected to intensive shear stress. On the contrary, the interfaces of the thick coatings (tc/a=2.0 or 4.0) bear weak stress as the location of the maximum shear stress moves away from the interface. In this case, the crack initiation and propagation are both suppressed. So, the thicker sprayed-coating can perform better fatigue- resistant property. Elastic modulus can also obviously influence the magnitude and distribution of the shear stress in the coating. For the coating with high elastic modulus ratio (Ec/Es=4.0 or 8.0), there is remarkable
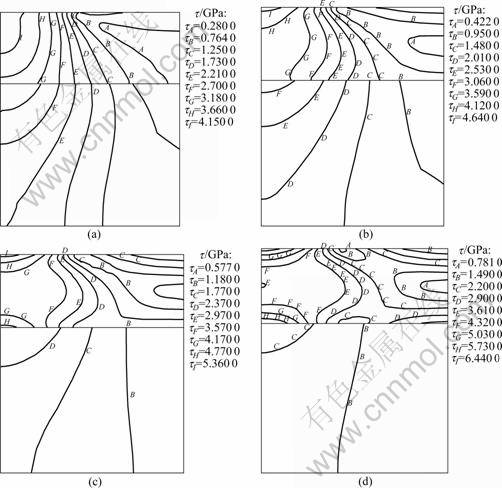
Fig.8 Magnitude contours of von Mises stress in coatings with different elastic moduli subjected to the same loading condition: (a) Ec/Es=0.5; (b) Ec/Es=2.0; (c) Ec/Es=4.0; (d) Ec/Es=8.0
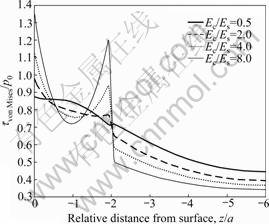
Fig.9 von Mises stress distributions along y-axis at x=0 for coatings with different elastic moduli
stress discontinuity (high maximum shear stress and low interface shear stress), which may be caused by the clear difference of material mechanical properties. On the contrary, the coating with the low elastic modulus ratio (Ec/Es=0.5 or 2.0) shows comparatively smooth transition on the stress curve. So, the low elastic modulus ratio may be beneficial to fatigue-resistance.
The von Mises stress is recognized as a key parameter for controlling the initiation of surface micro-crack resulting in the surface abrasion and the wear caused by plastic yield [22-23]. The calculation results show that magnitudes of the maximum von Mises stress and interface stress of thick coatings are both comparatively low. The status of stress concentration and plastic yield in thick coatings may be slight under the identical loading condition, so, the thick coatings exhibit better fatigue-resistant property, although there is also slight stress discontinuity at the interface of thick coating. The coating with high elastic modulus ratio (Ec/Es=4.0 or 8.0) is obviously subjected to the intensive maximum von Mises stress, interface stress and stress discontinuity. This can be also attributed to the response of different material properties. When the coatings and substrate exhibit obviously different mechanic properties, the interface inevitably bears intensive stress concentration, which drives the micro-defects at the interface to be fatigue cracks and finally results in the fracture. The coating with low modulus ratio (Ec/Es=0.5 or 2.0) performs smooth stress curve, which implies that the similar mechanical properties between the coating and the substrate optimize the stress distribution and promote the RCF resistant performance.
5 Conclusions(1) The stress distribution of the sprayed-coating under pure rolling contact is analyzed by FEM. The effects of thickness and elastic modulus on the Hertzian contact response in the single-layer sprayed-coatings are investigated.
(2) The thickness of coatings plays an important role in the distribution and magnitude of the stress in the sprayed-coating under rolling contact. Although the magnitudes of the maximum shear stress are irregular for coatings with different thicknesses, the interface shear stress of the thick coating is obviously weaker compared with that of the thin coating. For the von Mises stress, the stress intensity in the thick coating also decreases clearly. So, the thicker coating is of excellent RCF resistance.
(3) The elastic modulus ratio of the coating to the substrate also influences the behavior of the stress condition. The low magnitude of the maximum shear stress and the smooth shear stress distribution curves are obtained in the coating with lower elastic modulus ratio. For von Mises stress, the coating with higher modulus ratio is also subjected to severely high maximum stress, interface stress and stress discontinuity. So, comparatively low elastic modulus ratio of the coating to the substrate is beneficial to resisting RCF.
References[1] ZHANG Xian-chang, XU Bin-shi, XUAN Fu-zhen, TU Shan-dong, WANG Hai-dou, WU Yi-xiong. Fatigue resistance of plasma- sprayed CrC-NiCr cermet coatings in rolling contact [J]. Appl Surf Sci, 2008, 254(13): 3734-3744.
[2] STEWART S, AHMED R, ITSUKAICHI T. Contact fatigue failure evaluation of post-treated WC-NiCrBSi functionally graded thermal spray coatings [J]. Wear, 2004, 257(9/10): 962-983.
[3] NAKAJIMA A, MAWATARI T, YOSHIDA M, TANI K, NAKAHIRA A. Effects of coating thickness and slip ratio on durability of thermally sprayed WC cermet coating in rolling/sliding contact [J]. Wear, 2000, 241(2): 166-173.
[4] REN Z, GLODEZ S, FAJDIGA G, UIBIN M. Surface initiated crack growth simulation in moving lubricated contact [J]. Theor Appl Fract Mech, 2002, 38(2): 141-149.
[5] STEWART S, AHMED R. Rolling contact fatigue of surface coatings: A review [J]. Wear, 2002, 253(11/12): 1132-1144.
[6] WEI Yang, JAING Bai-ling, SHI Hui-ying, XIAN Lin-yun. Effects of KMnO4 on microstructure and corrosion resistance of microarc oxidation coatings on 2024 aluminum alloy [J]. Journal of Central South University of Technology, 2010, 17(2): 223-227.
[7] PIAO Zhong-yu, XU Bin-shi, WANG Hai-dou, PU Chun-huan. Investigation of rolling contact fatigue lives of Fe-Cr alloy coatings under different loading condition [J]. Surf Coat Technol, 2010, 204(9/10): 1450-1411.
[8] AHMED R. Contact fatigue failure modes of HVOF coatings [J]. Wear, 2002, 253(3): 473-487.
[9] LIU Hong-xi, TANG Bao-yin, WANG Lang-ping, WANG Xiao-feng, JIANG Bo. Fatigue life and mechanical behaviors of bearing steel by nitrogen plasma immersion ion implantation [J]. Surf Coat Technol, 2007, 201(9/11): 5273-5277.
[10] FUJII M, MA J B, YOSHIDA A, SHIGEMURA S, TANI K. Influence of coating thickness on rolling contact fatigue of alumina ceramics thermally sprayed on steel roller [J]. Tribol Int, 2006, 39(11): 1447-1453.
[11] FAGAN M J, PARK S J, WANG L. Finite element analysis of the contact stresses in diamond coatings subjected to a uniform normal load [J]. Diamond Relat Mater, 2000, 9(1): 26-36.
[12] DIAO D F, SAWAKI Y, SUZUKI H. Effect of interlayer on maximum contact stresses of hard coating under sliding contact [J]. Surf Coat Technol, 1996, 86/87(2): 480-485.
[13] DIAO D F, KATO K. Spalling mechanism of Al2O3 ceramic coatings coated WC-Co substrate under sliding contact [J]. Thin Solid Films, 1994, 245(1/2): 104-108.
[14] ZHANG Xian-cheng, XU Bin-shi, WANG Hai-dou, WU Yi-xiong, JIANG Yi. Hertzian contact response of single-layer, functionally graded and sandwich coatings [J]. Mater Des, 2007, 28(1): 47-54.
[15] SAIZONOU C, KOUITAT-NJIWA R, von STEBUT J. Surface engineering with functionally graded coatings: A numerical study based on the boundary element method [J]. Surf Coat Technol, 2002, 153(2/3): 290-297.
[16] CIAVARELLA M, MONNO F, DEMELIO G. On the Dang Van fatigue limit in rolling contact fatigue [J]. Int J Fatigue, 2006, 28: 852-863.
[17] MORROW C, LOVELL M. Numerical contact analysis of transversely isotropic coatings [J]. Wear, 1999, 236(1/2): 360-367.
[18] HERTZ H. On the contact of elastic solids [J]. J Reine Angew Math, 1882, 92: 156-171.
[19] JOHNSON K L. Contact mechanics [M]. Cambridge: Cambridge University Press, 1992: 11-12.
[20] STEWART S, AHMED R. Contact fatigue failure modes in hot isostatically pressed WC-12%Co coatings [J]. Surf Coat Technol, 2003, 172(2/3): 204-216.
[21] FUJII M, YOSHIDA A, MA J B, SHIGEMURA S, TANI K. Rolling contact fatigue of alumina ceramics sprayed on steel roller under pure rolling contact condition [J]. Tribol Int, 2006, 39(9): 856-862.
[22] ZHANG Xian-chang, XU Bin-shi, XUAN Fu-zhen, TU Shan-dong, WANG Hai-dou, WU Yi-xiong. Fatigue resistance and failure mechanisms of plasma-sprayed CrC-NiCr cermet coatings in rolling contact [J]. Int J Fatigue, 2009, 31(5): 906-915.
[23] ZHANG Xian-chang, XU Bin-shi, XUAN Fu-zhen, TU Shan-dong, WANG Hai-dou, WU Yi-xiong. Rolling contact fatigue behavior of plasma-sprayed CrC-NiCr cermet coatings [J]. Wear, 2008, 265(11/12): 1875-1883.
Foundation item: Project(2007AA04Z408) supported by the National High-Tech Research and Development Program of China; Project(50735006) supported by the National Natural Science Foundation of China
Received date: 2009-11-20; Accepted date: 2010-03-08
Corresponding author: WANG Hai-dou, Professor; Tel: +86-10-66718541; E-mail: wanghaidou@tsinghua.org.cn

