
J. Cent. South Univ. (2020) 27: 221-230
DOI: https://doi.org/10.1007/s11771-020-4290-5

3D stability assessment of stepped slopes in inhomogeneous soils
LI Xiong-wei(李雄威)1, ZHU Jian-qun(朱建群)1, LI Zheng-wei(李正伟)2, YANG Xiao-li(杨小礼)2
1. Department of Civil & Architecture Engineering, Changzhou Institute of Technology, Changzhou 213032, China;
2. School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Stability assessment of slopes has historically been performed assuming soils to be homogeneous in two-dimensional (2D) cases. In real cases, soils are usually inhomogeneous, and each slope collapse indicates a three-dimensional (3D) nature. Based on a 3D rotational failure mechanism, this work develops an approach to account for the impact of the vertical strength inhomogeneity on the 3D stability of stepped slopes. Seismic actions are taken into account by introducing the concept of a horizontal seismic coefficient. An upper-bound expression for stability factors is derived in the light of the kinematic approach, and the most critical solution is obtained from an optimization programming. In comparison with the previously published solutions, the validity of the proposed method is shown. A sensitivity analysis is carried out to discuss parametric effects on the stability of 3D stepped inhomogeneous slopes.
Key words: inhomogeneous soil; stepped slope; stability factor; 3D horn failure mechanism
Cite this article as: LI Xiong-wei, ZHU Jian-qun, LI Zheng-wei, YANG Xiao-li. 3D stability assessment of stepped slopes in inhomogeneous soils [J]. Journal of Central South University, 2020, 27(1): 221-230. DOI: https://doi.org/ 10.1007/s11771-020-4290-5.
1 Introduction
Stability analysis of slopes has received significant attention in the literature [1-3]. Prior work is mainly concentrated on 2D plane strain mechanisms, yet the stability analyses under 3D conditions are relatively rare. All failures of slopes are 3D in nature, implying the need to derive a 3D solution. The available approaches for 3D slope stability analysis can be roughly divided into three main classes: 1) limit equilibrium; 2) numerical simulations; and 3) limit analysis. UGAI and LESHCHINSKY [4] developed a limit equilibrium- based finite method for predicting 3D slope stability. CHEN et al [5] constructed a compatible failure mechanism and obtained the safety factor from the energy-work balance equation in the framework of the upper-bound theorem. GRIFFITHS and MARQUEZ [6] demonstrated several 3D slope stability examples by the finite element method and validated the results against conventional 2D analyses. CAMARGO et al [7] utilized a numerical limit analysis-based finite element method to deal with 3D slope stability problems in catchment areas. Using the kinematic approach, MICHALOWSKI and DRESCHER [8] presented a 3D rotational mechanism to estimate the stability of a single-stage slope. This method was subsequently extensively applied in engineering [9-12]. The focus of these published analyses was mainly on 3D single-stage slopes in homogenous soils.
Soils are commonly treated as a kind of homogeneous material in geotechnical engineering. In practice, due to internal and external environmental factors, soils usually show the characteristics of observable inhomogeneity. Some efforts have been made to investigate the influence of strength inhomogeneity. An empirical formula was developed to calculate the bearing capacity of inhomogeneous clay foundation. CHEN [13] summarized some types of strength inhomogeneity distribution and developed a 2D approach to analyze the impact of the vertical inhomogeneity on the slope stability. DAVIS and BOOKER [14] obtained the solution to the problem of bearing capacity of inhomogeneous clay by means of the theory of plasticity. GOURVENEC and RANDOLPH [15] used the finite element method to estimate bearing capacity of foundations resting on clays with different degrees of strength inhomogeneity. NIAN et al [16] studied the stability of slopes reinforced with piles in inhomogeneous soils using the kinematic approach. LIU and KOYI [17] investigated the effect of the dip, location and thickness of a weak horizon on the stability of inhomogeneous granular slopes. These contributions were mainly limited to the 2D slope stability or foundation bearing capacity in inhomogeneous soils.
Limit analysis is a useful approach in practical engineering [18-20]. Stepped slopes are commonly used. There exists a question how to assess the stability of 3D stepped inhomogeneous slopes. The present work adopts a 3D collapse mechanism to calculate the stability of 3D stepped inhomogeneous slopes using the kinematic approach. The soils are assumed to be vertically inhomogeneous only. A quasi-static approach by introducing the concept of a horizontal seismic coefficient is employed to replace earthquake actions. An upper-bound expression for the stability factors is derived. In order to validate the present method, a comparison with the results of MICHALOWSKI and DRESCHER [8] is carried out. This paper ends with a discussion on parametric effects of different affecting factors.
2 Strength inhomogeneity of soils
The inhomogeneity of soils is primarily caused by the varying depositional environments. It is known that soil cohesion increases along the depth. As shown by CHEN [13], several different forms of cohesion distribution along the depth were published previously. In this paper, as typically assumed, the cohesion of soils increases linearly along the depth from n0c at the top to c at the toe of slope (n0, inhomogeneity coefficient; c, cohesion).Figure 1 illustrates the cohesion distribution in stepped slopes along the depth diagrammatically. Therefore, the cohesion, ci, at depth below the top surface, h, takes the form as
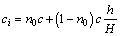 (1)
(1)
From Eq. (1), it is obvious to see that the soils will be homogeneous when n0=1.0.

Figure 1 3D horn failure mechanism for stepped slopes in inhomogeneous soils
3 Kinematical solution to stability of 3D stepped slopes
3.1 3D failure mechanism for stepped slopes
A stepped slope in inhomogeneous soils is studied in the present work. The geometry of the slope is shown in Figure 1. The total height of the slope is H, with α1H and α2H for the upper and lower portions respectively, where α1 and α2 are depth coefficients. Namely,
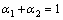 (2)
(2)
For dimensionless operation, a new parameter λa termed step width coefficient is introduced to represent the step width a, defined as λa=a/H.
The kinematic approach is a powerful tool to investigate geotechnical stability problems [21-25]. It states that for a valid collapse mechanism, the results obtained from the principle of virtue work are rigorous upper bounds on the true solution. The flow rule leads to a condition where the angle of the velocity vector and the sliding surface corresponds to the internal fiction angle φ.
This section is to describe the 3D horn failure mechanism proposed by MICHALOWSKI and DRESCHER [8]. As shown in Figure 1, the mechanism can be determined by two log-spirals, i.e., curve AE
 (3)
(3)
and curve A′E′
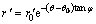 (4)
(4)
with r0=OA, r′0=OA′, and θ0 depicted in Figure 1. The mechanism is generated by revolving a circle with varying radius. Thus, all cross sections of the mechanism are circular. The trace of the circle center rm and the circle radius R are determined as follows:
 (5)
(5)
 (6)
(6)
with f1 and f2 listed in Appendix.
Referring to MICHALOWSKI and DRESCHER [8], a plane strain block is included in the mechanism, as described in Figure 2, to ensure that the present solution is equal to the solution of plane strain mechanisms when the slope width reaches infinity. The width of the inserted block can be expressed as
 (7)
(7)
where B is the width of slope and B′max is the maximum width of 3D portion. Therefore, if the geometry of stepped slope and properties of soil mass are provided, the mechanism can be defined using three variables: angles θ0 and θh, and ratio r′0/r0.
For the calculations, a local coordinate system is built in each cross section (see Figure 1). Therefore, the velocity v about axis O reads
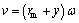 (8)
(8)
where 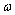 is the rotational angular velocity.
is the rotational angular velocity.
3.2 Calculations of internal energy dissipation rate
The formula for dissipation rate D along the sliding surface St can be written as follows:
 (9)
(9)
With the above formula, the rate of dissipation for the 3D portion is derived as:


 (10)
(10)
with g1 and g2 given in Appendix, and di (i=1, 2, 3, 4) are the function of θ, whose expressions can be found easily from Figure 1 as follows:
 (11)
(11)

Figure 2 Schematic diagram of 3D mechanism:
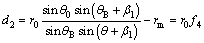 (12)
(12)
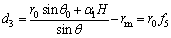 (13)
(13)
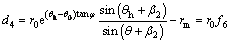 (14)
(14)
where f3-f6 are dimensionless functions given in Appendix. Angles θB, θC and θD can determined by trigonometric relations in Figure 1, which are
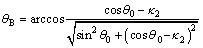 (15)
(15)

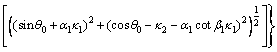 (16)
(16)


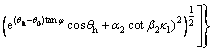 (17)
(17)
where κ1=H/r0 and κ2=L/r0, as given in Appendix, with L = AB. Owing to the complexity of the 3D mechanism, the integration over θ given in Eq. (10) can be only performed in a numerical way. Regarding the inserted portion, the rate of internal dissipation holds:
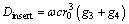 (18)
(18)
with g3 and g4 listed in Appendix.
Consequently, the total internal dissipation rate is:
 (19)
(19)
3.3 Calculations of external work rate
For the 3D portion, the external work rate due to the soil weight is deduced as:
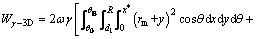
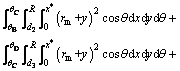

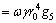 (20)
(20)
with g5 given in Appendix. Similarly, for the inserted portion, the external work rate of the soil weight is derived as:
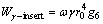 (21)
(21)
with g6 listed in Appendix.
The seismic action is considered by introducing the concept of a horizontal seismic coefficient  [26, 27]. Therefore, the work rate due to the seismic force is formulated as
[26, 27]. Therefore, the work rate due to the seismic force is formulated as

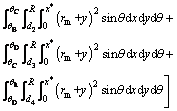
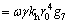 (22)
(22)
with g7 listed in Appendix. For the inserted portion, the work rate of the seismic force can be written as
 (23)
(23)
with g8 given in Appendix.
The rate of total external work is determined by
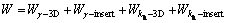
 (24)
(24)
3.4 Derivation of stability factor
An expression about the critical height Hcr can be derived from D=W, which can be written as the following formula:
 (25)
(25)
In order to make sure that the horn failure mechanism is geometrically meaningful, the following constraint conditions are required
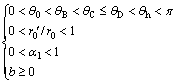 (26)
(26)
According to the kinematic approach, the lowest upper-bound solution among all possible results is required, which is obtained from an optimization scheme.
The stability factor Ns of slopes in inhomogeneous soils is typically defined as
 (27)
(27)
4 Numerical results and discussion
4.1 Comparison
A stepped slope is reduced to a single-stage slope when the inclined angles β1=β2 and the step width coefficient λa=0.0. When m0=1.0 and kh=0.0, the inhomogeneity and earthquake effect are not considered. Therefore, the 3D static stability estimation of single-stage slopes in homogeneous soils, which has been considered by MICHALOWSKI and DRESCHER [8], can be regarded as a special case of the proposed method. For validation, a comparison with the results provided by MICHALOWSKI and DRESCHER [8] is carried out corresponding to φ=15°, λa=0.0, n0=1.0, kh=0.0 and β1=β2, as listed in Table 1.
Taking the impact of volume strain into account, MICHALOWSKI and DRESCHER [8] investigated the 3D static stability problem of single-stage uniform slopes. In this work, the strength inhomogeneity means that the value of cohesion is not a constant along the depth. Owing to the difficulty in calculating the internal energy dissipation rate within deforming volume in inhomogeneous soils, the soil mass is assumed to be rigid in the present work. However, from the comparison shown in Table 1, it is seen that the impact of volume strain is relatively low, which can be neglected. This suggests that the proposed approach is feasible.
Table 1 Comparison with MICHALOWSKI and DRESCHER [8]

4.2 Sensitivity analysis
The proposed approach can also be employed to study the parametric effect on the stability of inhomogeneous slops. In order to investigate how the parameters affect the 3D static and seismic stability of stepped slopes in inhomogeneous soils, sets of results are calculated.
Figure 3 shows the impact of the soil inhomogeneity coefficient n0 on the stability factors along the ratio B/H for single-stage slopes (β1=β2=45°, λa=0.0) and stepped slopes (β1=45°, β2=60°, λa=0.2) subjected different seismic conditions. From the results, it is found that increasing n0 will enhance the slope stability.
Figure 4 illustrates the influence of the step width coefficient λa on the stability factors along the ratio B/H and along the inhomogeneity coefficient n0. It can be found that the presence of the step leads to a significant increase of the stability.
Figure 5 illustrates effect of the seismic coefficient kh on the stability factors along the ratio B/H and along the inhomogeneity coefficient n0. It can be observed that earthquake has an adverse effect on the slope stability.
Figure 6 illustrates effect of the inclined angle β1 on the stability factors along the ratio B/H and along the inhomogeneity coefficient n0. It is concluded that the stability factors increase when the inclined angle β1 increases.
In addition, from the results, it is interesting to see that the stability factors decline sharply within the range B/H≤3.0, then, the stability factors decrease lightly with increasing B/H. For instance, in Figure 3(d), at n0=0.7, the stability factors decrease by 42.0% from 12.661 to 7.343 by increasing B/H from 0.8 to 3.0; however, the stability factors only decrease by 10.5% with B/H arising from 3.0 to 10.0. This suggests that it is necessary to consider the 3D effect when the ratio B/H is small. The 3D effect is less obvious with the increase of ratio B/H.

Figure 3 Effect of inhomogeneity coefficient n0 on stability factors:

Figure 4 Effect of step width coefficient λa on stability factors:
5 Conclusions
The present study aims to develop an approach for the 3D stability estimation of stepped slopes in inhomogeneous soils. An upper-bound expression for stability factors is derived by using the kinematic approach of limit analysis. The lowest upper-bound results for different parameters are sought by an optimization programming. To validate the present approach, the proposed solutions are compared with those of MICHALOWSKI and DRESCHER [8]. It is shown that the approach of this work is effective. The present paper extends the work of MICHALOWSKI and DRESCHER [8] from single-stage slopes to stepped slopes, with considerations of the vertical strength inhomogeneity of soils and earthquake effect.

Figure 5 Effects of seismic coefficient kh on stability factors:
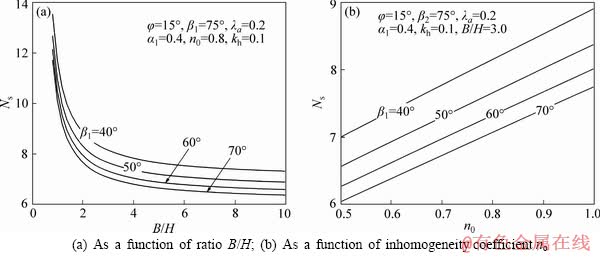
Figure 6 Effects of inclined angle β1 on the stability factors:
The stability assessment of stepped slopes in inhomogeneous soils is of great importance. Based on the obtained results, the impact of several parameters is analyzed. It is concluded that the increase of the inhomogeneity coefficient n0 and the step width coefficient λa has a favorable effect, while the increase of the seismic coefficient and the inclined angle β1 has an opposite effect. Additionally, it can be found that the stability factors decrease as the ratio B/H increases. The 3D effect has great influence on the slope stability, especially in a small value of B/H, and the effect becomes weaker with increasing B/H. After B/H reaches 10.0, the 3D effect is so low that can be neglected.
Appendix
 (A1)
(A1)

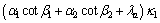 (A2)
(A2)
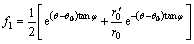 (A3)
(A3)
 (A4)
(A4)
 (A5)
(A5)
 (A6)
(A6)
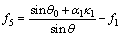 (A7)
(A7)
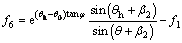 (A8)
(A8)
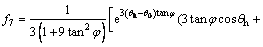
 (A9)
(A9)
 (A10)
(A10)

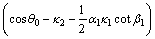 (A11)
(A11)

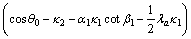 (A12)
(A12)

 (A13)
(A13)

 (A14)
(A14)
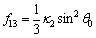 (A15)
(A15)

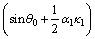 (A16)
(A16)
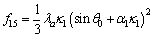 (A17)
(A17)

 (A18)
(A18)

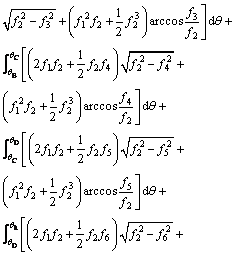
 (A19)
(A19)
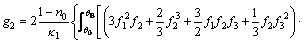

 (A20)
(A20)
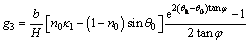 (A21)
(A21)

 (A22)
(A22)
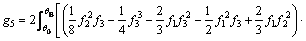


 (A23)
(A23)
 (A24)
(A24)


 (A25)
(A25)
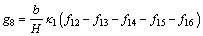 (A26)
(A26)
References
[1] AMINPOUR M M, MALEKI M, GHANBARI A. Investigation of the effect of surcharge on behavior of soil slopes [J]. Geomechanics and Engineering, 2017, 13(4): 653-669.
[2] YANG X L, CHEN J H. Factor of safety of geosynthetic-reinforced slope in unsaturated soils [J]. International Journal of Geomechanics, 2019, 19(6): 04019041.
[3] LI LC, TANG C A, ZHU W C, LIANG Z Z. Numerical analysis of slope stability based on the gravity increase method [J]. Computers and Geotechnics, 2009, 36(7): 1246-1258.
[4] UGAI K, LESHCHINSKY D O V. Three-dimensional limit equilibrium and finite element analyses: A comparison of results [J]. Soils and Foundations, 1995, 35(4): 1-7.
[5] CHEN Z, WANG X, HABERFIELD C, YIN J H, WANG Y. A three-dimensional slope stability analysis method using the upper bound theorem: Part I: Theory and methods [J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 369-378.
[6] GRIFFITHS D V, MARQUEZ R M. Three-dimensional slope stability analysis by elasto-plastic finite elements [J]. Géotechnique, 2007, 57(6): 537-546.
[7] CAMARGO J, VELLOSO R Q, VARGAS E A. Numerical limit analysis of three-dimensional slope stability problems in catchment areas [J]. Acta Geotechnica, 2016, 11(6): 1369-1383.
[8] MICHALOWSKI R L, DRESCHER A. Three-dimensional stability of slopes and excavations [J]. Géotechnique, 2009, 59(10): 839-850.
[9] Li Z W, Yang X L, Li T Z. Static and seismic stability assessment of 3D slopes with cracks [J]. Engineering Geology, 2020, 265: 105450.
[10] Huang F, Zhang M, Wang F, Ling T H, Yang X L. The failure mechanism of surrounding rock around an existing shield tunnel induced by an adjacent excavation [J]. Computers and Geotechnics, 2020, 117: 103236.
[11] Li T Z, Yang X L. Stability of plane strain tunnel headings in soils with tensile strength cut-off [J]. Tunnelling and Underground Space Technology, 2020, 95: 103138.
[12] Zhong J H, Yang X L. Kinematic stability of tunnel face in non-uniform soils [J]. KSCE Journal of Civil Engineering, 2020, 24(2). DOI: 10.1007/s12205-020-0996-z.
[13] CHEN W F. Limit analysis and soil plasticity [M]. Elsevier Science, Rotterdam, the Netherlands, 1975.
[14] DAVIS E H, BOOKER J R. The effect of increasing strength with depth on the bearing capacity of clays [J]. Géotechnique, 1985, 23(4): 551-563.
[15] GOURVENEC S, RANDOLPH M. Effect of strength non-homogeneity on the shape of failure envelopes for combined loading of strip and circular footings on clay [J]. Géotechnique, 2003, 53(6): 575-586.
[16] NIAN T K, CHEN G Q, LUAN M T, YANG Q, ZHENG D F. Limit analysis of the stability of slopes reinforced with piles against landslide in nonhomogeneous and anisotropic soils [J]. Canadian Geotechnical Journal, 2008, 45(8):1092-1103.
[17] LIU Z, KOYI H A. Analogue modeling of the collapse of non-homogeneous granular slopes along weak horizons [J]. Tectonophysics, 2014, 632: 76-95.
[18] Shi G C, Chen G, Pan Y T, Yang X L, Liu Y, Dai G Z. Stress-drop effect on brittleness evaluation of rock materials [J]. Journal of Central South University, 2019, 26(7): 1807-1819.
[19] Yang X L, Zhong J H. Stability analysis of tunnel face in nonlinear soil under seepage flow[J]. KSCE Journal of Civil Engineering, 2019, 23(10): 4553-4563.
[20] LI Y X, YANG X L. Seismic displacement of 3D slope reinforced by piles with nonlinear failure criterion [J]. International Journal of Geomechanics, 2019, 19(6): 04019042.
[21] Li T Z, Yang X L. Probabilistic analysis for face stability of tunnels in Hoek-Brown media [J]. Geomechanics and Engineering, 2019, 18(6): 595-603.
[22] ZhouZ,GaoWY,LiuZZ,ZhangCC.Influencezonedivisionandriskassessmentofunderwatertunneladjacentconstructions[J].MathematicalProblemsinEngineering, 2019, (3):1-10.
[23] ZHOUZ,XINGK,YANGH,WANGH.Damagemechanismofsoil-rockmixtureafterfreeze-thawcycles[J].JournalofCentralSouthUniversity, 2019, 26(1): 13-24.
[24] Xu J S, Du X L, Yang X L. Stability analysis of 3D geosynthetic-reinforced earth structures composed of nonhomogeneous cohesive backfills [J]. Soil Dynamics and Earthquake Engineering, 2019, 126: 105768.
[25] Huang F,Feng Y,Zhang Z Q,Yang X L, Ling T H. Upper bound solution of the safety factor for a shield tunnel face subjected to the Hoek-Brown failure criterion [J]. International Journal of Civil Engineering, 2019, 17(12): 1941-1950.
[26] MONONOBE N, MATSUO H. On the determination of earth pressures during earthquakes [J]. Proceedings of World Engineering Congress, 1929, 9: 179-187.
[27] OKABE S. General theory on earth pressure and seismic stability of retaining wall and dam [J]. Journal of Japan Society of Civil Engineers, 1924, 10(6): 1277-1323.
(Edited by HE Yun-bin)
中文导读
非均质土中台阶边坡的三维稳定性分析
摘要:传统的边坡分析一般是在二维情况下进行的,并且假设土壤是均匀的。在实际情况下,土壤通常是不均匀的,而且边坡崩塌都显示出三维的性质。本文基于三维旋转破坏机理,提出了考虑垂直强度不均匀性对台阶边坡三维稳定性影响的方法。同时引入水平地震系数的概念来考虑地震作用。根据上限定理导出了稳定因子的表达式,并通过优化规划得到了最优解。通过与已有解的比较,证明了该方法的有效性。最后,对三维台阶非均质边坡稳定性进行了敏感性分析,讨论了参数对边坡稳定性的影响。
关键词:非均质土;台阶边坡;稳定系数;三维旋转破坏机理
Foundation item: Project(51378510) supported by the National Natural Science Foundation of China
Received date: 2018-04-05; Accepted date: 2019-05-16
Corresponding author: LI Zheng-wei, PhD Candidate; Tel: +86-13080564647; E-mail: lizhengwei@csu.edu.cn; ORCID: 0000-0003- 3884-4893