J. Cent. South Univ. (2012) 19: 1558-1563
DOI: 10.1007/s11771-012-1176-1
Clock-based RAIM method and its application in GPS receiver positioning
TENG Yun-long(滕云龙)1, 2, SHI Yi-bing(师奕兵)1
1. School of Automation Engineering, University of Electronic Science and Technology of China, Chengdu 611731, China;
2. Research Institute of Electronic Science and Technology,
University of Electronic Science and Technology of China, Chengdu 611731, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Because the signals of global positioning system (GPS) satellites are susceptible to obstructions in urban environment with many high buildings around, the number of GPS useful satellites is usually less than six. In this case, the receiver autonomous integrity monitoring (RAIM) method cannot exclude faulty satellite. In order to improve the performance of RAIM method and obtain the reliable positioning results with five satellites, the series of receiver clock bias (RCB) is regarded as one useful satellite and used to aid RAIM method. From the point of nonlinear series, a grey-Markov model for predicting the RCB series based on grey theory and Markov chain is presented. And then the model is used for aiding RAIM method in order to exclude faulty satellite. Experimental results demonstrate that the prediction model is fit for predicting the RCB series, and with the clock-based RAIM method the faulty satellite can be correctly excluded and the positioning precision of GPS receiver can be improved for the case where there are only five useful satellites.
Key words: positioning precision; receiver autonomous integrity monitoring (RAIM); receiver clock bias (RCB); grey theory; Markov chain
1 Introduction
Nowadays, global positioning system (GPS) plays an important part in vehicle navigation and positioning [1-5]. In order to improve the positioning precision, receiver autonomous integrity monitoring (RAIM) method has been widely used in GPS receivers [6-9]. The RAIM method involves two functions. The first one is to detect whether faulty satellite exists or not. The second one is to identify which satellite is malfunctioning and excludes the faulty one. Normally, the function of fault exclusion of the RAIM method needs at least six satellites.
However, in certain applications, for example in urban environment with many high buildings around, there are situations wherein the requirement of a minimum of six satellites is not satisfied because of the obstructions to receiver-to-satellite line of sights. In the circumstances, RAIM method cannot exclude faulty satellite anymore. To solve this problem, additional devices such as the inertial navigation system (INS) [10] and pseudolite [11] can be introduced into GPS receiver to aid RAIM method. It is also possible to increase the number of satellites by combining GPS and Galileo [12]. The above mentioned methods may be useful, but not efficient. In fact, the cost of these methods has great impact on their popularizations. To decrease the cost, it is desired to develop a method through the inner information from GPS receivers.
Actually, besides the position information of GPS receivers, the receiver clock bias (RCB) is obtained when the function of positioning calculation is implemented normally. When the clock frequency of GPS receiver keeps stable, the RCB series can be regarded as one useful satellite [13], and a prediction model about it can be used for aiding RAIM method. Compared with other auxiliary methods, the clock-based RAIM method needs no external equipments.
In fact, there are many complicated factors which have an impact on the RCB series, including the atmosphere and ionosphere delays, and the orbital errors of GPS satellites. Influenced by these factors, the RCB series can be considered as nonlinear time series. From the point of nonlinear series, the grey-Markov model for predicting the RCB series based on grey theory and Markov chain is presented. With the aid of the prediction model, the clock-based RAIM method used for positioning calculation is developed.
2 Grey-Markov prediction model
The combined prediction model in this work consists of grey theory and Markov chain. Grey theory is suitable for such kinds of nonlinear series with few data and little fluctuation, and Markov chain has good ability to describe nonlinear series of the random fluctuations and predict the possible change on the nonlinear series by probabilistic transform matrixes. By combining their advantages, the grey-Markov prediction model takes advantage of grey theory to reflect the development tendency of the RCB series, while the Markov chain is utilized to predict the fluctuation along the tendency.
2.1 GM(1,1) model
Grey prediction is an important component of the grey theory, and traditional GM(1,1) model is widely used [14]. The mathematical expression of GM(1,1) will be presented.
1) Accumulated generating operation (AGO)
The aim of this step is to transform the original time series into a new AGO series which is characterized by less noise and randomness. Set the RCB series as
{c(t)}=[c(1), c(2), …, c(M)] (1)
The equation used for generating the AGO series is given by
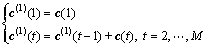(2)
2) First-order differential equation
The GM(1,1) model can be constructed through establishing a first-order differential equation for the AGO series as
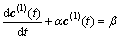(3)
where parameter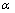 
is called the development parameter, standing for the development tendency of the AGO series. Parameter 
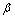is the coordination parameter, which tells us the transformation relations between the original series and the AGO series.
3) Parameters calculation
The parameters can be calculated by
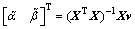(4)
where
(5)
4) Prediction equation for GM(1,1)
This step is dedicated to calculate the predicted values for the AGO series. The equation used is
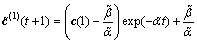(6)
5) Inverse accumulated generating operation (IAGO)
The operation is brought to calculate the inverse of AGO. It is utilized to transform the forecasted AGO series back to the original series. It is achieved by using the following equations:
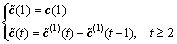(7)
And the residual errors are defined as
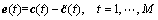(8)
2.2 Markov chain prediction
In this section, the residual errors in Eq. (8) will be modified by means of using the Markov chain. Before determining states for Markov transition matrix, the residual errors are partitioned into K regions called states. In the grey-Markov prediction model, K=3. When K is selected as 3, it is indicated that the current state should be moved forward, backward, or stay unchanged [15]. Let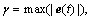
then the three states are determined as
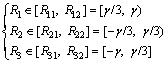(9)
With these states, the state transition probability from Ri to Rj after one step is given by:
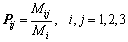(10)
where Mij is the number of state transitions from Ri to Rj, and Mi=Mi1+Mi2+Mi3.
Let vi (i=1, 2, 3) denote the centers of the three states. Suppose that the residual error e(t) locates at Ri in the current step. Then the predicted RCB value for the next step is
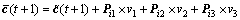(11)
Compared with the RCB series, the predicted error is given by
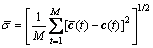(12)
3 Clock-based RAIM method for GPS positioning
3.1 Expansion of measurement equation
Let N represent the number of GPS satellites. The measurement equation used can be written as
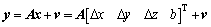(13)
where 
is the pseudo-range measurement vector;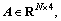 
denotes the measurement matrix; 
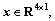denotes the estimated vector including three correction parameters relative to the true position of GPS receiver and the RCB value; 
is the zero-mean measurement noise vector with a standard deviation of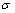 
for all useful satellites.
When the RCB prediction model is used for aiding RAIM method, Eq. (14) should be introduced into Eq. (13):
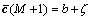(14)
where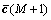 
denotes the predicted RCB value, and it can be obtained from Eq. (11). In the clock-based RAIM method, the measurement errors (v) and the predicted errors (ζ) are required to be independent and obey the same distributions, so Eq. (14) should be transformed as
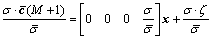(15)
By substituting Eq. (15) into Eq. (13), the expanded measurement equation is obtained by
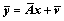(16)
where
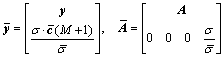(17)
3.2 Fault detection and exclusion
After the expanded measurement equation has been obtained, the parity vector used in the clock-based RAIM method which contains the error information of faulty satellite can be defined as
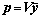(18)
where V is the parity matrix satisfying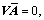 
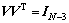, and it can be obtained from the QR- decomposition method.
The parity vector contains the error information of faulty satellite, which can be used for judging whether faulty satellite exists or not. Define SD=pTp as the detection statistics, and it will be compared with the detection threshold TD to judge whether faulty satellite exists or not. If SDD, there is no faulty satellite. Otherwise, faulty satellite exists.
The threshold is related with the number of useful satellites, the probability of false alarm (p) and the noise in the pseudo-range measurements (σ). In the absence of faulty satellite, SD/σ2 obeys the chi-square distribution whose freedom degree is N-3. Supposing that f(x) is the probability density function which follows chi-square distribution with N-3 degrees of freedom, the detection threshold can be given by
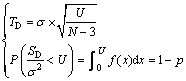(19)
If faulty satellite exists, it is necessary to find out which satellite is unhealthy and the information about this satellite will be eliminated. Assuming Vi respects the corresponding column vector of the parity matrix, the statistic for determining faulty satellite can be obtained as
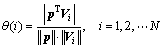(20)
In order to exclude the faulty satellite, the statistic is carried out for every satellite. The satellite which has the largest statistic is considered as the faulty one.
3.3 Positioning calculation
As soon as the faulty satellite has been identified, the information about it must be excluded from the measurement equation. And then the other satellites are used for positioning calculation in order to provide uninterrupted and reliable positioning results. Based on the above mentioned procedures, Fig. 1 illustrates the flowchart of the clock-based RAIM method used for positioning calculation.
4 Experiments and results
The experiments were conducted to demonstrate the validity of the presented method in predicting the RCB series and improving the positioning precision. During the experiments, sudden fault and soft fault with GPS satellite are considered, respectively, and there are five useful satellites. Additionally, the noise in the pseudo- range measurements (σ) and the probability of false alarm (p) are set as 10 m and 10-4, respectively.
4.1 Performance under sudden fault
4.1.1 Prediction of RCB series
The RCB series used are illustrated in Fig. 2. It can be seen that the RCB values are comparatively large. If the grey-Markov prediction model is used for predicting the RCB series directly, it will increase the complexity greatly and mass data have to be saved. Aiming at this problem, the grey-Markov model is used for predicting the first-order difference series instead of the series themselves, which can reduce the calculation complexity and improve the prediction precision. Figure 2 illustrates the predicted errors of the RCB series.
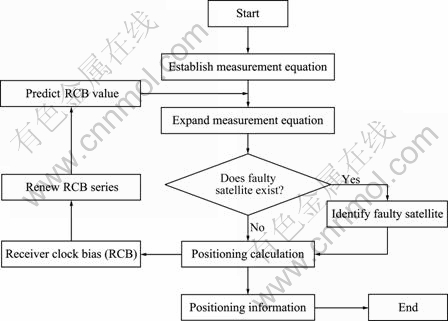
Fig. 1 Flowchart of clock-based RAIM method
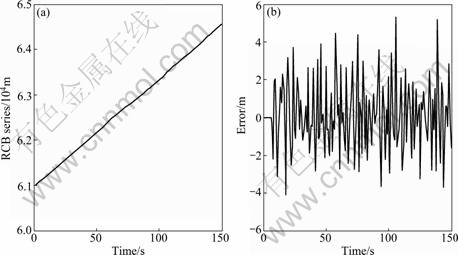
Fig. 2 RCB series (a) and predicted errors (b)
It is observed that the maximum in the predicted errors is less than 6 m. Figure 2 also shows that the presented model not only gives a good fit to the RCB series but also predicts its future behavior well. That is to say, the grey-Markov prediction model is reasonable and feasible to predict the RCB series.
4.1.2 Analysis of positioning results
To demonstrate the performance of the clock-based RAIM method under sudden fault, the fault was added to the pseudo-range of a certain satellite and it was considered as the faulty one. The value of added fault is 100 m, and it lasts from 61 s to 90 s. The RAIM and clock-based RAIM method are used to exclude faulty satellite, and then the other satellites are utilized for positioning calculation. Figure 3 illustrates the positioning errors provided by two methods above. In Fig. 3, CRAIM is short for the clock-based RAIM method.
Figure 3 shows that the positioning errors of GPS receiver brought out by the RAIM method are close to 150 m, and they are outside the range of normal positioning precision. The reason of this phenomenon is that the fault exclusion function of RAIM method requires at least six satellites, hence the faulty satellite cannot be excluded under the conditions of five useful satellites. Accordingly, the faulty satellite exists during the course of positioning calculation.
While the positioning errors obtained from the CRAIM method are less than 6 m and in bounds of normal precision. Because the RCB prediction model based on grey theory and Markov chain is equivalent to one useful satellite, the clock-based RAIM method aiding of the prediction model can exclude the faulty satellite when there are only five satellites. In the circumstances, the positioning precision using the other satellites has been improved effectively.
4.2 Performance under soft fault
The positioning performance using the clock-based RAIM method under soft fault will be discussed in this section. We add fault to the pseudo-range of a certain satellite and consider this satellite as the faulty one. The value of added fault starts at 10 m from 120 s, and its step is 10 m. Similar to Section 4.1, the RAIM and CRAIM method are utilized to exclude the faulty satellite, and then the other satellites are used for positioning calculation, respectively. The positioning errors are shown in Fig. 4.
Figure 4 indicates that the positioning errors provided by the RAIM method increases rapidly from 121 s, and it even exceeds 400 m at 150 s. Accordingly, these results can not be used for positioning anymore. While the positioning errors by using the CRAIM method increases gradually only between 121 s and 130 s. That is because the detection statistics increases with the increment of the added fault from 121 s and exceeds the detection threshold at 131 s. In the circumstance, the CRAIM method can exclude the faulty satellite correctly, so that the positioning results using the other satellites become reliable and reasonable again. This is the fundamental reason that the positioning errors are less than 5 m from 131 s.
From the experiments in this section, we can come to a conclusion that the grey-Markov model is suitable for predicting the RCB series, and the clock-based RAIM method for positioning calculation is effective and feasible. Equipped with the clock-based method, the function of fault exclusion of the RAIM method can be realized and the positioning precision of GPS receiver can be ensured, even if there are only five useful satellites. Moreover, the methodology presented in this work does not need extra equipments, and it’s much more feasible and effective.
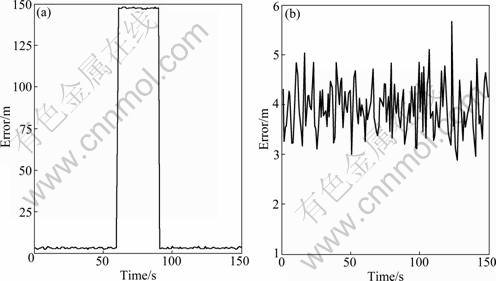
Fig. 3 Positioning errors under sudden fault: (a) RAIM; (b) CRAIM
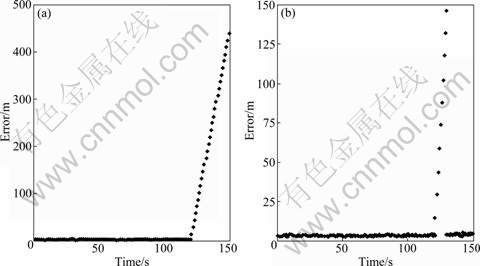
Fig. 4 Positioning errors under soft fault: (a) RAIM; (b) CRAIM
5 Conclusions
1) The grey-Markov model for predicting the RCB series is presented. The prediction model is utilized to exclude faulty satellite by means of aiding RAIM method under five useful satellites. The experiments show the validity and feasibility of the method.
2) The positioning precision of GPS receiver through the clock-based RAIM method depends on the prediction performance of the RCB series. How to improve on the prediction model of the RCB series is an important issue worthy of further research.
References
[1] HU Hai-dong, HUANG Xian-lin, LI Ming-ming, SONG Zhuo-yue. Federated unscented particle filtering algorithm for SINS/CNS/GPS system [J]. Journal of Central South University of Technology, 2010, 17(4): 778-785.
[2] ZHANG Jian-jun, YUAN Hong. Analysis of unmanned aerial vehicle navigation and height control system based on GPS [J]. Journal of Systems Engineering and Electronics, 2010, 21(4): 643-649.
[3] CHEN Yu-bo, SONG Ying-chun. A Bayes filter algorithm with non-Gaussian noises based on location of vehicular GPS [J]. Journal of Central South University: Science and Technology, 2010, 41(4): 1462-1466. (in Chinese)
[4] TONG Xiao-hua, WU Song-chun, WU Shu-qing, LIU Da-jie. A novel vehicle navigation map matching algorithm based on fuzzy logic and its application [J]. Journal of Central South University of Technology, 2005, 12(2): 214-219.
[5] WU Fu-mei, NIE Jian-liang, HE Zheng-bin. Low-cost GPS/INS integrated navigation algorithm in land vehicle system considering attitude update [J]. Journal of Chinese Inertial Technology, 2010, 18(6): 675-679.(in Chinese)
[6] BLANCH J, WALTER T, ENGE P. RAIM with optimal integrity and continuity allocations under multiple failures [J]. IEEE Trans on Aerospace and Electronic Systems, 2010, 46(3): 1235-1247.
[7] YANG Chuan-sen, XU Xiao-hao, LIU Rui-hua, ZHAO Hong-sheng. New algorithm for receiver autonomous integrity monitoring [J]. Transactions of Nanjing University of Aeronautics & Astronautics, 2010, 27(2): 155-161.
[8] WANG Jin-ling, OBER P B. On the availability of fault detection and exclusion in GNSS receiver autonomous integrity monitoring [J]. Journal of Navigation, 2009, 62(2): 251-261.
[9] LIU Wen-xiang, LI Zheng-rong, WANG Fei-xue. A new RAIM method for detecting and correcting weak pseudo-range bias under gradual change [J]. Journal of Astronautics, 2011, 31(4): 1024-1029.(in Chinese)
[10] HEWITSON S, WANG Jin-ling. Extended receiver autonomous integrity monitoring (eRAIM) for GNSS/INS integration [J]. Journal of Surveying Engineering, 2010, 136(1): 13-22.
[11] GUO Rui, ZHANG Jian-ting, FENG Lai-ping, YANG Zhen. Analysis of RAIM availability and its performance under pseudolite-aided condition [J]. Progress in Astronomy, 2009, 27(1): 89-97. (in Chinese)
[12] LEE Y C. Investigation of extending receiver autonomous integrity monitoring (RAIM) to combined use of Galileo and modernized GPS [C]// Proceedings of the 17th International Technical Meeting of the Satellite Division of the Institute of Navigation. Long Beach, USA, 2004: 1691-1698.
[13] BEDNARZ S, MISRA P. Receiver clock-based integrity monitoring for GPS precision approaches [J]. IEEE Trans on Aerospace and Electronic Systems, 2006, 42(2): 636-642.
[14] FOULY E L, SAADANY E L, SALAMA M M. Grey predictor for wind energy conversion systems output power prediction [J]. IEEE Trans on Power Systems, 2006, 21(3): 1450-1452.
[15] SU S F, LIN C B, HSU Y T. A high precision global prediction approach based on local prediction approaches [J]. IEEE Trans on Systems, Man and Cybernetic, 2002, 32(4): 416-425.
(Edited by DENG Lü-xiang)
Foundation item: Project(20090580013) supported by the Aeronautic Science Foundation of China; Project(ZYGX2010J119) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2011-03-24; Accepted date: 2011-06-22
Corresponding author: TENG Yun-long, PhD; Tel: +86-28-61831176; E-mail: tyluestc@163.com
