- Abstract:
- 1 Introduction▲
- 2 Non-local constitu...▲
- 3 Mathematical formu...▲
- 4 Propagation of wav...▲
- 5 Reflection of P-wa...▲
- 6 Numerical results ...▲
- 7 Conclusions▲
- References
- Figure
- Figure 1 Geometry of problem
- Figure 2 Effect of fractional order parameter on speed of waves versus angular frequency in medium for ε=0.1
- Figure 3 Effect of fractional order parameter on reflection coefficients |Zj| (j=1, 2, 3, 4, 5) with respect to angle of incidence for nonlocal (ε=0.1) medium with voids
- Figure 4 Reflection coefficients |Zj| (j=1, 2, 3, 4, 5) versus angle of incidence for local (ε=0) and nonlocal (ε=0.2, 0.3) parameter

J. Cent. South Univ. (2020) 27: 3188-3201
DOI: https://doi.org/10.1007/s11771-020-4472-1
Reflection of thermo-elastic wave in semiconductor nanostructures nonlocal porous medium
HASHMAT Ali1, ADNAN Jahangir2, AFTAB Khan1
1. Department of Mathematics, COMSATS University Islamabad, Islamabad Campus 44000, Pakistan;
2. Department of Mathematics, COMSATS University Islamabad, Wah Campus 47040, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract:
The current work is an extension of the nonlocal elasticity theory to fractional order thermo-elasticity in semiconducting nanostructure medium with voids. The analysis is made on the reflection phenomena in context of three-phase-lag thermo-elastic model. It is observed that, four-coupled longitudinal waves and an independent shear vertical wave exist in the medium which is dispersive in nature. It is seen that longitudinal waves are damped, and shear wave is un-damped when angular frequency is less than the cut-off frequency. The voids, thermal and non-local parameter affect the dilatational waves whereas shear wave is only depending upon non-local parameter. It is found that reflection coefficients are affected by nonlocal and fractional order parameters. Reflection coefficients are calculated analytically and computed numerically for a material, silicon and discussed graphically in details. The results for local (classical) theory are obtained as a special case. The study may be useful in semiconductor nanostructure, geology and seismology in addition to semiconductor nanostructure devices.
Key words:
Cite this article as:
HASHMAT Ali, ADNAN Jahangir, AFTAB Khan. Reflection of thermo-elastic wave in semiconductor nanostructures nonlocal porous medium [J]. Journal of Central South University, 2020, 27(11): 3188-3201.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-020-4472-11 Introduction
Eringen’s [1] nonlocal elasticity theory is the most widely used theory and different nonclassical thermoelasticity theories have been developed with some extra atomistic features based on Eringen’s [1] theory. The nonlocal theory [1] supposed that the involvement of strain field at the neighboring points about any local point is also very significant in the study of stress applied at that particular point in the solid continuum. Therefore, the nonlocal elasticity theory has area of study for atoms or molecules containing long-range forces, thus, an internal length scale parameter is needed to formulate the problem.
ALTAN [2] proved the uniqueness theorem of linear nonlocal elasticity theory. CHIRITA [3] solved some boundary value problems using the idea of nonlocal theory of elasticity. CRACIUN [4] presented his model under the effect of nonlocal thermoelasticity. The nonlocal elasticity models characterized by the presence of nonlocality residuals of fields (like body force, mass, entropy, internal energy, etc.) have been proposed by EDELEN et al [5, 6]. ERINGEN et al [7-10] used the non-local theory to different other areas.
IESAN [11] first introduced voids in the local theory of coupled thermo-elasticity. He presented that the propagation of shear vertical wave was not affected by thermal and voids parameters. A number of researchers applied the concept of Iesan’s model [11] to contribute their efforts in this field. Recently, SING et al [12] investigated the effects of voids on the waves propagating through nonlocal elastic solid. The applications background of generalized thermo-elasticity theory containing voids have been studied in the literatures [13-18]. BACHHER et al [19] discussed nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer. BISWAS et al [20] presented propagation of waves under the dual-phase-lag model. Recently, SARKAR et al [21] analyzed the effect of voids and nonlocal parameter on propagation of plane waves in the context of generalized thermo-elasticity theory [11].
Many real life problems of heat conduction models have been solved by using the concept of fractional calculus in last two decades. POVSTENKO [22] fruitfully formulated fractional order time derivative Fourier law of heat conduction by using the definition of CAPUTO [23] time fractional derivative in classical Fourier law of heat conduction. SHERIEF et al [24] discussed the special cases of fractional thermoelasticity theory for weak and strong conductivity. YOUSSEF [25] studied the fractional generalized thermoelasticity theory by taking into consideration fractional order heat conduction model. EZZAT et al [26] discussed the magnetic effects on the thermal elastic waves under the supposition of fractional order heat transfer model and also in Ref. [27] they discussed the fractional order theory in thermo-elastic solid with three- phase lag heat transfer. HAMZA et al [28, 29] formulated the two relaxation times fractional theory of thermo-elasticity and they also solved a problem of one-dimensional in the Cartesian and spherical coordinate systems to prove the uniqueness of the theory. IBRAHIM [30] studied generalized thermo elastic interaction in functional graded material with fractional order three-phase lag heat transfer.
SONG et al [31] discussed the reflection of photo-thermal waves in a semiconducting medium under generalized thermo-elastic theory. TANG et al [32] considered the reflection of waves in semiconductor nanostructures. IBRAHIM et al [33] studied the dual phase lag model of photo thermal interaction in a semiconductor material. Recently, JAHANGIR et al [34] investigated the reflection phenomena of waves in a semiconductor nanostructure elasticity medium and ALI et al [35] studied reflection of waves in a rotating semiconductor nanostructure medium through torsion-free boundary condition.
Porous materials have extensive applications in aerospace, electronic communications, construction, metallurgy, nuclear energy, petrochemical, mechanical, medical, and environmental protection due to their advantageous properties, such as low relative density, high specific strength and surface area, lightweight, thermal and acoustical insulation, and good permeability. A subject of current technological interest is in of nanotechnology. Nonlocal continuum mechanics could potentially play a useful role in analysis related to nanotechnology applications. The length scales associated with nanotechnology are often sufficiently small to call the applicability of classical continuum models into question. Atomic and molecular models, while certainly conceptually valid for small length scales, are difficult to formulate accurately and are almost always computationally intensive. Nonlocal continuum models represent attempts to extend the continuum approach to smaller length scales while retaining most of its many advantages.
In the current work, reflection of waves in semi-conducting nanostructures medium with voids is discussed. The nonlocal fractional order thermo- elasticity theory is applied to studying the propagation of waves in semiconductors nanostructures. It is observed that five plane waves, which are dispersive in nature, are propagating through the semi-conducting medium with voids. The medium generates the four coupled longitudinal and an independent shear vertical waves. The coupled longitudinal waves are affected by the non-local, thermal and voids parameters in the medium, but the shear vertical wave is depending only upon the nonlocal parameter. The absolute values of speed of waves and reflection coefficients are solved analytically. The results are computed for a particular semi-conducting material silicon and explained through graphs in details. The obtained results are discussed as special cases to make the comparisons of local and nonlocal theories of elasticity.
2 Non-local constitutive relations
Some basic relations according to Eringen’s [1] theory of nonlocal elasticity for thermo-elastic medium with voids [36] are listed as follows:
In the following relations, the quantities having superscript “L” represents the local medium.
Local-nonlocal stress relation:
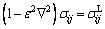 (1)
(1)
Local stress-displacement-strain-carrier density function relation:
 (2)
(2)
Volume fraction field-elastic parameter relation:
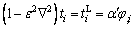 (3)
(3)
Volume fraction field-elastic parameter- constants-temperature relation:
 (4)
(4)
Local-nonlocal entropy-temperature-strain-
volume fraction field relation:
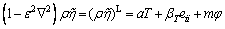 (5)
(5)
Strain-displacement relation:
 (6)
(6)
In nonlocal theory of nanostructured semiconductor thermo-elastic solid with voids, equations of motion are expressed by:
 (7)
(7)
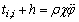 (8)
(8)
where δij is the Kronecker delta; 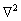 is the Laplacian operator;
is the Laplacian operator; 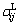 is the Cauchy’ stress tensor at the local point; ρ is the bulk density of the medium; ui is the displacement vector and χ (new elastic constant) is the equilibrated inertia.The partial derivative with respect to space coordinates is represented by a comma ‘,’ occurring in the subscript; superimposed dot characterizes the partial derivative with respect to time; λ and μ are Lame elastic constants; φ is so-called volume fraction field; υ and τ′ are new elastic constants; γ and α′ are elastic parameters and m is called thermo-voids parameter.
is the Cauchy’ stress tensor at the local point; ρ is the bulk density of the medium; ui is the displacement vector and χ (new elastic constant) is the equilibrated inertia.The partial derivative with respect to space coordinates is represented by a comma ‘,’ occurring in the subscript; superimposed dot characterizes the partial derivative with respect to time; λ and μ are Lame elastic constants; φ is so-called volume fraction field; υ and τ′ are new elastic constants; γ and α′ are elastic parameters and m is called thermo-voids parameter.
The particular conditions on various material parameters as discussed by COWIN et al [37] are expressed as follows:
μ≥0, α′≥0, υ≥0, 3λ+2μ≥0, (3λ+2μ)υ≥3γ2
Following IESAN [11], BACHHER et al [38] and CHALLAMEL et al [39], here, we presented the Cattaneo type [19] three-phase-lag thermo- elastic model given by HAMZA et al [29] based on Eringen-type differential model for the generalized nonlocal elasticity theory of fractional order for thermo-elastic material with voids as follows:
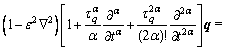
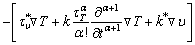 (9)
(9)
where 0<α≤1, In the above heat conduction model, q is representing the heat flux vector; The quantities τq, τT and τυ represent the phase lags of the heat flux, the temperature gradient and the thermal displacement, respectively. In the context of the thermo-elasticity theory, the energy equation for a homogenous isotropic thermo-elastic solid (in absence of heat source) is given by HAMZA et al [29].
In the above heat conduction model, q is representing the heat flux vector; The quantities τq, τT and τυ represent the phase lags of the heat flux, the temperature gradient and the thermal displacement, respectively. In the context of the thermo-elasticity theory, the energy equation for a homogenous isotropic thermo-elastic solid (in absence of heat source) is given by HAMZA et al [29].
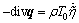 (10)
(10)
where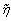 and T0 denote the entropy and ambient temperature of the medium, respectively.
and T0 denote the entropy and ambient temperature of the medium, respectively.
3 Mathematical formulation
Consider the medium as semiconducting nanostructures-homogeneous isotropic thermoelastic material with porosity. Introducing the relations expressed in Eqs. (1)-(6), in Eqs. (7)- (10) and by considering TANG et al [32], the governing equations for propagation of the waves in the considered medium are expressed as follows:

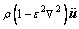 (11)
(11)
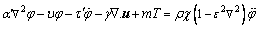 (12)
(12)
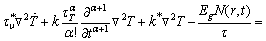
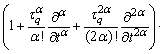
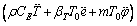 (13)
(13)
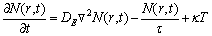 (14)
(14)
where aT0=ρCE and the plasma diffusion Eq. (14) governing the plasma transportation process in semiconductors nanostructure medium with voids is barrowed from Ref. [31]. e=ui,ji, N(r, t) is a carrier density; T(r, t) is the temperature; r stands for position vector; DE is carrier diffusion coefficients; τ photo-generated carrier lifetime; CE and k are coefficients of specific heat and thermal conductivity, respectively; Eg is energy gap of the semiconductor parameter; βT=(3λ+2μ)αT is the volume thermal expansion. αT is the coefficients of linear thermal expansion. δn=(3λ+2μ)dn and dn is coefficients of electronic deformation.
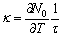 is coupling parameter for thermal activation and N0 is carrier concentration at equilibrium position.
is coupling parameter for thermal activation and N0 is carrier concentration at equilibrium position.
The Helmholtz vector decomposition technique is introduced in scalar potential function f and vector potential function ψ as follows:
 (15)
(15)
Considering xz-plane of propagation,by employing relations expressed in Eq. (15),Eqs. (11)-(14) are transformed to potentials form as follows:
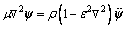 (16)
(16)
 (17)
(17)
 (18)
(18)
 (19)
(19)
 (20)
(20)
Following set of dimensionless variables are used to:
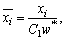
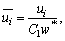
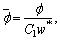
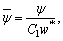
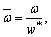
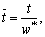


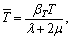

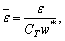

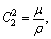
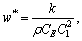

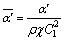
The following system of non-dimensional equations is obtained after employing the above variables to Eqs. (16)-(20) (for simplicity omitting the bar sign).
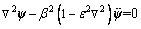 (21)
(21)
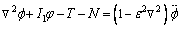 (22)
(22)
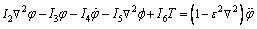 (23)
(23)
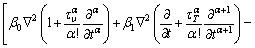
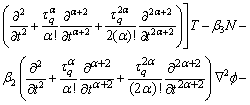
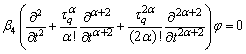 (24)
(24)
 (25)
(25)
It is obvious from Eqs. (22)-(25) that the variables φ, T and N are coupled with the longitudinal component f of the displacement vector u, resulting in generation of four coupled longitudinal waves. It can also be observed that Eq. (21) is un-coupled in potential ψ. The necessary condition 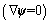 of the Helmholtz vector decomposition implies that:
of the Helmholtz vector decomposition implies that:
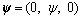 (26)
(26)
Opting Eq. (26), from Eq. (21), we have
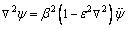 (27)
(27)
Hence, we examine that the propagation of SV-type wave remains unaffected by the thermal effect and porosity. These results are the same in the case of semi-conducting nanostructure medium under nonlocal theory of thermo-elasticity and classical theory of elasticity. The expression (27) shows that the shear vertical wave is only influenced by the nonlocality in the medium.
4 Propagation of waves
Let us assume that the medium of the propagation be the nonlocal semi-conducting nanostructure with voids such that angle of propagation is θ with the normal direction. Let V be the speed of propagation of the waves in the medium. The proposed harmonic wave solution of different potentials can take the form as follows:
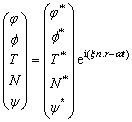 (28)
(28)
where n=(n1, n3) such that (n1)2+(n3)2=1 is propagation vector; ξ is the wave number; 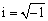 is the imaginary number, ω is the angular frequency; r is the position vector and f*, ψ*, T* and N* are constant amplitudes of the waves. The wave number ξ and speed of waves V have the well- known relation with angular frequency ω such that ω=ξV. System of Eqs. (22)-(25) becomes:
is the imaginary number, ω is the angular frequency; r is the position vector and f*, ψ*, T* and N* are constant amplitudes of the waves. The wave number ξ and speed of waves V have the well- known relation with angular frequency ω such that ω=ξV. System of Eqs. (22)-(25) becomes:
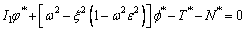 (29)
(29)
 (30)
(30)
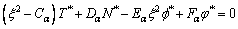 (31)
(31)
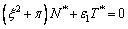 (32)
(32)
where
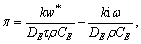

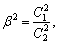
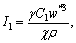
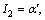
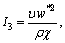
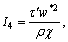 I5=
I5=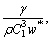
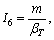
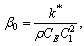


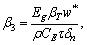
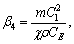
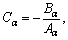
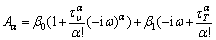
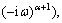
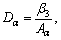
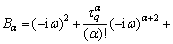
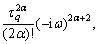
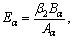
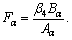
To obtain the non-trivial solution of Eq. (29)- (32), the determinant of coefficients vanishes which implies following secular equation:
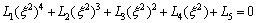 (33)
(33)
where,
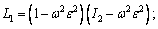
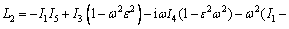
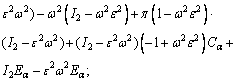
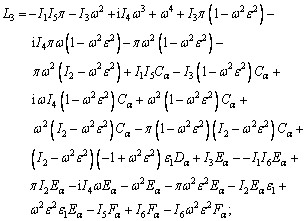
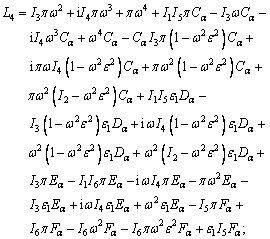
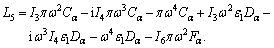
The speeds of coupled longitudinal waves propagating in the semi-conducting nanostructure medium with voids can be calculated by dispersion relation given through Eq. (33) which has complex coefficients; therefore, it will give total four roots in ξ2 such that ±ξj, j=1, 2, 3, 4. It indicates that, there exist eight reflected waves, among which four are along the positive z-axis and remaining four have negative projection along z-axis. Let ξ1, ξ2, ξ3 and ξ4 be corresponding with the positive projection, and let 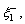
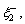
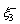 and
and 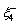 along the negative projection along z axis. From set of Eqs. (22)-(25), it can be analyzed that the waves generated are coupled in nature. The four positive roots will generate four elastic coupled longitudinal waves. The waves propagating with speed V1, V2, V3 and V4 are coupled longitudinal wave (P-wave), coupled thermal wave (T-wave), coupled density carrier wave (LDC-wave) and V-wave (due to voids), respectively.
along the negative projection along z axis. From set of Eqs. (22)-(25), it can be analyzed that the waves generated are coupled in nature. The four positive roots will generate four elastic coupled longitudinal waves. The waves propagating with speed V1, V2, V3 and V4 are coupled longitudinal wave (P-wave), coupled thermal wave (T-wave), coupled density carrier wave (LDC-wave) and V-wave (due to voids), respectively.
Next, plugging the expression of ψ from Eq. (28) into Eq. (27), the speed of transverse waves in non-local thermoelastic semi-conducting isotropic medium with voids is expressed as follows:
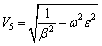 (34)
(34)
The above expression indicates that the speed of shear vertical wave in non-local elasticity theory with voids is real for a particular real value of ω lying in the range 0<ω<ωc and the wave is no more a travelling wave when ω=ωc, where, 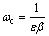 is called the cut-off frequency of the transverse wave.
is called the cut-off frequency of the transverse wave.
The speed of transverse wave given in Eq. (34) can be reduced to classical speed for ε→0, which is in good agreement with the results obtained by SONG et al [31]. The results are acceptable because speed of transverse wave does not depend on the heat conduction model (weather 3PHL or Song’ heat model).
It is clear from Eq. (34) that the non-local theory causes the speed of the SV-type wave to slow down in the thermo-elastic semi-conducting material. This is due to the fact that the strength of the non-local stresses is weaker as compared to that of classical stresses. The non-local stress is also acting upon the neighbourhood points of the local point, thus producing a weak deformation in the solid body.The increase in non-locality in the medium tends to decrease the speed of transverse wave in the range of 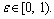
4.1 Nature of speed of waves
The relations (15) and (28) show that the particles associated with the potential f are moving parallel with the direction of wave propagation. Since the potential functions φ, T and N are mutually coupled with the potential f as given in Eqs. (29)-(32), the waves travelling with speeds Vj (j=1, 2, 3, 4) are all longitudinal in nature. The potential ψ in Eq. (28) being the vertical component of the displacement vector u produces the shear vertical wave because its direction becomes normal to propagation vector. We can also express the transverse speed into following formula through Eq. (16),
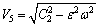 (35)
(35)
where 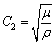 is the speed of classical transverse wave. This expression indicates that wave will exist only if C2>εω and the speed of nonlocal transverse wave decreases by increasing the angular frequency. Further if we let ε=0.1, C2=104, ω=x, and V5=y, then the expression (35) becomes:
is the speed of classical transverse wave. This expression indicates that wave will exist only if C2>εω and the speed of nonlocal transverse wave decreases by increasing the angular frequency. Further if we let ε=0.1, C2=104, ω=x, and V5=y, then the expression (35) becomes:
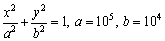
which is an ellipse. It is observed that transverse wave is dispersive as it is depending upon the angular frequency ω. It is nondispersive in the absence of nonlocality of the medium.
4.2 Special cases
The following is some important results which can be deduced from our study:
4.2.1 Non-local thermo elastic semiconductor nanostructure material (without voids)
In the absence of voids, the results of non-local thermo elastic semiconductor nanostructure material, as recently investigated by JAHANGIR et al [34] are obtained by substituting β4=I1= I2=I3=I4=I5=I6=0 in Eq. (33), and then we get a cubic equation as follows:
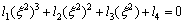 (36)
(36)
where

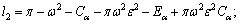
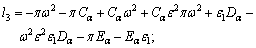
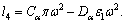
Equation (36) gives the speed of three coupled quasi longitudinal type waves in medium, while the speed of transverse wave is given in Eq. (34).
4.2.2 Non-local elastic isotropic solid (in the absence of thermal and voids)
If we ignore voids as well as the thermal effects and assume that the medium is now isotropic, i.e., substituting 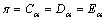 =0 in Eq. (33), then
=0 in Eq. (33), then
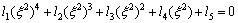 (37)
(37)
where 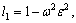
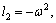
 .
.
So that Eq. (37) becomes
 (38)
(38)
Equation (38) gives the speed of longitudinal wave, i.e., 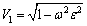 and V2=V3=0, whereas the speed of transverse wave remains the same as expressed in Eq. (34). Hence only two elastic waves propagate as longitudinal and transverse waves in nonlocal isotropic medium. The mathematical expressions of speeds of propagation of both the waves represent that the nonlocal effects reduce the magnitudes of the speeds. It is also noticeable that the longitudinal wave only travels as real wave if the angular frequency satisfies the inequality
and V2=V3=0, whereas the speed of transverse wave remains the same as expressed in Eq. (34). Hence only two elastic waves propagate as longitudinal and transverse waves in nonlocal isotropic medium. The mathematical expressions of speeds of propagation of both the waves represent that the nonlocal effects reduce the magnitudes of the speeds. It is also noticeable that the longitudinal wave only travels as real wave if the angular frequency satisfies the inequality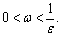
5 Reflection of P-wave
We consider the reflection of an incident coupled longitudinal displacement wave (P-wave), which is incident on the surface of semiconductor nanostructure medium with angle θ. In response to the incident wave, four coupled longitudinal waves such as longitudinal displacement wave (P-wave), thermal wave (T-wave) and carrier density wave (LDC-wave), wave due to voids (V-wave) and one shear vertical wave (SV-wave) propagate through the medium, as shown in Figure 1. Let the longitudinal components of displacement f*, T* and N* for incident and reflected waves are taken in following form:
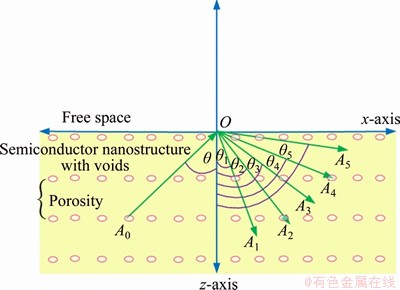
Figure 1 Geometry of problem
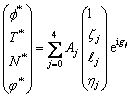 (39)
(39)
and for transverse component of displacement ψ*, we have
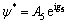 (40)
(40)
where
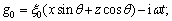
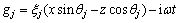 ;
;
 ;
;
whereas ζj, ηj and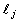 are the coupling parameters of thermal, voids and carrier density waves with the incident coupled longitudinal displacement wave, respectively, through Eqs. (29)–(31), and are given by the following expressions:
are the coupling parameters of thermal, voids and carrier density waves with the incident coupled longitudinal displacement wave, respectively, through Eqs. (29)–(31), and are given by the following expressions:
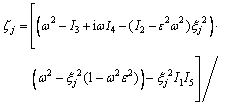
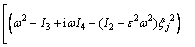
 ;
;
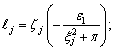
j=0, 1, 2, 3, 4.
The reflection coefficients
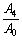 and
and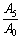 can be determined by imposing the appropriate boundary conditions at the free surface z=0. Let the insulated boundary be free from stresses. This implies that stress components vanish at z=0.
can be determined by imposing the appropriate boundary conditions at the free surface z=0. Let the insulated boundary be free from stresses. This implies that stress components vanish at z=0.
1) Stress free, boundary condition;
2) Isolated, boundary condition;
3) Carrier density, boundary condition;
4) Volume fraction of voids satisfy, boundary condition.
Mathematically, the boundary conditions at z=0 may be expressed as:
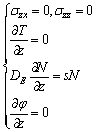 (41)
(41)
where s is the speed of surface re-combination. The boundary conditions presented in Eq. (41) identically satisfy the Snell’s Law, which implies
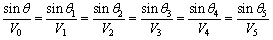 (42)
(42)
Using the expression of f*, T*, N* and ψ* given in Eqs. (39) and (40) in boundary conditions (41) and by using the relation (42), the system of five non-homogeneous equations can be expressed as follows:
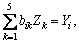 for i=1, 2, 3, 4, 5 (43)
for i=1, 2, 3, 4, 5 (43)
where
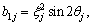
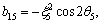
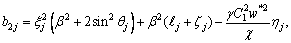
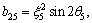
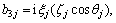 b35=0,
b35=0,
 b45=0,
b45=0,
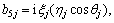 b55=0, Y1=b11, Y2=-b21, Y3=b31,
b55=0, Y1=b11, Y2=-b21, Y3=b31,
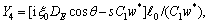 Y5=b51,
Y5=b51,
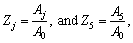 j=1, 2, 3, 4
j=1, 2, 3, 4
where Zj (j=1, 2, 3, 4) are the reflection coefficients of longitudinal displacement wave, thermal wave, longitudinal density carrier wave and the wave due to voids, respectively, whereas Z5 is the reflection coefficient of the transverse wave travelling independently in the medium.
6 Numerical results and discussion
In this section, we discuss the effects of the nonlocal and the fractional order parameters on the speeds and reflection coefficients. For this purpose, we are using the materials constants given by SONG et al [31] as follows:
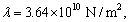
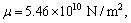
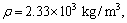
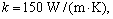
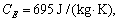
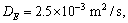
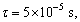
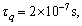
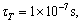
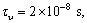
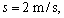

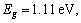

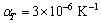 ,
,
and voids parameters are given by [36]
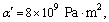
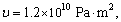

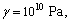
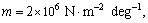
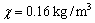 .
.
The graphically representation is given in Figures 2-4. The purpose is to ensure the effects of these parameters on the speeds and on the reflection coefficients, in particular, when a coupled- longitudinal displacement wave is incident on the boundary of the semiconductor nanostructure medium.
6.1 Effect of fractional order parameter on speed of propagation
Figures 2(a)-(e) show the variation of the speed of the waves propagating in the medium versus angular frequency ω. Figure 2(a) shows that the speed (V1) of coupled longitudinal displacement wave has decreasing behaviour and speed of wave increases by increasing α (fractional order parameter). We also examine that the speed is more dispersive for smaller values of α (e.g., α=0.1) and it becomes non-dispersive for α neat to 5. The speed (V2) of coupled thermal wave (T-wave) is the slowest and dispersive in the medium. It is also observed that it is increasing w.r.t α as shown in Figure 2(b). In Figure 2(c), the coupled-carrier density wave propagates in the medium with speed of V3 is dispersive and decreases with the increase in α. Figure 2(d) indicates the variation of speed of the wave (due to voids) versus angular frequency. The speed is increasing by increasing ω and decreasing by increasing α.

Figure 2 Effect of fractional order parameter on speed of waves versus angular frequency in medium for ε=0.1
The speed of propagation of independent shear vertical wave is graphically represented in Figure 2(e) which shows that V5 decreases for increasing values of angular frequency. It is observed that V5→0.61 m/s when ω→0. In fact, when the ω→0, the speed is exactly equal to classical speed and at that point the nonlocality becomes negligible in the medium. It is investigated theoretically that this wave is independent on temperature and hence it is independent on α. For fix amount of non-locality like in our case, i.e. ε=0.1, the speed of transverse wave gives the equation of an ellipse having angular frequency on the minor axis. For the angular frequency 0<ω<5, the wave follows the path of an ellipse, as shown in Figure 2(e).
We observe that all the waves are dispersive in nature since the speeds of all these waves depend upon the angular frequency. These observations are made under the varying strength of the fractional order of thermo-elastic model and at constant values of nonlocal parameter. One can see that wave travelling with speed V1 is the fastest one while the speed of the thermal wave, i.e., V2 is the slowest one. Furthermore, the longitudinal displacement wave with speed V1 is more dispersive but the thermal wave V2 is the least dispersive.
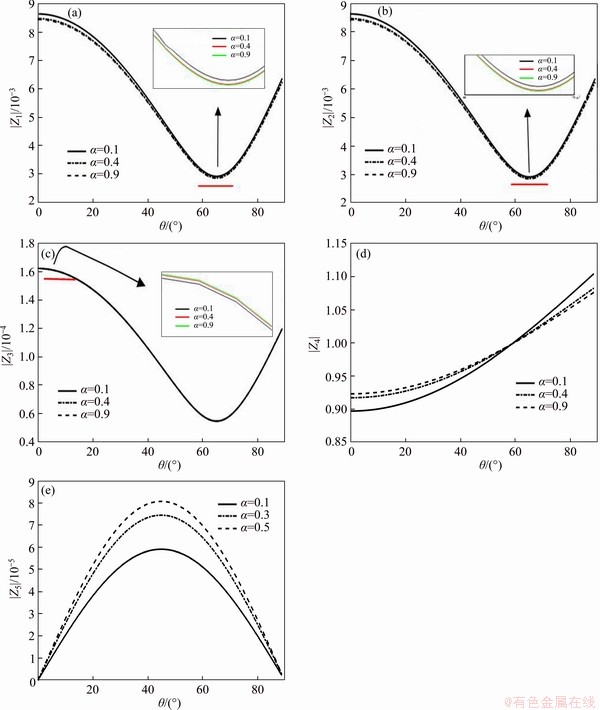
Figure 3 Effect of fractional order parameter on reflection coefficients |Zj| (j=1, 2, 3, 4, 5) with respect to angle of incidence for nonlocal (ε=0.1) medium with voids
6.2 Effect of fractional order parameter on reflection coefficients
In Figures 3(a)-(e), the effect of fractional order time derivative α of the three phase lag thermo-elastic model on the reflection coefficients is shown. Here, the nonlocal stresses act upon the nonlocal point distant at 0.1 nm from the local point of the elastic body. The reflection coefficients Z1 and Z2 are decreasing with increase in α<1 (see Figures 3(a) and (b)) for all angles of incidence. Also it is observed that reflection coefficients Z1 and Z2 have the maximum values when θ→0°and minimum values when θ→65°. The reflection coefficient Z3 of the carrier density wave has almost the same behaviour as in the case of Z1 or Z2 but the fractional order has very minute effect on this reflection coefficient as shown in Figure 3(c). Figure 3(d) indicates the variation of the reflection coefficients Z4 of the wave due to voids. The mixed type behaviour of the reflection coefficients is observed, that is, in the range of the angle of incidence 0°≤θ≤65°, it increases with the increase of α but afterward the reverse effect is detected. Although the shear vertical wave is travelling in the medium as independent of thermal parameter (Eq. (34)), but due to the couple type boundary conditions (Eqs. (41)-(44)), its amplitude becomes coupled. This effect is graphically shown in Figure 3(e), which is a bell shaped curve w.r.t θ and has the maximum value at θ=45°. Also, it is increasing with increase of α.
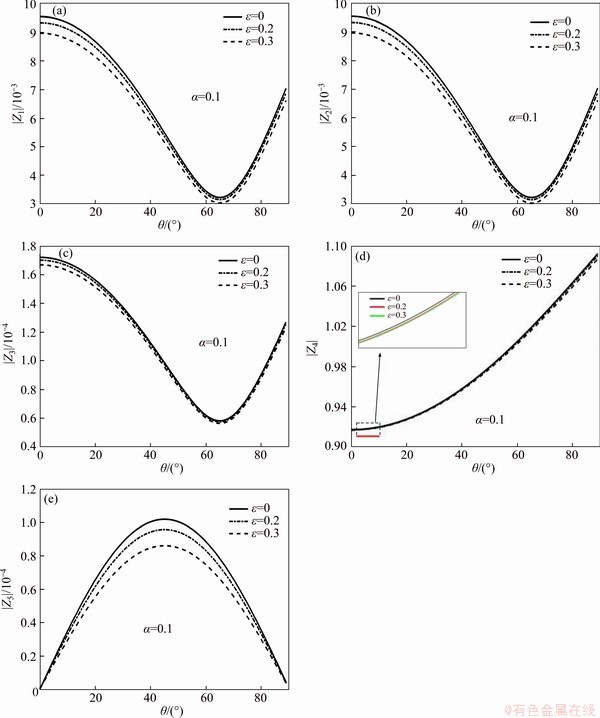
Figure 4 Reflection coefficients |Zj| (j=1, 2, 3, 4, 5) versus angle of incidence for local (ε=0) and nonlocal (ε=0.2, 0.3) parameter
6.3 Effect of non-local parameter on reflection coefficients
The nonlocal parameter ε is made as dimensionless by dividing unit distance d, i.e., 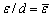 (say). Figures 4(a)-(e) are plotted to study the nature of the reflection coefficients of the reflected waves, namely, the reflected coupled- longitudinal displacement wave, coupled-thermal wave, coupled-carrier density wave, coupled wave due to voids and the independent shear vertical wave respectively. The reflection coefficients |Zj| (j=1, 2, 3, 4, 5) are discussed under the effect of nonlocal parameter at the constant values of fractional order of the heat equation and voids parameters. The nonlocal parameter is selected as ε=0, 0.2, 0.3 which also gives the comparison between local and nonlocal theories of elasticity. All the reflection coefficients show decreasing behaviour for increase in nonlocal parameter. It is important to note that in local theory of elasticity (i.e., ε=0), the magnitude of all the reflection coefficients have greater values at each angle of incidence. The magnitude of the reflection coefficients decreases due to the fact that the nonlocal stresses are long-range effective and hence they produce a weak wave. Figure 4(e) represents that the reflection of shear vertical wave does not exist at
(say). Figures 4(a)-(e) are plotted to study the nature of the reflection coefficients of the reflected waves, namely, the reflected coupled- longitudinal displacement wave, coupled-thermal wave, coupled-carrier density wave, coupled wave due to voids and the independent shear vertical wave respectively. The reflection coefficients |Zj| (j=1, 2, 3, 4, 5) are discussed under the effect of nonlocal parameter at the constant values of fractional order of the heat equation and voids parameters. The nonlocal parameter is selected as ε=0, 0.2, 0.3 which also gives the comparison between local and nonlocal theories of elasticity. All the reflection coefficients show decreasing behaviour for increase in nonlocal parameter. It is important to note that in local theory of elasticity (i.e., ε=0), the magnitude of all the reflection coefficients have greater values at each angle of incidence. The magnitude of the reflection coefficients decreases due to the fact that the nonlocal stresses are long-range effective and hence they produce a weak wave. Figure 4(e) represents that the reflection of shear vertical wave does not exist at 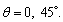
7 Conclusions
In this paper, the reflection of thermo-elastic wave in nonlocal semiconducting nanostructures medium with voids is studied. The coupled nonlocal thermo-elasticity theory of fractional order with voids is applied to studying the effects of α and ε which are fractional order time derivative and nonlocal parameter, respectively. The dispersion relation is obtained whose real roots yield four coupled-longitudinal waves and there exists an independent transverse wave in the medium. The significant results mentioned below are the main observations while taking the coupled longitudinal waves as incident wave.
1) Five waves are propagating in the semiconducting nanostructure porous medium in which four waves are coupled longitudinal wave and one wave is an independent shear vertical wave.
2) All waves are dispersive in which the coupled-longitudinal displacement wave is more dispersive, but it becomes non-dispersive for larger values of α whereas the coupled thermal wave is the least.
3) All the coupled longitudinal waves are affected by nonlocal, voids and thermal parameters but the transverse wave is only affected by nonlocal parameter.
4) The reflection coefficients |Z1| and |Z2| are decreasing with increasing values of the fractional order parameter α and the reflection coefficient of shear vertical wave has increasing effect on each angle of incidence.
5) The fractional order parameter has very weak effect on the reflection coefficient |Z3| of the coupled-carrier density wave. The reflection coefficient |Z4| of the wave due to voids first increases with α when 0°≤θ≤65°, and afterward the reverse effect is detected.
6) The reflection coefficient has greater values in local theory of elasticity for all angle of incidence as compared tonon-local theory of elasticity. Further, reflection coefficient of shear vertical wave has the maximum value at angle of incidence θ=π/4 and vanish at θ=0°, π/2.
7) The above results motivated to classify the solid materials according to their fractional order parameter α, where this parameter becomes a new indicator of its ability to conduct heat in a thermo-elastic medium.
Contributors
HASHMAT Ali provided the concept and edited the draft of manuscript. ADNAN Jahangir conducted the literature review and wrote the first draft of the manuscript. AFTAB Khan edited the draft of manuscript.
Conflict of interest
HASHMAT Ali, ADNAN Jahangir and AFTAB Khan declare that they have no conflict of interest.
References
[1] ERINGEN A C. Nonlocal continum field theories [M]. New York: Springer, 2002.
[2] ALTAN B S. Uniqueness in the linear theory of nonlocal elasticity [J]. Bulletin of the Technical University of Istanbul, 1984, 37: 373-385.
[3] CHIRITA S. On some boundary value problems in nonlocal elasticity [J]. Amale Stiinfice ale Universitatii “AL. I. CUZA” din Iasi Tomul, 1976, 22(2): 231-237.
[4] CRACIUN B. On nonlocal thermoelsticity [J]. Ann St Univ, Ovidus Constanta, 1996, 5(1): 29-36.
[5] EDELEN D G B, LAWS N. On the thermodynamics of systems with nonlocality [J]. Archive of Rational Mechanicsand Analysis,1971, 43: 24-35.
[6] EDELEN D G B, GREEN A E, LAWS N. Nonlocal continuum mechanics [J]. Archive of Rational Mechanics and Analysis, 1971, 43: 36-44.
[7] ERINGEN A C, EDELEN D G B. On nonlocal elasticity [J]. International Journal of Engineering Sciences, 1972, 10; 233-248.
[8] ERINGEN A C. Nonlocal polar elastic continua [J]. International Journal of Engineering Sciences, 1972, 10: 1-16.
[9] ERINGEN A C. Nonlocal continuum theory of liquid crystals [J]. Molecular Crystal and Liquid Crystal, 1978, 75(1): 321-343.
[10] ERINGEN A C. Memory-dependent nonlocal electromagnetic elastic solids and superconductivity [J]. Journal of Mathematical Physics, 1991, 32: 787-796.
[11] IESAN D. A theory of thermoelastic material with voids [J]. Acta Mechanica, 1986, 60: 67-89.
[12] SING D, KAUR G, TOMAR S K. Waves in nonlocal elastic solid with voids [J]. Journal of Elasticity, 2017, 128: 85-114.
[13] CASAS P S, QUINTANILLA R. Exponential decay in one-dimensional porous-themoelasticity [J]. Mechanics Research Comunications, 2005, 32: 652-658.
[14] MAGANA A, QUINTANILLA R. On the time decay of solutions in one-dimensional theories of porous materials [J]. International Journal of Solids and Structures, 2006, 43: 3414-3427.
[15] MAGANA A, QUINTANILLA R. On the time decay of solutions in porous elasticity with quasi-static micro voids [J]. Journal of Mathematical Analysis and Applications, 2007, 331: 617-630.
[16] SOUFYANE A, AFILAL M, AOUAM M, CHACHA M. General decay of solutions of a linear one-dimensional porous-thermoelasticity system with a boundary control of memory type [J]. Nonlinear Analysis, 2010, 72: 3903-3910.
[17] BACHHER M, SARKAR N, LAHIRI A. Generalized thermoelastic infinite medium with voids subjected to a instantaneous heat sources with fractional derivative heat transfer [J]. International Journal of Mechanical Science, 2014, 89: 84- 91.
[18] BACHHER M, SARKAR N, LAHIRI A. Fractional order thermoelastic interactions in an infinite porous material due to distributed time-dependent heat sources [J]. Meccanica, 2015, 50: 2167–217.
[19] BACHHER M, SARKAR N. Nonlocal theory of thermoelastic materials with voids and fractional derivative heat transfer [J]. Waves Random Complex Media, 2018, 29: 1-9.
[20] BISWAS S, SARKAR N. Fundamental solution of the steady oscillations equations in porous thermoelastic medium with dual-phase-lag model [J]. Mechanics of Materials, 2018, 126: 140-147.
[21] SARKAR N, TOMAR S K. Plane waves in nonlocal thermoelastic solid with voids [J]. Journal of Thermal Stresses, 2019, 42: 1-12.
[22] POVSTENKO Y Z. Fractional heat conduction equation and associated thermal stress [J]. Journal of Thermal Stresses, 2004, 28: 83-102.
[23] CAPUTO M. Linear models of dissipation whose Q is almost frequency independent-II [J]. Geophysical Journal International, 1967, 13: 529-539.
[24] SHERIEF H H, EL-SAYED A, EL-LATIEF A. Fractional order theory of thermoelasticity [J]. International Journal of Solid and Structures, 2010, 47: 269-275.
[25] YOUSSEF H M. Theory of fractional order generalized thermoelasticity [J]. Journal of Heat Transfer, 2010, 132: 1-7.
[26] EZZAT M A, EL-KARAMANY A S, EZZATS M. Two temperature theory in magneto-thermoelasticity with fractional order dual-phase-lag heat transfer [J]. Journal of Nuclear Eng Design, 2012, 252: 267-277.
[27] EZZAT M A, EL KARAMAN A S, MOHSEN F. Fractional order theory in thermoelastic solid with three-phase lag heat transfer [J]. Archive of Applied Mechanics, 2012, 82: 557-572.
[28] HAMZA F, ABDOU M, ABD EL-LATIEF A M. Generalized fractional thermoelasticity associated with two relaxation times [J]. Journal of Thermal Stresses, 2014, 37: 1080-1098.
[29] HAMZA F, ABDOU M, ABD EL-LATIEF A M. 1D application on fractional generalized thermoelasticity associated with two relaxation times [J]. Mechanics of Advanced Material and Structures, 2016, 23: 689-703.
[30] IBRAHIM A. Generalized thermo elastic interaction in functional graded material with Fractional order three-phase lag heat transfer [J]. Journal of Central South University, 2015, 22(5): 1606-1613.
[31] SONG Y, BAI J T, REN Z. Study on the reflection of photo-thermal waves in a semiconducting medium under generalized thermo-elastic theory [J]. Acta Mechanica, 2012, 223: 1545-1557.
[32] TANG F, SONG Y. Wave reflection in semiconductor nanostructures [J]. Theoretical and Applied mechanics Letters, 2018, 8: 160-163.
[33] IBRAHIM A, FARIS S A, AHMED E. A DPL model of photothermal interaction in a semiconductor material [J]. Waves in Random and Complex Media, 2019, 29: 328-343.
[34] JAHANGIR A, TANVIR F, ZENKOUR A M. Photo- thermo-elastic interaction in a semiconductor material with two relaxation times by a focused laser beam [J]. Advances in Aircraft and Spacecraft Sciences, 2020, 7: 41-52.
[35] ALI H, JAHANGIR A, KHAN A. Reflection of waves in arotating semiconductor nanostructure medium through torsion-free boundary condition [J]. Indian Journal of Physics, 2019. https://doi.org/10.1007/s12648-019-01652-y.
[36] SUDIPM, NIHAR S, NANTU S. Waves in dual-phase-lag thermoelastic materials with voids based on Eringen’s nonlocal elasticity [J]. Journal of Thermal Stresses, 2019, 42(8): 1035-1050.
[37] COWIN S C, NUNZIATO J W. Linear elastic materials with voids [J]. Journal of Elasticity, 1983, 13: 125-147.
[38] BACHHER M, NANTU S, LAHIRI A. Generalized thermoelastic infinite medium with voids subjected to an instantaneous heat sources with fractional derivative heat transfer [J]. International Journal of Mechanical Sciences, 2014, 89: 84-91.
[39] CHALLAMEL N, GRAZIDE C, PICANDET V, PERROT A, ZHANG Y A. A nonlocal Fourier’s law and its application to the heat conduction of one-dimensional and two- dimensional thermal lattices [J]. Comptese Rendus Mecanique, 2016, 344: 388-401.
(Edited by HE Yun-bin)
中文导读
热弹性波在半导体纳米结构非局部多孔介质中的反射
摘要:本文的工作是在含空洞的半导体纳米结构介质中将非局部弹性理论推广到分数阶热弹性理论,并对三相滞后热弹性模型中的反射现象进行了分析。研究表明,介质中存在四个耦合的纵向波和一个独立的纵向剪切波。当角频率小于截止频率时,纵波衰减,横波无衰减。膨胀波受空洞、热和非局域参数的影响,而横波只受非局部参数的影响。结果表明,反射系数受非局部参数和分数阶参数的影响。对硅材料的反射系数进行了解析计算和数值计算,并用图形进行详细讨论。作为特例,本研究得到了局部(经典)理论的结果。本研究除可应用于半导体纳米结构器件外,还可应用于地质学及地震学。
关键词:三相滞后模型;半导体;分数阶时间导数;非局部理论;纳米结构;空洞;反射
Received date: 2020-02-25; Accepted date: 2020-08-27
Corresponding author: ADNAN Jahangir, PhD, Assistant Professor; E-mail: adnan.jahangir@ciitwah.edu.pk; ORCID: https://orcid.org/ 0000-0001-5564-2754
Abstract: The current work is an extension of the nonlocal elasticity theory to fractional order thermo-elasticity in semiconducting nanostructure medium with voids. The analysis is made on the reflection phenomena in context of three-phase-lag thermo-elastic model. It is observed that, four-coupled longitudinal waves and an independent shear vertical wave exist in the medium which is dispersive in nature. It is seen that longitudinal waves are damped, and shear wave is un-damped when angular frequency is less than the cut-off frequency. The voids, thermal and non-local parameter affect the dilatational waves whereas shear wave is only depending upon non-local parameter. It is found that reflection coefficients are affected by nonlocal and fractional order parameters. Reflection coefficients are calculated analytically and computed numerically for a material, silicon and discussed graphically in details. The results for local (classical) theory are obtained as a special case. The study may be useful in semiconductor nanostructure, geology and seismology in addition to semiconductor nanostructure devices.
- Reflection of thermo-elastic wave in semiconductor nanostructures nonlocal porous medium


