参数化的空间实体变化分类方法

邢汉发¹，陈军²，李长辉¹，周晓光³

(1. 广州市城市规划勘测设计研究院，广东 广州，510060；

2. 国家基础地理信息中心，北京，100044)；

3. 中南大学 地球科学与信息物理学院，湖南 长沙，410083)

摘 要：

标标识动态性、拓扑关系、维数、形状、位置、方位等多参数的空间实体变化分类模型，为单一空间实体变化的分类描述提供了形式化方法。在此基础上，提出一种变化分类的层次推断框架，分别对单一实体9种基本变化进行细分与形式化描述，给出有意义的变化类型。最后，以变化信息标报为例，阐述其应用方式。本文所提出的层次分类方法解决了变化信息标报中“标报什么”的问题。

关键词：

更新标报；变化参数；层次分类；变化类型；

中图分类号：TD853.391          文献标志码：A         文章编号：1672-7207(2014)02-0495-06

Parametric approach to classification of spatial object change

XING Hanfa¹, CHEN Jun², LI Changhui¹, ZHOU Xiaoguang³

(1. Guangzhou Urban Planning & Design Survey Research Institute, Guangzhou 510060, China;

2. National Geomatics Center of China, Beijing 100830, China;

3. School of Geosciences and Info-physics, Central South University, Changsha 410083, China)

Abstract: A formal description model was proposed based on multi-parameter, including, identity, dynamic, dimension, shape and topological relationship in the between before and after changes. On this basis, the hierarchical inference framework of a classification of change was proposed, and each of the 9 basic changes in single entity was subdivided and formal description was given. Finally, the geo-spatial data reporting was used as an example to illustrate its application mode. The hierarchical classification method in this paper solves the questions of “what be reported” in change information reporting.

Key words: updating report; change parameters; hierarchical classification; change type

变化信息的分类与描述是时空认知科学领域的一项重要内容，其目的是认识地理空间实体变化情况，它是变化信息标报、采编、更新与服务等系统设计与开发的前提与基础，掌握基础地理空间要素的各种可能变化情况，可以提高此类系统设计的针对性，减少盲目性，还可以为系统用户提供变化信息判断依据^[1]。从面向对象的角度来看，单一实体变化分类是空间实体变化分类的基础，多个实体间的变化可以通过存在依赖关系的单个实体变化表达^[2]。Claramunt等^[2-3]将时空变化分为出现、消失、稳定、扩大、缩小、变形、移动和旋转等8大类。Egenhofer等^[4]探讨了拓朴关系的渐变规律，给出了反映拓朴关系时空变化的最邻近拓朴关系邻接图；Hornsby等^[5]从信息空间中对象状态变化的角度，将单一空间对象在时空数据库中的状态分为存在、有历史的不存在和无历史的不存在3种状态，通过这3种状态之间的组合，得出9种对象标识状态变化类型。Klippel等^[6]以“移动(move)”事件为例进行了一些人工试验，探讨了地理事件概念化的主要因素，他们认为除拓扑关系外，其他因素如对象标识(identity)、动态性 (dynamics) 等都对移动事件的概念化描述有着重要影响。Zhao等从空间一致性应用角度，以面状目标“扩大”为例，深入分析了空间对象的4个属性：形状、大小、方位角和位置的变化影响以及内在联系^[7]。他们的研究成果在国际上有着重要的影响，但其是从时空推理的角度出发，分类只是建立在枚举与图形描述的基础上，并且这些变化情况过于笼统，远不能指导变化信息标报、采编等系统的设计与开发。如：单一实体的“扩大”变化，细分情况需要从理论上选用合适的参数来进行分析与推导。国内多位学者在这方面也进行了比较深入的探索，如朱华吉^[8]从地形数据变化信息发布的应用背景出发，提出了一种基于图元快照差的变化信息描述方法，其对深化地理空间要素变化的认识有着重要的科学意义，但仍不能满足系统标报、更新需求。周晓光等^[9-11]从拓扑联动更新处理过程中的拓扑一致性维护的角度出发，推导出17种简单联动变化类型，仍然没有提出一套合适的描述模型，无法满足变化标报等应用需要。这是因为他们的研究成果仅停留在枚举与图形描述阶段，没有从理论上选用相应的参数来进行分析推导，不具备完备性。为此，本文作者在深入分析影响变化分类的重要参数基础上，提出一种能够描述和推断基本变化细分类型的形式化表达模型和推断方法，以满足变化标报、采编等GIS更新处理系统的应用需求。

1  空间实体变化的多参数形式化描述模型

扩大变化的组分类型举例如图1所示。从图1可以看出，如果将变化前后的目标投影到同一空间参考平面上，相关目标间的拓扑关系能够较好地反映出空间要素的变化情况，如图1(b)和(c)；Egenhofer等^[4-6]也从不同出发点进行的研究工作都证实了拓扑关系在变化描述中的重要性。另外，从国内外学者的研究成果来看，空间实体目标的标识与动态性、拓扑关系、维数和形状、大小、位置、方位等参数对实体的空间变化起到重要作用^{[5, 12]}。因此，本文将从将变化前、后的目标投影到同一参考平面后的拓扑关系入手，然后采用一定复杂程度下二维空间目标间(包括点/点、点/线、点/面、线/线、线/面、面/面)完备的拓扑关系类型为基础^[11]，结合要素的对象标识和动态性、维数和形状、几何特征变化等参数，建立变化信息的形式化描述模型，分析、推导出基础地理空间要素的完备变化类型。

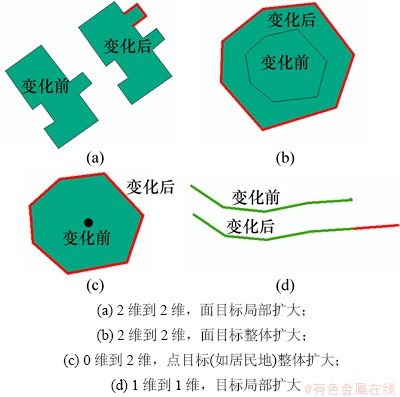
图1  扩大变化的细分类型举例

Fig. 1  Segmentation types of the expand changing

1.1  变化参数的作用及其取值

(1) 要素标识和动态性。目标标识状态是对现实世界中实体存在状态的反映，能够表达实体在现实世界中的变化情况。空间目标包括3个状态：存在、有历史的不存在和无历史的不存在。通过3种状态的变化组合可得出单一目标的9种可能变化情况^[8]，其组合后的4种变化能够对应轮廓线分类与目标标识状态变化之间的关系，即I_c={ Create, Eliminate, Continue-existence, Reincarnate }，用I_c(Value)= {02,21,22,12}，依次表示Create(新建)，Eliminate(删除)，Continue-existence(继续存在)，Reincarnate(唤醒)。目标标识对应目标的唯一Id，I_c=(Value,O_id)。例如Id为“GB101”的面目标进行“删除目标点”标报，I_c取值为(21,GB101)。

(2) 拓扑关系。一般认为，两目标间拓扑关系主要包括相离(disjoint),相邻(touch),包含(contains)、被包含(inside)，相等(equal)，部分重叠(overlap)^[13]，文中对其取值：T_p={1,2,3,4,5,6,7,8,9}。

(3) 目标维数变化。如果在变化中没有新实体出现、旧实体消失，实体维数是一个重要的参数，维数的变化在后期更新中会引起替换操作。比如居民地的扩张，由点变为面，则更新中需要将点状要素替换为面状要素，即删除点状要素，创建面状要素。文中对目标的维数变化用实际维数直接表达，即D={0,1,2}={点，线，面}。例如，维数变化D_c取值为02，表示由点变成面。

(4) 目标几何特征变化。用点状、面状和线状要素表达的客观世界的实体都是具有一定大小、方位、位置和形状等几何特征，判断描述这些地理实体的几何特征的变化可以用来确定实体的变化类型^[10]。根据线状要素和面状要素的3个基本特征：位置、形状、方位角判断2个实体是否相同，用S表示实体的形状，A表示实体的方位角，P表示实体的位置。方位角和位置参数可以用点位置和变化量组合表达，A=(R_point,M_X,M_Y)，P=(R_point,R_Degree)。空间目标的形状也是实体变化的一个重要参数，例如在数据更新中，需要将直线变为曲线，相应的变化标报和编辑过程中存在更新操作，需要删除直线要素，创建曲线要素。形状变化可用形状描述参数来表达，如线目标形状可用线的类型(如直线、圆弧、样条曲线等)来表达。目标形状取值如下：

 (1)

1.2  空间实体变化分类的形式化描述模型

本文用C_SG表示实体变化分类，I_c表示目标的标识与动态性，T_p表示拓扑关系，D_c表示目标维数的变化，S_c，P_c和A_c分别表示目标几何特征的变化参数，则可初步形成式(2)所示的六元组模型来描述与区分单一实体的变化情况。

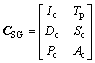              (2)

应用本文提出的变化分类模型，分别对图1中的“扩大”变化类型进行分析计算，如图2所示。它较好地描述了“扩大”变化类型的细分类型，详细分类还需基于式(2)模型进行。

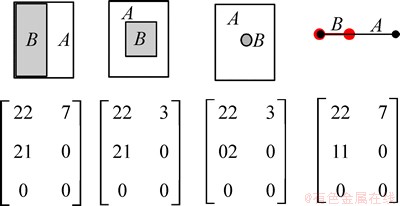
图2  基于变化分类模型的计算举例

Fig. 2  Example of calculation based on changes in classification

2  空间实体变化分类的层次细分方法

文献[11]给出了单一实体的9种基本变化类型，即出现、消失、扩大、缩小、变形、移动、旋转、重现、属性变化。但在变化信息标报、采编等系统实际应用中，仅应用基本变化分类无法满足此类系统的需求，此类系统对空间实体的变化分类信息的需求根据用户不同，是简单的、具有层次性的。例如，普通公众和专业用户对变化分类的认识和断定层次不同。因此，弄清实体的各种可能变化情况，将有助于提高此类系统设计的针对性，减少盲目性，同时还可以为系统用户提供变化信息判断依据。实体变化细分变化情况需要根据实体变化类型推断规则(或约定)来分析确定，实体变化类型推断规则需要根据式(1)模型中的变化因子来确定。

2.1  基本变化类型和细分类型的推断规则

通过对上面变化参数分析，可以得到通过空间实体“对象标识”和“几何特征变化”参数就能区分单一实体的9种基本变化类型。设A为变化后实体，B为变化前实体，则实体基本变化类型推断规则可表达为：

规则1: if (I_c=02) then Appearance(A)

即若实体A的对象标识状态从0(无历史的不存在)→2(存在)，则A为新“出现”实体。

规则2: if (I_c=21) then Disappearance (A)

即若实体A的对象标识状态从2(存在)→1(有历史的不存在)，则A为“消失”实体。

规则3: if (I_c=12) then Reappearance (A)

即若实体A的对象标识状态从1(有历史的不存在)→2(存在)，则A为“重现”实体。

规则4: if ((I_c=22) and (S_c=1)) then Expansion(B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且S(A)-S(B)>0，则变化类型为B“扩大”为A。

规则5: if ((I_c=22) and (S_c=-1)) then Contraction(B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且S(A)-S(B)<0，则变化类型为B“缩小”为A。

规则6: if ((I_c=22) and (P_c=1)) then Move(B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且A和B的位置发生变化，则变化类型为B“移动”到A。

规则7: if ((I_c=22) and (A_c=1)) then Rotation(B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且B方位角发生变化，则变化类型为B“旋转”到A。

规则(8): if ((I_c=22) and (S_c=0)and(S_c=0)and(A_c=0)) then Stability (B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且A和B的位置、大小、方位角都未发生变化，则变化类型为B发生“属性变化”。

规则9: if ((I_c=22) and (D_S=1)) then Deformation (B→A)

即若实体A的对象标识状态从2(存在)→2(存在)，且B形状发生变化，则变化类型为B“变形”为A。

2.2  实体细分变化类型的推断规则

根据式(1)模型中变化参数的取值，可从理论上推导出更为详细的单一实体的变化类型。针对9种基本变化类型的22种细分类型如图3所示。依据式(1)中变化参数的取值，剔除无意义和重复的取值，推导出有意义的空间实体详细的变化类型，并对其进行变化语义描述。

当通过I_c参数区分出“出现”、“消失”和“重现”后，则可进一步利用维数变化参数来区分“点”、“线”、“面”实体的变化类型。因此，“出现”、“消失”和“重现”的细分变化类型的推断规则如下：

规则1: if ((I_c=02)and(D_S=01)) then Appearance-Point(A); if ((I_c=02)and(D_S=11)) then Appearance-Line(A); if ((I_c=02)and(D_S=21)) then Appearance-Polygon(A);

规则2: if ((I_c=21)and(D_S=01)) then Disappearance-Point(A); if ((I_c=21)and(D_S=11)) then Disappearance-Line(A); if ((I_c=21)and(D_S=21)) then Disappearance-Polygon(A);

规则3: if ((I_c=12)and(D_S=01)) then Reappearance-Point(A); if ((I_c=12)and(D_S=11)) then Reappearance-Line(A); if ((I_c=12)and(D_S=21)) then Reappearance-Polygon(A);

即根据变化后实体A维数(01表示0维点、11表示1维简单线、21表示2维简单面)，来细分“出现”、“消失”和“重现”的变化情况。

“扩大”和“缩小”的细分变化类型可以分为2种情况：维数变化和同维数(1维线和2维面)。同维数下变化又分为“整体变化”和“局部变化”2类，它们的细分变化类型的推断规则如下：

规则4: if ((S_c=1)and(D_S=0111)) then Expansion–P2L(B→A); if ((S_c=1)and(D_S=0121)) then Expansion–P2G(B→A); if ((S_c=1)and(D_S=1121)) then Expansion–L2G(B→A);

即“扩大”细分类型中由维数变化引起的变化类型包括：“点扩大成线”(见图3中①)、“点扩大成面”(见图3中②)、“线扩大成面”(见图3中③)。

规则5: if ((S_c=1)and(T_p=7)and(D_S=11))then Expansion–Partially-Line(B→A); if ((S_c=1) and(T_p=7)and(D_S=21)) then Expansion–Partially-Polygon(B→A); if((S_c=1) and(T_p=3)and(D_S=11)) then Expansion–Wholly-Line (B→A); if((S_c=1)and(T_p=3)and(D_S=21))then Expansion–Wholly-Polygon(B→A);

即根据判断A和B拓扑关系为覆盖(cover)和包含(contains)，可以区分同维数下的“扩大”为“局部扩大”和整体扩大，规则(5)推断扩大细分类型见图3中④~⑦。

规则6: if ((S_c=-1)and(T_p=8)and(D_S=11)) then Contraction–Partially-Line(B→A); if ((S_c=-1)and(T_p=8)and(D_S=21)) then Contraction–Partially-Polygon(B→A);if((S_c=-1) and(T_p=4)and(D_S=11)) then Contraction–Wholly-Line(B→A); if((S_c=-1)and(T_p=4)and(D_S=21)) then Contraction–Wholly-Polygon(B→A);

规则7: if((S_c=-1)and(D_S=1101)) then Contraction–L2P(B→A); if ((S_c=-1)and(D_S=2101)) then Contraction–G2P(B→A); if ((S_c=-1)and(D_S=2111)) then Contraction–G2L(B→A);

规则(6)推断同维数下“缩小”细分类型见图3中8~，规则(7)推断维数“缩小”细分类型见图3中~。

 “移动”和“旋转”细分类型主要通过实体的维数来区分：

规则8: if ((P_c=1) and(D_S=01)) then Move-Point(B→A); if ((P_c=1) and(D_S=11)then Move-Line(B→A);if ((P_c=1)and(D_S=21) then Move-Polygon (B→A);

“移动”细分类型见图3中~。

规则9: if ((A_c=1)and(D_S=11)) then Rotation–Line(B→A);;if((A_c=1)and(D_S=21)) then Rotation-Polygon(B→A);

旋转细分类型见图3中和。

本文“变形”指同维数下(1维线和2维面)空间实体形状变化，依据2.2.3节中形状参数分析，变形细分变化类型跟实体形状定义类型有关，这里仅取最简单的线和面实体形状变化情况为例，来说明变形细分类型的推断规则。

图3  空间实体基本变化分类的细分类

Fig. 3  Basic changes in classification of fine classification space entity

规则10: if ((I_c=22) and (S_c=11)) then Deformation-Partially-Line(B→A); if ((I_c=22) and (S_c=21)) then Deformation-Line(B→A); if ((I_c=22) and (S_c=22)) then Deformation-Polygon(B→A);

推断“变形”细分类型见图3中~。

从规则1~9可以推断出空间实体9种基本变化分类的22种细分类型，其层次分类推断框架如图4所示，包括基本变化分类和细分变化分类2个层次，用户可以根据不同需求，对变化类型进行多层次判断。

下面简要说明空间实体层次分类的完备性。空间实体变化不仅包括实体的属性、位置、形状的变化，也包括拓扑关系的变化，这才能使得空间变化描述具备完备性^{[12, 14]}。本文提出的空间实体变化分类方法中的6个变化参数，包括了上述变化分类的完备性描述因子；其中，大小、位置和方位参数相互独立，维数和拓扑关系虽然有一定关联，本文已对其关系进行了分类处理；分类模型中的参数与空间实体基本变化类型存在对应关系，如变化参数“目标标识状态”对应“出现”、“消失”；“方位角”对应“旋转”；“位置”对应“移动”；“大小”对应“扩大”、“缩小”等，这些变化参数组合可以较为全面的描述上述基本变化类型的组合变化类型；模型分别对点、线、面进行空间实体详细变化分类，满足了GIS应用中不同地形要素类型的变化分类需求。因此，本文提出的分类方法在一定复杂程度下具备完备性。

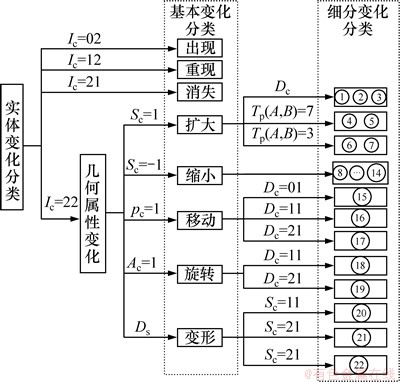
图4  空间实体变化分类的层次推断框架

Fig. 4  Hierarchical inference framework of space entity change classification

3  应用实例

空间实体变化分类是变化信息标报、采编等系统设计与开发的前提与基础。本文以地形要素变化信息标报为例，讲述作者提出的层次分类方法在GIS更新系统中的具体应用。以实际的地图服务数据(见图5)为依据，模拟各种变化类型，进行了变化分类在变化信息标报中的试验。在试验系统中，变化信息分类包括基本类型和细分类型2个层次；将用户划分为普通公众和专业用户。如图5所示，以“居民地扩大”变化标报为例，当不同用户进行变化标报时，他们理解和选择的变化类型很有可能不同。如一般普通公众地图专业背景相对欠缺，对变化信息判断可能处于基本变化类型层次，要素变化类型选择为“扩大”；专业用户需要对系统定义的变化类型判断规则进行一定的培训，能够提供较为详细的变化情况，为后续变化信息采编、变化信息服务等应用提供操作依据。它们对变化信息判断处于细分变化类型层次，变化类型选择为“面目标整体扩大”。该实例证明了层次分类方法在变化信息标报系统应用中的可行性，解决了变化信息标报中“标报什么”的问题。

图5  层次分类方法在变化信息标报中的应用

Fig. 5  Application of hierarchical classification method on change information plotting

4  结论

(1) 从变化信息标报、采编等系统的实际应用入手，以面向对象理论为基础建立单一实体变化的分类描述模型和层次分类框架，分别对空间实体基本变化类型进行分析推断，细分出有意义的变化类型，并对其进行变化语义描述。

(2) 通过实例分析，并从理论上选用相应的变化参数来进行分析推导，从而提出了一种基于目标标识动态性、拓扑关系、维数、形状、位置、方位等多参数的空间实体变化形式化描述模型和层次分类框架，较好地解决了单一实体的形式化分类与描述难题，它可以完备描述空间实体变化情况。

参考文献：

[1] 陈军, 林艳, 刘万增, 等. 面向更新的空间目标快照差分类与形式化描述[J]. 测绘学报, 2012, 1(2): 108-114.

CHEN Jun, LIN Yan, LIU Wanzeng, et al. Formal classification of spatial incremental changes for updating[J]. Acta Geodaetica et Cartographica Sinica, 2012, 1(2): 108-114.

[2] Claramunt C, Thériault M. Managing time in GIS an event-oriented approach. recent advances on temporal databases[M]. Clifford J, Tuzhilin A. Zurich: Springer-Verlag, 1995: 23-42.

[3] Couclelis H. Aristotelian spatial dynamics in the age of geographic information systems[M]. New York: Oxford University Press, 1998: 109-118.

[4] Egenhofer M J, Al-taha K K, Goos G, et al. Reasoning about gradual change of topological relationships[J]. Lecture Notes in Computer Science, 1992, 639: 196-219.

[5] Hornsby K, Egenhofer M. Identity-based change: A foundation for spatio-temporal knowledge representation[J]. International Journal of Geographical Information Science, 1992(3): 207-224.

[6] Klippel A, Worboys M, Duckham M. Identifying factors of geographic event conceptualisation[J]. International Journal of Geographical Information Science, 2008(2): 183-204.

[7] ZHAO Zuoquan, Stough R R, SONG Dunjiang. Measuring congruence of spatial objects[J]. International Journal of Geographical Information Science, 2011, 3(1): 113-130.

[8] 朱华吉. 地形数据库增量信息数据建模及其RDF描述[J]. 吉林大学学报(地球科学版), 2007, 37(1): 195-199.

ZHU Huaji. Modeling of incremental information in topographic database and its description based on RDF[J]. Journal of Jilin University(Earth Science Edition), 2007, 37(1): 195-199.

[9] 周晓光, 陈军, 李志林. 基于欧拉数的地籍拓扑关系计算与应用[J]. 测绘学报, 2006, 35(3): 291-298.

ZHOU Xiaoguang, CHEN Jun, LI Zhilin. Computation of topological relations between cadastral objects based on euler-number[J]. Acta Geodaetica et Cartographica Sinica, 2006, 35(3): 291-298.

[10] ZHOU Xiaoguang, CHEN Jun, JIANG Jie, et al. Event-based incremental updating of spatio-temporal database[J]. Journal of Central South University of Technology, 2004, 11(2): 192-198.

[11] 陈军, 周晓光. 基于拓扑联动的增量更新方法研究[J]. 测绘学报, 2008, 37(3): 322-329.

CHEN Jun, ZHOU Xiaoguang. Incremental updating of spatial database based on topological linkage, taking cadastral database’s updating as an example[J]. Acta Geodaetica et Cartographica Sinica, 2008, 37(3): 322-329.

[12] Raza A, Kainz W. An object-oriented approach for modeling urban land-use changes[J]. URISA Journal, 2002, 14(1): 37-55.

[13] 郑扣根, 谭石禹, 潘云鹤. 基于状态和变化的统一时空数据模型[J]. 软件学报, 2001, 12(9): 1360-1365.

ZHENG Kougen, TAN Shiyu, PAN Yunhe. A unified spatio-temporal data model based on state and change[J]. Journal of Software, 2001, 12(9): 1360-1365.

[14] Clementini E, Felice P Di. A comparison of methods for representing topological relationships[J]. Information Sciences, 1995, 2(3): 149-178.

(编辑  赵俊)

收稿日期：2013-06-25；修回日期：2013-09-20

基金项目：国家自然科学基金面上资助项目(41371366)；广州市科技计划项目(2012Y2-00035；2013Y2-00031)

通信作者：邢汉发(1981-)，男，山东淄博人，博士，从事地理信息空间数据建模、更新、服务等方面的研究；电话：18588861619；E-mail：xinghanfa@163.com

摘要：提出一种基于目标标识动态性、拓扑关系、维数、形状、位置、方位等多参数的空间实体变化分类模型，为单一空间实体变化的分类描述提供了形式化方法。在此基础上，提出一种变化分类的层次推断框架，分别对单一实体9种基本变化进行细分与形式化描述，给出有意义的变化类型。最后，以变化信息标报为例，阐述其应用方式。本文所提出的层次分类方法解决了变化信息标报中“标报什么”的问题。