横观各向同性岩石弹性参数及抗压强度的试验研究
刘运思,傅鹤林,伍毅敏,饶军应,尹泉,袁维
(中南大学 土木工程学院,湖南 长沙,410075)
摘 要:
石力学特性的各向异性,对7种不同层理角度q下的板岩进行单轴压缩试验,测出了板岩的弹性模量E和E′、泊松比ν和ν′以及剪切模量G′,并运用单弱面理论分析单轴抗压强度和破坏形式与层理角度之间的关系。研究结果表明板岩压缩破坏存在2种形式:当0°≤q<10.5°和87.0°<q≤90.0°时,板岩从内部发生压缩剪切破坏,剪切面粗糙不平;当10.5°≤q≤87.0°时,板岩沿层理面产生滑移破坏,表面较光滑。板岩受内部层理构造的影响,随着q从0°变化到90°,抗压强度呈现两端大中间小的趋势,视弹性模量Eθ以及视泊松比νyx和νyz由小变大。
关键词:
中图分类号:TU 458 文献标志码:A 文章编号:1672-7207(2013)08-3398-07
Experimental study of elastic parameters and compressive strength for transversely isotropic rocks
LIU Yunsi, FU Helin, WU Yimin, RAO Junying, YIN Quan, YUAN Wei
(School of Civil Engineering, Central South University, Changsha 410075, China)
Abstract: To reveal the anisotropy of mechanical properties for layered rock, the five elastic parameters on uniaxial tests under seven different kinds of bedding angle q were measured, and the relationship among the uniaxial compressive strength and failure mode and the bedding angle q were explained by single discontinuity theory. The results show that there are internal compression shear failure and shear surface failure. Both of the failure forms take place while the bedding angle is 0°≤q<10.5° and 87.0°<q≤90.0°. When the bedding angle is 10.5°≤q≤87.0° sliding failure of the bedding plane happens and the failure surface becomes very smooth. Because of the impact of internal bedding structure on the slate, the compressive strength reaches its minimum value in the middle and maximum value on two sides with the bedding angle θ varies from 0° to 90.0°. Moreover, the apparent elastic modulus Eθ and Poisson's ratio of νyx and νyz increase from small to large.
Key words: rock mechanics; transversely isotropic; elastic parameter; compressive strength; failure modes
在一般情况下,人们将变形的层理状岩石作为横观各向同性体来研究其力学行为[1-2]。目前,针对各向异性岩石力学性质的研究主要集中在以下几个方面:(1) 弹性变形参数测定方法[3];(2) 各向异性强度和屈服准则[4-7];(3) 各向异性岩石弹塑性本构模型[8-10]。这些研究对深入认识各向异性岩石弹塑性力学性质具有重要意义。关于横观各向同性岩石弹性变形参数测定方法,为了减少测试大量岩样的繁琐工作,Saint-Venant提出了经验公式,认为剪切模量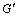 与E,
与E, 和
和 存在函数关系,将横观各向同性岩石5个弹性参数减少至4个。Worotnicki[11]通过试验发现,仅仅在低各向异性度时,横观各向异性岩石满足Saint-Venant经验公式。此后,Talesnick等[12]仅用1个薄壁空心圆柱岩样测出5个弹性参数,但需同时对岩样进行轴向压缩、环向压缩和扭转,这对试验设备要求较高,不利于开展常规试验。Gonzaga等[13]使用单轴压缩仪和三轴压缩仪组成一个液压静力压缩系统,对1个薄壁空心圆柱试样进行试验,测出了5个弹性参数。但这种方法仍然依赖于Saint-Venant经验公式,当试样轴线平行于各向同性面时,考虑没有剪切应变存在。此外,国内外对横观各向同性岩石强度的各向异性研究较多,从最初的单轴和三轴压缩试验都证实了层状岩石的抗压强度随层理角度的变化而变化。刘卡丁等[14]分析了应力状态、层面方位等对剪切破坏面方向的影响。余天堂等[15-16]通过引入1个二阶损伤张量来反映岩体几何特征的影响,建立了节理岩体各向异性屈服准则。以往的这些研究常常是理论分析多于试验研究,且没有形成一套完整的有关层状、似层状结构岩体力学性质参数的试验成果及成熟的取值原则。Hoek等[17-18]建立的Hoek-Brown经验强度准则通过引入经验常数m与s,也较好地解释了结构面的影响,并在一些工程中得到了较好的应用,但这一准则中的m与s很难确定,因此,用来预测岩体强度有困难。为此,本文作者针对横观各向同性岩石测试5个弹性参数、强度和破坏准则等尚未解决的问题,首先讨论横观各向同性岩石的5个弹性变形参数测试方法,并以板岩的单轴加卸载应力-应变曲线为基础,测出5个弹性参数;然后,基于单弱面理论,分析板岩的抗压强度随结构面的变化情况;最后,通过单轴压缩破坏试验,揭示板岩破坏形式分为顺层理面滑移破坏和剪切破坏2种形式,以便为类似处于抗压状态的层状岩体结构工程分析提供参考。
存在函数关系,将横观各向同性岩石5个弹性参数减少至4个。Worotnicki[11]通过试验发现,仅仅在低各向异性度时,横观各向异性岩石满足Saint-Venant经验公式。此后,Talesnick等[12]仅用1个薄壁空心圆柱岩样测出5个弹性参数,但需同时对岩样进行轴向压缩、环向压缩和扭转,这对试验设备要求较高,不利于开展常规试验。Gonzaga等[13]使用单轴压缩仪和三轴压缩仪组成一个液压静力压缩系统,对1个薄壁空心圆柱试样进行试验,测出了5个弹性参数。但这种方法仍然依赖于Saint-Venant经验公式,当试样轴线平行于各向同性面时,考虑没有剪切应变存在。此外,国内外对横观各向同性岩石强度的各向异性研究较多,从最初的单轴和三轴压缩试验都证实了层状岩石的抗压强度随层理角度的变化而变化。刘卡丁等[14]分析了应力状态、层面方位等对剪切破坏面方向的影响。余天堂等[15-16]通过引入1个二阶损伤张量来反映岩体几何特征的影响,建立了节理岩体各向异性屈服准则。以往的这些研究常常是理论分析多于试验研究,且没有形成一套完整的有关层状、似层状结构岩体力学性质参数的试验成果及成熟的取值原则。Hoek等[17-18]建立的Hoek-Brown经验强度准则通过引入经验常数m与s,也较好地解释了结构面的影响,并在一些工程中得到了较好的应用,但这一准则中的m与s很难确定,因此,用来预测岩体强度有困难。为此,本文作者针对横观各向同性岩石测试5个弹性参数、强度和破坏准则等尚未解决的问题,首先讨论横观各向同性岩石的5个弹性变形参数测试方法,并以板岩的单轴加卸载应力-应变曲线为基础,测出5个弹性参数;然后,基于单弱面理论,分析板岩的抗压强度随结构面的变化情况;最后,通过单轴压缩破坏试验,揭示板岩破坏形式分为顺层理面滑移破坏和剪切破坏2种形式,以便为类似处于抗压状态的层状岩体结构工程分析提供参考。
1 横观各向同性弹性变形参数
1.1 岩石横观各向同性
横观各向同性体受力模型如图1所示。图1中:x,y和z为基本坐标系; ,
,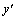 和
和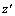 为与横观各向同性面保持一致的坐标系;x与
为与横观各向同性面保持一致的坐标系;x与 的夹角为
的夹角为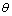 。
。
根据胡克定理[19],可知横观各向同性材料应力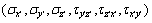 与应变
与应变

 的关系式:
的关系式:

图1 横观各向同性受力模型
Fig.1 Model of diagram transversely isotropic
 (1)
(1)
式中:E和 分别为平行于横观各向同性面的弹性模量和泊松比;
分别为平行于横观各向同性面的弹性模量和泊松比; ,
, 和
和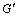 分别为垂直于横观各向同性面的弹性模量、泊松比和剪切模量。
分别为垂直于横观各向同性面的弹性模量、泊松比和剪切模量。
Amadei[3]认为含层理面的岩石应力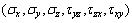 与应变
与应变 的关系不仅与5个弹性参数
的关系不仅与5个弹性参数 有关,还与层理角度
有关,还与层理角度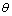 有关:
有关:
 (2)
(2)
轴向应力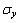 与应变
与应变 存在如下关系:
存在如下关系:
 (3)
(3)
式中:a12,a22,a32和a26是由θ和5个弹性参数 决定的函数关系式,其表达式为
决定的函数关系式,其表达式为
 (4)
(4)
1.2 岩石横观各向同性弹性参数测试方法
分别对θ=0°和90°以及θ≠0°且θ≠90°时进行单轴压缩试验,可测出横观各向同性岩石5个弹性参数,如图2所示。
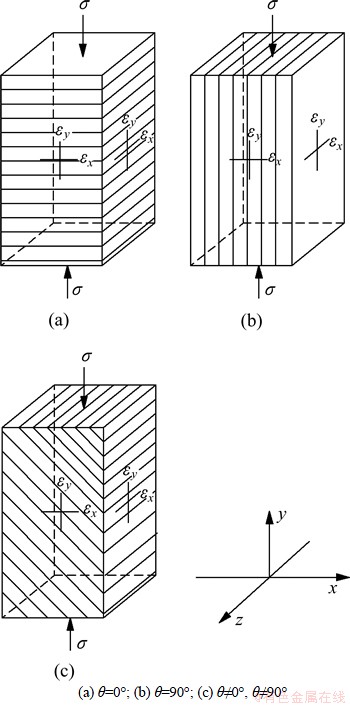
图2 单轴试验弹性参数测试方法
Fig.2 Uniaxial testing method of elastic parameters
(a) 当θ=0°时(如图2(a)所示),由式(3)和(4)得:
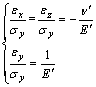 (5)
(5)
(b) 当θ=90°时(如图2(b)所示),由式(3)和(4)得:
 (6)
(6)
(c) 当θ≠0°或90°时(如图2(c)所示),由式(4)和(3)得:
 (7)
(7)
由式(5)~(7)可知应变和应力的比值 与5个未知的弹性参数
与5个未知的弹性参数 存在如下线性关系:
存在如下线性关系:
 (8)
(8)
式中: 为N×1阶矩阵;[T]为含θ的N×5阶矩阵;[C]为5个未知的弹性参数
为N×1阶矩阵;[T]为含θ的N×5阶矩阵;[C]为5个未知的弹性参数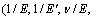
 。
。
2 单轴试验
2.1 试验材料
试验所用板岩均是在怀通(怀化—通道)高速公路第24标段正团冲隧道内采集。岩样采集后,采用直径为50 mm的钻头沿不同层理角度进行钻孔。经过切割和打磨成标准试样(长径比为2:1),岩石试样表面光滑,上、下表面的平行度控制在0.5 mm,表面的平面度控制在0.1 mm。共取样37个,试验成功28个。
2.2 试验方法及设备
本次单轴试验方案是对θ=0°和90°时(见图3(a)和(b))以及θ≠0°且θ≠90°时(见图3(c))的试样进行加载。为了研究不同层理角度对单轴试验的影响,本次试验取θ分别为0°,15°,30°,45°,60°,75°和90°进行试验,共4组。单轴实验示意图见图3。
试样四侧贴有应变片,对水平和竖向应变进行量测。试验在YE-2000型压力试验机上进行,最大试验力为2 MN,精度等级为1级,加载速率控制为0.1 kN/s,如图4所示。

图3 q =0°~90°时单轴试验示意图
Fig.3 Sketches of uniaxal test when q =0°~90°)
3 弹性模量与层理角度的关系
3.1 横观各向同性的5个弹性参数
Saint-Venant认为横观各向同性岩石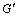 与E,
与E, ,
, 和
和 存在函数关系[11]。此时,
存在函数关系[11]。此时,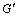 用
用 代替,其表达式为:
代替,其表达式为:
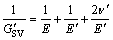 (9)
(9)
式中: 为Saint-Venant经验公式的剪切模量。
为Saint-Venant经验公式的剪切模量。
根据单轴试验测得28个试样应力与应变,代入式(8)和(9),计算得到弹性参数,见表1; 与
与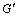 的关系见图4。
的关系见图4。
由表1可知:平均弹性模量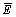 和
和 分别为35.33 GPa和24.70 GPa,平均剪切模量
分别为35.33 GPa和24.70 GPa,平均剪切模量 为12.09 GPa,平均泊松比
为12.09 GPa,平均泊松比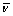 和
和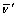 分别为0.286和0.219。
分别为0.286和0.219。 的平均值为1.43,
的平均值为1.43,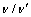 的平均值为1.31,板岩显示出低各向异性。
的平均值为1.31,板岩显示出低各向异性。
Worotnicki[11]认为岩石在低各向异性度时, 与E,
与E, ,
, 和
和 存在式(9)的函数关系。由表1和图4可知:4组试样所得
存在式(9)的函数关系。由表1和图4可知:4组试样所得 与
与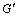 的相对误差分别12%,29%,9%和21%,平均相对误差为18%。因此,岩体在低各向异性度时不满足Saint-Venant经验公式。由研究结论可知:
的相对误差分别12%,29%,9%和21%,平均相对误差为18%。因此,岩体在低各向异性度时不满足Saint-Venant经验公式。由研究结论可知: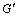 ,E,
,E, ,
, 和
和 是相互独立的5个弹性参数,不存在函数关系。这与Cho等[19]研究得到的结论一致。
是相互独立的5个弹性参数,不存在函数关系。这与Cho等[19]研究得到的结论一致。

图4  与
与 的关系
的关系
Fig.4 Relationship between  and
and 
3.2 视弹性模量和视泊松比
根据式(3)和(4),视弹性模量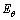 和视泊松比
和视泊松比 和
和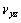 与5个弹性参数存在函数关系:
与5个弹性参数存在函数关系:
 ;
; ;
;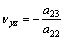 (10)
(10)
根据式(10)可求出视弹性模量理论值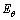 (图5(b))以及视泊松比理论值
(图5(b))以及视泊松比理论值 和
和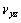 (见图6)。
(见图6)。
从图5(a)和图6可见:板岩随着层理角度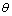 从0°变化到90°,视弹性模量由小变大,泊松比
从0°变化到90°,视弹性模量由小变大,泊松比 和
和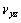 由小变大。其原因是试件内部由薄片状结构间的间隙来抵抗压应力逐渐转变为薄片状结构,而薄片状结构间的间隙抵抗压应力较低。由图5(b)和图6可见:平均视弹性模量
由小变大。其原因是试件内部由薄片状结构间的间隙来抵抗压应力逐渐转变为薄片状结构,而薄片状结构间的间隙抵抗压应力较低。由图5(b)和图6可见:平均视弹性模量 和视泊松比
和视泊松比 和
和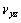 接近于理论计算值,证明此种方法能较准确地测得弹性参数。
接近于理论计算值,证明此种方法能较准确地测得弹性参数。
表1 弹性参数计算结果
Table 1 Calculation results of elastic parameters
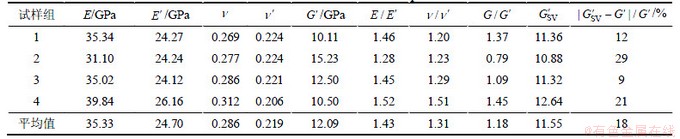

图5 视弹性模量试验值与理论值
Fig.5 Experimental and theoretical values of apparent elastic modulus

图6 视泊松比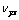 和
和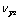 试验值和理论值
试验值和理论值
Fig.6 Experimental and theoretical values of apparent Poission’s ratio 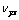 and
and 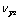
4 强度和破坏形式与层理角度的关系
4.1 单弱面理论
Jeager[20]建立的单结构面理论如下:岩体中发育有一组结构面,假定结构面与最大主平面的夹角为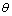 ,由莫尔应力圆理论(见图7)可知,结构面上法向正应力和剪切应力的表达式为
,由莫尔应力圆理论(见图7)可知,结构面上法向正应力和剪切应力的表达式为
 (11)
(11)
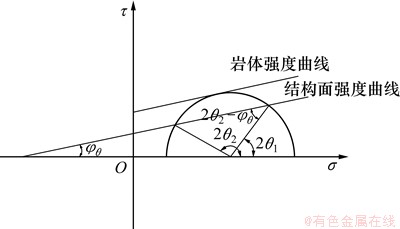
图7 单结构面理论示意图
Fig.7 Model of single inclined discontinuity theory
假定结构面的抗剪强度 服从莫尔-库仑准则,则有
服从莫尔-库仑准则,则有
 (12)
(12)
式中: 为结构面上内摩擦角;
为结构面上内摩擦角; 为结构面上内凝聚力。在单轴压缩试验下,
为结构面上内凝聚力。在单轴压缩试验下,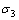 为0 MPa,将式(11)代入式(12)得:
为0 MPa,将式(11)代入式(12)得:
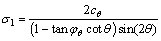 (13)
(13)
利用图7中的三角关系可知:
 (14)
(14)
当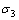 为0时,简化整理后可求得:
为0时,简化整理后可求得:
 (15)
(15)
同理,可求得:
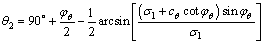 (16)
(16)
4.2 层理角度对单轴抗压强度的影响
岩石单轴抗压强度可以表示为
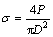 (17)
(17)
式中: 为岩石抗压强度;D为直径;P为试样破坏荷载。抗压强度计算结果见表2。
为岩石抗压强度;D为直径;P为试样破坏荷载。抗压强度计算结果见表2。
表2 抗压强度计算结果
Table 2 Calculations of compressive strength MPa

通过最小二乘法将表2中数值代入式(13)进行拟合,可以得到岩体中结构面上的 和
和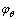 分别为7.57 MPa和7.51°,考虑层理面单轴抗压强度公式为
分别为7.57 MPa和7.51°,考虑层理面单轴抗压强度公式为
 (18)
(18)
图8所示为拟合得到的考虑层理面单轴抗压强度包络线和4组试验的平均值。由图8可知:随着层理角度θ从0°变化到90°,抗压强度呈现中间小两头大的趋势;拟合得到结果和试验结果接近,该公式能较好地反映了抗压强度随层理角度变化规律。

图8 抗压强度的试验结果和理论结果
Fig.8 Experimental and theoretical results of compressive strength
4.3 层理角度对破坏形式的影响
由式(13)可知,当θ→90°,θ→0°或θ→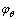 时,
时, →∞,岩体不可能沿结构面破坏,而是穿切结构面。在层状岩石材料中,只有当θ1≤θ≤θ2时,岩体才沿结构面破坏。根据式(15)和式(16)计算得到θ1和θ2分别为10.5°和87.0°,因此,单轴压缩破坏形式主要分为2种:顺层理面滑移破坏和剪切破坏。当0°≤θ<10.5°和87.0°<θ≤90.0°时,板岩可以从内部发生压缩剪切破坏,剪切面粗糙不平;当10.5°≤θ≤87.0°时,板岩会沿层理面产生滑动破坏,表面较光滑。图10所示为试样2种破坏形式。
→∞,岩体不可能沿结构面破坏,而是穿切结构面。在层状岩石材料中,只有当θ1≤θ≤θ2时,岩体才沿结构面破坏。根据式(15)和式(16)计算得到θ1和θ2分别为10.5°和87.0°,因此,单轴压缩破坏形式主要分为2种:顺层理面滑移破坏和剪切破坏。当0°≤θ<10.5°和87.0°<θ≤90.0°时,板岩可以从内部发生压缩剪切破坏,剪切面粗糙不平;当10.5°≤θ≤87.0°时,板岩会沿层理面产生滑动破坏,表面较光滑。图10所示为试样2种破坏形式。

图9 部分试样破坏照片
Fig.9 Photos of part of sample failures
5 结论
(1) 通过单轴试验测出了板岩5个弹性参数,其中 的平均值为1.43,
的平均值为1.43,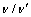 的平均值为1.31,板岩显示出明显的各向异性。
的平均值为1.31,板岩显示出明显的各向异性。
(2) 板岩随着层理角度θ从0°变化到90°,视弹性模量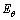 和泊松比
和泊松比 和
和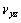 由小变大。
由小变大。
(3) 根据单弱面理论,拟合得到结构面上 和
和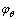 较低,很好地反映了沿结构面滑移破坏的抗压强度远低于沿内部结构剪切破坏的抗压强度;建立的抗压强度和层理角度关系式与试验结果较吻合,验证了随着层理角度θ从0°变化到90°,抗压强度呈两端大中间小的趋势。
较低,很好地反映了沿结构面滑移破坏的抗压强度远低于沿内部结构剪切破坏的抗压强度;建立的抗压强度和层理角度关系式与试验结果较吻合,验证了随着层理角度θ从0°变化到90°,抗压强度呈两端大中间小的趋势。
(4) 板岩层理角度不同,其单轴压缩破坏形式主要分为2种:顺层理面滑移破坏和剪切破坏。当0°≤ θ<10.5°和87.0°<θ≤90.0°时,板岩可以从内部发生压缩剪切破坏,剪切面粗糙不平;当10.5°≤θ≤87.0°时,板岩会沿层理面产生滑动破坏,表面光滑。
参考文献:
[1] Hakala M, Kuula H, Hudson J A. Estimating the transversely isotropic elastic intact rock properties for in situ stress measurement data reduction: A case study of the Olkiluoto mica gneiss, Finland[J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(1): 14-46.
[2] 刘运思, 傅鹤林.不同层理方位影响下板岩各向异性巴西圆盘劈裂试验研究[J]. 岩石力学与工程学报, 2012, 31(4): 785-791.
LIU Yunsi, FU Helin. Research on Brazilian disc splitting tests for anisotropy of slate under influence of different bedding orientations[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(4): 785-791.
[3] Amadei B. Importance of anisotropy when estimating and measuring in situ stresses in rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1996, 33(3): 293-325.
[4] Duveau D, Shao J F, Henry J P. Assessment of some failure criteria for strongly anisotropic geomaterials[J]. Mechanics of Cohesive-frictional Materials, 1998, 3(1): 1-26.
[5] Cazacu O, Cristescu N D. A paraboloid failure surface for transversely isotropic materials[J]. Mechanics of Materials, 1999, 31(6): 381-393.
[6] Tien Y M, Kuo M C. A failure criterion for transversely isotropic rocks[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(3): 399-412.
[7] Pietruszczak S, Mroz Z. Formulation of anisotropic failure criteria incorporating a microstructure tensor[J]. Computers and Geotechnics, 2000, 26(2): 105-112.
[8] Pietruszczak S. On inelastic behaviour of anisotropic frictional materials[J]. Mechanics of Cohesive-frictional Materials, 1999, 4(3): 281-293.
[9] Pietruszczak S, Lydzba D, Shao J F. Modelling of inherent anisotropy in sedimentary rocks[J]. International Journal of Solids and Structures, 2002, 39(3): 637-648.
[10] Lade P V. Modeling failure in cross-anisotropic frictional materials[J]. International Journal of Solids and Structures, 2007, 44(16): 5146-5162.
[11] Worotnicki G. CSIRO triaxial stress measurement cell[C]//Hudson J A. Comprehensive rock engineering. Oxford: Pergamon Press, 1993: 329-334.
[12] Talesnick M L, Ringel M. Completing the hollow cylinder methodology for testing of transversely isotropic rocks: torsion testing[J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(5): 627-639.
[13] Gonzaga G G, Leite M H, Corthesy R. Determination of anisotropic deformability parameters from a single standard rock specimen[J]. International Journal of Rock Mechanics and Mining Sciences, 2008, 45(8): 1420-38.
[14] 刘卡丁, 张玉军. 层状岩体剪切破坏面方向的影响因素[J]. 岩石力学与工程学报, 2002, 21(3): 335-339.
LIU Kading, ZHANG Yujun. Influence factors on shear failure orientation of layered rocks[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(3): 335-339.
[15] 余天堂. 岩土材料固有各向异性的模拟[J]. 岩石力学与工程学报, 2004, 23(10): 1604-1607.
YU Tiantang. Modeling of inherent anisotropy for geotechnical material[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(10): 1604-1607.
[16] 杨强, 陈新, 周维垣. 基于二阶损伤张量的节理岩体各向异性屈服准则[J]. 岩石力学与工程学报, 2005, 24(8): 1275-1282.
YANG Qiang, CHEN Xin, ZHOU Weiyuan. Anisotropic yield criterion for jointed rock masses based on a two-order damage tensor[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(8): 1275-1282.
[17] Hoek E. Strength of jointed rock masses[J]. Geotechnique, 1983, 33(3): 187-223.
[18] Saroglou H, Tsiambaos G. A modified Hoek–Brown failure criterion for anisotropic intact rock[J].International Journal of Rock Mechanics and Mining Sciences, 2008, 45(2):223-234.
[19] Cho J W, Kim H. Deformation and strength anisotropy of Asan gneiss, Boryeong shale, and Yeoncheon schist[J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 50(2): 158-169.
[20] Jaeger J C. Shear failure of anisotropic rock[J]. Geological Magazine, 1960, 97: 65-72.
(编辑 陈灿华)
收稿日期:2012-10-08;修回日期:2013-01-20
基金项目:国家自然科学基金资助项目(51008308,51108397);湖南省研究生创新项目(CX2012B057)
通信作者:刘运思(1985-),男,湖南长沙人,博士研究生,从事岩石力学、边坡等研究;电话:18573103818;E-mail: liuyunsi@sohu.com
摘要:为了揭示层状岩石力学特性的各向异性,对7种不同层理角度q下的板岩进行单轴压缩试验,测出了板岩的弹性模量E和E′、泊松比ν和ν′以及剪切模量G′,并运用单弱面理论分析单轴抗压强度和破坏形式与层理角度之间的关系。研究结果表明板岩压缩破坏存在2种形式:当0°≤q<10.5°和87.0°<q≤90.0°时,板岩从内部发生压缩剪切破坏,剪切面粗糙不平;当10.5°≤q≤87.0°时,板岩沿层理面产生滑移破坏,表面较光滑。板岩受内部层理构造的影响,随着q从0°变化到90°,抗压强度呈现两端大中间小的趋势,视弹性模量Eθ以及视泊松比νyx和νyz由小变大。
[2] 刘运思, 傅鹤林.不同层理方位影响下板岩各向异性巴西圆盘劈裂试验研究[J]. 岩石力学与工程学报, 2012, 31(4): 785-791.
[14] 刘卡丁, 张玉军. 层状岩体剪切破坏面方向的影响因素[J]. 岩石力学与工程学报, 2002, 21(3): 335-339.
[15] 余天堂. 岩土材料固有各向异性的模拟[J]. 岩石力学与工程学报, 2004, 23(10): 1604-1607.
[16] 杨强, 陈新, 周维垣. 基于二阶损伤张量的节理岩体各向异性屈服准则[J]. 岩石力学与工程学报, 2005, 24(8): 1275-1282.
[17] Hoek E. Strength of jointed rock masses[J]. Geotechnique, 1983, 33(3): 187-223.
[20] Jaeger J C. Shear failure of anisotropic rock[J]. Geological Magazine, 1960, 97: 65-72.


