J. Cent. South Univ. (2017) 24: 1602-1611

DOI: 10.1007/s11771-017-3565-y

TANG Gao-peng(唐高朋), ZHAO Lian-heng(赵炼恒), LI Liang(李亮), CHEN Jing-yu(陈静瑜)

School of Civil Engineering, Central South University, Changsha 410075, China

Central South University Press and Springer-Verlag Berlin Heidelberg 2017

Abstract:

The combined influence of nonlinearity and dilation on slope stability was evaluated using the upper-bound limit analysis theorem. The mechanism of slope collapse was analyzed by dividing it into arbitrary discrete soil blocks with the nonlinear Mohr–Coulomb failure criterion and nonassociated flow rule. The multipoint tangent (multi-tangent) technique was used to analyze the slope stability by linearizing the nonlinear failure criterion. A general expression for the slope safety factor was derived based on the virtual work principle and the strength reduction technique, and the global slope safety factor can be obtained by the optimization method of nonlinear sequential quadratic programming. The results show better agreement with previous research result when the nonlinear failure criterion reduces to a linear failure criterion or the non-associated flow rule reduces to an associated flow rule, which demonstrates the rationality of the presented method. Slope safety factors calculated by the multi-tangent inclined-slices technique were smaller than those obtained by the traditional single-tangent inclined-slices technique. The results show that the multi-tangent inclined-slices technique is a safe and effective method of slope stability limit analysis. The combined effect of nonlinearity and dilation on slope stability was analyzed, and the parameter analysis indicates that nonlinearity and dilation have significant influence on the result of slope stability analysis.

Key words:

slope stability analysis; nonlinear failure criterion; non-associated flow rule; multipoint tangent technique; upper-bound limit analysis theorem；

1 Introduction

Extensive research has confirmed that geotechnical materials have significantly nonlinear mechanical properties and the failure envelopes of geotechnical materials are curved, especially in the range of low normal effective stresses [1-4]. In engineering practice, the dilation angle of a geotechnical material is not identical to its friction angle, and geotechnical materials are subjected to non-associated flow rules [5-7]. Many studies have been conducted on slope stability analysis with the geotechnical material characteristics mentioned above taken into consideration. Most such studies, however, have only considered the influence of a nonlinear failure criterion or a non-associated flow rule on slope stability on the basis of limit analysis theory.

For the convenience in employing a nonlinear form of the Mohr–Coulomb (M–C) failure criterion in analyzing slope stability, ZHANG and CHEN [8] adopted an “inverse method” to obtain a stability factor (N_s) for homogenous slopes using a nonlinear M–C failure criterion. The external tangent technique proposed by COLLINS et al [9], which is more convenient than the inverse method, has been used extensively to linearize nonlinear failure criteria to avoid complex stress and strain analyses. YANG and YIN [10], LI [11], YANG et al [12], and LI and CHENG [13] proposed stability factors based on limit analysis theory for use in evaluating slope stability. ZHAO et al [14, 15] analyzed slope stability using a nonlinear failure criterion by combining limit analysis theory and a strength reduction technique. The single-tangent technique, according to which the whole sliding mass is assumed to be subjected to the same stress state, has typically been used in previous studies to obtain instantaneous tangent strength parameter values for use in analyzing the stability of slopes using nonlinear failure criteria. In reality, the normal stresses on different element boundaries are different, which leads to different stress states, and the curvature of the failure envelope implies that the instantaneous friction angle changes with the normal stress. Hence, the stress field of a sliding mass cannot be adequately simulated using the single-tangent technique.

Traditional slope stability limit analysis methods are normally based on the assumption that geomaterials are subject to an associated flow rule. In fact, the adoption of an associated flow rule results in overprediction for soil dilatancy, and the validity of the upper-bound limit analysis theorem for geomaterials subjecting to non-associated flow rules has been widely discussed in Refs. [16-19]. DRESCHER and DETOURNAY [16] made a substantial contribution to solving various stability problems for non-associative geomaterials by incorporating non-associated coaxial and non-coaxial flow rules and proposed a modified formula for the computation that considers dilation. KUMAR [17], WANG et al [18], and WANG and YIN [19] took this approach in studying the influence of the dilation coefficient on the slope safety factor by combining the limit analysis theorem with the strength reduction technique.

However, the combined influence of nonlinearity and dilation on slope stability has seldom been considered. YANG and HUANG [20] were the first to analyze the stability of a slope using a nonlinear M–C failure criterion and a nonassociated flow rule. ZHAO et al [21] analyzed the ultimate pullout capacity of horizontal shallow plate anchors with geomaterial nonlinearity and dilation taken into consideration. These studies, however, had the following limitations: 1) using a stability factor N_s alone as an index for evaluating slope stability is inconvenient in engineering practice; 2) dividing the sliding mass into vertical slices is not conducive to building potential slip surface flexibly; and 3) the single-tangent technique cannot be used to simulate the stress field of a sliding mass accurately.

The primary objective of the study described in this work is to analyze the stability of a homogeneous slope with a nonlinear M–C failure criterion and nonassociated flow rule by combining the strength reduction technique and the upper-bound limit analysis theorem. A virtual work equation was established for the collapse mechanism with nonlinear failure criterion and nonassociated flow rule by equating the rate of external work and the internal energy dissipation. The effects of nonlinear parameters in the failure criterion and the dilation coefficient in the nonassociated flow rule on slope stability and the potential slip surface were investigated. This study extended the previous studies by introducing a translational failure mechanism using the inclined-slices technique, adopting a multi-tangent method for performing a strict linearization of the nonlinear criterion, and employing the strength reduction technique to evaluate slope stability.

2 Basic principles of slope stability analysis

2.1 Nonlinear failure criterion and external tangent technique

A substantial amount of experimental data indicates that the failure envelopes of geotechnical materials are nonlinear, as widely discussed in previous studies. A nonlinear form of the Mohr–Coulomb (M–C) failure criterion has been widely used because of its simplicity and practicality. Using this nonlinear criterion, the nonlinear envelope of a group of Mohr circle can be expressed realistically as

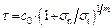                          (1)

where c₀ is the initial cohesion; σ_t is the axial tensile strength; σ_n and τ are the normal stress and shear stress on the shear plane, respectively; and m is a parameter for the nonlinearity. When m=1, Eq. (1) reduces to a linear M–C failure criterion. When the curvilinear relation given by Eq. (1) is plotted as shown in Fig. 1, the curve consistently passes through the point (0, c₀) and (-σ_t, 0), and m determines the curvature of the envelope.

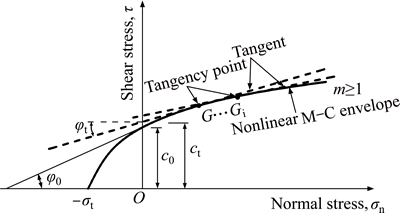
Fig. 1 Nonlinear failure criterion and its tangent line

The basic idea of the external tangent technique is to simplify the nonlinear M–C failure criterion to an instantaneous linear M–C yield criterion as illustrated in Fig. 1: with the given nonlinear M–C envelope curve, a line tangent to the curve is constructed at the tangency point G, and the values of the corresponding instantaneous shear strength parameters (c_t, φ_t) are obtained. The tangent function can be written as follows:

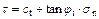                            (2)

where tan φ_t and c_t are the gradient and intercept of the tangent line, respectively, as shown in Fig. 1. These can be substituted for shear strength parameters obeying the tangential-line failure criterion. The equations for c_t and tan φ_t can be expressed as follows:

     (3)

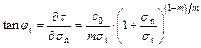             (4)

It should be noted that in Fig. 1, the strength at each point represented by the tangent line is always greater than or equal to the real strength at the point on the envelope curve. According to the upper-bound limit analysis theorem, an improvement in the yield strength of a material cannot decrease the ultimate load of a structure. Thus, the external tangent technique can be applied to slope limit analysis under the nonlinear M–C failure criterion.

The traditional single-tangent technique takes the strength at a tangent point as the geotechnical material strength parameter (c_t, φ_t), which converts the range of stress states in a sliding mass into a uniform stress state, resulting in a simple linearization of the nonlinear criterion. The curvature of the nonlinear failure envelope in Fig. 1, however, implies that the failure criterion for every point on the envelope curve can be substituted by the line tangent to the failure curve at that point and that the shear stress τ changes with the normal stress σ_n, resulting in different value of (c_t, φ_t) on different tangent points. Hence, it is necessary to introduce more external tangents to obtain a set of corresponding strength parameter (c_ti, φ_ti) for a strict linearization to the nonlinear M–C criterion as illustrated in Fig. 1. A more comprehensive description of this method can be found in the literature [12].

2.2 Nonassociated flow rule and modified shear strength parameter calculation

Geotechnical materials are subject to a nonassociated flow rule when the dilation angle is not equal to the friction angle. In general, for a nonassociated material, if the soil is subjected to a tangential-line failure criterion, the modified expressions given by DAVIS [5] for the equivalent shear strength parameters (c_t^*, φ_t^*) apply. DRESCHER and DETOURNAY [16] and MICHALOWSKI [22, 23] proposed a further modification to the shear strength parameter calculation for a nonassociated material subject to a tangential-line failure criterion. They proposed the following relations to take dilation into consideration:

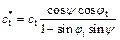                         (5)

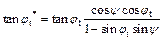                   (6)

where ψ is the dilation angle between the velocity vector and the discontinuity line. The dilation coefficient η can be expressed as η=ψ/φ. In theory, the dilation coefficient η varies within the range 0≤η≤1, where η=1 means that the material is subject to an associated flow rule. According to Eqs. (5) and (6), a nonassociated flow rule is introduced by using a modified friction angle 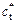and cohesion 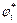or by upper-bound limit analysis. In this study, a nonlinear Mohr–Coulomb failure criterion was applied to a nonassociative material using the external tangent technique to analyze the combined influence of nonlinearity and dilation on slope stability. The values of the nonlinear shear strength parameters (c_t, φ_t ) can be obtained from Eqs. (3) and (4).

For a homogeneous slope with a nonassociated flow rule and nonlinear failure criterion, the modified shear strength parameters of the sliding mass are reduced to a new cohesive force c_f and an internal friction angle φ_f to make the slope reach a critical state using the strength reduction technique, as shown below:

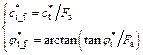                      (7)

where F_s is the shear strength reduction factor (safety factor) an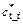d and 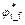are the modified shear strength parameters after reduction. The original shear strength parameters 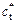and 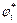can be obtained from Eqs. (5) and (6).

3 Upper-bound limit in slope stability analysis

3.1 Translational failure mechanism for arbitrary slip surface divided using inclined-slices technique

A typical translational failure mechanism for a homogeneous slope was constructed as shown in Fig. 2, in which the soil is subject to a nonlinear M–C failure criterion and nonassociated flow rule. The sliding mass of the slope is divided into n tilted slices with n-1 tilted interfaces and n bases using the inclined-slices technique. Assume that the slope height is H, β represents the slope toe angle, α represents the slope top angle, and γ represents the unit weight of the soil. Each of tilted slices moves in a rigid manner, and the tilted interface and base of each slice are plastic zones in which plastic energy dissipation occurs. The subscript i denotes the slice number, l_i is the length of the ith slice base, and α_i is the angle formed by the horizontal with the base of the ith slice, which is taken to be positive in the counterclockwise direction. The length of the interface between the ith slice and the (i+1)th slice is l_i,i+1.

Fig. 2 Translational failure mechanism for slope with inclined slices

The rectangular coordinates are defined with respect to O as the coordinate origin, as shown in Fig. 2. The section line of the slope links the coordinate points A₁, O′, and A₂-A_n+1, and the section of the sliding mass links the coordinate points B₁ and B_n+1. The x coordinate values of the starting point and endpoint of the slip surface, x_n+1 and x₁, respectively, can be obtained randomly, according to the corresponding boundary value range [x_Ln+1,x_Un+1], [x_L1,x_U1]. The corresponding coordinate values y_n+1 and y₁ can also be determined from the geometry of the slope. The upper- and lower-boundary value limits of the starting point and endpoint can be adjusted based on the condition of the slope.

3.2 Calculation of velocity field for multi-block systems

Figure 3 shows that adjacent slices will move with velocities of V_i and V_i+1 under an external force, according to the upper limit theorem, in which the velocity vector V_i inclines at an angle φ_ti* to the ith slice base and the velocity vector V_i,i+1 inclines at an angle φ*_ti,i+1 to the tilted interface [22, 24]. The vector difference of the velocity vectors V_i and V_i+1 will create the relative velocity V_i,i+1 between the adjacent ith and (i+1)th slices. It is not kinematically admissible for the adjacent slices to be separated or to overlap. Hence, a kinematically admissible velocity field V_i,i+1=V_i+1-V_i for the model can be obtained.

Based on the geometric relationships of the kinematically admissible velocity field, the following expression for the velocity of each slice can be derived:

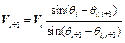                        (8)

The following expression for the relative velocity of the inclined interface between two adjacent slices can also be derived:

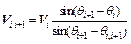                        (9)

where θ_i, θ_i+1 and θ_i,i+1 represent the angles between corresponding velocity vectors and the x axis, respectively. These angles are taken to be positive in the counterclockwise direction.

                             (10)

                         (11)

Fig. 3 Velocity field of adjacent slices

The lower slice impedes movement of the upper slice when θ_i<θ_i+1, as shown in Fig. 3(a). This situation is most commonly encountered.

                       (12)

The lower slice promotes movement of the upper slice when θ_i>θ_i+1, as shown in Fig. 3(b). This situation is rarely encountered.

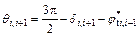                     (13)

In Eqs. (12) and (13), δ_i,i+1 is the angle of inclination of the interface between the ith slice and the (i+1)th slice and the vertical. This angle is taken to be positive in the clockwise direction (the clockwise rotation from the positive x direction to the positive y direction is defined as the positive direction for δ_i,i+1.

3.3 Energy dissipation rate and work of external forces

To simplify the calculation of the rate of energy dissipation, only the self-weight of the soil is taken into consideration in the upper-limit energy equilibrium equation. The calculation of the energy dissipation rate includes two components: the work that gravity does to the rigid block and the energy dissipation at the slice bases and tilted interfaces.

1) Internal energy dissipation rate

The internal energy dissipation rate is determined from the velocity discontinuity and consists of two components: the energy dissipation rate of the slice bases and the energy dissipation rate of the tilted interfaces.

The sum of the energy dissipation rates of the slice bases can be expressed as follows:

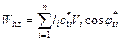                        (14)

where 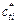represents the instantaneous cohesion of the ith slice base.

The sum of the energy dissipation rates of the tilted interfaces can be expressed as

        (15)

where represents the instantaneous cohesion of the interface between the ith and (i+1)th slices.

The total internal energy dissipation rate is the sum of the above two components:

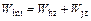                             (16)

2) Rate of external force

For the convenience of calculation, only the self-weight of the soil is taken into consideration. The external work is that done on the sliding mass by gravity. The total rate of external force is expressed as follows:

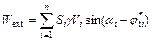                   (17)

where S_i is the area of the ith slice, which can be obtained from the geometry of the slope.

3.4 Calculation of slope safety factor

Introducing the strength reduction technique, the strength parameters are reduced by the same shear strength reduction factor F_s, thereby puts the sliding mass into a critical failure state. By the principle of virtual power, the energy dissipation rate is equal to the rate of external force, W_int=W_ext, i.e.:

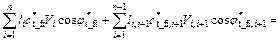
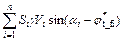                  (18)

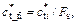
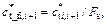
where 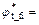arctan (tan φ^*_ti/F_s), and 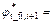arctan (tan φ^*_{t_i,i+1}/F_s). The 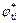and 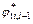terms in the equations for V_i and V_i,i+1 are replaced by φ^*_{t_ fi} and φ^*_{f_ti,i+1}. F_s is implied in the parameters c^*_{t_fi}, c^*_{t_fi,i+1}, φ^*_{t_fi}, and φ^*_{t_fi,i+1}. Equation (18) can be expressed as implicit function F_s, i.e., F_s (α_i, c^*_{t_fi}, c^*_{t_fi,i+1}, φ^*_{t_fi}, φ^*_{t_fi,i+1}, l_i , l_i,i+1).

Using the multi-tangent technique, a set of corresponding shear strength parameters (c_t, φ_t ) can be introduced for slope stability analysis. For given values of c₀, σ_t, and m, knowing the tangent instantaneous internal friction angle φ_t, the corresponding instantaneous cohesive force c_t can be obtained from Eq. (3). Therefore, the function F_s can be simplified to F_s (α_i, φ^*_{t_fi}, φ^*_{t_fi,i+1}, l_i, l_i,i+1). When φ_ti=φ_ti+1=φ_t and φ_ti+1,i+1=φ_ti+1,i+2=φ_t, the multi-tangent technique reduces to the traditional single-tangent technique. Therefore, the solution of the F_s-minimum-constrained nonlinear optimization problem can be simplified to F_s (α_i, φ^*_{t_f}, l_i,l_i,i+1). Nonlinear sequential quadratic programming (SQP) can be used to obtain an upper-bound solution for the slope safety factor F_s using the Fmincon function in the MATLAB software.

The above procedure for calculating the safety factor F_s is based on the condition that the slope height H is given. The slope stability factor of the slope can be defined as N_s=H_cr γ/c₀ for slope stability analysis with a nonlinear failure criterion and non-associated flow rule. The slope stability factor N_s can be obtained by treating H, which is implied in Eq. (18), as a dependent variable and treating F_s as an independent variable. Therefore, the solution of the H-minimum-constrained nonlinear optimization problem can be simplified to H (F_s, α_i, φ^*_{t_fi}, φ^*_{t_fi,i+1},l_i, l_i,i+1). When the slope safety factor F_s is 1.0, H equals the critical height H_cr. The slope stability factor N_s can be obtained by substituting H_cr into N_s=H_cr γ/c₀.

The following recommendations and guidelines were utilized in this work in identifying the critical surface:

1) The angle α₁ between the outer block of the sliding surface and the x axis is in the range of 0°–45°, based on experience.

2) In general, the critical slip surface of the slope should be a smooth, concave, and continuous curve that be expressed mathematically as follows:

0≤α_i+1-α_i≤Δα

Note that the value of Δα usually depends on specific circumstances and ranges from 1° to 10°, and note that α_n should be less than 90°.

3) When slope stability is studied on the basis of different failure criteria, the internal friction angle of slice φ_i and the equivalent friction angle of the inclined interface φ_i,i+1 should obey the following rule:

0≤φ_i, φ_i,i+1≤Δφ

Note that the value of Δφ depends on the failure criterion for the geotechnical material. In this work, the relation Δφ=arctan(c₀/mσ₀), which is discussed in detail in Ref. [21], was adopted.

4 Comparisons and analysis

4.1 Comparison of slope stability factor using nonlinear failure criterion and associated flow rule

Examples from Ref. [14] were selected to demonstrate the validity of the proposed method for analyzing the stability of slope using nonlinear M-C failure criterion.

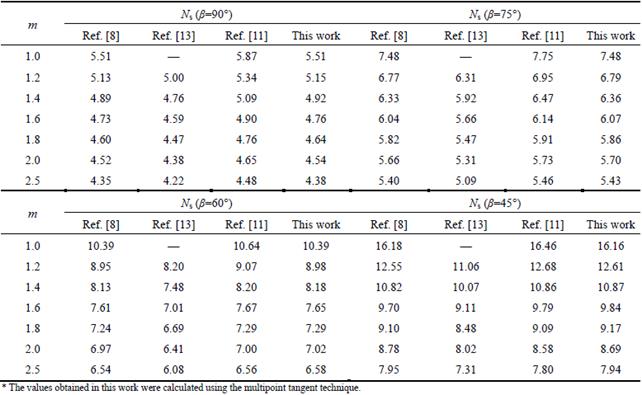
For the case of α=0°, γ=20 kN/m³, c₀=90 kN/m², σ_t=247.3 kN/m², and η=1.0, values of the slope stability factor N_s reported in various studies [8, 11, 13] were compared, as shown in Table 1 for m=1.0-2.5 and slope angle β=45°-90°

Table 1 shows that the slope stability factor results obtained by the proposed method show good agreement with the results of previous research, with relative errors less than 5.0%, which demonstrates that the proposed method is appropriate for slope stability limit analysis with nonlinear M-C failure criterion.

4.2 Comparison of slope safety factors using linear failure criterion and nonassociated flow rule

An embankment slope example from the literature was selected to demonstrate the validity of the proposed method for slope stability analysis using a nonassociated flow rule. The parameters in this example are as follows: the slope height H=8 m, the slope (horizontal: vertical) is 2:1, α=0°, γ=19.6 kN/m³, φ=30°, c varies from 5 to 20 kPa, and the nonlinear parameter m=1. Table 2 shows a comparison of the safety factors (F_s) values calculated by WANG et al [18] with those calculated using the proposed method.

Table 2 shows that the F_s values calculated using the proposed method are similar to those calculated by Wang et al [18], with relative errors less than 6.8%. The results of the comparison show that the proposed method is an effective method for evaluating slope stability with a nonassociated flow rule. Meanwhile, the vast majority of Δ are greater than zero, which means the present method a more conservative method. Furthermore, Δ increases with decreasing η, that means the present method is more specifically suited to evaluate slope stability considering the nonassociated flow rule.

4.3 Comparison of slope safety stability using nonassociated flow rule and nonlinear failure criterion

Table 1 Variation of slope stability factor N_s with nonlinear parameter m

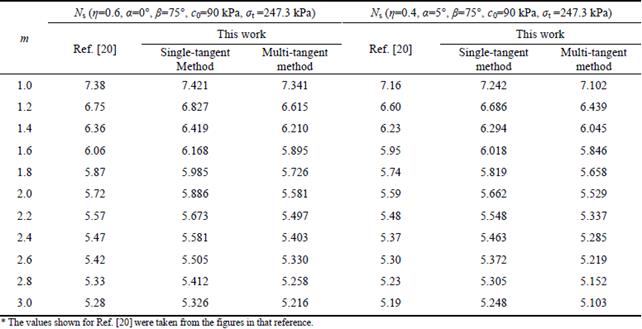
An embankment slope example from Ref. [20] was selected to demonstrate the validity of the proposed method for analyzing slope stability using a nonassociated flow rule. The parameters in this example are as follows: slope angle β=75°, c₀=90kPa, and σ_t=247.3 kPa. The calculated slope safety factors F_s are compared in Table 3 for η=0.6 and slope angle α=0° and for η=0.4 and slope angle α=5°, with the nonlinear parameter m varying from 1.0 to 3.0.

Table 3 shows that the slope stability factors obtained using the proposed method show good agreement with the values calculated by YANG and HUANG [20], which demonstrates that the proposed method is appropriate for slope stability limit analysis using the nonlinear failure criterion and nonassociated flow rule. The slope stability safety factors N_s calculated using the multi-tangent inclined-slices technique are smaller than those calculated using the traditional single-tangent inclined-slices technique and those calculated by YANG and HUANG [20] using the upper-bound limit analysis method. The results show that the multi-tangent technique is a safe and effective method for use in slope stability analysis with a nonlinear failure criterion and nonassociated flow rule. Therefore, the safety factor values reported in the next section were obtained using the multi-tangent technique.

Table 2 Variation of factor of safety F_s with dilation coefficient η

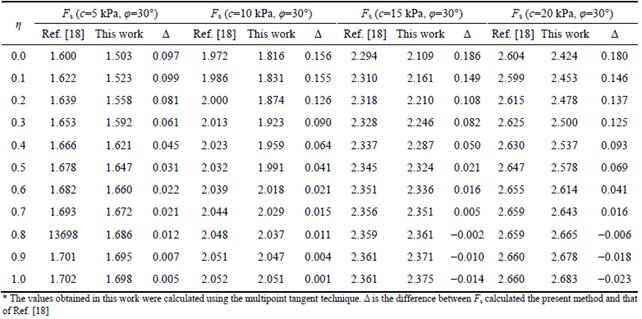
Table 3 Variation of stability factor N_s with dilation coefficient η and nonlinear parameter m

5 Influence of nonassociated flow rule and nonlinear failure criterion on slope stability

5.1 Effect of associated flow rule and nonlinear failure criterion on slope stability

To investigate how the slope stability is influenced by nonlinear M-C failure criterion with an associated flow rule (dilation coefficient η=1), an example of a simple homogeneous slope with a height of 25 m and angle α=5° was considered. The other physical parameters of the soil were as follows: γ=20 kN/m³, c₀= 90 kN/m², and σ_t=247.3 kN/m². The effects of the nonlinear parameter m varying from 1.0 to 3.0 and the slope angle β varying from 45° to 90° on the value of the slope safety factor F_s and the corresponding average

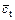
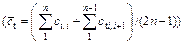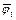
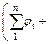
values of the instantaneous shear strength parameters and 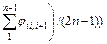are illustrated in Fig. 4.

Figure 4 shows that the nonlinear parameter m has a significant effect on the slope safety factor F_s and the average values of the instantaneous shear strength parameters. The F_s value and the average value of the instantaneous cohesion φ_t decrease rapidly as the nonlinear parameter m increases, and the average value of the instantaneous internal friction angle c_t increases gradually.

A simple slope with α=10°, β=45°, H=18 m, γ=20 kN/m³, c₀=90 kN/m², and σ_t=247.3 kN/m² was next considered. Values of 1.0, 2.0, and 3.0 were considered for the nonlinear parameter m. The geotechnical materials of the slope were assumed to be subjected to an associated flow rule. The effect of a nonlinear failure criterion on the critical slip surface of the slopes is illustrated in Fig. 5.

Figure 5 shows that the failure area of the slope increases as the nonlinear parameter m increases

5.2 Effect of nonassociated flow rule and nonlinear failure criterion on slope stability

To investigate how the slope stability is influenced by nonlinear M-C failure criterion with a nonassociated flow rule, a simple homogeneous slope with H=20 m, α=5°, β=60°, γ=20 kN/m³, c₀=90 kN/m², and σ_t=247.3 kN/m² was considered. The effects of varying the nonlinear parameter m from 1.0 to 3.0 and varying the dilation coefficient 0 to 1.0 on the slope safety factor F_s and the corresponding average values of the shear strength parameters 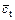and 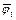are illustrated in Fig. 6.

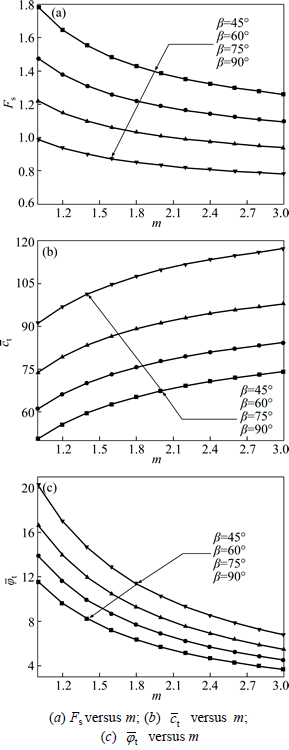
Fig. 4 Effect of nonlinear parameter m on average value of instantaneous shear strength parameters and slope safety factor F_s under different slope angle β

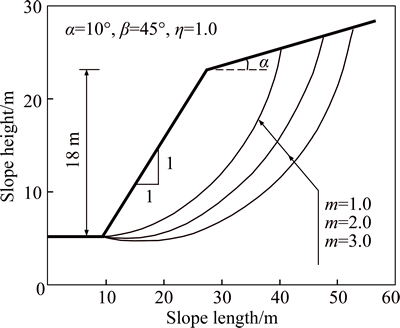
Fig. 5 Effect of nonlinear failure criterion on critical slip surface of slopes

Fig. 6 Effect of nonlinear parameter m on mean value of instantaneous shear strength parameters and slope safety factor F_s under different dilation coefficient η

Figure 6 shows that the dilation coefficient η has little effect on the average instantaneous internal friction angle 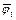but a large effect on the average instantaneous cohesion 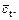The value of F_s and the average value of the instantaneous cohesion c_t increase as the dilation coefficient η increases. The nonlinear parameter m has a large effect on the value of F_s and the average values of the shear strength parameters. The value of F_S and the average value of the internal friction angle φ_t decrease gradually as the nonlinear parameter m increases, but the average value of the instantaneous cohesion c_t increases relatively rapid when m increases from 1.0 to 2.0 but slowly afterwards .

Two simple slopes with α=5°, β=30°, H=40 m, γ= 20 kN/m³, c₀=90 kN/m², and σ_t=247.3 kN/m² were next considered. Using the same calculation parameters mentioned above, the other physical parameters of the two simple slopes are, respectively, m=1.5 and η=0.0, 0.5, and 1.0 and m=1.0, 2.0, and 3.0 and η=0.5. The effects of the nonlinear failure criterion and nonassociated flow rule on the critical slip surfaces of the slopes are illustrated in Fig. 7.

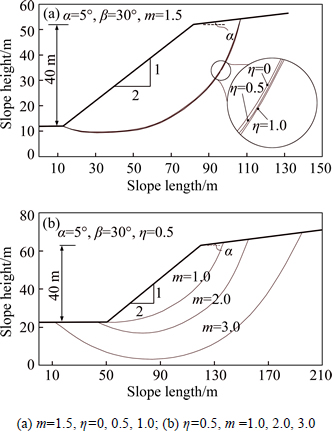
Fig. 7 Influences of nonlinear failure criterion and nonassociated flow rule on critical slip surface of slopes

Figures 7(a) and (b) show that for the given values of the nonlinear parameter m, the failure areas of the slopes increase slightly as the value of the nonassociated parameter η. For the given values of the nonassociated parameter -η, the failure areas of the slopes increase rapidly as the value of the nonlinear parameters m increases.

6 Conclusions

1) Comparative analysis revealed that the results obtained using the proposed method show good agreement with previous research results, which demonstrates the rationality and reliability of the proposed method. The slope stability safety factors F_s calculated using the multi-tangent inclined-slices technique are smaller than those obtained using the traditional single-tangent inclined-slices technique. The results show that the multi-tangent inclined-slices technique is a safe and effective method for use in slope stability analysis.

2) The results of this study indicate that nonlinear M-C failure criterion and nonassociated flow rule significantly affect slope stability. The dilation coefficient η has little effect on the average instantaneous friction angle but a large effect on the average instantaneous cohesion. The slope safety factor F_s and the average value of c_t increase significantly as the dilation coefficient η increases, and the average value of the instantaneous friction angle decreases slightly. The nonlinear parameter m has a large effect on the slope safety factor F_s and the average values of the shear strength parameters. The slope safety factor F_s and the average value of the instantaneous friction angle φ_t decrease rapidly with increasing m, and the average value of c_t increases gradually. Because of the intrinsic characteristics of the upper-limit failure mechanism, the average instantaneous friction angle decreases rapidly with increasing m, and the failure area of the slope increases significantly.

References

[1] CHEN W F, LIU X L. Limit analysis in soil mechanics [M]. Amsterdam: Elsevier Science, 1990.

[2] MAKSIMOVIC M. Nonlinear failure envelope for soils [J]. J Geotech Eng, ASCE, 1989, 115(4): 581-586.

[3] BAKER R. Nonlinear Mohr envelopes based on triaxial data [J]. J Geotech Geoenviron Eng, ASCE, 2004, 130(5): 498-506.

[4] AGAR J G, MORGENSTERN N R, SCOTT J. Shear strength and stress-strain behavior of Athabasca oil sand at elevated temperatures and pressure [J]. Can Geotech J, 1987, 24(1): 1-10.

[5] DAVIS E H. Theories of plasticity and the failure of soil masses [C]// LEE I K. Soil Mechanics: Selected topics. London: Butterworth, 1968: 341-380.

[6] ZIENKIEWICZ O C, HUMPHESON C, LEWIS R W. Associated and non-associated visco-plasticity and plasticity in soil echanics [J]. Géotechnique, 1975, 25: 671-689.

[7] de BORST R, VERMEER P A. Possibilities and limitations of finite elements for limit analysis [J]. Geotechnique, 1984, 34(2): 199-210.

[8] ZHANG X J, CHEN W F. Stability analysis of slopes with general nonlinear failure criterion [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1987, 11(1): 33-50.

[9] COLLINS I F, GUNN C I, PENDER M J, YAN W. Slope stability analyses for materials with nonlinear failure envelope [J]. Int J Numer Anal Methods Geomech, 1988, 12(6): 533-550.

[10] YANG X L, YIN J H. Slope stability analysis with nonlinear failure criterion [J]. Journal of Engineering Mechanics, ASCE, 2004, 130(3): 267-273.

[11] LI X. Finite element analysis of slope stability using a nonlinear failure criterion [J]. Computers and Geotechnics, 2007, 34(3): 127-136.

[12] YANG X L, YANG Z H, LI Y X, LI S C. Upper bound solution for supporting pressure acting on shallow tunnel based on modified tangential technique [J]. Journal of Central South University of Technology, 2013, 20(12): 3676-3682.

[13] LI D H, CHENG Y M. Lower bound limit analysis using nonlinear failure criteria [C]// 2012 International Conference on Structural Computation and Geotechnical Mechanics [J]. Procedia Earth and Planetary Science, 2012, 5: 170-174.

[14] ZHAO L H, LI L, YANG F, LUO Q. Upper bound analysis of slope stability with nonlinear failure criterion based on strength reduction technique [J]. Journal of Central South University of Technology, 2010, 17(4): 836-844.

[15] ZHAO L H, YANG F, ZHANG Y B, DAN H C, LIU W Z. Effects of shear strength reduction strategies on safety factor of homogeneous slope based on a general nonlinear failure criterion [J]. Computers and Geotechnics, 2015, 63: 215-228.

[16] DRESCHER A, DETOURNAY C. Limit load in translational failure mechanisms for associative and non-associative materials [J]. Géotechniqu, 1993, 43(3): 443-456.

[17] KUMAR J. Stability factors for slopes with nonassociated flow rule using energy consideration [J]. Int J Geomech, 2004, 4(4): 264-272.

[18] WANG Y J, YIN J H, LEE C F. The influence of a non-associated flow rule on the calculation of the factor of safety of soil slopes [J]. Int J Numer Anal Meth Geomech, 2001, 25(13): 1351-1359.

[19] WANG Y J, YIN J H. Wedge stability analysis considering dilatancy of discontinuities [J]. Rock Mechanics and Rock Engineering, 2002, 35(2): 127-137.

[20] YANG X L, HUANG H. Slope stability analysis considering joined influences of nonlinearity and dilation. [J]. Journal of Central South University of Technology, 2009, 16(2): 292-296.

[21] ZHAO L H, LI L, YANG F, LIU X. Joined the influences of nonlinearity and dilation on the ultimate pullout capacity of horizontal shallow plate anchors by energy dissipation method [J]. International Journal of Geomechanics, 2010, 11(3): 195-201.

[22] MICHALOWSKI R L. Slope stability analysis: A kinematical approach [J]. Géotechnique, 1995, 45(2): 283-293.

[23] MICHALOWSKI R L. Limit analysis in geotechnical engineering [C]// 16th Int Conf on Soil Mechanics and Geotechnical Engineering (16th ISSMGE), TC-34 Rep. 2005(5): 3679-3684.

[24] DONALD I, CHEN Z Y. Slope stability analysis by the upper bound approach: Fundamentals and methods [J]. Canadian Geotechnical Journal, 1997, 34(6): 853-862.

(Edited by YANG Hua)

Cite this article as:

TANG Gao-peng, ZHAO Lian-heng, LI Liang, CHEN Jing-yu. Combined influence of nonlinearity and dilation on slope stability evaluated by upper-bound limit analysis [J]. Journal of Central South University, 2017, 24(7): 1602-1611.

Foundation item: Projects(51208522, 51478477) supported by the National Natural Science Foundation of China; Project(2012122033) supported by the Guizhou Provincial Department of Transportation Foundation, China; Project(CX2015B049) supported by the Scientific Research Innovation Project of Hunan Province, China

Received date: 2015-09-02; Accepted date: 2016-03-22

Corresponding author: ZHAO Lian-heng, Professor; Tel: +86-13755139425; E-mail: zlh8076@163.com

Abstract: The combined influence of nonlinearity and dilation on slope stability was evaluated using the upper-bound limit analysis theorem. The mechanism of slope collapse was analyzed by dividing it into arbitrary discrete soil blocks with the nonlinear Mohr–Coulomb failure criterion and nonassociated flow rule. The multipoint tangent (multi-tangent) technique was used to analyze the slope stability by linearizing the nonlinear failure criterion. A general expression for the slope safety factor was derived based on the virtual work principle and the strength reduction technique, and the global slope safety factor can be obtained by the optimization method of nonlinear sequential quadratic programming. The results show better agreement with previous research result when the nonlinear failure criterion reduces to a linear failure criterion or the non-associated flow rule reduces to an associated flow rule, which demonstrates the rationality of the presented method. Slope safety factors calculated by the multi-tangent inclined-slices technique were smaller than those obtained by the traditional single-tangent inclined-slices technique. The results show that the multi-tangent inclined-slices technique is a safe and effective method of slope stability limit analysis. The combined effect of nonlinearity and dilation on slope stability was analyzed, and the parameter analysis indicates that nonlinearity and dilation have significant influence on the result of slope stability analysis.