J. Cent. South Univ. Technol. (2008) 15: 774-778
DOI: 10.1007/s11771-008-0143-3![]()
Improvement of Prandtl mixing length theory and application in modeling of turbulent flow in circular tubes
LUO Xiao(罗 潇), LIU Ping-le(刘平乐), LUO He-an(罗和安)
(College of Chemical Engineering, Xiangtan University, Xiangtan 411105, China)
Abstract:
In order to correctly predict tube cross section time-smoothed velocity distribution, friction factor and mass transfer behavior, two models for turbulent flow in circular tubes based on classical Prandtl mixing length theory and a modified mixing length were established. The results show that the modified mixing length includes the introduction of a damping function for the viscous sublayer and the second-order derivative to approximate eddy velocity. The calculated dimensionless time-smoothed velocity from the model based on Prandtl mixing length is much better than the result from the concept of eddy viscosity. The calculated eddy viscosity from the model based on modified mixing length is much better than the result from the model based on the classical Prandtl mixing length theory. And the friction factor calculated from the model based on the modified mixing length agrees well with the reported empirical relationships.
Key words:
turbulent flow; Prandtl mixing length; time-smoothed velocity; eddy viscosity; friction factor;
1 Introduction
Turbulent flow is important in all technical application and engineering practice. Till now, semi-empirical method has been widely used to deal with turbulent flow. Although computational fluid dynamics undergoes rapid development, direct simulation of flows is restricted to very simple geometries and low Reynolds number[1-6]. Development of turbulence model is therefore still an important task and even some semi-empirical means such as the eddy viscosity or Prandtl mixing length are very helpful to dealing with many problems in engineering practice due to their simplicity[7-10]. For instance, FRISCH[11] expressed Reynolds stress for turbulent flow in circular tubes by the eddy viscosity or the Prandtl mixing length.
Although the conception of eddy viscosity is commonly used, it should be in fact an empirical means because it is only from an external analogy of the molecular viscosity of fluid[11]. In addition, the coefficient of eddy viscosity μt is not a constant like the molecular viscosity, and it should be a function of the overall and local Reynolds numbers. As an example, REICHARDT[12] proposed an equation of eddy viscosity coefficient for high turbulence in tubes.
Prandtl mixing length theory comes from the assumption that eddies’ movement in fluid is similar to molecules’ movement in low-density gas[13]. This is a more fundamental and acceptable analogy compared with eddy viscosity though it is not very good, and the mixing length (l) should also be determined by experiment. However, the Prandtl mixing length mainly succeeds in dealing with some extreme cases such as wall turbulence and free turbulence[14]. Hence, some modification and improvement of Prandtl mixing length were attempted in this work. Tube turbulent flow models based on the modified Prandtl mixing length were established to focus on time-smoothed velocity distribution, eddy viscosity and friction factor.
2 Modeling of turbulent flow in circular tubes
2.1 Model based on Prandtl mixing length theory (Model 1)
Reynolds stress for turbulent flow in circular tubes can be expressed by the eddy viscosity or the Prandtl mixing length[11]
![]() (1)
(1)
An equation of eddy viscosity coefficient for high turbulence in tube is[12]:

Commonly, the shearing stress of Newtonian fluid for turbulent flow can be described as the sum of the molecular and eddy’s parts:
Combining Eqn.(1) with Eqn.(3) gives a model of time-smoothed velocity for turbulent flow in circular tubes:
The boundary conditions and constrained conditions are
![]() (5)
(5)
where
![]() (6)
(6)
t and tw represent the shearing stress of liquid and the shearing stress on the wall; R, ![]() and r represent the tube radius, the dimensionless radius and the radial distance from the tube center; u, u′,
and r represent the tube radius, the dimensionless radius and the radial distance from the tube center; u, u′, ![]()
![]()
![]() and
and ![]() represent the time-smoothed velocity, the axial pulse velocity, the friction velocity, the dimensionless time-smoothed velocity, the average velocity of tube cross section and radial pulse velocity respectively; l, l, f, r and m represent the mixing length, the dimensionless mixing length, the dimensionless radial distance, the density and the viscosity of liquid respectively.
represent the time-smoothed velocity, the axial pulse velocity, the friction velocity, the dimensionless time-smoothed velocity, the average velocity of tube cross section and radial pulse velocity respectively; l, l, f, r and m represent the mixing length, the dimensionless mixing length, the dimensionless radial distance, the density and the viscosity of liquid respectively.
Eqn.(4) is the model of time-smoothed velocity profile for turbulent flow in circular tubes based on Prandtl mixing length theory, denominated as Model 1, where the dimensionless mixing length (λ) is a key parameter that has been found to be not a universal constant but a function of position. PRANDTL proposed an expression for the mixing length in wall turbulence as follows:
![]() (7)
(7)
That is, the mixing length of eddies is proportional to the distance from the wall in the region near the wall except the viscous sublayer[15]. Additionally, κ in Eqn.(7) has been found to be a constant of about 0.4 under the condition that Reynolds number is large enough. As mentioned above, Eqn.(7) in fact, cannot be used in the region far from the wall to the center of the tube. Hence, a relationship for the mixing length covering the whole region except for the viscous sublayer was proposed in Ref.[16]:
There are numerous attempts to extend the equations of mixing length to include the viscous sublayer, multiplying the mixing length by a damping function. By using an analogy with the laminar flow on an oscillating flat plate, ABBOTT et al[17] obtained a similar expression for damping function based on the unsteady one-dimensional momentum equation and the unsteady one-dimensional vorticity equation respectively:
where A is an empirical constant of about 26, which is called damping-length constant. In fact, the damping- length constant A is expected to vary somewhat with flow conditions. Later, in order to make the turbulent viscosity proportional to (1-f)3 at f=1, HANNA et al[18] proposed the following modification for Eqn.(9):
From Eqns.(8) and (9) or Eqn.(10), it follows that
![]() (11)
(11)
Combining Eqns.(4) with (11) gives a profile of the time-smoothed velocity for turbulent flow in circular tubes. In latish computation, it can be found that either of damping function Eqn.(9) or Eqn.(10) is optional since their effect on computing results is almost the same.
2.2 Model based on modified mixing length (Model 2)
According to Prandtl mixing length theory, Eqn.(1), the eddy viscosity coefficient can be rewritten as
![]() (12)
(12)
where ![]() represents eddy viscosity coefficient. It can be seen from the equation that the eddy viscosity at the center of a circular tube will be zero because of the symmetry of flow. However, the eddy viscosity at the center should not be zero according to the conception or the experiment. This inconsistency may be caused mainly by that Prandtl only took the first-order derivative to approximate the eddy velocity. Thus, a simple way to modify Prandtl mixing length theory is to utilize the second-order derivative to approach the eddy velocity:
represents eddy viscosity coefficient. It can be seen from the equation that the eddy viscosity at the center of a circular tube will be zero because of the symmetry of flow. However, the eddy viscosity at the center should not be zero according to the conception or the experiment. This inconsistency may be caused mainly by that Prandtl only took the first-order derivative to approximate the eddy velocity. Thus, a simple way to modify Prandtl mixing length theory is to utilize the second-order derivative to approach the eddy velocity:
Eqn.(13) is an expression of the modified mixing length. Combining this equation with Eqn.(3), it follows a time-smoothed velocity profile for turbulent liquid flow in circular tubes, denominated as Model 2:
The boundary and constrained conditions are Eqn.(5) and
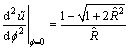 (15)
(15)
where
![]() (16)
(16)
Obviously, λ in Eqn.(8) is not suitable for this modified model. This is because the relationship comes from correlating the measured data of ![]() and the time-smoothed velocity with Eqn.(1). That is, the expression of λ for the modified model should be obtained from correlating the measured data with Eqn.(13). Since the data are unavailable, Eqn.(8) is reconstructed to adapt to the modified model.
and the time-smoothed velocity with Eqn.(1). That is, the expression of λ for the modified model should be obtained from correlating the measured data with Eqn.(13). Since the data are unavailable, Eqn.(8) is reconstructed to adapt to the modified model.
From Eqns.(1) and (13), it follows that
![]() (17)
(17)
where λ1 and λ2 are denominated as the mixing lengths respectively for Model 1 and Model 2, respectively. The former is known as Eqn.(8), while the latter can be calculated from Eqn.(17) where the derivatives of velocity are substituted by the calculated results from Model 1. In this way, the dimensionless mixing length for Model 2 can be expressed as
![]() (18)
(18)
In order to be convenient for discussion, Model 1, Eqn.(4), together with Eqn.(8) is named as Model 1(a); Model 1 together with Eqn.(11) is denominated as Model 1(b); Model 2, Eqn.(14), together with Eqn.(11) is called as Model 2(a); Model 2, together with Eqn.(18), constructs Model 2(b).
3.1 Profile of dimensionless time-smoothed velocity
Fig.1 shows the comparison between the models of this work and the empirical equation of LIN et al[19] under the condition that Re=1×106 for circular tubes. It can be found that Model 1(a) is quite different from the empirical profile, while Model 1(b) agrees well with the empirical data, which indicates that the effect of the mixing length in the viscous sublayer is very important.
Model 2(a), the modified mixing length model with
a borrowed expression of the mixing length, is still departure from the empirical relationship. However, Model 2(b), the modified model with the reconstructed relationship of mixing length is similar to Model 1(b) and also agrees well with the empirical profile.
Curve 6 in Fig.1 is the result of the model based on the method of eddy viscosity in Eqn.(2). Compared with the empirical profile, there exist obvious differences. This means that the application of Prandtl mixing length theory in tube turbulent flow is much better than that of the concept of eddy viscosity.
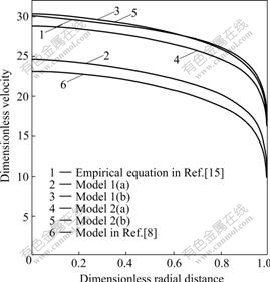
Fig.1 Velocity profiles from Models and empirical equation at Re=1×106
The behaviors when Reynolds number is larger than 4 000 are similar to the above cases.
3.2 Dimensionless eddy viscosity
Fig.2 compares the calculated eddy viscosity profiles from Model 1(b) and Model 2(b) with the empirical equation of REICHARDT (Eqn.(8)) at Re=1×106. It can be found that Model 1(b) and Model 2(b) agree well with the empirical equation of REICHARDT not very far from the tube wall, but are quite different from REICHARDT’s equation nearby the center of a tube. Especially, the eddy viscosity calculated from Model 1(b) is zero at the center, which is not in accordance with the fact. The reason is discussed in Section 2.2. Generally, Model 2(b) is better than Model 1(b) in prediction of eddy viscosity.
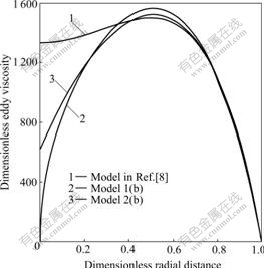
Fig.2 Eddy viscosity profiles from models and REICHARDT’s equation at Re =1×106
It can be seen from Fig.1 that Model 1(b) and Model 2(b) are nearly the same in prediction of the time-smoothed velocity. However, they are very different in prediction of the eddy viscosity near the center. This indicates that the influence of eddy viscosity in the center region can be ignored.
3.3 Friction factor for circular tubes
The definition of the friction factor in tubes is as follows[14]:
![]() (19)
(19)
where ![]() represents friction factor; D and L represent diameter and distance of tube; and P represents pressure. Fig.3 gives the friction factors from the models developed by this work and from the empirical equation of BARENBLATT[20].
represents friction factor; D and L represent diameter and distance of tube; and P represents pressure. Fig.3 gives the friction factors from the models developed by this work and from the empirical equation of BARENBLATT[20].
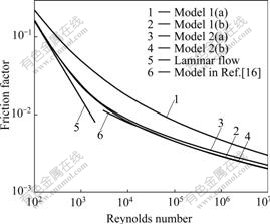
Fig.3 Friction factor for smooth tubes from models and empirical equation
Firstly, for the turbulent flow (Re>4 000) in tubes, Model 1(a) is quite different from the empirical equation of BARENBLATT, while Model 1(b) is in good agreement with it, especially when Re is larger than 1×104. This testifies again that the influence of the viscous sublayer is very significant. Secondly, Model 2(a) is still a little different from the empirical equation of BARENBLATT, Model 2(b) agrees well with BARENBLATT’s empirical equation, and almost the same as Model 1(b).
It is interesting that Model 1(b) and 2(b) are close to the theoretical equation of laminar flow in circular tubes at very low Reynolds number. This may be caused by damping function that involves the effects of viscous sublayer on the mixing length and Reynolds number.
4 Conclusions1) The modified mixing length overcomes the shortcoming of Prandtl mixing length theory that gives a zero value of turbulent viscosity at the center of circular tubes. Two models of time-smoothed liquid velocity for turbulent flow in tubes based on Prandtl mixing length theory and the modified mixing length are developed. According to the comparison of the models based on Prandtl mixing length theory with the empirical expression of time-smoothed velocity in tubes, it shows that the model based on Prandtl mixing length theory is much better than the method of eddy viscosity.
2) The modified mixing length includes the introduction of a damping function for the viscous sublayer and the second-order derivative to approximate eddy velocity. The model based on the modified mixing length agrees well with the empirical relationships reported in literature for predicting the time-smoothed velocity, eddy viscosity and friction factor for turbulent flow in tubes. Particularly, the agreement for the friction factor also exists at very low Reynolds number. This indicates that the effect of the viscous sublayer on turbulent flow in tubes is very important for momentum transfer and perhaps for heat and mass transfer.
References[1] ZHANG Zhao-shun, CUI Gui-xiang, XU Chun-xiao. Theory and modeling of turbulence [M]. Beijing: Tsinghua University Press, 2005.
[2] HE S, JACKSON J D. A study of turbulence under condition of transient flow in a pipe [J]. Journal of Fluid Mechanics, 2000, 408: 1-38.
[3] MORSI Y S M, HOLLAND P G, CLAYTON B R. Prediction of turbulent swirling flows in axisymmetric annuli [J]. Applied Mathematical Modelling, 1996, 19(10): 613-620.
[4] PRIYMAK V G, MIYAZAKI T. Accurate navier-stokes investigation of transitional and turbulent flows in a circular pipe [J]. Journal of Computational Physics, 1998, 142(2): 370-411.
[5] COTTON M A. Resonant response in periodic turbulent flows: Computations using a k-e eddy viscosity model [J]. Journal of Hydraulic Research, 2007, 45(1): 54-61.
[6] CHANDESRIS M, SERRE G, SAGAUT P. A macroscopic model for flow in porous media suited for channel, pipe and rod bundle flows [J]. International Journal of Heat and Mass Transfer, 2006, 49(15/16): 2739-2750.
[7] CRUZ D O A, PINHO F T. Turbulent pipe flow predictions with a low Reynolds number k-e model for drag reducing fluids [J]. Journal of Non-Newtonian Fluid Mechanics, 2003, 114(2/3): 109-148.
[8] RICE M, HALL J, PADADAKIS G, YIANNESKIS M. Investigation of laminar flow in a stirred vessel at low Reynolds numbers [J]. Chemical Engineering Science, 2006, 61(9): 2762-2770.
[9] FIOFFMAN J, JOHNSON C. A new approach to computational turbulence modeling [J]. Computer Methods in Applied Mechanics and Engineering, 2006, 195(23/24): 2865-2880.
[10] IIZUKA S, KONDO H. Large-eddy simulation of turbulent flow over complex terrain using modified static eddy viscosity models [J]. Atmospheric Environment, 2006, 40(5): 925-935.
[11] FRISCH U. Turbulence [M]. London: Cambridge University Press, 1995.
[12] REICHARDT H. Complete representation of a turbulent velocity distribution in smooth tubes [J]. Journal of Applied Mathematics and Mechanics, 1951, 31(7): 208-219.
[13] DJORDJEVIC V D. A higher-order asymptotic theory for fully developed turbulent flow in smooth pipes [J]. Journal of Engineering Mathematics, 1998, 33(3): 237-250.
[14] BIRD R B, STEWART W E, LIGHTFOOT E N. Transport phenomena [M]. New York: John Wiley & Sons Inc, 2002.
[15] ZYABRIKOV V V, LOITSYANSKII L G. The damping factor in the theory of Prandtl mixing length [J]. Fluid Dynamics, 1987, 22(5): 695-701
[16] BRADSHAW P. Turbulence [M]. Heidelberg: Springer-Verlag, 1976.
[17] ABBOTT D E, WALKER J D A, YORK R E. Numerical solution of turbulent boundary layers approaching separation [C]// ROBERT D R. Proceedings of the Fourth International Conference on Numerical Methods in Fluid Dynamics. Heidelberg: Springer-Verlag, 1975: 34-39.
[18] HANNA O T, SANDALL O C, MAZET P R. Heat and mass transfer in turbulent flow under conditions of drag reduction [J]. American Institute of Chemical Engineering Journal, 1981, 27(4): 693-697.
[19] LIN C S, MOULTON R W, PUTNAM G L. Mass transfer between solid wall and fluids streams [J]. Industrial Engineering Chemistry, 1953, 45(3): 636-640.
[20] BARENBLATT G I. Scaling, self-similarity, and intermediate asymptotics [M]. London: Cambridge University Press, 1996.
Foundation item: Project(20736009) supported by the National Natural Science Foundation of China; Project(07JJ6017) supported by the Natural Science Foundation of Hunan Province, China
Received date: 2008-04-16; Accepted date: 2008-05-30
Corresponding author: LIU Ping-le, Professor, PhD; Tel: +86-732-8293545; E-mail: liupingle@xtu.edu.cn
(Edited by CHEN Wei-ping)
Abstract: In order to correctly predict tube cross section time-smoothed velocity distribution, friction factor and mass transfer behavior, two models for turbulent flow in circular tubes based on classical Prandtl mixing length theory and a modified mixing length were established. The results show that the modified mixing length includes the introduction of a damping function for the viscous sublayer and the second-order derivative to approximate eddy velocity. The calculated dimensionless time-smoothed velocity from the model based on Prandtl mixing length is much better than the result from the concept of eddy viscosity. The calculated eddy viscosity from the model based on modified mixing length is much better than the result from the model based on the classical Prandtl mixing length theory. And the friction factor calculated from the model based on the modified mixing length agrees well with the reported empirical relationships.
- Improvement of Prandtl mixing length theory and application in modeling of turbulent flow in circular tubes



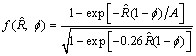 (
(