J. Cent. South Univ. (2017) 24: 2496-2503
DOI: https://doi.org/10.1007/s11771-017-3662-y

Limit equilibrium analysis for stability of soil nailed slope and optimum design of soil nailing parameters
DENG Dong-ping(邓东平), LI Liang(李亮), ZHAO Lian-heng(赵炼恒)
School of Civil Engineering, Central South University, Changsha 410075, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2017
Abstract:
Reinforcement of slopes using soil nailing can effectively improve slope stability, and it has been widely used in upgrading cut slopes. Based on the assumptions of stresses on the slip surface, a new method for analyzing the stability of a slope reinforced with soil nails was established in the limit equilibrium theory framework, by considering that slope sliding occurs owing to shear failure of the slip surface, which subjects to Mohr–Coulomb (M–C) strength criterion. Meanwhile, in order to easily analyze the stability of a soil nailed slope in actual engineering and facilitate optimum design of parameters for soil nailing, factor of safety (FOS) contour curve charts were drawn on the basis of the established linear proportional relationship between the spacing of soil nails and slope height, and the length of soil nails and slope height. Then, by analyzing and verifying the results obtained from classic examples, some conclusions can be got as follows: 1) The results obtained from the current method are close to those obtained from the traditional limit equilibrium methods, and the current method can provide a strict solution for the slope FOS as it satisfies all the static equilibrium conditions of a sliding body, thus confirming the feasibility of the current method; 2) The slope FOS contour curve charts can be used not only to reliably analyze the stability of a soil nailed slope, but also to design optimally the parameters of soil nailing for the slope with a certain safety requirement.
Key words:
slope stability; soil nailing; limit equilibrium; factor of safety contour curve; optimum design;
1 Introduction
Soil nailing, as one of the slope stabilization techniques, has been widely used in upgrading cut slopes [1–4], and is particularly useful for strengthening the existing slopes [5], because of their low construction cost, simple installation procedure, and the ease and speed of construction [6, 7]. The fundamental concept of soil nailing is to reinforce the soil with closely spaced passive inclusions to create a coherent gravity structure, and consequently increase the overall shear strength of the soil in situ, restraining its displacements [8, 9]. In order to assess the stability of a slope reinforced with soil nails, the limit equilibrium method (LEM) [10, 11] is usually adopted. For instance, WEI et al [9] developed the LEM for analyzing the stability of a soil nailed slope based essentially on Spencer’s method; DENG et al [12] and DONG et al [13] analyzed the stability of a soil nailed slope under earthquake using LEM; and TAO et al [14] established the improved general LEM for analyzing the stability of a soil nailed slope. Further, a numerical simulation method [9, 15–17] and failure probability method [2] are also used to study the reinforcement effect of soil nailing in the soil nailed slope. However, in these studies, practical charts for easily analyzing the soil nailed slope stability have not been drawn, and methods to design optimally the parameters of soil nailing for the slope with a certain safety requirement have not been considered.
In this work, a new method for analyzing the stability of a soil nailed slope in limit equilibrium theory framework is established by considering that slope sliding occurs owing to shear failure, which subjects to Mohr–Coulomb (M–C) strength criterion. After comparing the results with the traditional LEM, the feasibility of the current method is verified. In the current method, all the static equilibrium conditions of a sliding body can be satisfied, and hence, the current method can provide a strict limit equilibrium solution. In addition, the factor of safety (FOS) contour curve charts are drawn for analyzing easily the stability of a soil nailed slope, on the basis of the established linear proportional relationship between the spacing of soil nails and slope height, and the length of soil nails and slope height. These charts have been verified with some examples, and they can be also used to design optimally the parameters of soil nailing for the slope to meet a certain safety requirement.
2 LEM for stability of soil nailed slope
2.1 Assumption of stresses on slip surface
In the slope shown in Fig. 1, H is the slope height, and β is the slope angle, m rows of soil nails, numbered by Nj (i=1, 2, …, m), are arranged along the vertical direction with spacing s, while the spacing of soil nails in the horizontal direction is unity. The vertical distance between the position of the first row of soil nails on slope surface and the slope toe is assumed to be s0, and the vertical distance between the position of the m-th row of soil nails on slope surface and the slope top is also assumed to be s0. For the j-th row of soil nails, the design parameters are listed as follows: diameter of anchor bolt dj, diameter of anchoring body Dj, tensile strength of anchor bolt fy, horizontal inclination angle of soil nails δj, length of soil nails Lj, and ultimate frictional resistance of the soil qs. A and B are the lower and upper sliding points of the slip surface, respectively. When an xy-axes coordinate system is established by taking slope toe as the origin point, the y-axis coordinate for the position of the soil nail Nj on slope surface is yNj, and the coordinates for the intersection point of the soil nail Nj and the slip surface are 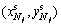 . The equations of the slope surface and slip surface are g(x) and s(x), respectively.
. The equations of the slope surface and slip surface are g(x) and s(x), respectively.

Fig. 1 Calculation mode of soil nailed slope stability analysis:
The parameter m, i.e., the row number of soil nails arranged in the slope along the vertical direction, can be determined from the slope height H and spacing s of soil nails in the vertical direction as
 (1)
(1)
where Int is the integral function.
The vertical distance s0 can be calculated as
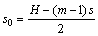 (2)
(2)
In the previous studies, the reinforcement effect of soil nail Nj on the slope has been normally considered as tension force Tj of the soil nail Nj acting on the slip surface to improve the slope stability. In this case, two modes exist for soil nail destruction owing to slope sliding as follows: 1) the soil nail Nj is pulled out from the soil with tension force  where
where  is the length of the soil nail Nj outside the sliding body; 2) the soil nail Nj is pulled off with tension force
is the length of the soil nail Nj outside the sliding body; 2) the soil nail Nj is pulled off with tension force 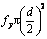 .
.
Therefore, the tension force Tj of the soil nail Nj to maintain the slope stability can be calculated as
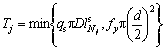 (3)
(3)
In Fig. 1, the vertical slice abcd with the width dx is selected in the sliding body, and the forces acting on the slice under normal conditions are as follows: the weight force wdx, horizontal seismic force kHwdx, vertical seismic force kVwdx, x-axis component of external load on the slope surface qxdx, y-axis component of external load on the slope surface qydx, tension force of soil nail Tj, normal force on the slip surface σdx/cosα, shear force on the slip surface τdx/cosα, and the water force on the slip surface udx/cosα, where kH and kV are the horizontal and vertical seismic coefficient, respectively; σ, τ, and u are the normal, shear and water stresses on the slip surface, respectively; and α is the horizontal inclination angle of the tangent to the slip surface. When the horizontal seismic force points outside of the slope, kH is positive; otherwise, it is negative. When the direction of the vertical seismic force is the same as that of gravity, kV is positive; otherwise, it is negative.
Ignoring the effect of inter-slice forces, the force equilibrium conditions of all forces in slice abcd along the x- and y-axis directions are given as
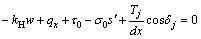 (4a)
(4a)
 (4b)
(4b)
where s′ is the first order of the slip surface equation for x-axis, s′=tanα, and σ0 and τ0 are the normal and shear stresses, respectively, on the slip surface without considering the effect of inter-slice forces.
Solving Eq. (4), σ0 can be obtained as

 (5)
(5)
As σ0 is obtained without considering the effect of inter-slice forces, it has some difference from the actual normal stress. In order to obtain the calculated normal stress σ that is closer to the actual value, the following equation is adopted to amend the initial normal stress σ0 as
 (6)
(6)
where λ1 is the calculation variable, and 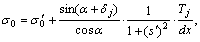

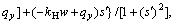 and
and  is the normal stress on the slip surface in the non-reinforced slope without considering the effect of inter-slice forces.
is the normal stress on the slip surface in the non-reinforced slope without considering the effect of inter-slice forces.
Assuming that slope sliding occurs owing to the shear failure, which subjects to the M–C strength criterion, the relationship between the normal stress and shear stress on the slip surface can be obtained as
 (7)
(7)
where Fs is the slope FOS; c is the soil cohesion; and φ is the soil internal friction angle.
Substituting Eq. (6) into Eq. (7), the shear stress on the slip surface is assumed using the following equation as
 (8)
(8)
where λ2 and λ3 are the calculation variables, 
 and
and 
In the sliding body, the force equilibrium conditions of all the forces along x- and y-axis directions and the moment equilibrium condition of all forces around one point (xc, yc) can be obtained as
 (9a)
(9a)
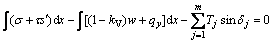 (9b)
(9b)


 (9c)
(9c)
Substituting Eqs. (9a) and (9b) into Eq. (9c), Eq. (9c) can be simplified as


 (10)
(10)
Substituting Eqs. (6) and (8) into Eqs. (9a), (9b) and (10), the linear ternary equations of the variables λ1, λ2, and λ3 are deduced as
 (i=1, 2, 3) (11)
(i=1, 2, 3) (11)
where aij and bi are the calculation parameters, and their formulas are shown in Table 1.
2.2 Calculation of slope FOS
In the M–C strength criterion expressed by Eq. (7), the slope FOS can be defined as the ratio of the failure shear force to the actual shear force acting on the slip surface. Therefore, by summing Eq. (7) over the slip surface, the slope FOS (Fs) is derived as
 (12)
(12)
3 Comparison and analysis with slope examples
Example 1 [13]. In the slope shown in Fig. 2, slope height H=14.18 m, slope angle β=65°, and the soil parameters are as follows: natural unit weight γ=16.00 kN/m3, cohesion c=15.00 kPa, internal friction angle φ=28°, and ultimate frictional resistance of soil qs= 50 kPa. Six rows of soil nails along the vertical direction are arranged in the slope, and the spacing of soil nails in the horizontal direction is unity. The other parameters of soil nailing are shown in Table 2. Given these soil nailing parameters, the results of the slope stability obtained using the Swedish method [18], simplified Bishop method [19], Spencer method [20], Morgenstern–Price (M–P) method [21], and the current method are listed in Table 3.
Table 1 Calculation parameters for soil nailed slope stability analysis
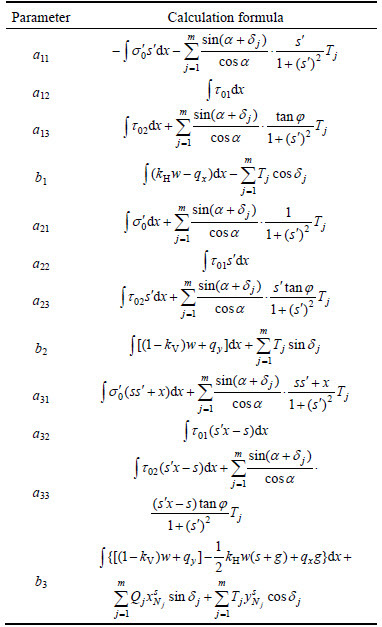
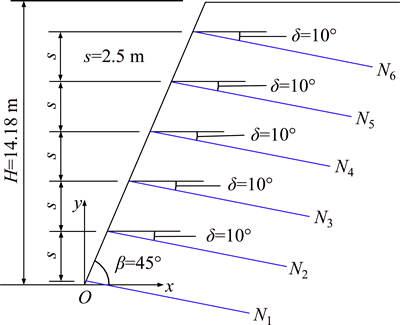
Fig. 2 Slope in Example 1
Table 3 shows that 1) compared with the previous result, the current method has only a little difference, indicating the feasibility of the current method;2) compared with the results of the traditional LEM, the current method yields values larger than those from the Swedish method, and values close to those from simplified method, Spencer method and M–P method, indicating that the current method can provide an strict solution. The reason is that the current method satisfies all the static equilibrium conditions of a sliding body, despite it being established based on the initial normal stress on the slip surface without considering the effect of inter-slice forces.
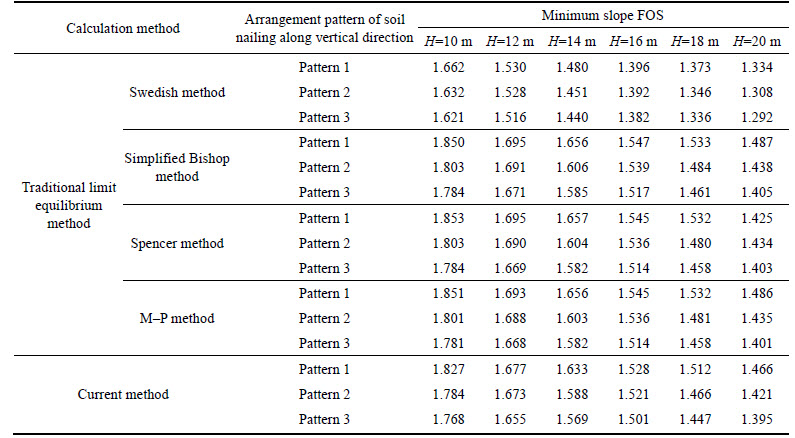
Example 2. In the slope shown in Fig. 3, the slope shape, soil parameters, and design parameters of soil nailing are the same as those in Example 1. Three patterns of arrangement of soil nails along the vertical direction are adopted as follows: 1) Pattern 1: the length of all the soil nails are 0.8H with spacing s in the vertical direction being 0.10H; 2) Pattern 2: the length of all the soil nails are 0.8H with spacing s in the vertical direction being 0.12H; 3) Pattern 3: the length of all the soil nails are 0.8H with spacing s in the vertical direction being 0.14H. In all the three patterns, the spacing of soil nails in the horizontal direction is unity. The vertical distance s0 can be determined using Eq. (2). For slope heights H of 10, 12, 14, 16, 18 and 20 m, respectively, the results obtained using the Swedish method, simplified Bishop method, Spencer method, M–P method, and the current method are listed in Table 4.
Table 2 Design parameters of soil nailing in Example 1
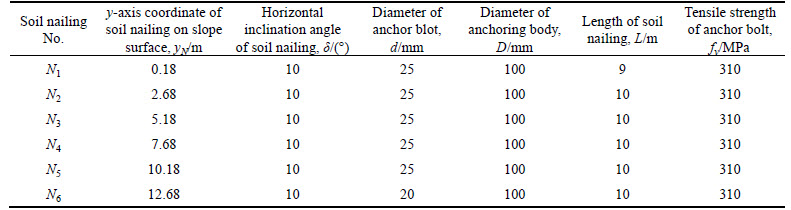
Table 3 Contrast on minimum slope FOS in Example 1

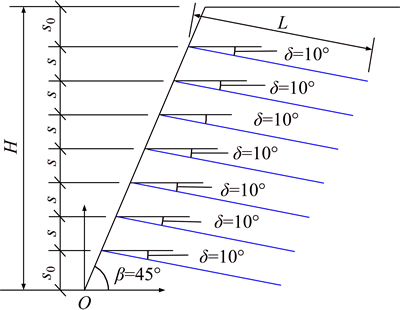
Fig. 3 Slope in Example 2
Table 4 shows that 1) the results from the current method also have a larger value than those from the Swedish method, and have less than 2% difference with respect to the results from the simplified Bishop method, Spencer method, and M–P method; 2) when the spacing s of soil nails in the vertical direction changes from 0.10H to 0.12H with the same length L of soil nails, the slope FOS reduced by less than 5%, indicating that change in the spacing s of soil nails in the vertical direction has little effect on the slope stability; 3) with the linear proportional relationship between the length of soil nails (L) and slope height (H), and the spacing of soil nails and H, despite L and s increase with the increase in H, the calculated slope FOS reduced significantly with their increase, indicating that a high slope has more favorable stability when reinforced with small spacing of soil nails in vertical direction and appropriate length of soil nails.
4 Charts for optimization design of soil nailing parameters and its application
4.1 FOS contour curve for stability analysis of soil nailed slope
As soil nailing is usually adopted to reinforce deep and steep slopes, the slope parameters are assumed as follows: slope height H=10 m, and slope angle β=80°. Let the natural unit weight of soil γ=18 kN/m3, and the design parameters of soil nailing are as follows: diameter of anchor bolt d=18 mm, diameter of anchoring body D= 100 mm, tensile strength of anchor bolt fy=310 MPa, and the horizontal inclination angle of soil nails δ=10°. The spacing of soil nails in the vertical direction is assumed as s=k1H with the spacing in the horizontal direction being unity, and the length of soil nails is assumed as L= k2H, where k1 and k2 are the proportional coefficients. The FOS contour curve charts for the stability analysis of soil nailed slopes is drawn under the following conditions: 1) the values of dimensionless parameter c/(γH) are 0.14, 0.16 and 0.18; 2) the soil internal friction angle φ=15° and 20°, and 3) the soil ultimate friction resistance qs=40 kPa and 60 kPa. These charts are shown in Fig. 4.
Table 4 Contrast on minimum slope FOS in Example 2
4.2 Application and verification of charts
In order to illustrate how the parameters of soil nailing can be designed using Fig. 4 for the soil nailed slope to meet a certain safety requirement, and to verify the feasibility of these obtained design parameters, some examples are listed as follows:
Example 3. Consider a slope having slope height H=10 m, slope angle β=80°, and soil parameters as follows: natural unit weight γ=17.8 kN/m3, cohesion c= 26 kPa, internal friction angle φ=15°, and ultimate friction resistance of soil qs=45 kPa. Design parameters of the soil nailing are as follows: diameter of anchor bolt d=18 mm, diameter of anchoring body D=100 mm, tensile strength of anchor bolt fy=310 MPa, and the horizontal inclination angle of soil nails δ=10°. Let the spacing of soil nails in the vertical direction be s=1 m and the spacing in the horizontal direction be unity. The length L of the soil nails is designed to ensure a slope FOS of 1.4.

Fig. 4 FOS contour curves for soil nailed slope stability analysis:
Table 5 Contrast on minimum slope FOS

Example 4. Consider a slope, where the slope shape, soil parameters, and design parameters of soil nailing are the same as in Example 3. Let the length of soil nails L= 7.1 m, and the spacing of soil nails in the horizontal direction be unity. The spacing s of the soil nails in the vertical direction is designed to ensure a slope FOS of 1.4.
The followings are the known parameters in Examples 3 and 4: H=10 m, β=80°, c/(γH)=0.146, φ=15°, δ=10°, and qs=45 kPa. According to Fig. 4, and using the linear interpolation relationship, the following details can be inferred: 1) In Example 3, the length of soil nails (L) should be equal to 6.976 m to ensure a slope FOS of 1.4; 2) In Example 4, the spacing of soil nails (s) in the vertical direction should be 1.00 m to ensure a slope FOS of 1.4. The results obtained from the Swedish method, simplified Bishop method, Spencer method, M–P method, and the current method are listed in Table 5, using the above design parameters of soil nailing to analyze the stability of soil nailed slopes.
Table 5 shows that 1) compared with the non-reinforced slope, the stability of slope reinforced with soil nails is improved significantly, indicating that the soil nailing plays an effective reinforcement role in strengthening the slope stability; 2) compared with the required slope FOS, the slope FOS calculated using the obtained design parameters of soil nailing has less than 2% difference from it, indicating that using the slope FOS contour curve charts to design the parameters of soil nailing is reliable, and the obtained design parameters of soil nailing can ensure that the soil nailed slope meets the stability requirement.
5 Conclusions
Based on the assumption of stresses on the slip surface, a new method is deduced to analyze the stability of a slope reinforced with soil nails in the limit equilibrium theory framework. After compared the results with the traditional LEM in some examples, the feasibility of the current method is verified. In order to facilitate engineering applications and get the benefit of design optimization for the parameters of soil nailing, the FOS contour curve charts are drawn for the soil nailed slope to analyze the stability, based on the established linear proportional relationship between the length of soil nails and slope height, and the spacing of soil nails and slope height. According to the research conducted for analyzing the stability of soil nailed slope, some conclusions can be drawn as follows:
1) The results obtained from the current method are close to those obtained using the traditional LEM, and the current method can provide an strict solution for the slope FOS, as it satisfies all static equilibrium conditions of a sliding body.
2) For a high slope, the stability of soil nailed slope is more favorable when a small spacing of soil nails in the vertical direction with appropriate length of soil nails is adopted to reinforce the slope.
3) The FOS contour curve charts can be quickly and easily used to analyze the stability of soil nailed slope, and to design optimally the parameters of soil nailing.
References
[1] ZHOU Y D, CHEUK C Y, THAM L G. Numerical modeling of soil nails in loose fill slope under surcharge loading [J]. Computers and Geotechnics, 2009, 36(5): 837–850.
[2] LIU J, SHANG K, WU X. Stability analysis of soil nailing supporting structure based on system failure probability method [C]// International Conference on Sustainable Civil Infrastructure. Yichang, China, 2014: 20–22.
[3] JEON S S. Pull-out tests and slope stability analyses of nailing systems comprising single and multi rebars with grouted cement [J]. Journal of Central South University, 2012, 19(1): 262–272.
[4] SEO H J, LEE I M, LEE S W. Optimization of soil nailing design considering three failure modes [J]. KSCE Journal of Civil Engineering, 2014, 18(2): 488–496.
[5] GARG A, GARG A, TAI K, SREEDEEP S. An integrated SRM-multi-gene genetic programming approach for prediction of factor of safety of 3-D soil nailed slopes [J]. Engineering Applications of Artificial Intelligence, 2014, 30(4): 30–40.
[6] CHEUK C Y, NG C W W, SUN H W. Numerical experiments of soil nails in loose fill slopes subjected to rainfall infiltration effects [J]. Computers and Geotechnics, 2005, 32(4): 290–303.
[7] KIM Y, LEE S, JEONG S, KIM J. The effect of pressure-grouted soil nails on the stability of weathered soil slopes [J]. Computers and Geotechnics, 2013, 49(4): 253–263.
[8] YANG X Q, LIU Z D, HE S X. On design of vertical slopes reinforced by soil-nails [J]. Engineering Mechanics, 1999, 16(5): 125–132. (in Chinese)
[9] WEI W B, CHENG Y M. Soil nailed slope by strength reduction and limit equilibrium methods [J]. Computers and Geotechnics, 2010, 37(5): 602–618.
[10] ZHANG M J, SONG E X, CHEN Z Y. A stability analysis method and its application for soil nailing in excavation [J]. Engineering Mechanics, 1998, 15(3): 36–43. (in Chinese)
[11] HUI C Y, ZHU Y P, YE S H. Stability analysis of composite soil-nailing wall with prestressed anchors [J]. Chinese Journal of Geotechnical Engineering, 2013, 35(s2): 325–329. (in Chinese)
[12] DENG D P, LI L, LUO W. Stability analysis of slope protected by soil nailing under earthquake loads based on pseudo static method [J]. Rock and Soil Mechanics, 2012, 33(6): 1787–1794. (in Chinese)
[13] DONG J H, ZHU Y P. Stability calculation method of a soil side-slope protected by soil nailing under earthquake [J]. Journal of Vibration and Shock, 2009, 28(3): 119–124. (in Chinese)
[14] TAO L N, ZHOU X P, CAI H J. Improved general limit equilibrium method for slope stability analysis [J]. Journal of Civil Architectural and Environmental Engineering, 2014, 36(1): 106–113. (in Chinese)
[15] HALABIAN A M, SHEIKHBAHAEI A M, HASHEMOLHOSSEINI S H. Three dimensional finite difference analysis of soil-nailed walls under static conditions [J]. Geomechanics and Geoengineering, 2012, 7(3): 1–14.
[16] WANG B. Study on Composite soil nailing wall in soft soil area of complex condition with emphasis on analysis by finite element analysis [J]. Applied Mechanics and Materials, 2012, 174–177: 2020–2023.
[17] ZAKI M F M, AHMAD W A A W, AYOB A, YING T K. Analysis of soil nailing under earthquake loading in Malaysia using finite element method [J]. Applied Mechanics and Materials, 2014, 695: 526–529.
[18] FELLENIUS W. Calculation of the stability of earth dams [C]// Proc 2nd Congr Large Dams. Washington, D.C, 1936: 445–462.
[19] BISHOP A W. The use of the slip circle in the stability analysis of earth slopes [J]. Géotechnique, 1955, 5(1): 7–17.
[20] SPENCER E. A method of analysis of the stability of embankments assuming parallel inter-slice forces [J]. Géotechnique, 1967, 17(1): 11–26.
[21] MORGENSTERN N R, PRICE V E. The analysis of the stability of general slip surfaces [J]. Géotechnique, 1965, 15(1): 79–93.
(Edited by FANG Jing-hua)
Cite this article as:
DENG Dong-ping, LI Liang, ZHAO Lian-heng. Limit equilibrium analysis for stability of soil nailed slope and optimum design of soil nailing parameters [J]. Journal of Central South University, 2017, 24(11): 2496–2503.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-017-3662-yFoundation item: Project(2015M580702) supported by the Postdoctoral Science Foundation of China; Project(51608541) supported by the National Natural Science Foundation of China; Project(2014122066) supported by the Guizhou Provincial Department of Transportation Foundation, China
Received date: 2015-09-16; Accepted date: 2016-03-06
Corresponding author: DENG Dong-ping, Assistant Professor, PhD; Tel: +86–13975150476; E-mail: dengdp851112@126.com
Abstract: Reinforcement of slopes using soil nailing can effectively improve slope stability, and it has been widely used in upgrading cut slopes. Based on the assumptions of stresses on the slip surface, a new method for analyzing the stability of a slope reinforced with soil nails was established in the limit equilibrium theory framework, by considering that slope sliding occurs owing to shear failure of the slip surface, which subjects to Mohr–Coulomb (M–C) strength criterion. Meanwhile, in order to easily analyze the stability of a soil nailed slope in actual engineering and facilitate optimum design of parameters for soil nailing, factor of safety (FOS) contour curve charts were drawn on the basis of the established linear proportional relationship between the spacing of soil nails and slope height, and the length of soil nails and slope height. Then, by analyzing and verifying the results obtained from classic examples, some conclusions can be got as follows: 1) The results obtained from the current method are close to those obtained from the traditional limit equilibrium methods, and the current method can provide a strict solution for the slope FOS as it satisfies all the static equilibrium conditions of a sliding body, thus confirming the feasibility of the current method; 2) The slope FOS contour curve charts can be used not only to reliably analyze the stability of a soil nailed slope, but also to design optimally the parameters of soil nailing for the slope with a certain safety requirement.


