改进混合离散粒子群的多种优化策略算法
余伶俐，蔡自兴
(中南大学 信息科学与工程学院，湖南 长沙，410083)
摘 要：
摘 要：针对离散粒子群算法求解旅行商问题，根据组合优化问题和离散量的特点，改进离散粒子群算法更新的运动方程。对离散粒子群算法分别加入逆转变异优化策略、受蚁群启示的变异优化策略和近邻搜索变异优化策略3种优化变异优化策略，使其成为新的混合离散粒子群算法，最后对3种混合离散粒子群算法进行比较，并剖析仿真结果的本质。结果表明：3种优化策略在不同程度上都提高了离散粒子群算法的总体效果和收敛性能，其中，加入逆转变异优化策略的混合粒子群算法实现简单，时间代价较小；加入近邻搜索变异优化策略的混合粒子群算法不论是在最优值或稳定性方面表现最突出。
关键词：
中图分类号：TP301.63 文献标识码：A 文章编号：1672-7207(2009)04-1047-07
Multiple optimization strategies for improving hybrid
discrete particle swarm
YU Ling-li, CAI Zi-xing
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: Updating kenetic equations for discrete particle swarm optimization algorithm were improved to tackle travel salesman problem based on combinatorial optimization problem and discrete variable. Three mutant strategies were designed, which are named reversion mutant strategy, enlighten by ant colony mutant strategy and close neighbor search mutant strategy. Those mutant strategies were added individually and became new hybrid discrete particle swarm optimization algorithms. Those algorithms were compared and the simulation results were analyzed deeply. The result shows that general effects and convergences of discrete particle swarm optimization algorithm increase by those three mutant strategies to different extents. Reversion mutant strategy for discrete particle swarm optimization algorithm achieves simply and costs less time. Close neighbor search mutant strategy for discrete particle swarm optimization algorithm is the most outstanding with the best value and stability.
Key words: discrete particle swarm; mutant strategy; travel salesman problem; ant colony
粒子群优化算法(Particle swarm optimization，PSO)主要模拟鸟集群飞行觅食行为，通过鸟群的集体协作达到寻优目的。在PSO算法中，每个粒子利用自身、历史最优位置和整个粒子群的全局最优解提供的信息，在解空间内不断飞行，实现寻找最优解的目的。粒子群优化算法已成功地应用于求解连续域问题[1]，但对于离散域特别是路由规划和组合优化问题的研究不多[2-4]。Kennedy等[5]提出了一种离散的二进制版本的PSO，定义粒子速度为“粒子位置的改变概率”，结果表明采用经过改造的PSO算法解决了离散函数的优化问题。Clerc[6]针对TSP问题实现了一个具体的DPSO算法，定义速度为交换的列表，并对其他量及运算法则进行了定义，但没有考虑离散量运算规律的不同，与其他算法相比仍有较大的差距。黄岚等[7-9]也利用交换列表的规律强，并定义了不同的离散量运算规则，但由于没有增加局部搜索能力，算法只针对小维数TSP问题进行了仿真。但其算法表现出了很强的进化特征，证明PSO在求解离散优化问题的可行性。离散粒子群算法也可以视为变异和交叉的结合体。同时，也可混入模拟退火的思想，在一定阈值内也可接受变坏解[10]。本文作者主要针对文献[11-12]中算法规则进行细节上的改进，并设计了3种变异优化策略提高离散粒子群算法的综合性能，最后对3种变异优化策略的收敛情况和多样性进行对比与分析。
1 广义粒子群算法
在每次迭代中，所有粒子在N维空间中“移动”以搜索全局最优解。粒子的速度和位置由式(1)和(2)确定。
函数rand()产生0到1之间的随机数。广义粒子群[13]算法步骤可概括为：a. 随机初始化粒子种群，初始化种群中所有粒子的速度和位置(可行解)；b. 根据优化问题目标定义的适应度函数对所有粒子进行评价；c. 根据适应度函数更新种群中每个粒子个体极值；d. 根据适应度函数更新每个粒子所在邻域种群的邻域极值；e. 按照式(1)和(2)进行粒子速度及位置(解)的迭代；f. 重复步骤b~e，直到满足算法的迭代停止条件为止。
2 离散粒子群优化算法
将DPSO运算规则形象地理解为图1所示矢量形式：两位置相减得到1个速度，如图1(a)所示；速度的数乘产生另外1个速度，如图1(b)所示；2个速度相加得到另1个速度，如图1(c)所示；位置与速度相加即位置的移动，得到1个新的位置，如图1(d)所示。设x是N个自然数的1个排列，可直接表示1个可行解或是1种分配方案，把位置x表示成：x={x1, x2,…, xi, …, xN}, 1≤i≤N, 1≤xi≤N。粒子速度可定义为v，是一个N维向量，其作用是改变粒子的位置，可表示为：v={v1, v2, …, v i,…, vN}, 1≤i≤N，1≤vN≤N。
(a) (位置，位置)
(速度); (b) (系数，速度)
(速度);
(c) (速度，速度)
(速度); (d) (位置，速度)
(位置)
图 1 4种运算规则矢量理解图
Fig.1 Four kinds of operational rules
2.1 位置与速度的加法运算
2.2 位置的减法运算
两位置相减所得结果是1个速度，v=x2-x1含义可以用下式来表示[12]：
2.3 速度的数乘运算
定义v=c1vc2(1≤c1, c2≤N)，把维看作是1到N的循环列表，左乘c1表示从c1位置开始，右乘c2表示至c2-1位置结束。在这之间的维的速度取原有值，其余位置值为0。c1和c2为随机产生的数值(c2＞c1)。当c1为速度最后一维数据时，c2= c2-length(v)。这样，就使粒子速度对其各维都较为均衡，使其均衡地向最佳方向飞行，另外，也免去了c参数选取所带来的问题，可以用式(5)表示速度数乘的运算规则。
2.4 速度的加法运算
2个速度相加得到1个新的速度[9]，v=v1+v2，其中vi分量定义为：
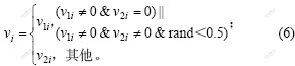
速度加法不再满足交换律。
2.5 改进的粒子运动方程
从社会心理学的观点来看，学习因子C1表示个体学习自身成功行为的能力，称为认知因子，而C2表示学习社会成功行为的能力，称为社会因子。C1 和C2保证搜索到Pgt和Plt为中心的领域所有范围。研究测试了2种极端情况：单社会模型和单认知模型，发现这2个因子对DPSO算法成功搜索到最优值都是必须的。本文作者利用每次迭代过程中每一代的最优值Pct(Current best)，再次影响搜索的效果。C3表示学习本次迭代成功行为的能力，定义为时代因子。实现方法是进一步改进粒子运动方程(如式(9)所示)，重新定义1个当前代粒子最优位置Pct，使得粒子在向当前代的最优值进行逼近同时，也向个体最优和全局最优逼近靠拢。另外，由于DPSO的特殊性，采用分段计算方式会比采用式(7)和(8)的效果好，因为速度对位置上各维数据的作用互相影响。
3 多种优化策略
3.1 逆转变异优化策略
在1~n的城市中随机选取第j1次和第j2次访问城市，在路径C0中第j1次到第j2次访问的城市之间的子路径以反向插入，其余不变，在时的路径为C1。例如：C0=[1, 5, 6, 4, 3, 2]，j1=2，j2=5，则C1=[1, 3, 4, 6, 5, 2]。对于TSP问题，传统的领域产生函数包括互换、逆序和插入等操作，都采用随机方式产生下一个状态，没有考虑到领域知识。另外，逆转变异是插入和互换等盲目随机变异优化策略中最优的一种变异方式，所以，本文选用逆转变异作为此类优化策略的代表，与下列2种优化策略进行比较。
3.2 受蚁群启示的变异优化策略
为了使路径总长度之和(目标函数)达到最小，优先解决薄弱环节，这里采用路径中相邻城市间距离大的2座城市以较大的概率被选取，在其间插入其他城市。采用l(n)数组记录路径C0相邻城市之间的距离，具体数据如下：l(k)=d[c(k), c(k+1)], k=1, 2, …, n-1; l(n)=d[c(n), c(1)]。选取城市i的概率如式(10)所示，按轮转法选取城市i1，其轮转法阈值q0定为0.25；据式(12)，当所产生的随机数小于q0时，选择概率最大值对应的城市，否则按S的规律，即按顺序将概率相加，相加之和的第1次大于此随机数对应的城市号，即为此次轮转应该选择的城市。再选定城市i1后利用点的邻接关系，据文献[14]，距离近的邻接点以较大的概率被选择为下一个访问点。所以，在局部调整时依据此思想。设d(i, j)表示城市i与城市j的距离，离城市i1最远城市距离为dmax=max d(i1, j)，为了排除下一个访问点是其本身，令d(i1, i1)=inf，则下一个访问城市j的概率计算式见式(11)。选择办法仍然使用式(12)的轮转技术，但此时本文中设定轮转法阈值q1=0.5。在原始路径C0中将城市j1安排到城市i1之后，其余不变，此路径为C1。
3.3 近邻搜索变异优化策略
对于TSP问题，最佳路径在很大程度上包括相邻城市间距离最短的边或较短的边，近邻搜索策略利用此规律，计算各城市近邻的排序表，例如KL(i, j)表示离城市i第j近的城市号。在此，本文取j＜3。对每一座城市，若下一个要访问的城市不是最近城市，则以此最近城市作为当前速度，作用到该粒子的位置上；若此时的路径长度减小，则接受此路径。若路径长度没有减小，则再把次近城市当作当前速度，作用到当前粒子的位置上，判断此时路径是否减小，若减小，则接受此解，并将此操作作用到粒子的每一维上。近邻搜索变异优化策略可以使算法在空间搜索和局部开采间取得较好平衡，这种策略也是将启发式算法和仿生算法有机地融合在一起，各尽其责，各取其用。例如，在数据库eil51中的点[26, 8, 48, 27, 6, 18, 4, 47, 12, 17, 37, 44, 42, 19, 40, 41, 13, 24, 43, 7, 23, 14, 25, 51, 46, 32, 11, 38, 49, 9, 34, 30, 10, 39, 33, 45, 15, 5, 2, 20, 29, 21, 50, 16, 1, 22, 35, 36, 3, 28, 31]，经过1次近邻变异后变化成：[26, 8, 48, 27, 6, 18, 4, 47, 12, 17, 37, 44, 42, 19, 40, 41, 13, 25, 14, 24, 43, 7, 23, 51, 46, 32, 11, 38, 49, 9, 50, 34, 30, 10, 39, 33, 45, 15, 5, 2, 20, 29, 21, 16, 1, 22, 35, 36, 3, 28, 31]。
4 混合离散粒子群算法步骤
Step 1：设定粒子数nParticle，规定迭代次数maxIteration,计算距离矩阵dist，随机产生粒子的初始位置和初始速度，即进行初始化。
Step 2：根据距离矩阵dist计算出当前位置的适应值fit-ness，设置当前适应值为个体极值particle_ best，当前极值位置为particle_best_pos；根据各个粒子的个体极值计算全局极值glo bal_best与其极值位置global_best_pos。
Step 3：设置最大迭代次数maxIteration，进入迭代循环，对当前每一个粒子，按照以上4种运算规则和粒子运动方程(9)的顺序进行运算。
Step 4： 根据当前位置curSwarm计算fitness的值。
Step 5：计算各个粒子的多样性；若各粒子多样 性[12]小于0.2，则新位置更新等于随机生成的扰动速度作用于原始位置。
Step 6：各种优化策略。
Step 7：更新各个粒子最优值particle_ best，找出最优值相应位置particle_best_pos；根据各粒子的极值，找出全局极值global_best和全局极值位置global_best_pos。
Step 8：计算每次迭代粒子群的平均多样性[9]。curIteration=curIteration+1。
Step 9：输出结果，画出连接图和平均多样性的曲线，输出全局极值global_best和全局极值位置global_best_pos。
5 仿真实验结果及分析
分别采用模拟退火(SA)、遗传算法(GA)、离散粒子群算法(DPSO)和混合离散粒子群算法(HDPSO)对标准的TSP数据库中的Burma14，Eil51和Berlin52的数据进行仿真实验。其最优值是各种算法测试10次所得路径的最小值，平均值是10次仿真实验的几何平均值，相对误差定义为平均值与最优值之差除以最优值的百分数。本实验设置模拟退火算法参数为起始温度，设置为1 000，终止温度为1，退火速度为0.9；设置遗传算法参数为染色体个数为50，交叉概率为0.2，变异概率为0.3，迭代次数为1 000。在DPSO参数设置中，均选用100个粒子，最大迭代次数为1 000。王翠茹等[9]利用eil51数据算出最优整数路径距离为426，利用本文算法得出的最优值为429.983 3。对本文计算的距离不进行取整，这已是非整数路径的最优值。
如表1所示，在Burma14低维数据中，模拟退火或遗传算法都没有离散粒子群算法的性能稳定，而且最优值的效果也不如由混合离散粒子群算法所得的最优值的效果。但DPSO和加入3种优化策略的DPSO在低维数据中的效果不能区分。在随后的eil51和berlin52中高维数据中各算法效果得到充分体现，加入优化策略的结果不论是在最优解上还是在解的相对误差上均明显优于单纯的DPSO。根据图2~4的仿真结果可知，加了变异优化策略的DPSO在收敛后，粒子仍然保持一定的进化能力，这是加入随机扰动因子产生的效果。所以，随机扰动因子对算法保持多样性避免早熟非常重要。而变异优化策略对提高算法的局部求精能力方面有重要意义。
表1 多种策略的混合离散粒子群算法的对比
Table 1 Comparison results of multiple strategies for hybrid discrete particle swarm algorithm
(a) 近邻搜索变异优化策略DPSO最优值收敛；
(b) 近邻搜索变异策略DPSO平均多样性；
(c) 3种策略的最佳周游路径
图2 Burma14问题上的仿真数据
Fig.2 Simulation data for Burma14
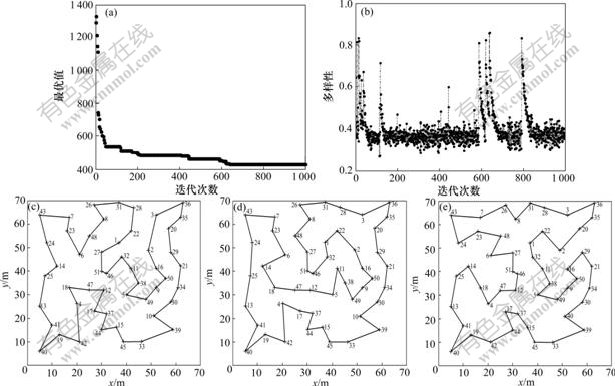
(a) 近邻搜索变异优化策略DPSO最优值收敛；(b) 近邻搜索变异优化策略DPSO平均多样性；(c) 逆转变异优化策略DPSO最佳路径；(d)受蚁群启示的变异优化策略DPSO最佳周游路径；(e) 近邻搜索变异优化策略DPSO最佳周游路径
图3 在51个城市eil51问题上的仿真数据
Fig.3 51 cities simulation data for eil51
(a) 近邻搜索变异优化策略DPSO最优值收敛；(b) 近邻搜索变异优化策略DPSO平均多样性；(c) 逆转变异优化策略DPSO最佳周游路径；(d) 受蚁群启示的变异优化策略DPSO最佳路径；(e) 近邻搜索变异优化策略DPSO最佳周游路径
图4 在52个城市Berlin52问题上的仿真数据
Fig.4 52 cities simulation data for Berlin52
综上所述，近邻搜索变异优化策略综合性能优于其它2种变异优化策略的综合性能，表现在近邻搜索变异优化策略的最优解效果最佳，并且相对误差较小，算法较稳定。本质原因在于近邻搜索变异优化策略能进一步搜索每个粒子当前的位置领域，提高了局部搜索能力，使得算法在求精能力上增强。而蚁群启示变异优化策略稳定性最弱，这与蚁群算法机制有关。若在选择上恰好选中亟待变异优化的点，则算法效果可以提高；若赌轮法选中的点变异优化对总体影响不大，则效果不理想。这与蚁群算法很大程度上依赖于初始值原理类似。赌轮法虽然是一种有启发信息的变异优化策略，但并没有较大程度地改进算法的局部搜索能力。另外，在本实验中，受蚁群启示的变异优化策略的幅度设置不大，只是针对2个被选城市进行优化变异，没有作用于每一维的粒子位置，所以，变异力度不够。若作用于每维粒子的位置，则算法所需时间相当大。同时，受蚁群启示的变异优化策略最佳周游路径交叉概率比另2种变异优化策略概率大，建议在最佳路径后进行去交叉操作。逆转变异优化策略是盲目变异优化策略中局部搜索能力较强的一种，所以，其算法综合效果可以接受，且简单易行。
6 结 论
a. 目前，DPSO的研究多采用交换子和交换序列的概念，作者认为其具有非惟一性，会降低算法的搜索效率，所以需采用有效的规则运算方式，使可行解的编码方式易与实际应用相联系。
b. 在实现算法过程中，考虑到DPSO算法更新位置方式的特殊性，文中的粒子位置采用的是单链表的概念形式，比采用置换方式要好。
参考文献：
[1] 李 婷, 赖旭芝, 吴 敏. 基于双种群粒子群优化新算法的最优潮流求解[J]. 中南大学学报: 自然科学版, 2007, 38(1): 133-137.
LI Ting, LAI Xu-zhi, WU Min. A novel two-swarm based particle swarm optimization algorithm for optimal power flow problem[J]. Journal of Central South University: Science and Technology, 2007, 38(1): 133-137.
[2] Jarboui B, Damak N, Siarry P, et al. A combinatorial particle swarm optimization for solving multi-mode resource-constrained project scheduling problems[J]. Applied Mathematics and Computation, 2008, 195(1): 299-308.
[3] Qi H, Ruan L M, Shi M. Application of multi-phase particle swarm optimization technique to inverse radiation problem[J]. Journal of Quantitative Spectroscopy & Radiative Transfer, 2008, 109(3): 476-493.
[4] Pan Q K, Tasgetiren M F, Liang Y C. A discrete particle swarm optimization algorithm for the no-wait flow shop scheduling problem[J]. Computers & Operations Research, 2008, 35(9): 2807-2839.
[5] Kennedy J, Eberhart R C. A discrete binary version of the particle swarm algorithm[C]//Proceedings of the World Multi conference on Systemic, Cybernetics and Informatics. Piscataway: IEEE Service Center, 1997: 4104-4109.
[6] Clerc M, Kennedy J. The particle swarm-explosion, stability and convergence in a multi-dimensional complex space[J]. IEEE Trans on Evolutionary Computation, 2002, 6(1): 58-73
[7] 黄 岚, 王康平, 周春光, 等. 粒子群优化算法求解旅行商问题[J]. 吉林大学学报: 理学版, 2003, 41(4): 477-480.
HUANG Lan, WANG Kang-ping, ZHOU Chun-guang. Particle swarm optimization for traveling salesman problems[J]. Acta Scientiarium Naturalium Universitatis Jilinensis, 2003, 41(4): 477-480.
[8] 肖健梅, 李军军, 王锡淮. 改进微粒群优化算法求解旅行商问题[J]. 计算机工程与应用, 2004, 35: 50-52.
XIAO Jian-mei, LI Jun-jun, WANG Xi-huai. A modified particle swarm optimization for traveling salesman problems[J]. Computer Engineering and Applications, 2004, 35: 50-52.
[9] 王翠茹, 张江维, 王 玥, 等. 改进粒子群优化算法求解旅行商问题[J]. 华北电力大学学报, 2005, 32(6): 57-59.
WANG Cui-ru, ZHANG Jiang-wei, WANG Yue, et al. Modified particle swarm optimization algorithm for traveling salesman problem[J]. Journal of North China Electric Power University, 2005, 32(6): 57-59.
[10] 高 尚, 韩 斌, 吴小俊, 等. 求解旅行商问题的混合粒子群优化算法[J]. 控制与决策, 2004, 19(11): 1286-1289.
GAO Shang, HAN Bin, WU Xiao-jun, et al. Solving traveling salesman problem by hybrid particle swarm optimization algorithm[J]. Control and Decision, 2004, 19(11): 1286-1289.
[11] 钟一文, 才荣英. 求解二次分配问题的离散粒子群优化算法[J]. 自动化学报, 2007, 33(8): 871-874.
ZHONG Yi-wen, CAI Rong-ying. Discrete particle swarm optimization algorithm for QAP[J]. Acta Automatica Sinica, 2007, 33(8): 871-874.
[12] 钟一文, 宁正元, 蔡荣英. 一种改进的离散粒子群优化算法 [J]. 小型微型计算机系统, 2006, 27(10): 1893-1896.
ZHONG Yi-wen, NING Zheng-yuan, CAI Rong-ying. An improved discrete particle swarm optimization algorithm[J]. Mini-micro Systems, 2006, 27(10): 1893-1896.
[13] 高海兵, 周 驰, 高 亮. 广义粒子群优化模型[J]. 计算机学报, 2005, 28(12): 1980-1987.
GAO Hai-bing, ZHOU Chi, GAO Liang. General particle swarm optimization model[J]. Chinese Journal of Computers, 2005, 28(12): 1980-1987.
[14] 吕 强, 汤贤铭, 愈金寿. 基于信息素机制的离散粒子群算法及其应用[J]. 系统仿真学报, 2008, 20(2): 395-398.
L? Qiang, TANG Xian-ming, YU Jing-shou. Discrete particle swarm optimization algorithm and its application based on pheromone mechanism[J].Journal of System Simulation, 2008, 20(2): 395-398.
收稿日期：2008-09-05；修回日期：2008-11-25
基金项目：NSFC重大研究计划项目(90820302)；国家博士点基金资助项目(200805330005)
通信作者：蔡自兴(1938-)，男，福建莆田人，教授，博士生导师，从事人工智能和机器人研究；电话：0731-88877355；E-mail: zxcai@mail.csu.edu.cn
