FEM analysis for hot rolling process of AM60 alloy
DING Han-lin(丁汉林), KANAMORI Nao, HONMA Tomoyuki, KAMADO Shigeharu, KOJIMA Yo
Department of Mechanical Engineering, Nagaoka University of Technology, 1603-1, Kamitomioka,
Nagaoka, Niigata 940-2188, Japan
Received 12 June 2008; accepted 5 September 2008
Abstract:
The rolling of AM60 sheets for 50% reduction was analyzed with DEFORM to investigate the hot deformation process. The simulated results show that the sheet velocities at the entrance (21 mm/s) and at the exit (37 mm/s) are less and larger than roll velocity, respectively. From the entrance to the neutral point, the velocity at the sheet surface is greater than that at the middle point of sheet in thickness, while that from the neutral point to the exit shows the opposite pattern. The effective strain of the sheet increases from the entrance to the exit due to the continuous reduction in thickness. In addition, the effective strain at the sheet surface reaches to 1.0 and is larger than that of 0.8 at the middle point of sheet. The difference of effective strain in thickness direction has a much stronger effect on the recrystallized fraction than on the recrystallized grain size. The minimum temperature of 347
Keywords: hot rolling; finite element method; effective strain; AM60 alloy
1 Introduction
With increasing applications of magnesium alloys to automotive industry, much higher demands, such as good castability, high ductility, and heat resistance, have been required for die-casting alloys. Among the commercial cast Mg alloys, AM60 alloy is recommended for applications where greater ductility and toughness are required[1]. The reported results[2-4] showed that the deformation at warm or high temperature was a possible method to obtain fine-grained structures in Mg alloys. Recently, grain refinement has been widely utilized for Mg alloys to obtain improved properties at ambient temperature[5-9]. A recent study found that the recrystallized grains of AM60 alloy could be reduced to 1 μm by large strain rolling, which produced one pass of 80% thickness reduction and resulted in higher strain rate[10]. Almost all the results were obtained from the observation of the rolled sheet after deformation. It is difficult to study the deformation behavior like the change of temperature and strain during the hot rolling by experimental methods.
In the present study, the rigid-thermoviscoplastic FEM was applied to investigate the hot rolling process through the rolling of AM60 sheets under one pass of 50% reduction. The distributions of temperature and strain in deformation zone were studied, as well as their effect on the recrystallized microstructure. In order to obtain the flow stress curves of the sheet material used in the database of DEFORM, the tensile tests of AM60 alloy were carried out at high temperatures corresponding to the stress conditions similar to those during rolling.
2 Experimental
The investigated AM60 (Mg-6.0%Al-0.3%Mn) alloy was produced by unidirectional casting. The tensile test samples with 4 mm in diameter and 20 mm in gauge length were machined from the material homogenized at 424 ℃ for 24 h. The tensile tests were carried out at 300 ℃, 350 ℃ and 400 ℃ with initial strain rates of 10-1 s-1, 10-2 s-1, 10-3 s-1 and 10-4 s-1, respectively. The AM60 casting block with 60 mm in width, 30 mm in thickness and 300 mm in length was used for rolling experiment. The sheet was rolled to 15 mm, which corresponds to 50% reduction in thickness. Prior to hot rolling, the sheet was heated to 380 ℃ and then held for 5 min in an electric furnace with Ar protection.
The rolls with 320 mm in diameter were heated to 300 ℃ and the velocity of rolls was set as 2 mm/min (about 2 r/min). The schematic drawing of deformation zone during rolling is presented in Fig.1.
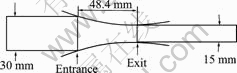
Fig.1 Schematic drawing of deformation zone during hot rolling for 50% reduction in thickness
3 Constitutive analysis of tensile tests
Constitutive equations, used to predict the relationships between the strain rate, strain, stress and temperature, have been applied frequently in the investigations of hot deformation. There are two favorite equations: one is the power law (
) which is not satisfied at high stress and the other is exponential law (
) which is not satisfied at high tempera- tures. Due to the limitation of the power law and exponential law, the hyperbolic-sine constitutive law is introduced [11-12]:
(1)
where α(=β/n′) is an additional adjustable constant; A′, A″, A, n′ and β are material constants, 
is the strain rate; σ is the stress during the deformation process; Q is the deformation activate energy; R(=8.314 J·mol-1·K-1) is the gas constant; T is the absolute temperature and Z is the Zener-Hollomon parameter.
In this study, the ultimate tensile strengths of AM60 alloy in investigated conditions shown in Fig.2 are used to discuss the relationship between the strain rates and the stresses. The experimental data are fitted to the power
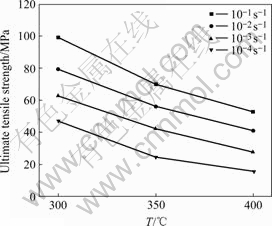
Fig.2 Ultimate tensile strength of AM60 alloy tested under different conditions
law and exponential law respectively and then the average value of n′ of 7.2 and β of 0.157 can be obtained. Then the value of α is equal to 0.022 MPa-1, which is used in the following studies.
The activation energy related to deformation process can generally be derived from an Arrhenius plot and can also be calculated according to Eqn.(1):
(2)
The relationship between ln() and ln[sinh (ασp)] and the dependence of ln[sinh (ασp)] on (1 000/T) are shown in Fig.3. It is noted that good linear relationships can be obtained using the experimental data. By calculating the values of slopes, a mean value of Q of 185 kJ/mol is deduced from Eqn.(2). Thus, the relationship between ln Z and ln[sinh (ασp)] can be plotted in Fig.4 with α=0.022 MPa-1 and Q=185 kJ/mol. It is an evidently linear relationship and the relationship can be described as follows:
(3)
Combining Eqns.(1) and (3), the relationship between strain rate and stress can be written as:
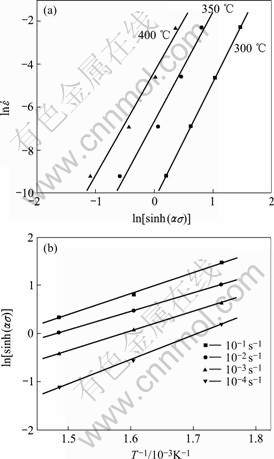
Fig.3 Constitutive analysis of tensile test of AM60 alloy according to Eqn.(1)
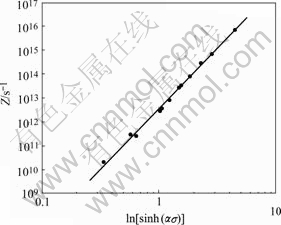
Fig.4 Relationship between Z parameter and stress of AM60 alloy
(4)
where A is equal to 3.45×1012 and n is 5.07. Then Eqn.(4) is used in DEFORM to predict and calculate the flow stress of AM60 alloy during hot rolling.
4 DEFORM simulation and analysis
4.1 DEFORM simulation
The commercial software DEFORM-3D system was used in the present study. The size of AM60 sheet used for DEFORM analysis and the rolling conditions were the same as those in hot rolling experiments. Considering the strong symmetry of the rolling sheet, the simulation was carried out using only 1/4 volume (1/2 thickness and 1/2 width) of entire sheet. The flow stress—strain curves of AM60 alloy used in DEFORM was derived from tensile tests at high temperatures, just as shown in Eqn.4. The material of rolls is AISI-D2 alloy. In this simulation, the rolls and sheet were set to be rigid and plastic, respectively. The heat transfer among the rolls, sheet and environment was considered. The other physical parameters used in DEFORM are list in Table 1[13].
4.2 DEFORM results
The rolling force loaded on the sheet surface is predicted from the simulation, as shown in Fig.5. Since the present simulation is carried out on only 1/2 thickness of entire sheet, the actual rolling force should be twice as much as the simulated value. Therefore, the simulated rolling force varies from 279 to 293 kN, which is similar with the experimental value (281 kN) obtained from the rolling machine. In general, it is well-known that it is difficult to predict the value of rolling force during the experiment because it depends not only on sheet size but also on rolling conditions, such as the sheet width, reduced thickness and rolling temperature. However, the present analysis shows that it is an effective method to precisely predict the rolling force by means of DEFORM simulation, which is favorable to the design of practical experiments.
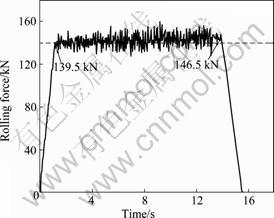
Fig.5 Rolling force loaded on sheet with 50% reduction in thickness
It can be seen from Fig.1 that the reduced thickness of the sheet located in the deformation zone is different at a given time. That is to say, the deformation of the sheet in the deformation zone is inhomogeneous, which can be characterized by sheet velocity, effective strain and so on. Due to the strong symmetry of the rolling sheet, only the surface and the middle of the sheet are illustrated in the following analysis. The sheet velocity in the deformation zone is depicted in Fig.6. In the simulation, the roll speed is set as a constant of 2 m/min (about 33 mm/s). However, the sheet velocity is different and increases from the entrance to the exit. The sheet velocities near the entrance and the exit are 21 mm/s and 36 mm/s, respectively. The sheet near the entrance is moving slower than that near the roll (designed as backward slip), while that near the exit is moving faster than roll (designed as forward slip). The neutral point is located at about 34 mm from the entrance of the deformation zone. On the other hand, the velocity at the surface of sheet from the entrance to neutral point is larger than that of the middle of sheet, whereas that from the neutral point to the exit shows the opposite pattern.
Table 1 Physical parameters used in DEFORM analysis
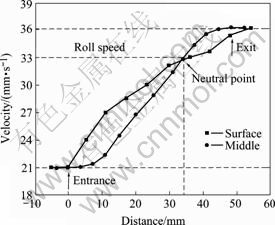
Fig.6 Velocity of surface and middle of sheet located in deformation zone
Fig.7 shows the variations of the effective strain at the surface and middle of the sheet. The effective strains increase gradually from entrance to exit and those at the surface and middle of the sheet reach to 1.0 and 0.8, respectively. This indicates that the distribution of effective strain is not uniform, which is the main reason for an inhomogeneous microstructure in a rolling sheet. The temperature distribution of deformation zone during the rolling is shown in Fig.8. Prior to the hot rolling, the temperatures of the sheet and the roll are set as 380 ℃ and 300 ℃, respectively. Due to the heat transfer between lower-temperature roller and environment, the sheet temperature tends to decrease. At the same time, the sheet temperature will increase because of the energy conversion during plastic deformation as well as the friction between the roller and sheet. It is just because the competition between them results in the inhomogeneous distribution of temperature in the rolled sheet. As shown in Fig.8, the minimum temperature in A region contacted with the roll is 347 ℃, while the maximum temperature in H region in the middle of the sheet is 388 ℃. That is to say, there is a slight temperature gradient between surface and middle of the sheet after hot rolling.
Fig.7 Variations of effective strain at surface and middle of sheet
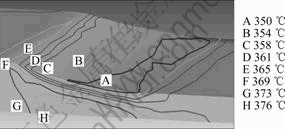
Fig.8 Temperature distribution of rolled sheet
Recrystallization is expected to occur during hot rolling of magnesium alloys because it is a thermally activated process[14]. Fig.9 shows the optical micrographs of AM60 alloy rolled with a reduction of 50%. At the middle of the rolled sheet, partially recrystallized microstructure can be found with an average recrystallized grain size of 11.4 μm, whereas the examined area at the surface of specimen is fully recrystallized with a fine grain size of 11.8 μm. Obviously, dynamic recrystallization during hot rolling gives rise to the grain refinement of AM60 ally. But the microstructural observation shows that the deformation microstructure is inhomogeneous at different region of the rolled sheet.
In the present simulation, it is worthwhile to note that inhomogeneous distributions of effective strain and temperature exist not only in the rolling direction of deformation zone, but also in the thickness direction from surface to middle of the rolled sheet. An inhomogeneous strain distribution most likely results in the absence of dynamic recrystallization in the middle of rolled sheet. In general, the progressively accumulated strain during plastic deformation provides necessary energy for the nucleation of recrystallized grain[15]. It can be seen from Fig.7 that the strain at the exit is much larger than that at the entrance. That is to say, there are a large number of strains accumulate in the sheet during hot rolling, which is responsible for the occurrence of dynamic recrystallization. On the other hand, the strain at the surface is larger than that in the middle of the sheet. In Fig.9, an approximate size of recrystallized grains can be found at the surface and middle of rolled sheet. However, the recrystallization at the surface is completed, whereas the fraction of dynamic recrystallization is about 70% in the middle of the sheet. In other words, this fact means that the strength of effective strain has a much stronger effect on the recrystallized fraction than on the recrystallized grain size.
Fig.9 Microstructures of AM60 alloy sheet rolled with reduction of 50%: (a) At surface; (b) In middle
5 Conclusions
1) The hyperbolic-sine constitutive law (
A? [sinh (ασ)]nexp(-Q/RT)) is used to describe the flow curves used in DEFORM. The values of the parameters determined by the tensile test are A=3.45×1012, a=0.022 MPa-1, n=5.07, Q=185 kJ/mol and R=8.314 J·mol-1·K-1.
2) The sheet velocity at the entrance (21 mm/s) is less than roll velocity and that at the exit (37 mm/s) is larger than roll velocity. From the entrance to the neutral point, the velocity at the sheet surface is greater than that at the middle point of sheet in thickness, while that from the neutral point to the exit shows the opposite pattern.
3) The effective strain of the sheet increases from the entrance to the exit due to the increasing reduction in thickness. In addition, the effective strain reaches to 1.0 at the sheet surface and is larger than that of 0.8 at the middle point of sheet, which is responsible for the formation of inhomogeneous microstructure.
4) Deformation and friction result in an increase in sheet temperature, while heat transfer between roller and environment results in a decrease in sheet temperature. The minimum temperature of 347 ℃ is obtained at the surface contacted directly with roller and the maximum temperature of 388 ℃ at the middle point of sheet.
5) From comparison of the optical microstructures of rolled sheet, it is found that effective strain has a much stronger effect on the recrystallized fraction than on the recrystallized grain size.
References
[1] MORDIKE B L, EBERT T. Magnesium: Properties—applications— potential [J]. Mater Sci Eng A, 2001, 302(1): 37-45.
[2] GUO Q, YAN H G, CHEN Z H, ZHANG H. Grain refinement in as-cast AZ80 Mg alloy under large strain deformation [J]. Mater Character, 2007, 58: 162-167.
[3] KIM W J, PARK J D, KIM W Y. Effect of differential speed rolling on microstructure and mechanical properties of an AZ91 magnesium alloy [J]. J Alloys Comp, 2008, 460(1/2): 289-293.
[4] YANG X Y, MIURA H, SAKAI T. Recrystallization behaviour of fine-grained magnesium alloy after hot deformation [J]. Trans Nonferrous Met Soc China, 2007, 17(6): 1139-1142.
[5] DALLA TORRE F H, H?NZI A C, UGGOWITZER P J. Microstructure and mechanical properties of microalloyed and equal channel angular extruded Mg alloys [J]. Scripta Mater, 2008, 59(2): 207-210.
[6] DING H L, LIU L F, KAMADO S, DING W J, KOJIMA Y. Study of the microstructure, texture and tensile properties of as-extruded AZ91 magnesium alloy [J]. J Alloys Comp, 2008, 456(1/2): 400- 406.
[7] KANG S H, LEE Y S, LEE J H. Effect of grain refinement of magnesium alloy AZ31 by severe plastic deformation on material characteristics [J]. J Mater Proc Tech, 2008, 201(1/3): 436-440.
[8] KAI M, HORITA Z, LANGDON T G. Developing grain refinement and superplasticity in a magnesium alloy processed by high-pressure torsion [J]. Mater Sci Eng A, 2008, 488(1/2): 117-124.
[9] KIM W J, YOO S J, KIM H K. Superplastic microforming of Mg-9Al-1Zn alloy with ultrafine-grained microstructure [J]. Scripta Mater, 2008, 59(6): 599-602.
[10] P?REZ-PRADO M T, DEL VALLE J A, CONTRERAS J M, RUANO O A. Microstructural evolution during large strain hot rolling of an AM60 Mg alloy [J]. Scripta Mater, 2004, 50(5): 661- 665.
[11] MWEMBELA A, KONOPLEVA E V, MCQUEEN H J. Microstructural development in Mg alloy AZ31 during hot working [J]. Scripta Mater, 1997, 37(11): 1789-1795.
[12] MCQUEEN H J, RYAN N D. Constitutive analysis in hot working [J]. Mater Sci Eng A, 2002, 322(1/2): 43-63.
[13] MICHAEL M A, Hugh B. ASM speciality handbook—Magnesium and magnesium alloys [M]. Meterals Park (OH): ASM International, 1999.
[14] HUMPHREYS F J, HATHERLY M. Recrystallization and related annealing phenomena [M]. 2nd ed. Oxford: Elsevier, 2004.
[15] JIN Q Q, SHIM S Y, LIM S G. Correlation of microstructural evolution and formation of basal texture in a coarse grained Mg-Al alloy during hot rolling [J]. Scripta Mater, 2006, 55(9): 843-846.
Corresponding author: DING Han-lin, Tel: +81-258-47-1611(7304); E-mail: hanlinding@yahoo.com
