基于改进EM算法的混凝土泵车数据治理-有色金属在线

远程监控中存在数据缺失的问题，提出一种基于随机期望最大化算法的缺失数据治理算法，通过将马尔科夫链蒙特卡洛方法(MCMC)与随机变量相结合改进期望最大化(EM)算法。首先，在期望步中，在MCMC矩阵中采样生成缺失值，并将该值代入进行随机近似模拟以更新估计值。然后，在最大化步中，通过反复迭代得到最大化估计值作为重构值来填充缺失数据。最后，以混凝土泵车实际运行数据对本文提出的算法、均值填充法和EM算法的缺失数据填充效果进行比较。研究结果表明：所提算法有效地解决了EM算法依赖初始值设定的问题，提高了数据填充的准确率。

关键词：

数据缺失；随机过程；改进EM算法；数据治理；

中图分类号：TP311 文献标志码：A OSID：

文章编号：1672-7207（2021）02-0443-07

An improved expectation maximization algorithm for missing data management of concrete pump truck

DENG　Ziwei¹, TANG　Zhaohui¹, ZHU　Hongqiu¹, ZHAO　Yuqian^{1, 2}

(1. School of Automation, Central South University, Changsha 410083, China;

2. Hunan Engineering Research Center of High Strength Fastener Intelligent Manufacturing,Changde 415701, China)

Abstract: To solve the recovery problem of data missing in remote monitoring of concrete pump truck, an improved EM missing data filling model based on the stochastic process was proposed, which combines the Markov Chain Monte Carlo(MCMC) and random variables to improve the EM algorithm. Firstly, in the expectation steps, the missing values were sampled in the MCMC matrix, and were applied in the stochastic approximation to update the estimation. Secondly, the maximization steps in EM algorithm were applied iteratively to find the most possible estimated value as the reconstruction value. Finally, compared with the mean filling method and EM algorithm, the proposed method was verified by using the remote monitoring data of pump truck data. The results show that the improved EM algorithm effectively reduces the dependence on the initial setting value and improves the accuracy of data filling.

Key words: data missing; stochastic process; improved EM algorithm; data recovery algorithm

近年来，随着物联网等信息技术的发展，在工业过程中积累了大量的数据，充分利用这些工业大数据对推动生产过程智能化具有重要意义^[1^-6]。然而，由于实际应用中采集的大数据中不可避免地存在缺失值，严重影响了大数据分析、建模效果，因此，对缺失数据进行治理对于准确地建立数据模型尤为必要。以混凝土泵车为例，其运行过程中采集的数据由于受数据采集过程中传感器异常以及数据传输过程中数据丢失等影响，造成数据不完备问题，影响了远程监控、生产管理分析以及基于数据的故障诊断等应用效果，并且混凝土泵车的数据通常缺失比例偏大，进一步给大数据的应用带来了极大困难，因此，研究缺失数据的填充方法尤为必要^[7]。缺失数据恢复是数据分析研究的一个热点问题，也是基于数据的分析处理方法的基础。目前，人们对有关缺失值处理方法进行了大量研究，针对不同的应用场景，提出了一系列解决方法^[8^-9]，如位数/众数/均值插补法、基于分层模型的缺失数据插补方法^[10]、贝叶斯网络和时间序列法等^[11]。杨巧巧等^[12]将SNM算法用于相似重复记录数据的清洗。蒋辉等^[11]在基于朴素贝叶斯方法训练初始数据集的基础上，对每个可能缺失的变量构建相应的单变量预测估计模型来填充缺失值。BATISTA等^[13]将KNN方法运用于丢失数据的填充。李正欣等^[14]利用最小二乘支持向量机分别进行多变量填补和单变量填补，并根据填补结果的差异度，提出一种组合阈值填补方法。吕政等^[15]针对钢铁企业副产煤气的发生、消耗流量数据出现的缺失情况，通过分析相似工况下能源流量数据的相关特性，提出一种基于最大方差权信息系数的冶金企业副产煤气系统流量数据填补方法。邹薇等^[16]利用朴素贝叶斯模型改进了EM缺失数据填充算法。本文作者针对混凝土泵车的数据特点，在分析EM算法的基础上研究缺失数据的填充算法，提出一种基于随机过程改进的EM缺失数据填充算法，使其更有效地填充修复缺失数据。最后，将所提出算法应用于混凝土泵车实际运行数据填充，并与均值填充法和基于原始EM算法的缺失数据填充进行比较，验证本文所提算法的有效性。

1 EM数据填充算法及其改进

EM算法是一种应用较广泛的缺失数据填充算法，通过迭代寻找数据分布参数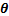和缺失值z的可能最大似然性。但当缺失的信息量很大或完全数据对数似然的估计本身比较复杂时，EM算法的收敛速度会很慢。同时，EM算法十分依赖于待估参数给定的初始值，若初始值设定不好，可能导致算法不收敛，因此，在数据相互依赖度较强、不完整度较高、初始值设定不准等情况下，该方法效率会大大降低。为了解决上述算法收敛及准确性的问题，本文引入随机过程近似的办法来改进EM算法，以提高数据填补的准确性。

1.1　传统EM算法

在数理统计中，最大似然估计(the maximum likelihood estimation，MLE)具有合理性与易操作性等特点，常被用于根据样本数据估计总体分布的某个或某几个关键参数，从而达到通过样本来分析总体数据的目的^[17]。MLE是一种非常有效的参数估计方法，但当数据中有缺失值时，求取MLE十分困难。EM算法可以将估计过程分为2步：第一步求期望，以便将多余的部分去除；第二步求似然函数的极大值。

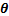
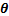
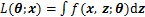
假设观察到的有缺失值的泵车数据x服从某种概率分布，z表示缺失数据，因此，在EM算法中，(x，z)被认为是完全数据。函数f(x；z；)表示取决于参数的完整数据的联合分布。构造新的密度函数，就可以定义新的似然函数：

(1)

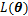
式(1)是不完整数据的似然函数，目标是找到合适的使得边际似然函数取到最大值。EM算法分2步即E步和M步，具体步骤如下。

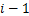
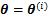
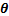
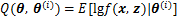
1) 期望步(E步)。在已有数据x和第步即当前估计值的条件下，求基于完全数据的对数似然函数L(x；z；)期望(对与z有关的部分积分)：

(2)

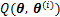
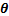
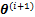
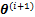
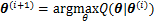
2) 最大化步(M步)。求关于的最大值，即找使得

(3)

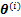
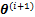
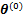
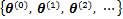
这样就完成了1次由到的迭代。再返回E步，直到满足停止条件为止。在一定条件下，给定初始值，EM算法将产生一系列最终收敛于的估计值序列。

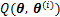
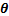
EM算法的核心就是利用缺失值(引入的潜变量z来最大化随机效应函数，避开了棘手的最大化似然函数L(；x)的问题。

1.2　随机过程算法

引入随机过程的原理来改进EM算法。首先模拟生成一系列样本即缺失值。模拟生成数据有很多种方法，但为了更好地从数据分布中生成样本，选用马尔科夫链蒙特卡络方法(即MCMC算法，Markov Chain Monte Carlo)。其基本思想是：构造一条Markov链，使其平稳分布为待估参数的后验分布，通过这条马尔科夫链产生后验分布的样本，并对基于马尔科夫链达到平稳分布时的样本(有效样本)进行蒙特卡洛积分。

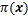
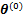
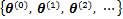
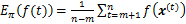
MCMC算法的步骤为：首先构造1条Markov链并且其收敛到平稳分布。从样本空间中的某一点出发，用上述Markov链进行抽样模拟产生点序列，也就是。最后，进行蒙特卡洛积分。任意函数f(x)的期望估计为

(4)

其中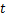：为迭代次数。

MCMC主要包括Metropolis-Hastings算法^[18]和Gibbs^[19]采样2种方法，它们是作为一种从高维复杂概率分布中近似采样的方法，常用于求解数学和物理问题的数值解，如概率统计上的期望、微分方程的解等。本文采用Metropolis-Hastings算法进行求解。

1.3　随机过程改进EM算法

EM算法在运用于实际情况时，所得结果容易受初始值设定的影响。为了避免这一问题，将随机过程引入EM算法，提出改进的EM算法，使用MCMC代替地估计缺失值。利用该方法的优势提高缺失值估计精度。

所提算法仍可分为期望(E)步和最大化(M)步。而本算法的期望步可以进一步细分为模拟步与随机近似步2步。

1) 期望步(E步)分为模拟步和随机近似步。

模拟步：从MCMC算法转移矩阵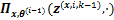中抽样到模拟数据。

随机近似步：

(5)

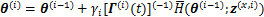
2) 最大化步(M步)：

(6)

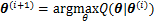
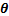
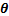
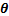
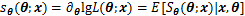
一阶导与二阶偏导数可由完整数据的似然函数l_c(；x；z)得出。对L(；x)取对数并对求一阶偏导数即得分方程：

(7)

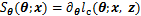
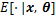
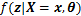
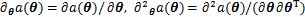
其中：；表示缺失数据条件分布的期望。求导记为

(8)

则方程的二阶偏导为

(9)

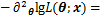
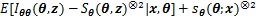
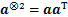
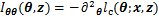
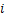
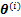
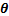
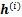
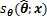
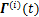
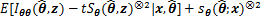
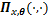
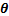
其中：；，表示完整数据的信息矩阵。在第次迭代时，表示当前对的估计；表示当前；表示当前对的估计。假设是给定x和情况下生成的z转移概率矩阵，具体求解步骤如下。

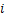
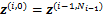
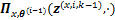
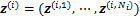
1) 在第次迭代时，设。转移概率矩阵中生成。

2) 更新估计值如下：；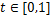

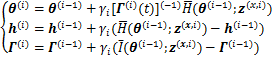
(10)

其中：

(11)

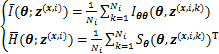
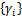
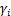
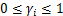
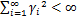
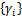
式(10)和(11)中，常数序列满足：对所有有，且。马尔科夫改进EM算法的一个特点就是其应用了常数序列来模拟步骤2中可能存在的噪声。可见，参数的更新求解方式得到改进。传统EM算法主要是使用似然函数完成期望最大化迭代更新，而所提方法主要借助MCMC利用求导和转移概率矩阵进行估计。本文提出的改进算法流程如下。

2 实验验证及分析

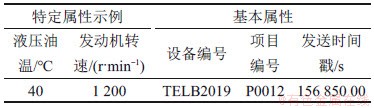
这里使用的实验数据均来自于实际生产场景中混凝土泵车传回来的数据。每个信号量文件内都包含各自特定属性以及3个基本属性即发送时间戳、设备编号和项目编号。具体信号的属性示例数据如表1所示。

表1　不同信号量文件字段及示例数据

Table 1　Different semaphore file fields and sample data

为了验证所提方法的有效性，将数据分为训练集、测试集和验证集，通过循环迭代优化模型^[20]。实时采集泵车运行数据，人为地按一定比例随机模拟数据异常或数据丢失，训练集、测试集和验证集比例分别为10%，15%和20%。然后，将模型填补的重构缺失值与原始数据进行比较，进而对算法的填充效果进行评价。

液压油温和发动机转速分别如图1和图2所示。

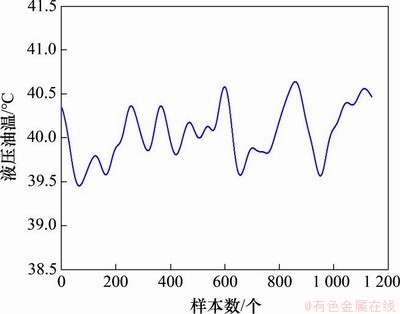
FX_GRP_ID80003F0B

图1　设备液压油温变化曲线

Fig. 1　Temperature change curve of equipment hydraulic oil

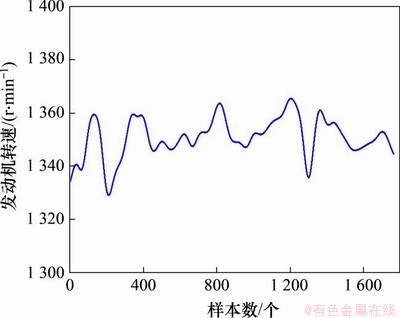
FX_GRP_ID80004056

图2　发动机转速变化曲线

Fig. 2　Engine rotating speed change curve

其次，分别对3台设备的液压油温和发动机转速进行描述统计分析。本文选用平均绝对离差M_ad、标准平均离差平方R_mse和标准方差S_d这3个统计量作为评价标准。具体定义如下。

1) 平均绝对离差M_ad：

(12)

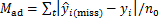
其中：为第个缺失值的估计值；为其对应的真值；n₀为缺失值总数。

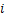
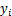
2) 标准平均离差平方和R_mse：

(13)

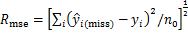
3) 标准差S_d：

(14)

其中：为样本的平均值。

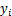
采用均值填充算法、EM填充算法和本文提出的算法对液压油温和发动机转速的缺失数据进行填充补全后，得到的结果如表2所示。从表2可以看出：在不同缺失率下，本文提出的改进EM算法填充的标准偏差最接近完整数据集的标准偏差，EM算法的标准偏差次之，均值填充算法的标准偏差最大。因此，本文提出的算法具有较高的准确度和稳定性。

表2　3种填充方法的比较结果(标准差)

Table 2　Comparison results of three filling methods(S_d)

此外，还计算出不同填充方法的M_ad与R_mse并进行对比，如表3所示。从表3可以看出：本文提出的改进EM算法的M_ad与R_mse在3种数据缺失率下均比均值填充和EM算法的低，但随着缺失率增大，填充准确率略有减小。为了更加直观地比较3种方法在不同缺失率下的效果，图3和图4所示分别为液压油温填补结果M_ad和R_mse的对比。显然，本文所提方法的M_ad和R_mse均为最小，证明了本文所提方法的有效性。

表3　液压油温填补结果比较

Table 3　Comparison results of hydraulic oil temperature filling

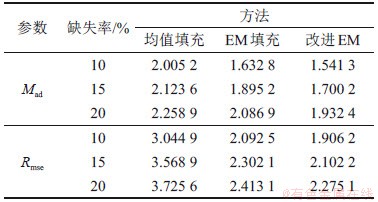
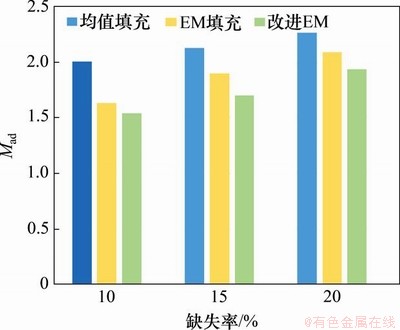
FX_GRP_ID800055DF

图3　液压油温填补M_ad比较

Fig. 3　Comparison results of M_ad of hydraulic oil temperature filling

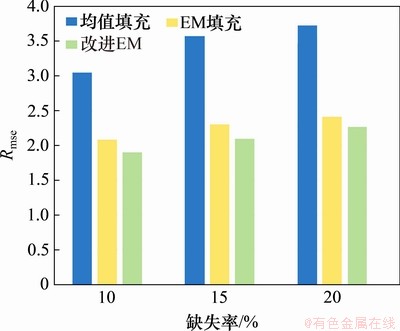
FX_GRP_ID8000575C

图4　液压油温填补R_mse比较

Fig. 4　Comparison results of R_mse of hydraulic oil temperature filling

3 结论

1) 在混凝土泵车远程监控数据在数据采集以及传输过程中，会不可避免地存在数据异常和数据丢失现象。针对该问题，将MCMC方法和EM算法结合，提出一种基于随机过程的EM缺失数据填充算法，通过引入随机过程近似的办法来改进EM算法的填充效果。首先，在期望步中，MCMC矩阵中采样生成缺失值。然后，将该值代入进行随机近似模拟以更新估计值，并在最大化步中通过反复迭代得到最大化估计值作为重构值来填充缺失数据。最后，采用实际的远程监控数据对所提方法进行验证分析，并与均值填充方法和EM填充方法进行比较。

2) 改进的EM算法的M_ad与R_mse在3种数据缺失率下均比均值填充和EM算法的低，但是随着缺失率增大，填充准确率略下降，表明该改进填充方法可以较好地提高EM算法的性能，有效解决了EM算法依赖初始值设定的问题，提高了填充数据的准确率。

参考文献：

[1] 何文韬, 邵诚. 工业大数据分析技术的发展及其面临的挑战[J]. 信息与控制, 2018, 47(4): 398-410.

HE Wentao, SHAO Cheng. The development and challenges of industrial big data analysis technology[J]. Information and Control, 2018, 47(4): 398-410.

[2] 刘薇, 陈英, 高佳风. 大数据分析及其对企业管理的挑战和机遇[J]. 吉林建筑大学学报, 2015, 32(3): 89-92.

LIU Wei, CHEN Ying, GAO Jiafeng. Large data analysis and the challenge and opportunity to enterprise management[J]. Journal of Jilin Jianzhu University, 2015, 32(3): 89-92.

[3] 梁志宇, 王宏志, 李建中, 等. 制造业中的大数据分析技术应用研究综述[J]. 机械, 2018, 45(6): 1-13.

LIANG Zhiyu, WANG Hongzhi, LI Jianzhong, et al. A review on the application of big data analysis in manufacture industry[J]. Machinery, 2018, 45(6): 1-13.

[4] MORENO J, GOMEZ J, SERRANO M A, et al. Application of security reference architecture to big data ecosystems in an industrial scenario[J]. Software:Practice and Experience, 2020, 50(8): 1520-1538.

[5] QIN S J. Process data analytics in the era of big data[J]. AIChE Journal, 2014, 9(60): 3092-3100.

[6] LEI Y, LI N, GONTARZ S, et al. A model-based method for remaining useful life prediction of machinery[J]. IEEE Transactions on Reliability, 2016, 65(3): 1314-1326.

[7] 邓建新, 单路宝, 贺德强, 等. 缺失数据的处理方法及其发展趋势[J]. 统计与决策, 2019, 35(23): 28-34.

DENG Jianxin, SHAN Lubao, HE Deqiang, et al. Processing method of missing data and its developing tendency[J]. Statistics and Decision, 2019, 35(23): 28-34.

[8] 陈海洋, 刘喜庆, 环晓敏. 一步预测的SVDDBN缺失数据插补算法[J]. 计算机工程与应用, 2020, 56(7): 81-87.

CHEN Haiyang, LIU Xiqing, HUAN Xiaoming. One-step prediction SVDDBN missing data interpolation algorithm[J]. Computer Engineering and Application, 2020, 56(7): 81-87.

[9] 高峥, 徐震. 基于多元回归KNN的油田缺失数据填充方法[J]. 信息技术, 2020, 44(4): 79-83.

GAO Zheng, XU Zhen. Filling method of missing data in oilfield based on multiple regression KNN[J]. Information Technology, 2020, 44(4): 79-83.

[10] 于力超, 金勇进. 基于分层模型的缺失数据插补方法研究[J]. 统计研究, 2018, 35(11): 95-106.

YU Lichao, JIN Yongjin. Research on comparison of missing data imputation methods based on multilevel models[J]. Statistical Research, 2018, 35(11): 95-106.

[11] 蒋辉, 马超群, 许旭庆, 等. 仿EM的多变量缺失数据填补算法及其在信用评估中的应用[J]. 中国管理科学, 2019, 27(3): 11-19.

JIANG Hui, MA Chaoqun, XU Xuqing, et al. An EM-similar imputation algorithm for multivariable data missing and its application in credit scoring[J]. Chinese Journal of Management Science, 2019, 27(3): 11-19.

[12] 杨巧巧, 郭振波, 王开西. 基于聚类分组和属性综合权值的SNM改进算法[J]. 工业控制计算机, 2017, 30(9): 27-31.

YANG Qiaoqiao, GUO Zhenbo, WANG Kaixi. Improved SNM algorithm based on clustering-based grouping and attribute weights[J]. Industrial Control Computer, 2017, 30(9): 27-31.

[13] BATISTA G E A P A, MONARD M C. An analysis of four missing data treatment methods for supervised learning[J]. Applied Artificial Intelligence, 2003, 17(5/6): 519-533.

[14] 李正欣, 张凤鸣, 王瑛, 等. 多元时间序列缺失数据填补方法[J]. 系统工程与电子技术, 2018, 40(1): 225-230.

LI Zhengxin, ZHANG Fengming, WANG Ying, et al. Method of missing data imputation for multivariate time series[J]. Systems Engineering and Electronics, 2018, 40(1): 225-230.

[15] 吕政, 赵珺, 刘颖, 等. 基于最大方差权信息系数的煤气数据填补[J]. 控制理论与应用, 2015, 32(5): 646-654.

LU Zheng, ZHAO Jun, LIU Ying, et al. Missing data imputation based on maximal variance weight information coefficient for gas flow in steel industry[J]. Control Theory & Applications, 2015, 32(5): 646-654.

[16] 邹薇, 王会进. 基于朴素贝叶斯的EM缺失数据填充算法[J]. 微型机与应用, 2011, 30(16): 75-77, 81.

ZOU Wei, WANG Huijin. EM algorithm to implement missing values based on Naive Bayesian[J]. Microcomputer & Its Application, 2011, 30(16): 75-77, 81.

[17] 康宏亮. 随机删失数据下极大似然估计量的性质[J]. 兰州文理学院学报(自然科学版), 2019, 33(2): 1-7.

KANG Hongliang. Properties of maximum likelihood estimator under random censored data[J]. Journal of Lanzhou University of Arts and Science(Science and Technology), 2019, 33(2): 1-7.

[18] 鲁帆, 严登华. 基于广义极值分布和Metropolis-Hastings抽样算法的贝叶斯MCMC洪水频率分析方法[J]. 水利学报, 2013, 44(8): 942-949.

LU Fan, YAN Denghua. Bayesian MCMC flood frequency analysis based on generalized extreme value distribution and Metropolis-Hastings algorithm[J]. Journal of Hydraulic Engineering, 2013, 44(8): 942-949.

[19] 乔世君, 张世英. 用Gibbs抽样算法计算定数截尾时Weibull分布的贝叶斯估计[J]. 数理统计与管理, 2000, 19(2): 35-40.

QIAO Shijun, ZHANG Shiying. Bayesian analysis of weibull distribution by using Gibbs sampler[J]. Application of Statistics and Management, 2000, 19(2): 35-40.

[20] 陈先来, 杨路明. 基于均矢量相似性的机器学习样本集划分[J]. 中南大学学报(自然科学版), 2009, 40(6): 1636-1641.

CHEN Xianlai, YANG Luming. Partitioning machine learning sample set using similarity to mean vector[J]. Journal of Central South University(Science and Technology), 2009, 40(6): 1636-1641.

(编辑陈灿华)

收稿日期： 2020 -06 -20; 修回日期： 2020 -09 -08

基金项目(Foundation item)：国家工信部重点资助项目(TC19083WB) (Project(TC19083WB) supported by Key Program of the National Ministry of Industry and Information)

通信作者：朱红求，博士，教授，从事复杂工业过程监测、优化与控制等研究；E-mail:hqcsu@csu.edu.cn

引用格式：邓子畏, 唐朝晖, 朱红求, 等. 基于改进EM算法的混凝土泵车数据治理[J]. 中南大学学报(自然科学版), 2021, 52(2): 443-449.

Citation: DENG Ziwei, TANG Zhaohui, ZHU Hongqiu, et al. An improved expectation maximization algorithm for missing data management of concrete pump truck[J]. Journal of Central South University(Science and Technology), 2021, 52(2): 443-449.

摘要：针对混凝土泵车远程监控中存在数据缺失的问题，提出一种基于随机期望最大化算法的缺失数据治理算法，通过将马尔科夫链蒙特卡洛方法(MCMC)与随机变量相结合改进期望最大化(EM)算法。首先，在期望步中，在MCMC矩阵中采样生成缺失值，并将该值代入进行随机近似模拟以更新估计值。然后，在最大化步中，通过反复迭代得到最大化估计值作为重构值来填充缺失数据。最后，以混凝土泵车实际运行数据对本文提出的算法、均值填充法和EM算法的缺失数据填充效果进行比较。研究结果表明：所提算法有效地解决了EM算法依赖初始值设定的问题，提高了数据填充的准确率。