
J. Cent. South Univ. (2021) 28: 247-263
DOI: https://doi.org/10.1007/s11771-021-4600-6
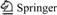
Support pressure assessment for deep buried railway tunnels using BQ-index
WANG Ming-nian(王明年)1, 2, WANG Zhi-long(王志龙)1, 2, TONG Jian-jun(童建军)1, 2,
ZHANG Xiao(张霄)1, 2, DONG Yu-cang(董宇苍)1, 2, LIU Da-gang(刘大刚)1, 2
1. Key Laboratory of Transportation Tunnel Engineering of Ministry of Education,
Southwest Jiaotong University, Chengdu 610031, China;
2. School of Civil Engineering, Southwest Jiaotong University, Chengdu 610031, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
Estimation of support pressure is extremely important to the support system design and the construction safety of tunnels. At present, there are many methods for the estimation of support pressure based on different rock mass classification systems, such as Q system, GSI system and RMR system. However, various rock mass classification systems are based on different tunnel geologic conditions in various regions. Therefore, each rock mass classification system has a certain regionality. In China, the BQ-Inex (BQ system) has been widely used in the field of rock engineering ever since its development. Unfortunately, there is still no estimation method of support pressure with BQ-index as parameters. Based on the field test data from 54 tunnels in China, a new empirical method considering BQ-Inex , tunnel span and rock weight is proposed to estimate the support pressure using multiple nonlinear regression analysis methods. And then the significance and necessity of support pressure estimation method for the safety of tunnel construction in China is explained through the comparison and analysis with the existing internationally widely used support pressure estimation methods of RMR system, Q system and GSI system. Finally, the empirical method of estimating the support pressure based on BQ-index was applied to designing the support system in the China’s high-speed railway tunnel—Zhengwan high-speed railway and the rationality of this method has been verified through the data of field test.
Key words:
Cite this article as:
WANG Ming-nian, WANG Zhi-long, TONG Jian-jun, ZHANG Xiao, DONG Yu-cang, LIU Da-gang. Support pressure assessment for deep buried railway tunnels using BQ-index [J]. Journal of Central South University, 2021, 28(1): 247-263.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4600-61 Introduction
The reliable prediction of tunnel support pressure is important for tunnel construction. Reasonable calculation method of support pressure and accurate calculation value are of great significance for the safety and economy of tunnel construction. Starting with Terzaghi’s rock load estimation method [1], several empirical approaches using rock classification systems have been developed to estimate the support pressure in tunnels [2-20]. Most of these divide the tunnel conditions into several clear different classes and correlate these classes with stable support systems. Certainly, there are many analytical approaches based on elasto-plastic closed-from solutions [21-32] and other methods based on numerical studies [33] and physical modelling [34] for support pressure estimation in literature. The above empirical estimation methods based on rock mass classification have provided important guidance to the preliminary design of tunnel support systems.
Different rock mass classification methods adopt different support pressure estimation methods [35] (see Table 1). Among them, the RMR system [5, 36, 37], Q system [6, 22], and GSI system [38-44] are the most widely used in the field of rock engineering.
In China, many classification systems have been put forward for different rock engineering projects. For example, the HC system [45-47] is used in hydropower stations and the M-IRMR system [48] is used in undersea mining deposits. The rock mass basic quality (BQ) system [49] is the only national guideline for rock mass classifications in China. This system has been widespread used in various rock engineering projects in China [50-55]. However, the support pressure estimation method based on BQ-index has not been proposed.
In this paper a new assessment method for tunnel support pressure is proposed by considering the rock mass classification index (BQ-index). Field tunnel support pressure data for a total of 54 typical tunnels and 205 support pressure test-sections in China is collected. Then the relationships between the support pressure and BQ-index, tunnel span are analyzed using the multivariate linear regression analysis method. The differences of the calculation methods for the support pressure of each rock mass classification systems (BQ, Q, RMR and GSI) are analyzed according to the relationship between the three types of rock mass classification indexes. Finally, the proposed empirical calculation method is applied to the support pressure calculation in Zhengwan high-speed railway, Hubei province, China.
Table 1 Summary of various empirical methods for support pressure estimation
2 BQ system
Since the rock mass classification method of BQ system (Table 2) has been described in detail [49, 56, 57], only a brief introduction is provided here. Similar with other international classification systems (i.e. RMR, Q and GSI systems), BQ is a quantitative classification scheme. The BQ value is determined by two parameters: rock strength (Rc) and rock mass integrity (Kv), as shown in Eq. (1):
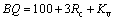 (1)
(1)
where rock strength (Rc) is determined by the uniaxial compressive strength of saturation rock (σi, MPa), the Kv value can be calculated from the elastic longitudinal wave velocity of rock mass (Vpm, km/s), and the elastic longitudinal wave velocity of rock (Vpr, km/s) as:
 (2)
(2)
Considering the negative impact of the existence geological environment conditions and the excavation impact, the BQ value needs to be adjusted as follows: three coefficients, groundwater condition K1, orientation of weakness zone related to the excavation K2 and in-situ stress condition K3, are considered to revise the value BQ as [49]:
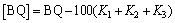 (3)
(3)
Table 2 Basic quality classification of rock mass

3 Support pressure assessment method based on BQ system
3.1 Sample data
Through in-situ measurement and literature research, field pressure data from 54 tunnels and 205 pressure test-sections in China were obtained (as shown in Figure 1).
The samples were further classified according to the different rock mass class and tunnel span, as shown in Figures 1 and 2. It can be seen that most of the samples are classified into classes IV and V, with a proportion of 45% and 40%, respectively. The data with tunnel span of 14.12-15.2 m take up 78% of the whole.

Figure 1 Classification of rock mass class
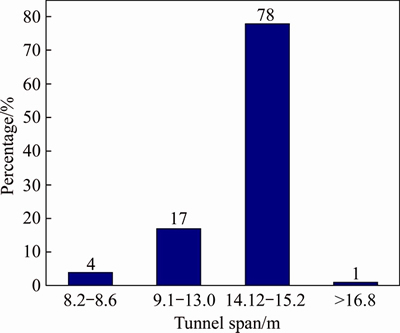
Figure 2 Classification of tunnel span
3.2 Parametric analysis for support pressure
According to the analysis of sample data, the factors affecting the support pressure in the statistical data mainly included the rock mass class and tunnel span. Therefore, the relationships between support pressure and rock mass class and tunnel were analyzed through mathematical statistics method.
3.2.1 Analysis method
The measured radial support pressure is decomposed into vertical and horizontal uniform pressure according to the principle of area equivalence, as shown in Figure 3, where σ1, σ2, σ3, σ4 and σ5 are measured radial support pressure values, θ is the angle between the radial pressure direction and vertical, h is the tunnel height, B is the tunnel span, and λ is the lateral pressure coefficient.
Thus, the vertical support pressure can be obtained as:
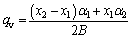 (4)
(4)
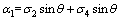 (5)
(5)
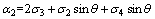 (6)
(6)
The horizontal support pressure can be obtained as:
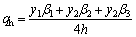 (7)
(7)
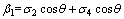 (8)
(8)
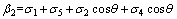 (9)
(9)
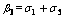 (10)
(10)
The lateral pressure coefficient can be obtained as:
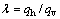 (11)
(11)
3.2.2 Analysis of rock mass class
In order to eliminate the influence of tunnel span on support pressure, only the arithmetic mean value of support pressure was studied. It can be seen that the support pressure increases exponentially with the rock mass class, with a correlation coefficient of 0.93, as shown in Figure 4.
3.2.3 Analysis of tunnel span
In order to eliminate the influence of rock mass class on support pressure, the average support pressure was analyzed. The tunnel span (B) in the sample was divided into 4 sections, namely 8.2- 8.4 m, 9.1-13.0 m, 14.2-15.2 m and over 16.8 m. The concept of influence coefficient of tunnel span(w=0.2+0.1B) was proposed in order to improve the fitting accuracy. The support pressure increased with influence coefficient of tunnel span in two ways, with correlation coefficient of 0.936 for linear function and 0.92 for power function, as shown in Figures 5 and 6.
The variation of support pressure with rock mass class and tunnel span has been summarized in Table 3.
3.3 Analysis of lateral pressure coefficient
In order to get the horizontal support pressure, the lateral pressure coefficient was analyzed. As shown in Table 4, the lateral pressure coefficient basically follows the Gaussian distribution.
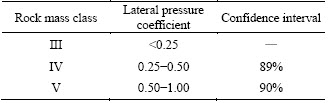
According to the confidence interval, as shown in Figures 7 and 8, the range of lateral pressure coefficient under each rock mass class can be determined (see Table 5).
3.4 Calculation equation of support pressure
Based on the parametric analysis, two equations are proposed to calculate the support pressure, as shown in Table 6. The equation that produces the highest correlation coefficient is selected.
Thus, the equation for vertical support pressure is:
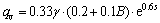 (12)
(12)
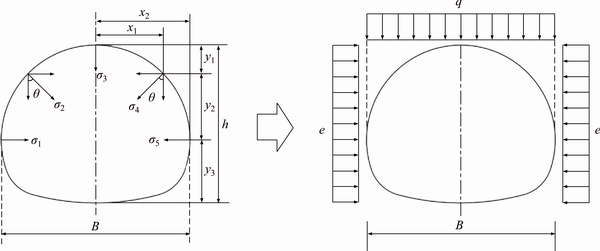
Figure 3 Support pressure test point arrangement and pressure distribution mode
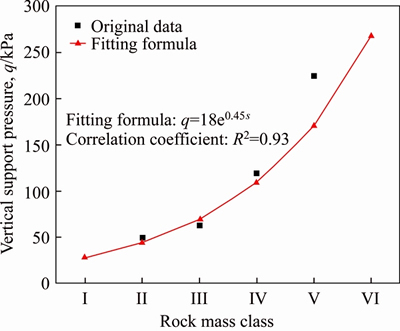
Figure 4 Variation curve of vertical support pressure
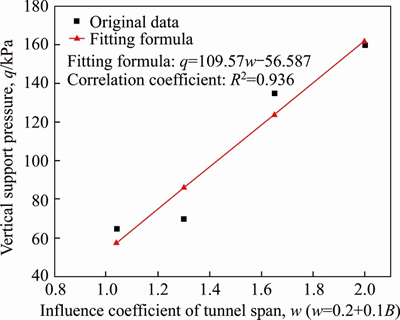
Figure 5 Variation curve of vertical surrounding rock (linear function)
The equation for horizontal support pressure is:
qh=λqv (13)
As can be seen from Table 2, a rock mass class will recommend a range of BQ value. If the rock mass class is used to evaluate the support pressure, the support pressure will increase discontinuously with the rock mass class, as shown in Figure 9. This phenomenon of discontinuous increase of support pressure with rock mass class may cause certain errors in practical engineering applications. In order to avoid this phenomenon, an equation for calculating the support pressure with the BQ value as an independent variable is established according to the relationship between the rock mass class and the BQ value.
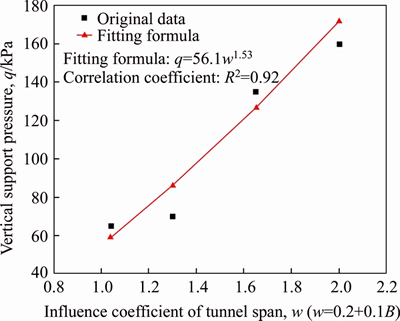
Figure 6 Variation curve of vertical surrounding rock (power function)
Therefore, the transformation function between the rock mass class and the BQ value will be established through the corresponding relationship between the rock mass class and the BQ value. The same rock mass class is divided into n equal parts, and the corresponding BQ value is also divided into n equal parts. The transformation relationship between rock mass class and BQ value is obtained through linear regression analysis. The transformation equation is as follows:
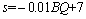 (14)
(14)
Equation (14) is introduced into Eq. (12) to obtain Eq. (15) to calculate the vertical support pressure.
Table 3 Variation of support pressure with various factors

Table 4 Gaussian distribution function table

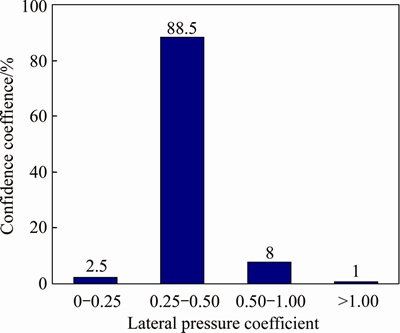
Figure 7 Distribution of lateral pressure coefficient (IV)
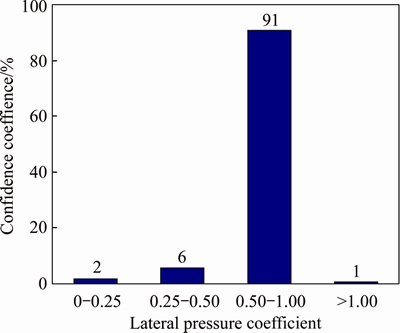
Figure 8 Distribution of lateral pressure coefficient (V)
Table 5 Lateral load coefficient table
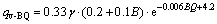 (15)
(15)
Similarly, the lateral pressure coefficient of the same class is divided into n parts, and the transformation relationship between BQ value and lateral pressure is established. The transformation equation is as follows:
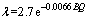 (16)
(16)
Equation (16) is introduced into Eq. (13) to obtain Eq. (17) to calculate the horizontal support pressure.
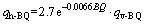 (17)
(17)
The variation of support pressure with BQ value and tunnel span are shown in Figure 10.
4 Comparative analysis of support pressure assessment methods
Different rock mass classification methods have different support pressure estimation methods. Among them, the RMR system, the Q system and GSI system are the most representative classification methods of rock mass in the world. So, a comparison of these three rock mass classification systems is performed.
4.1 Q system
The Q system was established in 1974 by BARTON et al [6] in Norway after analyzing 212 tunnel engineering samples. It mainly uses six parameters to determine the Q value of the rock mass quality index, which are rock quality designation (RQD), joint set number (Jn), joint roughness number (Jr), joint alteration number(Ja), joint water reduction factor (Jw), and stress reduction factor (SRF). The equation to determine Q is:
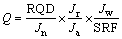 (18)
(18)
And the support pressure assessment method is proposed using the Q system parameters, as shown in Eqs. (19) and (20).
Table 6 Equation of vertical support pressure

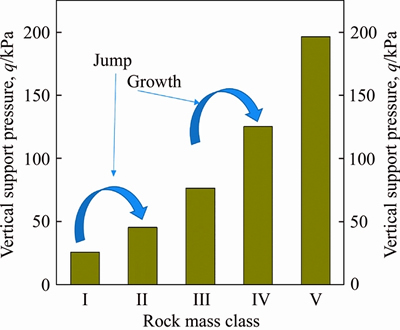
Figure 9 Variation of support pressure with rock mass class

Figure 10 Variation of support pressure
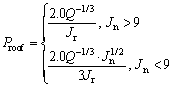 (19)
(19)
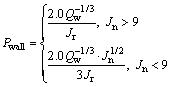 (20)
(20)
When Q>10, Qw=5Q; when 0.1
4.2 RMR system
The RMR system was proposed in 1973 by BIENIAWSKI [36] and has been revised 4 times. Currently, the 1989 version of the RMR system is widely used in engineering practice. The RMR system uses six indicators to evaluate the stability of rock mass, namely, strength of intact rock material (R1), rock quality designation RQD (%), rating (R2), spacing of discontinuities rating (R3), condition of discontinuities (R4), groundwater (R5) and effect of discontinuity strike and orientations in tunneling (R6). The sum of the scores is the RMR value, as shown in Eq. (21).
 (21)
(21)
The support pressure can be determined from the RMR system as proposed in Ref. [58], as shown in Eq. (22). GOEL et al [19] have proposed a correlation for estimating the support pressure using BIENIAWSKI’s RMR, as shown in Eq. (23). The advantage of this correlation is that it can be applied for both non-squeezing and squeezing ground conditions without an advance knowledge of the ground conditions. The correlation is as follows:
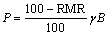 (22)
(22)
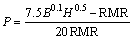 (23)
(23)
where H is the depth of the tunnel (m); B is the span of the tunnel (m).
4.3 GSI system
HOEK [39] proposed the geological strength index (GSI) to obtain reliable input data. In the last decade, the GSI-index has been further developed and modified, particularly for poor and heterogeneous rock masses in tunnels, slopes and foundations. After that the empirical equations were developed to estimate support pressure based on the GSI-index by OSGOUI et al [31] as
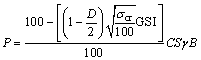 ,
,
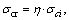
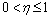 (24)
(24)
where GSI is the geological strength index, which defines the quality of the rock mass; D is the disturbance factor representing different excavation method (drill and blast or TBM); σcr is the uniaxial compressive strength of rock material in the broken zone around the tunnel; B is the span of the tunnel; γ is the unit weight of overburden; C is the correction factor for horizontal to vertical field stress ratio (k); S is the correction factor for squeezing and non squeezing ground condition; and η is the post-peak strength reduction factor characterizing the brittleness of the rock material.
4.4 Comparative discussion
There is no uniform rock mass classification method in the world. And different rock mass classification methods take different classification indicators and classification standards. Statistical analyses have found that there are significant correlations between different rock mass classification systems [59-61]. Therefore, the support pressure assessment methods of each classification system are established based on the relationship between the BQ-index, Q-index, RMR-index and GSI-index. The main ideas are shown in Figure 11.
The empirical relationships of RMR and BQ [59], Q and RMR [60], GSI and RMR [61] are shown as follows:
RMR=(BQ-80.79)/6.09 (25)
Q=exp((RMR-44)/9) (26)
GSI=RMR-5 (27)
In order to compare and analyze the support pressure of each rock mass classification system, equations for calculating the indexes value under the RMR, Q and GSI systems are established according to the conversion relationship between the classification indexes and BQ value, as shown in Eqs. (28) and (29).
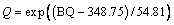 (28)
(28)
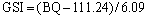 (29)
(29)
Combining Eqs. (19), (23) and (24), the support pressure calculations of each classification system with BQ value are deduced and expressed in Eqs. (30)-(32). And the support pressure value of each system is expressed in Figure 11.
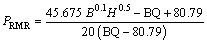 (30)
(30)
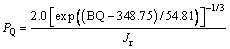 (31)
(31)
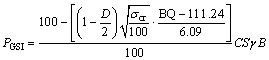 (32)
(32)
In Figure 12, it can be seen that the support pressure of each method decreases continuously with the increase of BQ values (Q, RMR, GSI), but the variation law is different. When the BQ value is 360 (Q is above 1.23), the support pressure of Q system is close to 0. The support pressure value increases with the increase of the tunnel span except for the Q system. But the change rate is different. The change rate is ranked as: GSI system>BQ system>RMR system. The support pressure value of RMR system increases with the increase of the tunnel depth. But other systems are unchanged. The support pressure of Q system decreases with the increase of Jr. And the support pressure of GSI system decreases with the increase of the uniaxial compressive strength of rock. But other systems are unchanged. Comprehensive analysis shows that the sensitivity of each support pressure assessment method to different geologic parameter is different. In fact, from the analysis of the rock mass classification index, it can be seen that the influencing factors considered in each system are the same. However, different rock mass classification systems have different emphasis in determining the rock mass classification index.
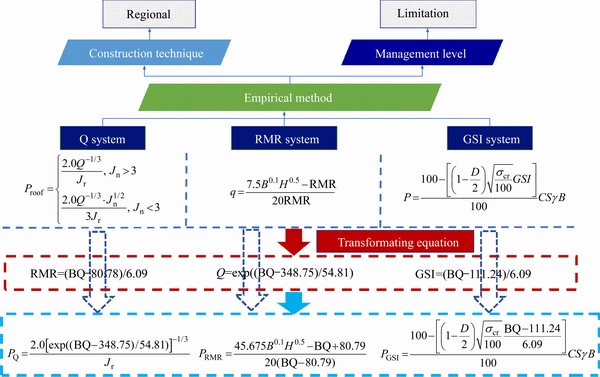
Figure 11 Analysis of different support pressure assessment method
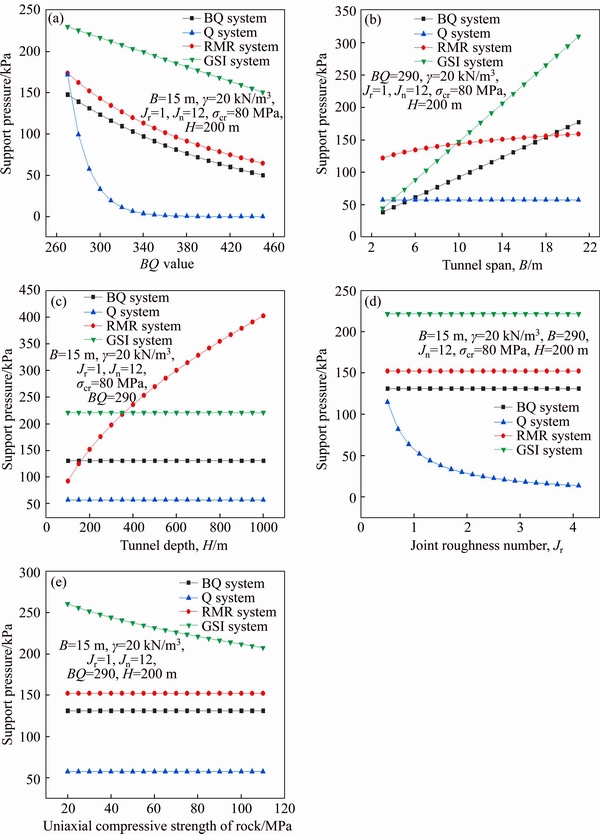
Figure 12 Relationship between support pressure and BQ value (a), tunnel span B (b), tunnel depth H (c), joint toughness Jr (d), and uniaxial compressive strength of rock (σcr) (e)
5 A design method of supporting structure based on BQ system and its rationality analysis
Estimation of support pressure is extremely important to the support system design and the construction safety of tunnels. In this paper, a new assessment method for tunnel support pressure has been proposed by considering the rock mass classification index (BQ-index). The design process of the supporting structure based on the BQ system will be analyzed in this section. And its rationality will be analyzed in detail through numerical calculations.
5.1 Design process of support structure
Recently, the hyperstatic reaction method (HRM) [62-68] has been successfully applied to determine the behavior of tunnel’s support structure. HRM is part of the numerical method category. And it has been studied by many scholars. At the same time, the rationality of the numerical method HRM is analyzed a lot. Based on this calculation method, the design process of supporting structure using the support pressure assessment method proposed in this paper will be explained. The specific design process is shown in Figure 13 as follows:
1) The tunnel geomechanical parameters are obtained through geological exploration data at first. Then the BQ value is calculated by Eq. (1). Finally, the support pressure is calculated by Eqs. (15) and (17).
2) The safety analysis of the pre-designed support parameters is carried out through the HRM model. It needs to be emphasized here that the safety factor mentioned in this article is calculated according to the safety factor calculation method in the China Railway Tunnel Design Code [69]. Due to the different calculation methods of safety factor in various countries, when evaluating the safety of supporting parameters, the calculation method of safety factors should be selected by the stands of each country.
3) Through the analysis of the safety factor, if the safety factor meets the requirements, the pre-designed support structure parameters can be applied to the actual tunnel project. If not, the pre-support parameters will be redesigned.
4) After the design parameters of the supporting structure are applied to the project, the stress and deformation of the supporting structure need to be monitored to verify the rationality of the pre-design parameters. If the tunnel construction safety requirements are not met, the pre-support parameters will be redesigned. The analysis of the safety of the support parameters is stopped until the construction safety requirements are met.
5.2 Rationality analysis
In order to verify the proposed support pressure assessment method, it is applied to a high-speed railway tunnel under construction in China.
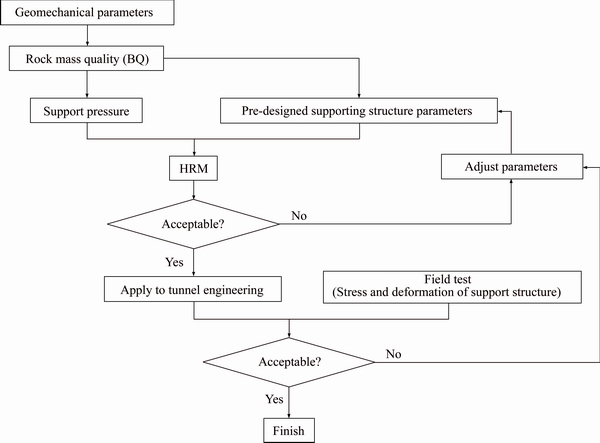
Figure 13 Design process of tunnel support parameters
5.2.1 Engineering background
Zhengwan high-speed railway starts in Xiangyang and ends in Badong. The total length of the line is about 287 km and the design speed is 350 km/h. There are 33 tunnels with a total length of 167.6 km and the tunnel ratio is 58.4% (as shown in Figure 14). The tunnels of Zhengwan high-speed railway are in the form of “one tube with two lanes” and the excavation area is about 150 m2. The length ratio of the IV and V classes of rock mass (The rock mass classes are determined according to the BQ system) is about 67.4%. It mainly covers seven kinds of lithology (as shown in Figure 15).
In order to improve the safety and quality of the construction, a full-section (Figure 16) mechanized construction design scheme has been proposed considering the geological environment and engineering situation.

Figure 14 Number of tunnels
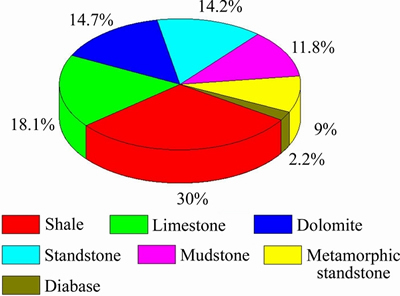
Figure 15 Percentage of mileage for each lithology
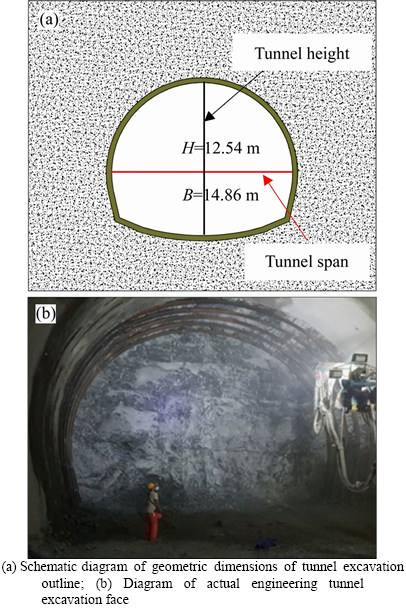
Figure 16 Full-section constructionmethod:
5.2.2 Analysis of numerical calculation results
Parameters of the tunnel in Zhengwan high-speed railway are used as a reference case in this study. The dimensions of tunnel are shown in Figure 16, and the geotechnical parameters are listed in Table 7. The tunnel is supported by a concrete lining. And the parameters of the tunnel lining are summarized in Table 7.
Through the safety analysis of tunnel support structure under the two rock mass classes (IV-BQ=350, IV-BQ=250) (as shown in Figure 17), the pre-designed support structure parameters meet the construction safety requirements and can be used in engineering.
5.2.3 Analysis of field test results
The on-site support structure forces were tested in order to verify the rationality of the support pressure assessment method. The test content covered the shotcrete stress, steel frame stress, axial force of bolts and support pressure. There were 30 test sections distributed in 6 tunnels.
Table 7 Input parameters for reference case

The distribution of test points and field tests is shown in Figure 18.
According to the analysis of test results, all the supporting structures were in safe states. The measured results are consistent with the numerical calculation result. The existing design parameters of the support structure have been optimized, and the detailed analysis results can be referred to Refs. [70, 71]. It can be seen that the design of the support structure parameters using the proposed support pressure assessment method is reasonable.
6 Discussion
The analysis of the field test data proves that the estimation method of the support pressure based on the BQ system is reasonable. However, in the process of establishing the support pressure estimation method, there are some default assumptions, which are not mentioned above, and are now described as follows.
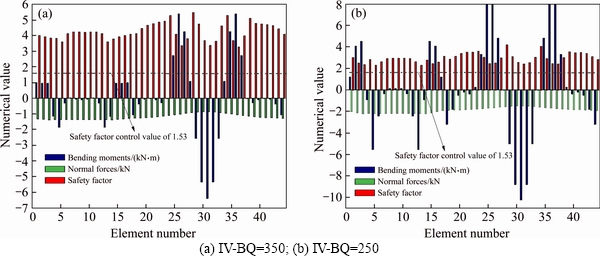
Figure 17 Safety factor and internal forces induced in tunnel lining:

Figure 18 Distribution schematic diagram of test points and field tests
1) The proposed method considers three influential parameters, namely tunnel span, rock weight and BQ-index. However, there are few descriptions of ground conditions(stress state, physical and mechanical parameters, etc.) and supporting systems.
① Ground condition: this paper assumes that the ground condition is non-squeezing and the physical and mechanical parameters are similar at the same class. The values of the physical and mechanical parameters are based on relevant specifications [47]. Therefore, this paper approximates the effect of rock mass parameters on supporting pressure with different rock mass classes.
② Support system: there is little description about the support system, including the thickness and strength of the shotcrete and the arch structure. In fact, this paper also defaults to the same support system under the same rock mass class, assuming that the rock mass has taken into account the impact of the support system. The main content of this study is estimating the support pressure under non-squeezing ground conditions (relevant assumptions have been made), and the tunnel support system under non-squeezing ground conditions (if no special instruction) is the same at the same rock mass class in China. In other words, in this paper, the estimation method of support pressure with rock mass class as variable has considered the influence of the support system.
2) The lithology of the rock mass is not described in this paper, but this paper assumes that as long as the rock mass conditions are classified in the same rock mass class, the support pressure generated is the same, regardless of the lithology of the rock mass. After all, the lithology of the rock mass has been taken into account when the rock mass class is determined.
3) As mentioned above, the data of 205 support pressure test-section in China were used for analysis, of which 97 were obtained through literatures and 108 were measured by authors. But the sample classification was based on the rock mass class. For the lithology of the rock mass, the tunnel construction method and construction machinery have not been analyzed in detail, assuming the support pressure is obtained under the same standard.
4) The calculation formula of support pressure in this paper is established by multiple nonlinear regression analysis methods. The variable used is not BQ-index, but the rock mass class. The first thing is to determine the relationship between support pressure and rock mass class. Then according to the relationship between rock mass class and BQ-index, the relationship between support pressure and BQ-index is obtained. Due to this conversion process, there will be some errors in the application of the calculation method of support pressure proposed in this paper.
There are some assumptions in the process of establishing the method, it will cause some errors in practical application. However, these errors are allowed and will not affect the application of the estimation method of support pressure proposed in this paper. And the author will make a detail analysis in the later research.
7 Conclusions
1) The support pressure assessment method is proposed based on the multiple nonlinear regression analysis on a large amount of field test data. The value of support pressure is related to the tunnel span, the weight of rock mass and BQ-index. The value of support pressure decreases with the increase of the BQ value and increase of tunnel span and weight of rock mass.
2) This paper proves that proposing a suitable support pressure assessment method for tunnels in China is necessary through the comparison with the support pressure assessment methods of RMR system, Q system and GSI system. The support pressure assessment method of BQ system is sensitive to the change of BQ value and tunnel span. The support pressure assessment method of Q system is sensitive to the change of Q value and Jr. The support pressure assessment method of RMR system is sensitive to the change of RMR value and tunnel depth. The tunnel span has some influence on RMR system, but the support pressure value changes little with the increase of the tunnel span comparing with tunnel depth.
3) The support pressure assessment has been applied to designing the parameters of supporting structure in the Zhengwan high-speed railway tunnel and the rationality of this method has been verified through the data of field test.
Contributors
The overarching research goals were developed by WANG Ming-nian, WANG Zhi-long, TONG Jian-jun, ZHANG Xiao, DONG Yu-cang and LIU Da-gang. WANG Ming-nian and LIU Da-gang provided the test data used in this paper. WANG Zhi-long proposed the calculation method of support pressure and analyzed the calculated results. The initial draft of the manuscript was written by WANG Zhi-long. TONG Jian-jun, ZHANG Xiao and DONG Yu-cang revised the errors of the initial draft. All authors replied to reviewers’ comments and revised the final version.
Conflict of interest
WANG Ming-nian, WANG Zhi-long, TONG Jian-jun, ZHANG Xiao, DONG Yu-cang and LIU Da-gang declare that they have no conflict of interest.
References
[1] TERZAGHI K. Rock defects and load on tunnel supports [M]. Youngstown, Commercial Shearing and Stamping Company, 1946. https://catalog.hathitrust.org/Record/101665 700.
[2] BAWDEN W F, HYETT A J, LAUSCH P. An experimental procedure for the in situ testing of cable bolts [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics, 1992, 29(5): 525-533. DOI: https://doi. org/10.1016/0148-9062(92)92635-P.
[3] DEERE D U, DEERE D W. The rock quality designation (RQD) index in practice [C]// Rock Classification System for Engineering Purposes. Philadelphia: American Society for Testing and Materials, 1988: 91-101. DOI: 10.1520/ STP48458S.
[4] WICKHAM G E, TIEDMANN H R. Research in ground support and its evaluation for coordination with system analysis in rapid excavation [R]. San Francisco: Jacobs Associates, 1972. https://www.zhangqiaokeyan.com/ntis- science-report_other_thesis/020711916085.html.
[5] BIENIAWSKI Z T. Rock mass classification in rock engineering [C]// Symposium Proceedings of Exploration for Rock Engineering. Johannesburg, 1976: 97-106. https:// www.scirp.org/reference/ReferencesPapers.aspx?ReferenceID=1424309.
[6] BARTON N, LIEN R, LUNDE J. Engineering classification of rock masses for the design of tunnel support [J]. Rock Mechanical and Rock Engineering, 1974, 6(4): 189-239. DOI: 10.1007/BF01239496.
[7] VOEGELE M D, FAIRHURST C. A numerical study of excavation support loads in jointed rock masses [C]// The 23rd Symposium on Rock Mechanics. Berkeley, the University of California, 1982, 673-683. DOI: ARMA-82- 673.
[8] UNAL E. Development of design guidelines and roof control standards for coal mine roofs [D]. Philadelphia: Pennsylvania State University, 1983. DOI: 10.1007/s11816- 008-0056-5.
[9] UNAL E. Rock reinforcement design and its application in mining [C]// Proceedings of International Symposium on Rock Support. Sudbury, Canada, Publ Rotterdam: A Balkema, 1992: 541-546. DOI: 10.1016/0148-9062(94)93090-2.
[10] UNAL E. Modified rock mass classification: M-RMR system [C]// Milestone in Rock Engineering, the Bieniawski Jubilee Collection. Balkema, Rotterdam, 1996: 203-223. https://www.researchgate.net/publication/290984288_Modified_rock_mass_classification_M-RMR_system.
[11] VENKATESWARLU V. Geomechanics classification of coal measure rocks vis-à-vis roof supports [D]. Dhanbad: Indian School of Mines, 1986. http://linkinghub.elsevier.com/ retrieve/pii/0148906287924132.
[12] GHOSE A K, GHOSH C N. Design of support systems-A methodological approach [C]// Proc Int Symposium on Rock Support. Sudbury, Canada, Publ Rotterdam: A Balkema, 1992. DOI: 10.1016/0148-9062(93) 92180-x.
[13] BHASIN R,GRIMSTAD E. The use of stress-strength relationship in the assessment of tunnel stability [J]. Tunnelling and Underground Space Technology, 1996, 11(1): 93-98. DOI: 10.1016/0886-7798(95)00047-X.
[14] VERMAN M. Rock mass-tunnel support interaction analysis [D]. Roorkee, India: University of Roorkee, 1993.
[15] SIGN B, JETHWA J L, DUBE A K, SINGH B. Correlation between observed support pressure and rock mass quality [J]. Tunnelling and Underground Space Technology, 1992, 7(1): 59-74. DOI: 10.1016/0886-7798(92)90114-W.
[16] PALMSTROM A. RMi-A rock mass characterization system for rock engineering purposes [D]. Norway: University of Oslo, 1995.
[17] PALMSTROM A. Characterizing rock masses by the RMi for use inpractical rock engineering, Part 1: The development of the rock mass index(RMi) [J]. Tunnelling and Underground Space Technology, 1996, 11(2): 175-188. DOI: 10.1016/0886-7798(96)00015-6.
[18] PALMSTROM A. Recent developments in rock support estimates by the RMi [J]. Journal of Rock Mechanics and Tunnelling Technology, 2000, 6(1): 1-19. http://www. rockmass.net/ap/66_Palmstrom_on_Recent_developments_RMi.pdf.
[19] GEOL R K, JETHWA J L, DHAR B B. Effect of tunnel size on support pressure [J]. International Journal of Rock Mechanics & Mining Sciences & Geomechanics, 1996, 33(7): 749-755. DOI: 10.1016/0148-9062(96)00020-4.
[20] GRIMSTAD E, BARTON N. Updating the Q-system for NMT [C]// Proc of the International Symposium on Sprayed Concrete-modern Use of Wet Mix Sprayed Concrete for Underground Support. 1993: 46-66.
[21] BHASIN R, GRIMSTAD E. The use of stress-strength relationship in the assessment of tunnel stability [J]. Tunnelling & Underground Space Technology, 1996, 11(1): 93-98. DOI: 10.1016/0148-9062(96)83597-2.
[22] BARTON N. Some new Q-value correlations to assist in site characterization and tunnel design [J]. Int J Rock Mech Min Sci, 2002, 39: 185-216. DOI: https://doi.org/10.1016/ S1365-1609(02)00011-4.
[23] ZHANG Xiao, WANG Ming-nian, WANG Zhi-long, Li Jia-wang, ZHAO Si-guang, TONG Jian-jun, LIU Da-gang. Stability analysis model for a tunnel face reinforced with bolts and an umbrella arch in cohesive-frictional soils [J]. Computers and Geotechnics, 2020, 124: 103635. DOI: 10.1016/j.compgeo.2020.103635.
[24] KASTNER H. Statik des tunnel-und stollenbaues auf der grundlage geomechanischer erkenntnisse [M]. Berlin- Gottingen, Springer, 1962. DOI: EP0161265 A1. (in German)
[25] LU Cheng, YU Li, WANG Ming-nian. Upper bound analysis of collapse failure of deep tunnel under karst cave considering seismic force [J]. Soil Dynamics and Earthquake Engineering, 2020, 123: 106003. DOI: 10.1016/j.soildyn. 2019.106003.
[26] DAEMEN J J K. Tunnel support loading caused by rock failure [D]. Minneapolis: University of Minnesota, 1975. DOI: 10.1016/0148-9062(75)90618-X.
[27] HOEK E, BROWN E T. Underground excavations in rock [M]. London: Institution of Mining and Metallurgy, 1980. DOI: https://doi.org/10.1016/0148-9062(81)90809-3.
[28] BROWN E T, BRAY J W, LANDANYI B, HOEK E. Ground response curves for rock tunnels [J]. Journal of Geotechnical Engineering, 1983, 109(1): 15-39. DOI: 10.1061/(ASCE) 0733-9410(1983)109:1(15).
[29] SHEOREY P R. Support pressure estimation in failed rock conditions [J]. Engineering Geology, 1985, 22(2): 127-140. DOI: 10.1016/0013-7952(85)90043-2.
[30] CARRANZA-TORRES C. Elasto-plastic solution of tunnel problems using the generalized form of the Hoek-Brown failure criterion [J]. International Journal of Rock Mechanics and Mining Science, 2004, 41(1): 629-639. DOI: 10.1016/ j.ijrmms.2004.03.111.
[31] OSGOUI R R, UNAL E. An empirical method for design of grouted bolts in rock tunnels based on the geological strength index (GSI) [J]. Engineering Geology, 2009, 107(4): 154-166. DOI: 10.1016/j.enggeo.2009.05.003.
[32] DEHKORDI M S, LAZEMI H A, SHAHRIAR K. Estimation of the rock load in non-squeezing ground condition using the post failure properties of rock mass [J]. Geotechnical and Geological Engineering, 2015, 33(4): 1115-1128. DOI: 10.1007/s10706-015-9891-7.
[33] VEOGELE M D, FAIRHURST C. A numerical study of excavation support loads in jointed rock masses [C]// The 23rd Symposium on Rock Mechanics. Berkeley: The University of California, 1982: 673-683. DOI: ARMA-82-673.
[34] WHITTAKER B N, SMITH S F, MATHESON G D. Influence of in-situ stress field on the stability of mine tunnels [C]// Proc ISRM Symposium: Eurock’92 Rock Characterization. London: J A Hudson, 1992: 227-232. DOI: https://doi.org/10.1016/0148-9062(93)92656-B.
[35] OSGOUI R. Development of an elasto-plastic analytical model for design of grouted rock bolts in tunnels with particular reference to poor rock masses [D]. Ankara: Middle East Technical University, 2007. DOI: https://doi.org/10. 1002/nag.823.
[36] BIENIAWSKI Z T. Engineering classification of jointed rock masses [J]. Civil Engineering South Africa, 1973, 15(12): 335-343. DOI: 10.1016/0148-9062(74)90924-3.
[37] BIENIAWSKI Z T. The geomechanics classification in rock engineering applications [C]// 4th ISRM Congress: International Society for Rock Mechanics and Rock Engineering. Montreux, Switzerland, 1979. DOI: 10.1016/ 0148-9062(80)90601-4.
[38] HASHEMI M, MOGHADDAS S, AJALLOEIAN R. Application of rock mass characterization for determining the mechanical properties of rock mass: A comparative study [J]. Rock Mechanics and Rock Engineering, 2010, 43(3): 305-320. DOI:10.1007/s00603-009-0048-y.
[39] HOEK E. Strength of rock and rock masses [J]. International Society for Rock Mechanics News Journal, 1994, 2(2): 4-16. DOI: 10.1201/b16978-9.
[40] HOEK E, KAISER P K, BAWDEN W F. Support of underground excavations in hard rock [M]. Balkema, Canberra, 1995. DOI: https://www.logobook.ru/prod_ show.php/objectuid=12674551.
[41] OSGOUI R, UNAL E. Characterization of weak rock masses using GSI-Index and the estimation of support-pressure [C]// The 40th US Symposium on Rock Mechanics (USRMS). Anchorage, Alaska: American Rock Mechanics Association, 2005.
[42] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Science, 1997, 34(8): 1165-1186. DOI: 10.1016/ S0148-9062(97)00305-7.
[43] SONMEZ H, ULUSAY R. Modifications to the geological strength index (GSI) and their applicability to stability of slopes [J]. International Journal of Rock Mechanics and Mining Science, 1999, 36(6): 743-760. DOI: 10.1016/ S0148-9062(99)00043-1.
[44] SONMEZ H, ULUSAY R. A discussion on the Hoek-Brown failure criterion and suggested modifications to the criterion verified by slope stability case studies [J]. Yerbilimleri, 2002, 26: 77-99.
[45] CAI M, KAISER P K, UNO H, TASAKA Y, MINAMI M. Estimation of rock mass deformation modulus and strength of jointed hard rock masses using the GSI system [J]. International Journal of Rock Mechanics and Mining Science, 2004, 41(1): 3-19. DOI: 10.1016/s1365-1609(03)00025-x.
[46] WANG Guang-de, SHI Yu-chuan, LIU Han-chao, KOU Jia-wei. The classification of rock mass around tunnel and underground chamber for water conservancy and hydroelectric engineering [J]. Journal of Hydroelectric Engineering, 2006(2): 123-127. DOI: 10.1061/(ASCE) 0887381X(2006)20:1(20). (in Chinese)
[47] SHEN Yan-jun, XU Guang-li, SONG Sheng-wu, LI Zhi-peng, FENG Xue-min, DONG Jia-xing. A classification method of surrounding rock mass in hydropower project in high geostress area [J]. Chinese Journal of Rock Mechanical and Engineering, 2014, 33(11): 2267-2275. DOI: 10.13722/ j.cnki.jrme.2014.11.011. (in Chinese)
[48] LIU Z X, DANG W G. Rock quality classification and stability evaluation of undersea deposit based on M-IRMR [J]. Tunnelling and Underground Space Technology, 2014, 40: 95-101. DOI: 10.1016/j.tust.2013.09.013.
[49] GB/T50218–2014. Standard for engineering classification of rock masses [S]. Beijing, the National Standards Compilation Group of People’s Republic of China. 2014. (in Chinese)
[50] XU Hong-fa, CHEN Feng, WANG Bin, HUA Zhong-min, GEN Han-sheng. Relationship between RMR and BQ for rock mass classification and estimation of its mechanical parameters [J]. Chinese Journal of Geotechnical Engineering, 2014, 36(1): 195-198. DOI: 10.11779/CJGE201401021. (in Chinese)
[51] WANG S J, LEE C F, YUE Z Q. Global quality assessment of rock works for permanent shiplock of the three gorges project on Yangtze river [J]. China Engineering Geology, 2004, 76(1, 2): 41-64. DOI: 10.1016/j.enggeo.2004.06.005.
[52] SUN Hui, ZHENG Ying-ren, WANG Zai-quan, ZHANG Li-ming. Discussion and determination to surrounding rock classification of metal mine [J]. Procedia Engineering, 2011, 26: 1740-1748. DOI: 10.1016/j.proeng.2011.11.2362.
[53] YU Wei-jian, GAO Qian, HAN Yang, ZHANG Zhou-ping. Non-linear coupling classification technique of surrounding rock mass and its application in Jingchuan Mine [J]. Chinese Journal of Geotechnical Engineering, 2008, 30(5): 663-669. DOI: 10.3901/JME.2008.10.294. (in Chinese)
[54] FENG X T, ZHANG C, QIU S, ZHOU H, JIANG Q, LI S. Dynamic design method for deep hard rock tunnels and its application [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2016, 8: 443-461. DOI: 10.1016/j.jrmge.2016. 01.004.
[55] CHEN X, XU Z. The ultrasonic P-wave velocity-stress relationship of rocks and its application [J]. Bulletin of Engineering Geology and the Environment, 2017, 76: 661-669. DOI: 10.1007/s10064-016-0866-6.
[56] SHEN Yan-jun, YAN Rui-xin, YANG Geng-she, XU Guang-li, WANG Shan-yong. Comparisons of evaluation factors and application effects of the new [BQ] GSI system with international rock mass classification systems [J]. Geotechnical and Geological Engineering, 2017, 35: 2523-2548. DOI: 10.1007/s10706-017-0259-z.
[57] LIU Quan-sheng, LIU Jian-ping, PAN Yu-cong, KONG Xiao-xuan, HONG Kai-rong. A case study of TBM performance prediction using a Chinese rock mass classification system–Hydropower classification (HC) method [J]. Tunnelling and Underground Space Technology, 2017, 65: 140-154. DOI: 10.1016/j.tust.2017.03.002.
[58] KOMURLU E, DEMIR S. Use of rock mass rating (RMR) values for support designs of tunnels excavated in soft rocks without squeezing problem [J]. GeoScience Engineering, 2019, 2: 1-17. DOI: 10.35180/gse-2019-0007.
[59] WU A, LIU F. Advancement and application of the standard of engineering classification of rock masses [J]. China Journal Rock Mechanical Engineering, 2012, 31(8): 1513-1523.
[60] BIENIAWSKI Z T. Engineering rock mass classifications: A complete manual for engineers and geologists in mining, civil, and petroleum engineering [M]. Toronto: John Wiley and Sons, 1989.
[61] HOEK E, BROWN E T. Practical estimates of rock mass strength [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34(8): 1165-1186. DOI: 10.1016/ S0148-9062(97)00305-7.
[62] DO N A, DIAS D, ORESTE P P. The behaviour of the segmental tunnel support studied by the hyperstatic reaction method [J]. European Journal of Environmental, 2014, 18(4): 489-510. DOI: 10.1080/19648189.2013.872583.
[63] DO N A, DIAS D, ORESTE P P, DJERAN-MAIGRE I. A new numerical approach to the hyperstatic reaction method for segmental tunnel linings [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(15): 1617-32. DOI: 10.1002/nag.2277.
[64] ORESTE P. A numerical approach to the hyperstatic reaction method for the dimensioning of tunnel supports [J]. Tunnelling and Underground Space Technology, 2007, 22(2): 185-205. DOI: 10.1016/j.tust.2006.05.002.
[65] ORESTE P, SPAGNOLI G, CERAVOLO L A. A numerical model to assess the creep of shotcrete linings [J]. Geotechnical Engineering, 2019, 172(4): 344-354. DOI: 10.1680/jgeen.18.00089.
[66] ORESTE P, SPAGNOLI G, RAMOS CA L. Evaluation of the safety factors of shotcrete linings during the creep stage [J]. Geotechnical Engineering, 2020, 173(3): 274-282.
[67] ORESTE P, SPAGNOLI G, RAMOS C A L. The elastic modulus variation during the shotcrete curing jointly investigated by the convergence-confinement and the hyperstaticreaction methods [J]. Geotechnical and Geological Engineering, 2019, 37: 1435-1452. DOI: 10.1007/s10706-018-0698-1.
[68] ORESTE P, SPAGNOLI G, RAMOS CA L. Assessment of the safety factor evolution of the shotcrete lining for different curing ages [J]. Geotechnical and Geological Engineering, 2019, 37(6): 5555-5563. DOI: 10.1007/s10706-019- 00990-2.
[69] TB10003-2016. Code for design on tunnel of railway [S]. Beijing: China Railway Publishing House, 2016. (in Chinese)
[70] WANG Zhi-jian. Research on key technology of large cross-section mechanized construction of Zheng-Wan high-speed rail way [J]. Tunnel Construction, 2018, 38(8): 1257-1270. (in Chinese)
[71] JIN Qiang-guo. Optimization of support design of large- scale mechanized construction of Zhengzhou-Wanzhou high- speed railway tunnel [J]. Tunnel Construction, 2018, 38(8): 1324-1333. (in Chinese)
(Edited by FANG Jing-hua)
中文导读
基于BQ指标的深埋铁路隧道支护压力评估方法
摘要:支护压力的评估对于支护结构系统的设计及隧道施工的安全至关重要。目前,有较多基于不同岩体分类系统的支护压力评估方法,例如Q系统,GSI系统和RMR系统等。但各种岩体分类系统都是基于不同地区的隧道地质条件建立起来的。因此,每种岩体分类系统都具有一定的区域性。自BQ-Inex(BQ系统)出现以来,在中国岩石工程领域得到了广泛的应用。但是中国仍然没有以BQ指数为参数的支护压力评估方法。本文基于中国54条铁路隧道的现场试验数据,采用多元非线性回归分析方法,考虑隧道跨度和围岩重度,提出了一种基于BQ指标的支护压力经验评估方法。然后,通过与国际上广泛使用的RMR系统,Q系统和GSI系统的支护压力评估方法的比较和分析,阐述了建立以BQ指标为参数的支护压力评估方法对保证中国隧道施工安全的意义和必要性。最后,将基于BQ指标的支护压力经验估算方法应用于中国高速铁路隧道-郑万高铁支护系统设计中,并通过实测数据验证了该方法的合理性。
关键词:岩体分级;支护压力;深埋隧道;现场测试;多元非线性回归;BQ指标
Foundation item: Projects(51878567, 51878568, 51578458) supported by the National Natural Science Foundation of China; Projects(2017G007-F, 2017G007-H) supported by China Railway Science and Technology Research and Development Plan
Received date: 2020-01-19; Accepted date: 2020-07-28
Corresponding author: LIU Da-gang, Professor, PhD; Tel: +86-18328369275; E-mail: zlwang@my.swjtu.edu.cn; ORCID: https:// orcid.org/0000-0002-3740-2340
Abstract: Estimation of support pressure is extremely important to the support system design and the construction safety of tunnels. At present, there are many methods for the estimation of support pressure based on different rock mass classification systems, such as Q system, GSI system and RMR system. However, various rock mass classification systems are based on different tunnel geologic conditions in various regions. Therefore, each rock mass classification system has a certain regionality. In China, the BQ-Inex (BQ system) has been widely used in the field of rock engineering ever since its development. Unfortunately, there is still no estimation method of support pressure with BQ-index as parameters. Based on the field test data from 54 tunnels in China, a new empirical method considering BQ-Inex , tunnel span and rock weight is proposed to estimate the support pressure using multiple nonlinear regression analysis methods. And then the significance and necessity of support pressure estimation method for the safety of tunnel construction in China is explained through the comparison and analysis with the existing internationally widely used support pressure estimation methods of RMR system, Q system and GSI system. Finally, the empirical method of estimating the support pressure based on BQ-index was applied to designing the support system in the China’s high-speed railway tunnel—Zhengwan high-speed railway and the rationality of this method has been verified through the data of field test.


