J. Cent. South Univ. (2018) 25: 218-229

DOI: https://doi.org/10.1007/s11771-018-3731-x

Effective stress law for rock masses and its application in impoundment analysis based on deformation reinforcement theory

CHENG Li(程立)¹, LIU Yao-ru(刘耀儒)¹, PAN Yuan-wei(潘元炜)², YANG Qiang(杨强)¹, LV Zheng(吕征)¹

1. State Key Laboratory of Hydroscience and Hydraulic Engineering (Tsinghua University),Beijing 100084, China;

2. Schlumberger Technologies (Beijing) Ltd., Beijing 100015, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract:

Reservoir impoundment is related to several hydraulic engineering concerns, including irreversible valley contractions, landslides and reservoir-induced earthquakes. However, these phenomena, such as valley contractions, are hardly to be explained by the conventional method. The scientific understanding of water effects during impoundment and their hazards to hydraulic structure are needed. The effective stress law for fissured rock masses is introduced in the elasto-plastic model employing the Drucker-Prager criterion and implemented in the three dimension (3D) nonlinear finite element method (FEM) program Three-dimensional FINite Element (TFINE). The slope deforms towards river-way during impoundment since the increasing pore pressure in fissures changes stress state and leads to additional plastic deformation in the rock materials. The value of Biot coefficient and the influence of water on rock materials are discussed in detail. Thus, the mechanism of slope deformation during the impoundment of Jinping-I arch dam is revealed, and the deformation is accurately measured. The application of the effective stress law provides a method to consider stress assessment, deformation evaluation and stability estimate of hydraulic structures during the impoundment process. This is a beneficial exploration and an improvement of hydraulic engineering design.

Key words:

effective stress law; elasto-plastic FEM model; Biot coefficient; impoundment; valley contractions；

Cite this article as:

CHENG Li, LIU Yao-ru, PAN Yuan-wei, YANG Qiang, LV Zheng. Effective stress law for rock masses and its application in impoundment analysis based on deformation reinforcement theory [J]. Journal of Central South University, 2018, 25(1): 218–229.

1 Introduction

Lifecycle of dam-foundation system in hydraulic engineering is a process of non- equilibrium evolution consisting of excavation, concrete pouring, impoundment and long-term operation. In each period of the lifecycle, the system may be deviated from equilibrium state due to the disturbances of either artificial or inartificial factors. The main factor and driving force of non- equilibrium evolution during excavation is the released load [1]. As for long-term operation period, material strength and stiffness degradation is the dominating factor of long-term deformation. Because of the multi-effects of water level rising, the initial impoundment is more complicated than the other periods. The process of reservoir impoundment is related to several engineering concerns, including valley width contraction, landslides and reservoir-induced earthquakes [2]. Researchers have been improving the scientific understanding of water effects and their hazards to hydraulic structures with theories and numerical methods developed. Now some researchers realize that impoundment is a complicated integrated process accompanied with several mechanisms, such as material degradation and the effective stress law [3, 4]. Thus initial impoundment period cannot be interpreted as a consequence of just one single factor as before in the lifecycle of hydraulic structures.

Slope and foundation deformation during the initial impoundment is related to some serious concerns of hydraulic engineering, such as embankment erosion, landslides, earthquakes and their influences to dam body. Vajont dam is a typical hydraulic project suffering from reservoir- induced landslide in the 3rd year of the initial impoundment, numerous investigations on the case of Vajont dam have been undertaken [5, 6], subsequently. Most relevant literatures on impoundment effects are focused on potential bank failure and landslides at present. But another reservoir induced phenomenon, valley contractions, may also affect the hydraulic structure stability and cause hazard of local failure. As water level rising, slopes tend to deform towards the river side and make valley contract. This common phenomenon during reservoir impoundment was firstly found in the construction and operation of some European arch dams. Some other typical projects include the Kurobe dam in Japan [7] and some 300 m-level high arch dams in China, such as Lijiaxia [8],Ertan [9], Jinping-I [10] and Xiluodu arch dam [11]. Valley contraction causes additional thrust on the arch abutment and changes ambient stress, this phenomenon may also explain why the dam body displacements of numerical simulation are far from observed values during impoundment.

Interests in the impoundment process are increasing from year to year, but literatures about reservoir-induced slope deformation are limited in the groundwater level fluctuations and rainfall [12]. Some researchers applied pore pressure in the anti-sliding stability assessment of slope, but this application is based on the rigid limiting equilibrium method and is limited in elastic and two-dimensional problems [13]. Engineering concerns on the safety assessment of impoundment process require scientific description, accurate and practical evaluation method on slope deformation and valley contraction, especially for large-scale hydraulic engineering.

The phenomena observed during the impoundment process of hydraulic structures are introduced with primary analysis. The effective stress law of fissured rock masses is proposed and water effects on rock masses are demonstrated. The effective stress law for the elasto-plastic model based on the Drucker-Prager criterion is implemented in the 3D nonlinear FEM program TFINE to take advantages of FEM’s high accuracy in displacement analysis. A case study of Jinping-I high arch dam shows good agreements between the calculated and observed displacements.

The compressive stress used throughout this work is negative while valley width shrinkage is negative.

2 Phenomena of valley contraction during impoundment

2.1 Kurobe arch dam

Kurobe dam, at a height of 186 m, is the tallest dam in Japan. The calculated values of the crown cantilever deformation, with hydrostatic pressure and temperature variation considered, were compared with observed values by TEZUKA et al [7]. The maximum difference between the observed and calculated values was as lage as 15 mm. In order to find out the dominating factor of the differences, chord length and valley width of the hydro-junction area had been observed since 1981. Data from 4 measuring lines indicated that valley width decreased by 10 mm magnitude when water level rose. The valley contractions made the dam deform towards upstream in contrast to the effects of hydrostatic pressure on the dam surface. It is the reason why the inversion elasticity modulus of dam concrete is much larger than that of common understanding in engineering practices.

2.2 Ertan arch dam

Ertan arch dam is another super high arch dam with a height of 240 m, located on the Yalong River, Sichuan Province, China. The valley width variations during construction and the initial impoundment are shown in Table 1. The measuring lines AN1–AN2 and AN3–AN4 are about 37 m and 50 m away from the dam axis downstream, respectively. In May 1998, the month of the initial impoundment starting, the average length of both lines decreased by 1.6 mm and 2.4 mm, respectively. The data in Table 1 represent the downstream valley width contraction, and values of the upstream valley width are expected to be more sensitive to the fluctuations of water level.

Table 1 Valley width variation of Ertan arch dam

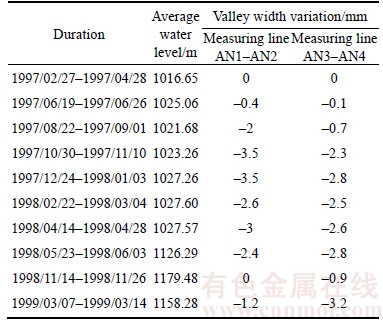
2.3 Xiluodu arch dam

Xiluodu arch dam is another super high arch dam with a height of 285.5 m, located on the Jinsha River, China and completed in 2014. The measure lines in the both upriver and downriver all contracted at the same degree (about 40 mm). Furthermore, the valley contracted steadily during impoundment and did not reveal any descending trend when water level declined.

2.4 Discussion

The valley contractions of Xiluodu arch dam are quite different from those of other arch dams for they contracted at 40 mm (much larger than others) both upriver and downriver.

During impoundment, hydrostatic pressure on the upstream dam surface increases the thrusts on the dam abutments, and makes downstream valley expand instead of contracting. As shown in Figure 1, hydrostatic pressure on the slope surfaces is a considerable instantaneous load shortly after impoundment. In a few days, groundwater level rises and the hydrostatic pressure on slope surfaces is transformed into the seepage force.

The seepage force increments caused by rising of water level are towards the slope side in the upstream region and the river-way side in the downstream region. So the valley width increases in the upriver and decreases in the downriver, which is also on the contrary of the observed values. The buoyancy forces are usually considered as an additional term vertically up of the seepage forces.

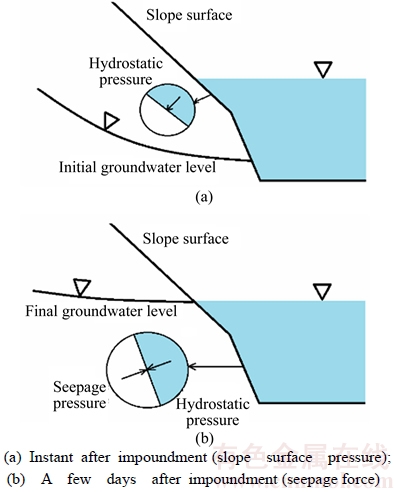
Figure 1 Conceptual model of water effects induced by reservoir impoundment:

Thus valley contraction induced by the reservoir impoundment is not a consequence of water hydrostatic pressure, seepage force or buoyancy force. The real reason would be explained hereinafter.

3 Mechanism of water effects during impoundment

3.1 Effective stress law

This section proposes a scientific understanding of reservoir-induced slope deformation from the viewpoint of the effective stress law. The primitive concept of the effective stress was proposed by TERZAGHI [14] in 1923 and used to analyze the pore pressure effects on porous geotechnical materials. Terzaghi’s work was restricted to one-dimensional or two-dimensional problems under constant loads. BIOT [15] generalized this law to three-dimensional cases, and the effective stress could be expressed as:

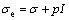                              (1)

where σ_e, σ, I and p are the effective stress tensor, total stress tensor, unit tensor and pore pressure, respectively. Biot’s theory is based on several assumptions, including 1) linearity and reversibility of stress–strain relations; 2) small strains; 3) contact areas between grains being sufficiently small; 4) hydrostatic pore pressure. However, the theoretical accuracy and validity of Eq. (1) were doubted by some investigators, especially when it came into fissured rock masses.

3.2 Derivation and experiments of Biot coefficient

Based on experimental results, GEERTSMA [16] and SKEMPTON [17] independently suggested a coefficient α in the pore pressure term of Eq. (1) as

                            (2)

where α is the effective stress coefficient, also known as Biot coefficient. They suggested α=1–K/K_s and 0<α<1, where K and K_s were the bulk moduli of material and grain, respectively. When the material compressibility was much greater than that of grain (K<<>_s), then α≈1 and Eq. (2) is degraded into Eq. (1). A rigorous derivation of α=1–K/K_s is provided by NUR et al [18], and verified by experimental results. Equation (2) described the measured strains of sandstone and granite samples accurately.

Afterwards, researchers found that α is related to porosity, but the accurate mechanism is still blur. Therefore, empirical equations describing this relation mostly take porosity as an independent variable [19]. GARAT et al [20] proposed a continuous expression of Biot coefficient as:

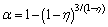                        (3)

where η is the porosity of rock material.

The above works were questioned because of a lack of theoretical verification. SUKLJE [21] proposed another derivation of α.

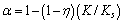                      (4)

But it is not that widely accepted for now.

The effective stress law reveals that the deformation problem in porous materials considering pore pressure can be reduced to nonporous materials by replacing the stress tensor with effective stress tensor in the constitutive relation. In contrast, the stress and strain tensors could be determined by pore pressure and material parameters with pore pressure ignored.

Pore pressure in fissures and in pores could be simultaneously considered in rock materials. CHEN et al [22] proposed a more generalized model by combining the double-porosity model and the effective stress law. A typical expression of the effective stress for double-porosity system is

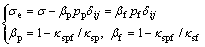           (5)

where κ_sp, κ_sf and κ_spf are the bulk compressibility moduli of solid-pore, solid-fissure and solid-pore- fissure systems, respectively. In particular, if volume of fissures vanished and p_p=p_f=p, then κ_spf=κ_sp and κ_sf=κ_s. Hence, α=β_p+β_f=1–κ_sp/κ_s and Eq. (5) would be degraded into Eq. (2). The description of double-porosity model is closer to the actual situation of rock masses, but porosity and distributions of fissures still need in-situ experiment data.

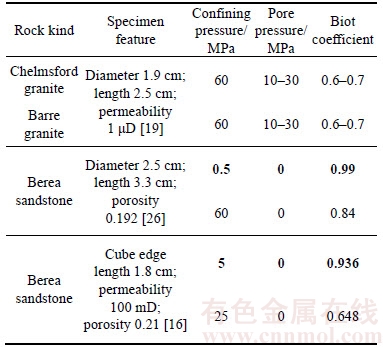
Since the effective stress law is proposed, numerous experimental investigations have been performed on Biot coefficient. Two different methods are commonly used in the measurement of Biot coefficient, one was inspired by WALLS et al [23] and the other was inspired by WALSH [24]. Experiments on different rock materials are conducted with different confining pressure and pore pressure by CHRISTENSEN et al [25]. BERNABE [26] measured the permeabilities of Chelmsford granite and Barre granite, and concluded that Biot coefficient decreased with increasing confining pressure but increased with increasing pore pressure. BERNABE [26] also explained the absence of anisotropy effects on the measured values of Biot coefficient in the light of crack configuration. Some of the above experimental results are listed in Table 2.

As stated above, Biot coefficient can be expressed as a function of material and grain bulk moduli, while rock compressibility depends not only on porosity, but also on pore shape. Therefore, equations taking porosity as only an independent variable are empirical and incomplete. The expression of Biot coefficient is recommended to use material and grain bulk moduli instead of porosity, because the former is characterized by rigorous derivation and convenient to be measured.

Table 2 Experimental results of Biot coefficient measurement

3.3 Applications of effective stress law in engineering

The effective stress law is applied in hydraulic engineering, seismic analysis, petroleum and mining engineering. However, most of these applications are for two-dimensional and elastic cases; meanwhile, the mechanism and scientific importance of the effective stress law have never been completely interpreted in engineering, especially nonlinear analyses for high arch dams.

ELLSWORTH [27] attempted to explain reservoir-induced earthquake from the perspective of the effective stress law:

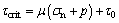                       (6)

where τ_crit is the critical shear stress; μ is the coefficient of friction; σ_n is the normal stress; p is pore pressure and τ₀ is cohesion. Pore pressure increasing rapidly induced by impoundment or injection into the underground [27] may change the ambient stress of faults and raise potential risk of catastrophic earthquake. Equation (6) is an application of the effective stress law essentially in two-dimensional problems.

The pore pressure in anti-sliding stability design of gravity dams is another case of application. Similar to the pore pressure in Eq. (6), the expression of anti-sliding safety factor suggested by the Chinese design specification of concrete dams is

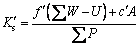                    (7)

where f′ is the friction coefficient, 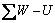is the total normal component of all loads on the hypothetical sliding surface, U is the uplift force by pore pressure, c′ is cohesion, A is the contact area

and 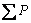is the total tangential thrust. The safety

factor 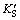is determined by factors including pore pressure, contact area and a coefficient similar to Biot coefficient. This coefficient is related to hydraulic conductivity and rock mass joints in the foundation and slope, and ranges between 0 and 1. It is approximately 1 for soft and jointed rock masses. TERZAGHI’s experiments [28] proved that it was also close to 1 for concrete. This method is also known as rigid body limit equilibrium method and widely applied in hydraulic structures.

The treatment of pore pressure in anti-sliding stability design of arch dam abutment is similar to that of gravity dam. On the upstream sliding surface of a sliding block, the pore pressure serves as a part of opening sliding surface. On the sliding surface, pore pressure is a reduction of normal stress and increases risks of sliding.

TIZDEL [29] proposed that the complex compressive and tensile deformation in the foundation of high dams was depended on both the structural construction process and the weight of reservoir water. TIZDEL' defined the saturated rock masses of slopes in the upper reservoir as a deconsolidation zone. In the deconsolidation zone, water filling in the fissures of rock masses exerts a uniform pressure from all sides, not only consolidating it, but also uplifting it. The internal boundary of deconsolidation zone is the outer boundary of zone considering water effects in the hydro-junction. To consider water effects induced by reservoir impoundment, it is important to investigate the hydraulic conductive faults and fractures for transmitting pore pressure. In fact, water flows rapidly and widely through faults and fractures. To be specific, a depth of hundreds of meters can be reached in a few days after impoundment. Therefore, it is difficult to find a distinct boundary of deconsolidation zone.

Above all, the effective stress law is mainly used in the limit analysis to estimate safety factors, even just in elastic analysis, and the research problems are two-dimensional primarily in the conventional methods. But, deformation and stability in the plastic state of three-dimension problems are seldom mentioned before which are urgently needed in hydraulic structures.

4 Implementation effective stress law into nonlinear elasto-plastic FEM

The effective stress law above-mentioned is mainly restricted to elastic and two-dimensional problems. In elastic model, the effective law is spontaneously taken into account by applying seepage force in saturated rock masses. The buoyancy-induced deformation in hydrostatic condition is included in the deformation calculated by considering effective stress law. However, rock masses sustain the enormous weight of mountains and violent tectonic movements in natural conditions in Southwest China, and a wide range of rock materials are in the critical yield condition, such as faults and joints. A slight disturbance may cause continuous irreversible plastic flow until a new balanced state is achieved or final failure occurs. Therefore, a generalization from elastic model to elasto-plastic model is urgently needed.

Such efforts have been made by a number of investigators. de BUHAN et al [4] discussed the validity of the effective stress concept in assessing the strength reduction of saturated porous materials. XIE et al [30] introduced a modification function in the hardening function of GURSON’s criterion [31], which was dependent on the degree of saturation. In this section, a simple but effective generalization of effective stress law is proposed and implemented in the nonlinear FEM.

In the nonlinear elasto-plastic iterations, as shown in Figure 2, if the elastic trial stress exceeds the yield surface, it will be adjusted until the final stress satisfies the yield criterion. In such iterative steps, the plastic strain accumulates. In other words, the part of the trial stress exceeding the yield surface is the driving force of structural plastic deformation.

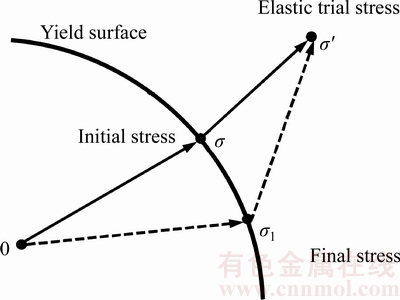
Figure 2 Elasto-plastic iteration induced by pore pressure increasing

With the effective stress law considered, two widely used cone-shaped yield criteria, Mohr- Coulomb criterion and Drucker-Prager criterion, are expressed as follows, respectively:

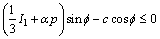               (8)

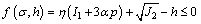            (9)

where I₁ is the first invariant of stress tensor, I₁=σ_kk; J₂ is the second invariant of deviatoric stress tensor, 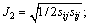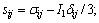θ_σ is the Roder angle, c and f are the cohesion and internal friction angle, respectively. η and h are the strength parameters related to c and f. The pore pressure term p reduces the normal compressive stress or the first invariant of stress tensor I₁. If the initial stress state is on the yield surface or close to it, the trial stress would exceed the yield surface as pore pressure increases, and stress state will be adjusted back to the yield surface, as shown in Figure 2. The consequence is an additional plastic deformation of the slope and structure.

YANG et al [32] and LIU et al [33] proposed the deformation reinforcement theory (DRT) and deduced a practical nonlinear elasto-plastic incremental method based on the Drucker-Prager criterion. The integration algorithm is of first-order accuracy and converges both small load steps and large load steps. Therefore, the algorithm is suitable and effective for large-scale geo-mechanical structure analysis.

The derivational process of stress adjustment is based on the associated flow rule and equivalent to the closest point projection algorithm for the Drucker-Prager criterion. The derivational result of the final stress σ₁ is

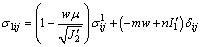           (10)

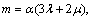
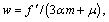
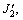
where 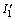and f′ are all determined by the elastic trial stress σ′, and λ and μ are Lame constants.

It can be concluded from Eq. (10) that the pore pressure just changes the value of the adjusted stress instead of the direction of plastic deformation. In other words, the directions of plastic deformation would not change but the values increase.

With pore pressure introduced into the Drucker-Prager criterion, the calculation procedures of slope and foundation deformation induced by impoundment can be concluded as follows and shown in Figure 3.

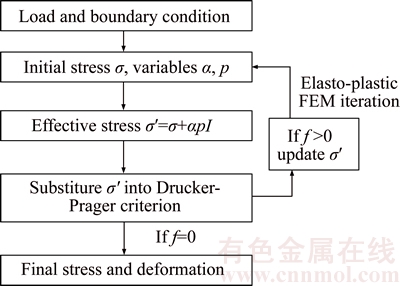
Figure 3 Implementing effective stress law in nonlinear FEM iterations

1) Apply loads and boundary conditions, including geo-stress, the dam construction condition, reservoir water level variations, hydrostatic pressure, silt pressure and temperature load.

2) Calculate the global stress field σ in the nonlinear elastio-plastic FEM.

3) Obtain the Biot coefficient α and pore pressure p of each material.

4) Calculate the value of yield function f according to Eq. (9). If f >0, the elasto-plastic iterations would go on until the final structural equilibrium is achieved, then the final deformation would be obtained.

The above method has been implemented in 3D nonlinear FEM program TFINE developed by Tsinghua University, China.

5 Application of effective stress law in Jinping-I arch dam

5.1 Introduction and analyses of Jinping-I arch dam

Jinping-I super high arch dam has the intricately topographical and geological conditions. Faults and dykes with different lithologies and scales are formed in the hydro-junction, especially the left bank slope. Therefore, the deformation and stability of slope during construction and impoundment are the most concerned problems in design and construction, which are related to the hazard assessment of high arch dam body. As shown in Figure 4, a number of slope displacement monitoring points are arranged with serial numbers marked on the left bank during excavation and construction.

Figure 4 Distribution of slope displacement monitoring points on left bank

The FEM grid includes 415439 nodes and 395959 elements consisting of wedges and hexahedrons, with a range of 2330 m (transverse direction)×2340 m (longitudinal direction)×1400 m (vertical direction). Faults f2, f5, f8, f42-9, fw and lamprophyre vein x in the left bank and faults f13, f14 and f18 in the right bank are simulated as shown in Figure 5. Moreover, engineering reinforcement measures are also modeled, including consolidation grouting, concrete replacement, anti-shear tunnels, dam heel and pedestal.

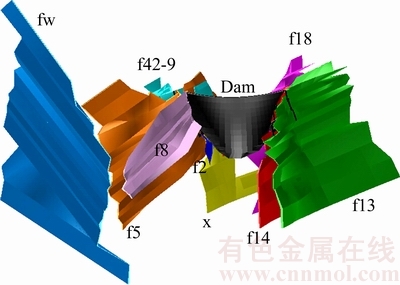
Figure 5 Jinping-I arch dam body and distributions of faults

The impoundment process is shown in Figure 6, and 2 impoundment stages are simulated which are from 2013-08-15 to 2013-12-15 and from 2013-12-15 to 2014-09-15, respectively. Water levels at the beginning and the end of the 1st stage are 1800 m and 1840 m while they are 1840 m and 1880 m in the 2nd stage.

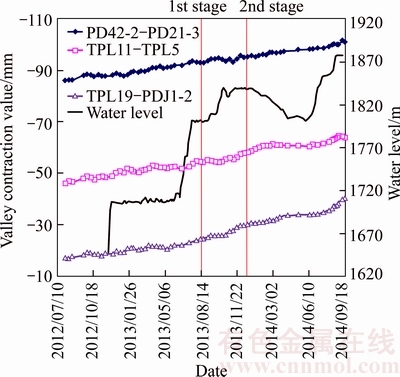
Figure 6 Water level fluctuations and monitoring results of valley contractions of Jinping-I

The beginning and ending times are selected when water levels have been stable for a few days. The time-dependent deformation is thought to be negligible for simplification and the monitoring displacements are mainly induced by impoundment process as the duration is relatively short.

Table 3 shows the mechanical parameters for numerical simulations which are the inversion values according to the monitoring displacements of the forward inverted plumb monitoring points. The parameter inversion is based on the direct method and the measured deformation of dam body to reflect the real work condition.

Table 3 Inversion mechanical parameters of concrete and rock materials for numerical calculation

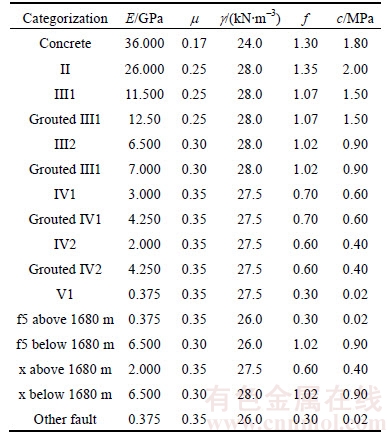
Table 2 shows the results of Biot coefficient experiments for different rock materials. In-situ experiments suggested that permeabilities of different rock masses of Jinping-I range from 0.01 D to 1 D. Permeability is a manifestation of porosity and pore shape. The in-situ rock material permeability is much greater than that of test specimens and in-situ ambient stress is no more than 20 MPa generally (it could reach 35 MPa in the extreme condition) in Jinping-I hydro-junction area, hence, assuming α≈1 in the calculation of Jinping-I arch dam is reasonable according to Table 2.

To demonstrate the valley contraction phenomenon, 5 typical measuring lines between two riversides are selected. As shown in Figure 7, PDJ1-2–TPL19, TP11–TPL5 and PD21-3–PD42-2 are above the dam crest elevation near the dam axis while TPRKP29-2-1–TPLKP29-1-1 and TPRKP29- 4-1–TPLKP29-2-1 are below the dam crest elevation downstream, the above-mentioned five measuring lines are named 1, 2, 3, 4 and 5 for convenience, respectively.

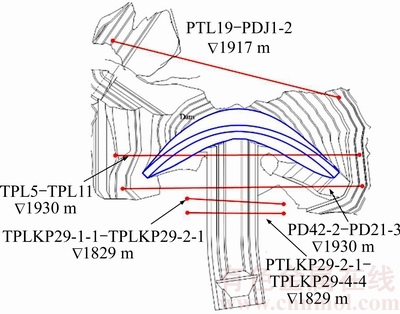
Figure 7 Distributions of valley width measuring lines

5.2 Observed and calculated values of slope deformation

The creep deformation might be neglectable as the impoundment duration is relatively short, so the water effects during impoundment could be interpreted as a combination of variations of hydrostatic pressure, seepage force and pore pressure.

The calculated values of slope displacements compared with the observed values for α=1 in the 1st stage are shown in Figure 8. The negative values denote slope deforming towards the river. Besides that, there are five measuring lines for the observation of valley width variations. The results of valley width variations in the 1st stage and the 2nd stage are shown in Figure 9, and the negative values indicate the decreasing of valley width.

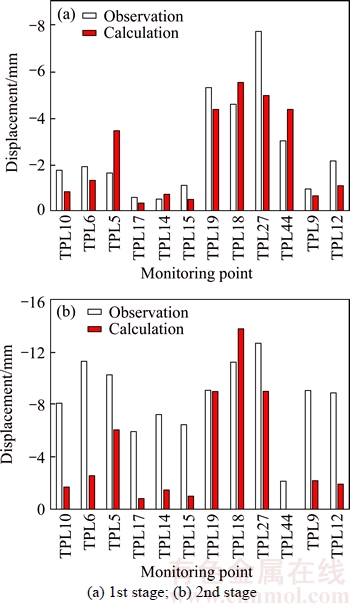
Figure 8 Observed and calculated slope displacements of monitoring points:

The results show that the calculated values agree well with the observed values, especially valley width contractions and slope displacements in the 1st stage. The calculated and observed slope displacements in the 2nd stage are towards the same direction, but the calculated values are much smaller than the observed values in some monitoring points. The reason is that the duration of the 2nd stage is about 10 months, so the rheologic deformation and topping deformation are more obvious than the 1st stage. Meanwhile, a period of drawdown from 1840 m to 1800 m and a period of rising from 1800 m to 1880 m exist in the 2nd stage, so the observed values may be thought to be the results of rising from 1800 m to 1880 m instead of rising from 1840 m to 1880 m because the displacements during drawdown are too small to be neglected. This question needs further research.

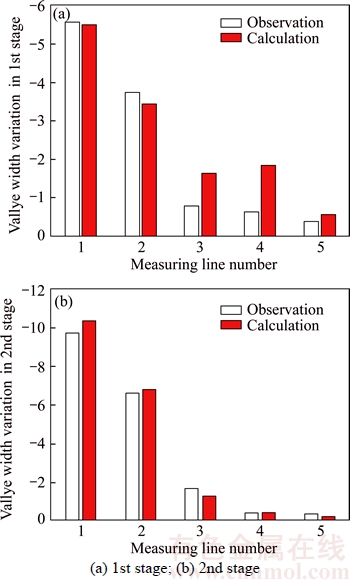
Figure 9 Observed and calculated values of valley width variations:

Effective stress law is the dominating factor of the slope deformation and valley contractions during impoundment while effects of hydrostatic pressure and seepage force could be ignored. For example, the hydrostatic pressure results in the Line 1 contracting only 0.1 mm while the calculated value considering effective stress law is 5.56 mm in the 1st stage. When water level rises and pore pressure increases, the generalized effective stress beyond the yield criterion leads to additional plastic deformation and slope deforming towards the river, so the observed deformation values are irreversible.

5.3 Influence of slope deformation on arch dam body

Dam displacements and stress states are directly influenced by slope and foundation deformation. The displacement increments for α=1 on the upper side of the dam at the crest elevation (elevation of 1885 m) in the 1st stage are shown in Figure 10, decomposed according to different influence factors: hydrostatic pressure, seepage and pore pressure. As stated above, considering the effective stress law contributes to the most of the valley width contraction. Despite that, hydrostatic pressure is the dominating factor of dam displacements during impoundment. It is also reasonable that the hydrostatic pressure on the upper side of dam surface causes most of the displacements of the crown cantilever. Seepage causes uniformly distributed deformation on the dam body. The influence of considering effective stress law on the displacements of dam body is relatively small.

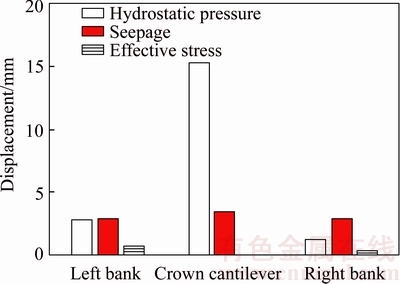
Figure 10 Displacement increments of upstream dam surface at crest elevation in 1st stage

The variations of tensile stress are mainly concentrated on the dam heel. The maximum tensile stress variation of the dam heel reaches 1.50 MPa (tensile stress increases). The conclusion can be obtained that adopting effective stress law could squeeze the dam body and worsen the stress state obviously comparing with only considering the hydrostatic pressure and seepage force. So it is very necessary to introduce effective stress law into the analysis of the safety and stability of slope and dam body during the reservoir impoundment.

Generally speaking, adopting effective stress law into the yield criterion results in additional plastic deformation of slopes and foundation and changes of displacements and stress state of the dam body. These effects are highly localized in the dam abutment especially on the left of dam base surface. Therefore, special attentions are needed for these regions and some specific reinforcements are necessary, which call for further research.

6 Discussions

The application of the effective stress law in hydraulic structures reveals an approach to taking impoundment process into consideration when evaluating stress, deformation and stability of the project. The case of Jinping-I arch dam discussed in this work adopts some simplifications. For example, the Biot coefficient is assumed to be 1 in the inundation zone of reservoir and the slope creep is ignored. The former is a reasonable assumption because of the higher permeability and lower ambient stress of in-situ rock masses in the hydro-junction area of Jinping-I than the lab experimental results. But in cases of other engineering structures, Biot coefficients for different materials should be investigated and confirmed before calculation. It is a complicated but important work because some in-situ tests are necessary. Meanwhile, slope creeps deform towards the river the same as the adopting effective stress law, so the calculated values could become smaller when ignoring slope creeps. The above two simplifications might cancel each other, so it is reasonable that the calculated values match well with the observed values.

For saturated porous material, the effective stress law is taken into consideration by applying seepage force and buoyancy force without plasticity in the conventional method. If ambient stress changes in accordance with pore pressure, the increasing pore pressure will not induce additional deformation or failure in the material, which is so called “neutral stress”. However, when it comes to the case of rock masses, the situation is different. Rock masses are naturally incised by joints and fissures, and the hydraulic conductivity is quite different for different rock materials. As pores and fissures are randomly distributed and connected, the increasing pore pressure would change the stress state and cause plastic deformation. It is the fundamental reason for the application of the effective stress law into yield criteria in the elasto-plastic models. For hydraulic structures, rock masses sustain the enormous weight of mountains and tectonic movements in natural conditions, and a wide range of geological materials are in the critical condition of yielding, especially the faults and joints. Therefore, the effective stress law explains accurately the phenomena of valley width contractions.

7 Conclusions

1) Valley contractions exist extensively and obviously accelerate during the impoundment process of hydraulic structures. The observed deformation of slopes during impoundment is irreversible. But the conventional analysis methods could hardly explain the phenomena.

2) The increasing of pore pressure results in the generalized effective stress beyond the yield criterion and leads to additional plastic deformation. Besides, it is reasonable that Biot coefficient is equal to 1 in practical numerical simulations.

3) The case of Jinping-I arch dam reveals that adopting effective stress law can precisely forecast the observed values of slope deformation, especially valley contractions. However, hydrostatic pressure on the dam surface is the key of dam body displacements during impoundment.

4) The slope deformation could thrust the dam body and worsen the stress state. It is indicated that the quantitative method is an effective and accurate one to assess the hazard of reservoir impoundment, and it is both a beneficial exploration and an improvement for hydraulic engineering design.

Acknowledge

The authors wish to express special thanks for the design data and monitoring values of Jinping-I and Ertan arch dam provided by PowerChina Chengdu Engineering Corporation Limited.

References

[1] GUDEHUS G. Finite elements in geomechanics [M]. London: John Wiley, 1977: 395–399.

[2] GUPTA H K. A review of recent studies of triggered earthquakes by artificial water reservoirs with special emphasis on earthquakes in Koyna, India [J]. Earth-Science Reviews, 2002, 58(3): 279–310.

[3] LADE P V, de BOER R. The concept of effective stress for soil, concrete and rock [J]. Geotechnique, 1997, 47(1): 61–78.

[4] de BUHAN P, DORMIEUX L. On the validity of the effective stress concept for assessing the strength of saturated porous materials: a homogenization approach [J]. Journal of the Mechanics and Physics of Solids, 1996, 44(10): 1649–1667.

[5] GENEVOIS R, GHIROTTI M. The 1963 vaiont landslide [J]. Giornale di Geologia Applicata, 2005, 1(1): 41–52.

[6] MLLER L. New considerations on the Vaiont slide [J]. Rock Mechanics & Engineering Geology, 1968, 6(1, 2): 4–91.

[7] TEZUKA M, KATAOKA K, SHIGEMITSU Y. Long-term behavior of Kurobe dam and its foundation rock [C]// Transactions of the International Congress on Large Dams. 2000, 3: 1337–1362.

[8] YANG Jie, HU De-xiu, GUAN Wen-hai. Analysis of high slope rock deformation and safety performance for left bank of Lijiaxia arch dam [J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(19): 3551–3560. (in Chinese)

[9] YANG Hong, TU Xiang-yang, XI Zhi-yong. Analysis on crack monitoring and control measures of Ertan high arch dam [J]. Pearl River, 2010, 31(6): 66–69. (in Chinese)

[10] YANG Hong, DONG Yan-jun. Analysis on monitoring data of Jinping-I hydropower dam during first impoundment [J]. Dam and Safety, 2015(3): 34–40. (in Chinese)

[11] ZHANG Chong, YIN Hua-an. Monitoring and back analysis of Xiluodu high arch dam during initial impoundment [J]. Design of Hydroelectric Power Station, 2014, 30(2): 7–12. (in Chinese)

[12] ZANGERL C, EBERHARDT E, PERZLMAIER S. Kinematic behaviour and velocity characteristics of a complex deep-seated crystalline rockslide system in relation to its interaction with a dam reservoir [J]. Engineering Geology, 2010, 112(1): 53–67.

[13] WANG J, XIANG W, LU N. Landsliding triggered by reservoir operation: A general conceptual model with a case study at Three Gorges Reservoir [J]. Acta Geotechnica, 2014, 9(5): 771–788.

[14] TERZAGHI K. Die berechnung der durchlassigkeitsziffer des tones aus dem verlauf der hydrodynamischen spannungserscheinungen [J]. Sitzungsberichte der Akademie der Wissenschaften in Wien, Mathematisch- Naturwissenschaftliche Klasse, Abteilung IIa, 1923, 132: 125–138. (in Germany)

[15] BIOT M A. Theory of elasticity and consolidation for a porous anisotropic solid [J]. Journal of Applied Physics, 1955, 26(2): 182–185.

[16] GEERTSMA J. The effect of fluid pressure decline on volumetric changes of porous rocks [J]. Petroleum Transactions, AIME, 1957, 210(3): 331–340.

[17] SKEMPTON A W. Effective stress in soils, concrete and rocks [C]// Selected papers on Soil Mechanics. London: Ice Publishing, 1984: 106–118.

[18] NUR A, BYERLEE J D. An exact effective stress law for elastic deformation of rock with fluids [J]. Journal of Geophysical Research, 1971, 76(26): 6414–6419.

[19] PRASAD M, MANGHNANI M H. Effects of pore and differential pressure on compressional wave velocity and quality factor in Berea and Michigan sandstones [J]. Geophysics, 1997, 62(4): 1163–1176.

[20] GARAT J, KRIEF M, STELLINGWERF J, et al. A petrophysical interpretation using the velocities of P and S waves (full-waveform sonic) [J]. The Log Analyst, 1990, 31(6): 355–369.

[21] SUKLJE L. Rheological aspects of soil mechanics [M]. London: Wiley-Interscience, 1969.

[22] CHEN Mian, CHEN Zhi-da. Effective stress laws for multi-porosity media [J]. Applied Mathematics and Mechanics, 1999, 20(11): 1121–1127.

[23] WALLS J, NUR A. Pore pressure and confining pressure dependence of permeability in sandstone [C]// Transactions of the 7th Formation Evaluation Symposium. Alberta, Calgary, 1979: 1–8.

[24] WALSH J B. Effect of pore pressure and confining pressure on fracture permeability [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, Pergamon, 1981, 18(5): 429–435.

[25] CHRISTENSEN N I, WANG H F. The influence of pore pressure and confining pressure on dynamic elastic properties of Berea sandstone [J]. Geophysics, 1985, 50(2): 207–213.

[26] BERNABE Y. The effective pressure law for permeability in Chelmsford granite and Barre granite [J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1986, 23(3): 267–275.

[27] ELLSWORTH W L. Injection-induced earthquakes [J]. Science, 2013, 341: 1225942.

[28] TERZAGHI K V. Simple tests determine hydrostatic uplift [J]. Engineering News Record, 1936, 116(25): 872–875.

[29] TIZDEL R R. Deformation of rock foundations of high dams after filling the reservoirs [J]. Hydrotechnical Construction, 1970, 4: 512–519.

[30] XIE S Y, SHAO J F. Elastoplastic deformation of a porous rock and water interaction [J]. International Journal of Plasticity, 2006, 22(12): 2195–2225.

[31] GURSON A L. Continuum theory of ductile rupture by void nucleation and growth: Part I—Yield criteria and flow rules for porous ductile media [J]. Journal of Engineering Materials and Technology, 1977, 99(1): 2–15.

[32] YANG Qiang, CHEN Xin, ZHOU Wei-yuan. A practical 3D elasto-plastic incremental method in FEM based on D-P yield criteria [J]. Chinese Journal of Geotechnical Engineering, 2002, 24(1): 16–20. (in Chinese)

[33] LIU Yao-ru, WU Zhe-shu, CHANG Qiang, et al. Stability and reinforcement analysis of rock slope based on elasto-plastic finite element method [J]. Journal of Central South University, 2015, 22: 2739–2751.

(Edited by FANG Jing-hua)

中文导读

岩体结构的有效应力原理及基于变形加固理论的水库蓄水分析

摘要：近年来，随着锦屏一级、溪洛渡等一批高坝大库开始蓄水运行，诱发的不可逆谷幅收缩等问题日益引起工程界的重视。但是，这些现象很难被经典的研究或设计方法解释，科学的理解蓄水过程中山体内水的影响是解释这些现象的基本。本文提出裂隙岩体有效应力原理，将其引入到基于Drucker-Prager准则的弹塑性模型并在三维非线性有限元程序TFINE中实现，发现蓄水过程中岩体的裂隙水压力增加是导致塑性变形是谷幅收缩的重要原因。通过在锦屏一级拱坝蓄水过程的谷幅变形分析验证了该方法的可靠性。

关键词：有效应力原理；弹塑性有限元；Biot系数；蓄水；谷幅收缩

Foundation item: Projects(51323014, 51479097, 51279086) supported by the National Natural Science Foundation of China; Project(2016-KY-2) supported by the State Key Laboratory of Hydroscience and Hydraulic Engineering, China

Received date: 2016-05-09; Accepted date: 2016-07-25

Corresponding author: LIU Yao-ru, Associate Professor, PhD; Tel: +86-10-62796954; E-mail: liuyaoru@tsinghua.edu.cn

Abstract: Reservoir impoundment is related to several hydraulic engineering concerns, including irreversible valley contractions, landslides and reservoir-induced earthquakes. However, these phenomena, such as valley contractions, are hardly to be explained by the conventional method. The scientific understanding of water effects during impoundment and their hazards to hydraulic structure are needed. The effective stress law for fissured rock masses is introduced in the elasto-plastic model employing the Drucker-Prager criterion and implemented in the three dimension (3D) nonlinear finite element method (FEM) program Three-dimensional FINite Element (TFINE). The slope deforms towards river-way during impoundment since the increasing pore pressure in fissures changes stress state and leads to additional plastic deformation in the rock materials. The value of Biot coefficient and the influence of water on rock materials are discussed in detail. Thus, the mechanism of slope deformation during the impoundment of Jinping-I arch dam is revealed, and the deformation is accurately measured. The application of the effective stress law provides a method to consider stress assessment, deformation evaluation and stability estimate of hydraulic structures during the impoundment process. This is a beneficial exploration and an improvement of hydraulic engineering design.