基于指数形式渗流下的软土一维非线性固结分析
李传勋1, 2,谢康和2,胡安峰2,刘兴旺3,王玉林2
(1. 江苏大学 土木工程与力学学院,江苏 镇江,212013;
2. 浙江大学 岩土工程研究所,浙江 杭州,310058;
3. 浙江省建筑设计研究院,浙江 杭州,310006)
摘 要:
资料表明软黏土中的渗流会遵循指数形式渗流定律,并且土体压缩性、渗透性在固结过程中会表现出明显的非线性特性。在土中自重应力沿深度均匀分布的假定下,推导建立基于指数形式渗流的软土一维非线性固结控制微分方程,并利用有限差分法对其进行数值求解。将数值解与达西渗流下Davis解析解进行对比,验证数值计算结果的可靠性。最后,对基于指数形式渗流下的一维非线性固结性状进行分析。研究结果表明:土层的固结速率在固结初期随渗流指数的增大而加快;而当时间因子超过某一值后,在固结后期固结速率随渗流指数的增加而变慢;土的压缩指数与渗透指数的比值越大,则土层的固结速率越慢;此外,土层中最终有效应力与初始有效应力的比值以及外荷载的等效水头与土层厚度的比值均对固结速率有较大影响。
关键词:
中图分类号:TU433 文献标志码:A 文章编号:1672-7207(2012)07-2789-07
Analysis of one-dimensional non-linear consolidation with exponential flow
LI Chuan-xun1, 2, XIE Kang-he2, HU An-feng2, LIU Xing-wang3, WANG Yu-lin2
(1. Faculty of Civil Engineering and mechanics, Jiangsu University, Zhenjiang 212013, China;
2. Institute of Geotechnical Engineering, Zhejiang University, Hangzhou 310058, China;
3. Zhejiang Province Institute of Architectural Design and Research, Hangzhou 310006, China)
Abstract: Experiments show that the water flow in soft soil may obey exponential flow law. Moreover, the soil exhibits an evident non-linearity in compressibility and permeability during the process of consolidation. By assuming a uniform distribution of initial self-weight stress, the differential equation governing one-dimensional non-linear consolidation was modified to consider exponential flow law, and numerical solutions were obtained by finite difference method. The reliability of numerical solutions was verified by comparing the numerical results with the analytical results obtained by Davis. Finally, one-dimensional non-linear consolidation behavior with exponential flow law was analyzed. The results show that the consolidation rate increases with the increase of the exponent at the early stage of consolidation, and decreases at the final stage of consolidation. The larger the ratio of compression index to permeability index, the slower the consolidation rate. In addition, both the ratio of the final effective stress to the initial one and the ratio of the equivalent water head of external loads to the thickness of a soil layer have great influences on the consolidation rate.
Key words: one-dimensional consolidation; exponential flow law; non-linear consolidation
土体的变形问题一直是岩土工程领域研究的重要内容,而固结理论又是解决土体变形问题的核心。因此,固结理论的研究一直是土力学研究的热点问题之一。目前的大多数固结理论中均假定土中渗流遵循达西定律,但是室内试验和现场观测均表明,土中渗流存在偏离达西定律的现象[1-6]。因此,对土中渗流遵循非达西渗流定律下的固结理论展开研究具有很重要的理论和实际意义。Hansbo[5-6]对非达西渗流下的一维固结和砂井固结进行分析,并且发现其实测沉降资料与非达西渗流下的计算结果相一致。谢海澜等[7]对非达西渗流下弱透水层的固结问题采用半解析方法进行计算,但是其计算过程中忽略了非达西渗流模式中的线性部分。刘忠玉等[8]、鄂健等[9]分别采用有限体积法和差分法对考虑非达西渗流的一维固结问题进行求解,并分析了非达西渗流对固结性状的影响。在以上考虑非达西渗流下的固结分析中,都假定在固结过程中土的渗透性和压缩性保持不变。但是,国内外研究均表明土体在固结过程中,其压缩性和渗透性无疑是会发生变化的[10-11]。刘忠玉等[12]对基于Hansbo渗流模式同时考虑了土体渗透、压缩性在固结过程中非线性变化的固结问题进行了分析。本文作者基于Slepicka[2]所提出的指数形式的非达西渗流定律,结合已有的室内固结渗透联合试验资料,考虑软土压缩、渗透性在固结过程中的非线性变化,对土体一维非线性固结展开研究,并分析不同参数下的固结性状。
1 室内固结渗透联合试验资料的整理
指数形式渗流定律可以表示为v=kvim,其中v为渗流速度,kv为渗透系数,m为渗流指数。当土中水力坡降较小时,渗流指数m>1;而当水力坡降较大时,渗流指数m<1;齐添[13]应用GDS高级固结仪对每级荷载下的土样进行多次的常水头渗透试验,结果表明萧山黏土中的渗流会出现了偏离达西定律的现象,并且指数形式渗流v=kvim与试验数据拟合最好。但没有总结渗流指数m和渗透系数kv随固结压力的变化情况。从文献[13]中表3.8可以看出:指数形式渗流定律的指数m在不同固结压力作用下基本保持不变,而渗透系数k则与固结压力之间在双对数坐标下呈线性关系,如图1所示。
众所周知,土体在固结过程中孔隙比与固结压力公认为在e~lg σ′坐标系中呈线性关系。因此,依lg kv~ lg σ′的线性关系,可以得到土的孔隙比与指数渗流规律的渗透系数在e~lg kv坐标系下呈线性关系。因此,已有的试验资料表明当土中渗流遵循指数形式的渗流规律时,随着固结压力的增加,一方面不同固结压力下指数形式渗流定律的指数大小基本保持不变,另一方面土的压缩系数和渗透系数均会随固结压力的不同而发生明显的变化,这种压缩、渗透性的非线性变化可以应用公式表示为
![]() (1)
(1)
![]() (2)
(2)
式中:![]() 为初始有效应力;
为初始有效应力;![]() 为竖向有效应力;e0为初始有效应力对应的初始孔隙比;kv0为渗透半对数曲线上相应于e0的渗透系数;cc和ck分别为压缩和渗透半对数曲线的斜率,称为压缩指数和渗透指数。
为竖向有效应力;e0为初始有效应力对应的初始孔隙比;kv0为渗透半对数曲线上相应于e0的渗透系数;cc和ck分别为压缩和渗透半对数曲线的斜率,称为压缩指数和渗透指数。

图1 土中指数渗流定律的渗透系数与固结压力关系曲线
Fig.1 Curve of permeability coefficient of exponential flow law versus consolidation pressure
2 控制微分方程及定解条件的建立
2.1 问题的描述及基本假定
图2所示为均质地基荷载边界情况及单元体示意图。厚度为H的均质地基,表面作用一瞬时施加的均布荷载q。地基表面透水,底面透水或不透水,土中渗流服从指数形式渗流定律。为了建立基于指数形式渗流下土体一维非线性固结控制方程,作如下基本假定:
(1) 饱和土中的固体颗粒和水均不可压缩。
(2) 土体仅产生竖向的小变形,且孔隙比与有效应力在半对数坐标系中为线性关系,如式(1)所示。
(3) 土中渗流仅发生在竖向,且遵循指数形式的渗流规律v=kvim。同时假定指数m在固结过程中保持不变,透系数kv与土体孔隙比的关系遵循式(2)所示的非线性变化。
(4) 假定均质地基中土体的自重应力不随着深度发生改变,即假定地基中初始有效应力为常数![]() 。
。

图2 均质地基荷载边界情况及单元体示意图
Fig.2 Loading, boundary conditions of soil layer and sketch of unit body
2.2 控制微分方程及其定解条件的建立
由式(1)和(2)可以得到:
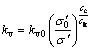 (3)
(3)
![]() (4)
(4)
其中:![]() 。
。
进而可以得到如下关系式:
 (5)
(5)
其中:![]() 。
。
从地基中取微元体,根据基本假定(1)可以得到流入和流出微元体的流量差等于微元体体积改变量这一连续条件,考虑土中指数形式的渗流定律,进而能够得到如下的控制微分方程:
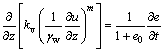 (6)
(6)
由方程(1)可以得到:
![]() (7)
(7)
将有效应力原理![]() 代入到方程(7)中,可以得到:
代入到方程(7)中,可以得到:
![]() (8)
(8)
将方程(8)代入到方程(6)中,可以得到瞬时加荷条件下基于指数形式渗流的一维非线性固结控制方程:
 (9)
(9)
其定解条件为:
u(0, t) = 0, t>0 (顶面排水); (10a)
![]() (底面不排水); (10b)
(底面不排水); (10b)
u(H, t)=0, t>0 (底面排水); (10c)
u(z, 0)= q。 (10d)
方程(9)为二阶非线性偏微分方程,很难获得其解析解,因此应用有限差分法对其进行数值求解。
3 微分方程的数值求解
3.1 控制方程的无量纲化
为了方便求得控制方程的数值解,定义如下无量纲变量:
![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() ;
;![]() 。
。
应用以上的无量纲变量,控制方程(9)转化为:
![]() (11)
(11)
定解条件((10a)~(10d))可以应用无量纲变量表示为:
U(0, Tv) = 0, Tv>0 (顶面排水); (12a)
![]() (底面不排水); (12b)
(底面不排水); (12b)
U(1, Tv)=0, Tv>0 (底面排水); (12c)
U(Z, 0)=b-1。 (12d)
3.2 孔隙水压力数值求解
首先,以h为空间步长从上至下将土层均匀离散为n个薄层,地基表面空间节点记为0,第j薄层底面处节点记为j,地基底面处节点记为n。与此同时,将时间域以变步长?Tvk进行离散,记第k个步长终止时刻Tvk=∑?Tvk。对于以上的非线性扩散方程,如果采用无条件稳定的Crank-Nicolson隐式差分格式[14],需要在每个时间增量内求解非线性方程组,这往往给求解过程带来麻烦。因此,本文采用拟线性扩散方程的隐式格式进行数值求解,具体差分方程可以表示为:
![]()
![]() (13)
(13)
式中:j=1, 2, …, n;k=0, 1, 2, …,![]() 表示空间节点j在Tvk时刻的超孔隙水压力无量纲值;
表示空间节点j在Tvk时刻的超孔隙水压力无量纲值;![]() ;
;
 (14)
(14)
 (15)
(15)
相应的定解条件可以应用离散点表示为:
![]() (顶面排水); (16a)
(顶面排水); (16a)
![]() (底面不排水); (16b)
(底面不排水); (16b)
![]() (底面排水); (16c)
(底面排水); (16c)
![]() 。 (16d)
。 (16d)
3.3 平均固结度的数值求解
通过对差分方程(13)进行求解,可以得到孔压的数值解答。之后,就可以对地基的平均固结度进行求解。由于考虑土体在固结过程中的非线性特性,故按变形定义的平均固结度和按孔压定义的平均固结度不再相等。
按孔压定义的平均固结度可以表示为:
 (17)
(17)
按变形定义的平均固结度可以表示为:

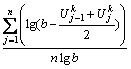 (18)
(18)
4 计算程序的验证
当指数形式渗流定律的指数等于1时,指数形式渗流定律退化为达西定律。Davis等[10]已经获得了在m=1及c=1条件下控制方程(9)的解析解。在单面排水条件下,差分计算的空间步长h=0.01,时间步长?Tv=0.000 001。将单面排水条件下的差分数值计算结果与相应的解析计算结果进行对比分析,如表1所示。
表1 差分计算结果与解析解对比
Table 1 Comparison of results by FDM with that by analytical method

从表1可以看出:解析计算结果与差分数值计算结果相比较,平均固结度的最大计算误差一般不超过0.01%,这在某种程度上也验证了所编制的差分计算程序的计算结果是可靠的。
5 不同参数下的固结性状分析
从以上求解过程可以看出:基于指数形式渗流的土体一维非线性固结的影响因素包括指数形式渗流中指数m、参数b,c以及qh。下面就单面排水条件下这些不同参数对固结性状的影响分别做出评价分析。
5.1 渗流指数m对固结性状的影响
Schmidt等[15]指出指数形式渗流定律中的指数在0.5~2.2之间变化,这也是本文分析指数对固结性状影响时所考虑的范围。根据文献[16]可以知道:基于指数形式渗流如果不考虑土体固结过程中的非线性变化,在较小的时间因子下地基的固结速率会随着渗流指数的增加而加快;而在较大的时间因子下,渗流指数越大,则地基的固结速率越慢。图3所示为不同渗流指数下考虑土体非线性固结特性的平均固结度与时间因子关系曲线。从图3可以看出:较小的时间因子下渗流指数越大,则地基的固结速率越快,并且m>1时的固结速率比达西渗流下的快;但是随着时间因子的增大,不同渗流指数下的固结曲线会相交于一 点,在该点处平均固结度不再随渗流指数的变化而变化;当时间因子超过该交点后,地基的固结速率随着渗流指数的增加而变慢。值得特别说明的是,不同渗流指数下固结曲线的交点所对应的时间因子会随着参数b,c及qh的变化而发生变化。这样固结性状原因在于固结的初始阶段,土层中的超孔隙水压力比较大,
平均水力坡降会大于1,此时![]() 这一项会随
这一项会随
着m的增大而逐渐增大,固结速率也就随着m的增大而变快;但是如果在固结的后期,此时地基土层中的
平均水力坡降会小于1,![]() 这一项会随着m
这一项会随着m
的增大而逐渐较小,此时土层的固结速率也会逐渐 减慢。
5.2 最终有效应力与初始有效应力比值b对固结性状的影响
如果参数b等于1,实际上意味着不再考虑土体的非线性固结特性,此时本文退化为文献[16]中的固结理论。图4给出了m=1.25,c分别等于0.5和1.5,参数b不同时按变形定义的平均固结度与时间因子的关系曲线。从图4可以看出:b越大,其固结曲线越偏离b=1时的固结曲线。即当c=0.5时,随着b的增加,固结速率会逐渐加快;而当c=1.5时,随着b的增加,土层的固结速率会逐渐减慢。这样的固结特性也说明,如果地基表面作用有与初始有效应力相比较大的外荷载时(此时b较大),如果不考虑土体在固结过程中的非线性固结特性,固结度的计算将会引起较大的误差。

图3 不同m时平均固结度与时间因子的关系
Fig.3 Curves of Us versus Tv with various m

图4 不同b时平均固结度与时间因子的关系
Fig.4 Curves of Us versus Tv with various b
5.3 压缩指数与渗透指数比值c对固结性状的影响
图5所示为在渗流指数m大于1时,不同c下土层按变形定义的平均固结度与时间因子之间的关系曲线。从图5可以发现:随着压缩指数与渗透指数比值的增加,土层的固结速率会逐渐减小。图6给出了当m小于1时,不同c下土层按孔压定义的平均固结度与时间因子之间的关系曲线。从图6同样能够发现:随着压缩指数与渗透指数比值c的增加,土层中孔隙水压力的消散速率会逐渐减小。因此,可以得到基于指数形式渗流定律的土层一维非线性固结,不管指数形式渗流的指数为何值(大于1、等于1或小于1),土层的固结速率都会随着压缩指数与渗透指数比值的增大而逐渐变缓。

图5 m=1.25时不同c时平均固结度和时间因子的关系
Fig.5 Curves of Us versus Tv with various c when m=1.25

图6 m=0.75时不同c时平均固结度和时间因子的关系
Fig.6 Curves of Us versus Tv with various c when m=0.75
5.4 初始有效应力的等效水头与土层厚度的比值qh对固结性状的影响
从以上的求解过程可以发现:如果指数形式渗流的指数等于1,即达西渗流下参数qh对固结性状是没有任何影响的。但是如果指数形式渗流的指数不等于1,则参数qh就会对固结速率产生一定的影响。图7给出了当渗流指数小于1即m=0.75时,参数qh对固结速率的影响。从图7可以看出:随着参数qh的增大,土层的固结速率会逐渐减小。容易知道,如果b保持不变,参数qh的增大就意味着外荷载的等效水头与土层厚度比值的增大。因此,在指数小于1的情况下,在参数b,c和m保持不变的条件下,外荷载的等效水头与土层厚度比值越大的土层,则在相同时间因子下对应土层的平均固结度越低。

图7 m=0.75时不同qh时平均固结度和时间因子的关系
Fig.7 Curves of Us versus Tv with various qh when m=0.75
图8所示为在渗流指数大于1即m=1.2时,参数qh对固结速率的影响。从图8可以看出:随着参数qh的增大,土层的固结速率也会逐渐增大。也就是说在参数b,c和m保持不变的条件下,外荷载的等效水头与土层厚度比值越大的土层,则在相同时间因子下对应土层的平均固结度越高。
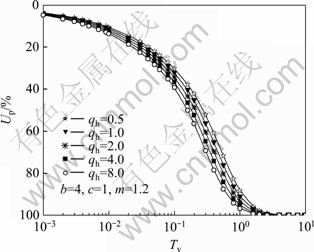
图8 m=1.25时不同qh时平均固结度和时间因子的关系
Fig.8 Curves of Us versus Tv with various qh when m=1.25
6 结论
(1) 在较小时间因子下,土层固结速率随着渗流指数的增大而加快;而当时间因子超过某一特定值后,土层固结速率随着渗流指数的增大而减慢。
(2) 土层中最终有效应力与初始有效应力的比值b对固结速率有较大影响。当c=0.5时,随着b的增加,固结速率会逐渐变快;而当c=1.5时,随着b的增加,固结速率逐渐减慢。
(3) 无论指数形式渗流定律的指数取何值,土体的压缩指数与渗透指数的比值均对固结速率有较大的影响。该比值越大,则土体的固结速率越慢。
(4) 作用于地基表面的外荷载的等效水头与土层厚度的比值对固结速率有一定影响。当土中的指数形式渗流的指数等于1时,该比值对固结速率没有影响;如果指数形式渗流的指数小于1,土层的固结速率随着该比值的增大而减慢;如果土中的指数形式渗流的指数大于1,土层的固结速率随着该比值的增大而加快。
参考文献:
[1] Hansbo S. Consolidation of clay with special reference to influence of vertical drains[C]//Swedish Geotechnical Institute Proceeding. Stockholm: Swedish Geotechnical Institute, 1960, 18: 45-50.
[2] Slepicka F. Contribution to the solution of the filtration law[C]// International Union of Geodesy and Geophysics, Commission of Subterranean Waters. Helsink, Finland, 1960: 245-258.
[3] 齐添, 谢康和, 胡安峰, 等. 萧山黏土非达西渗流性状的试验研究[J]. 浙江大学学报: 工学版, 2007, 41(6): 1023-1028.
QI Tian, XIE Kang-he, HU An-feng, et al. Laboratorial study on non-Darcy seepage in Xiaoshan clay[J]. Journal of Zhejiang University: Engineering Science, 2007, 41(6): 1023-1028.
[4] Dubin B, Moulin G. Influence of a critical gradient on the consolidation of clays[C]//Consolidation of soils: Testing and evaluation. West Conshohocken (PA): American Society for Testing and Materials, 1986: 354-377.
[5] Hansbo S. Aspects of vertical drain design: Darcian or non- Darcian flow[J]. Geotechnique, 1997, 47(5): 983-992.
[6] Hansbo S. Deviation from Darcy’s law observed in one- dimensional consolidation[J]. Geotechnique, 2003, 53(6): 601-605.
[7] 谢海澜, 武强, 赵增敏, 等. 考虑非达西流的弱透水层固结计算[J]. 岩土力学, 2007, 28(5): 1061-1065.
XIE Hai-lan, WU Qiang, ZHAO Zeng-min, et al. Consolidation computation of aquitard considering non-Darcy flow[J]. Rock and Soil Mechanics, 2007, 28(5): 1061-1065.
[8] 刘忠玉, 孙丽云, 乐金朝, 等. 基于非Darcy 渗流的饱和黏土一维固结理论[J]. 岩石力学与工程学报, 2009, 28(5): 973-979.
LIU Zhong-yu, SUN Li-yun, YUE Jin-chao, et al. One-dimensional consolidation theory of saturated clay based on non-Darcy flow[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 973-979.
[9] 鄂建, 陈刚, 孙爱荣. 考虑低速非Darcy 渗流的饱和黏性土一维固结分析[J]. 岩土工程学报, 2009, 31(7): 1115-1119.
E Jian, CHEN Gang, SUN Ai-rong. One-dimensional consolidation of saturated cohesive soil considering non-Darcy flows[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1115-1119.
[10] Davis E H, Raymond G P. A non-linear theory of consolidation[J]. Geotechnique, 1965, 15(2): 161-173.
[11] 李冰河, 谢康和, 应宏伟, 等. 初始有效应力沿深度变化的非线性一维固结半解析解[J]. 土木工程学报, 1999, 32(6): 47-52.
LI Bing-he, XIE Kang-he, YING Hong-wei, et al. Semi- analytical solution of 1D nonlinear consolidation considering the initial effective stress distribution[J]. China Civil Engineering Journal, 1999, 32(6): 47-52.
[12] 刘忠玉, 纠永志, 乐金朝, 等. 基于非Darcy渗流的饱和黏土一维非线性固结分析[J]. 岩石力学与工程学报, 2010, 29(11): 2348-2355.
LIU Zhong-yu, JIU Yong-zhi, YUE Jin-chao, et al. One- dimensional nonlinear consolidation analysis of saturated caly based on non-Darcy flow[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(11): 2348-2355.
[13] 齐添. 软土一维非线性固结理论与试验对比研究[D]. 杭州: 浙江大学岩土工程研究所, 2008: 55-58.
QI Tian. Theoretical and experimental studies on one- dimensional nonlinear consolidation of soft soil[D]. Hangzhou: Zhejiang University. Institute of Geotechnical Engineering, 2008: 55-58.
[14] 陆金甫, 关治. 偏微分方程数值解法[M]. 北京: 清华大学出版社, 2004: 171-178.
LU Jin-pu, GUAN Zhi. Numerical method for partial differential equation[M]. Beijing: Tsinghua University Press, 2004:171-178.
[15] Schmidt J D, Westmann R A. Consolidation of porous media with non-Darcy flow[J]. Journal of the Engineering Mechanics Division, 1973, EM6: 1201-1216.
[16] 李传勋, 谢康和, 卢萌盟, 等. 变荷载下基于指数形式渗流的一维固结分析[J]. 岩土力学, 2011, 32(2): 553-559.
LI Chuan-xun, XIE Kang-he, LU Meng-meng, et al. One- dimensional consolidation analysis considering exponential flow law and time-depending loading[J]. Rock and Soil Mechanics, 2011, 32(2): 553-559.
(编辑 陈爱华)
收稿日期:2011-09-12;修回日期:2011-12-19
基金项目:国家自然科学基金资助项目(50878191,51109092)
通信作者:谢康和(1956-),男,浙江建德人,教授,博士生导师,从事软黏土力学与地基处理方面研究;电话:0571-87951339;E-mail: zdkhxie@zju.edu.cn
摘要:已有的室内试验资料表明软黏土中的渗流会遵循指数形式渗流定律,并且土体压缩性、渗透性在固结过程中会表现出明显的非线性特性。在土中自重应力沿深度均匀分布的假定下,推导建立基于指数形式渗流的软土一维非线性固结控制微分方程,并利用有限差分法对其进行数值求解。将数值解与达西渗流下Davis解析解进行对比,验证数值计算结果的可靠性。最后,对基于指数形式渗流下的一维非线性固结性状进行分析。研究结果表明:土层的固结速率在固结初期随渗流指数的增大而加快;而当时间因子超过某一值后,在固结后期固结速率随渗流指数的增加而变慢;土的压缩指数与渗透指数的比值越大,则土层的固结速率越慢;此外,土层中最终有效应力与初始有效应力的比值以及外荷载的等效水头与土层厚度的比值均对固结速率有较大影响。


