J. Cent. South Univ. (2016) 23: 880-890
DOI: 10.1007/s11771-016-3135-8
Optimal multilevel thresholding based on molecular kinetic theory optimization algorithm and line intercept histogram
FAN Chao-dong(范朝冬)1, 2, REN Ke(任柯)1, 2, ZHANG Ying-jie(张英杰)3, YI Ling-zhi(易灵芝)1, 2
1. Key Laboratory of Intelligent Computing and Information Processing (Xiangtan University), Xiangtan 411105, China;
2. Hunan Province Cooperative Innovation Center for Wind Power Equipment and Energy Conversion,
Xiangtan 411101, China;
3. College of Information Science and Engineering, Hunan University, Changsha 410082, China
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
Among all segmentation techniques, Otsu thresholding method is widely used. Line intercept histogram based Otsu thresholding method (LIH Otsu method) can be more resistant to Gaussian noise, highly efficient in computing time, and can be easily extended to multilevel thresholding. But when images contain salt-and-pepper noise, LIH Otsu method performs poorly. An improved LIH Otsu method (ILIH Otsu method) is presented, which can be more resistant to Gaussian noise and salt-and-pepper noise. Moreover, it can be easily extended to multilevel thresholding. In order to improve the efficiency, the optimization algorithm based on the kinetic-molecular theory (KMTOA) is used to determine the optimal thresholds. The experimental results show that ILIH Otsu method has stronger anti-noise ability than two-dimensional Otsu thresholding method (2-D Otsu method), LIH Otsu method, K-means clustering algorithm and fuzzy clustering algorithm.
Key words:
1 Introduction
Image segmentation, the objective of which is to subdivide an image into several meaningful regions, is an important topic in image processing, computer vision and multimedia [1-2]. The reason for its importance is the dependency of the image analysis efficiency on image segmentation result. Over these years, many techniques have been developed for image segmentation [3-5]. Image segmentation can be traditionally classified into three categories: 1) threshold technique; 2) region-based image segmentation; 3) edge-based image segmentation [6]. Among all the existing segmentation techniques, the thresholding technique is one of the most popular techniques due to its simplicity, robustness, and accuracy [7]. The basic idea of automatic thresholding is to automatically select one or more optimal gray-level threshold values, for separating objects from the background based on their gray-level distribution. In earlier research, Otsu [8] proposed the maximum between-class variance criterion to select the best threshold, which is regarded as one of the classic techniques. The Otsu method has been proved to be one of the best thresholding techniques for its uniformity and shape measures [5].
However, in this segmentation method, only the gray level information of image pixels is taken into account, and even the space related information between them is underutilized. Thus, the efficiency of segmentation will degrade as the complexity increases and the signal-to-noise (SNR) degrades. For this reason, 2-D Otsu which employs the gray level information of each pixel and the spatial correlation information within its neighborhood has been proposed [9]. But 2-D Otsu also has some drawbacks as follows: 1) Due to the introduction of 2-D histogram, the complexity of computation has been increased and the operation time has been extended; 2) It is difficult to extend it to multilevel thresholding due to the complexity of the formulas; 3) The effect of segmentation is poor when images are corrupted by Gaussian noise. Line intercept histogram (LIH Otsu method) was proposed in Refs. [10-11]. LIH Otsu method can usually obtain better segmentation results than 2-D Otsu method when images are corrupted by Gaussian noise, and can be easily extended to multilevel thresholding. However, the effect of LIH Otsu method is substantially lowered when images are corrupted by salt-and-pepper noise.
This work first presents an improved LIH Otsu method (ILIH Otsu method), which employs a post-processing strategy to correct the noises. So, ILIH Otsu method has the advantages of LIH Otsu method, and performs better than LIH Otsu method when images are corrupted by salt-and-pepper noise. Images usually need to be divided into more than two groups, so we extended ILIH Otsu method to multilevel thresholding. However, inefficient formulation of between-class variance makes the method very time-consuming in multilevel threshold selection. To overcome this problem, many meta-heuristic algorithms, such as genetic algorithm (GA) [12], artificial bee colony algorithm (ABC) [13], particle swarm optimization algorithm (PSO) [14], were adopted to search for multilevel thresholds. But it is difficult for meta-heuristic algorithms to take into account the algorithm convergence and population diversity. In order to overcome this drawback, repulsion in physics was introduced to meta-heuristic algorithms and derived lots of improved algorithms, such as the molecular force based particle swarm optimization algorithm (MPSO) [15], later-stage repulsion-enhanced hybrid attraction and repulsion particle swarm optimization (LRPSO) [16], improved particle swarm optimization algorithm with reverse forecast and repulsion (RFRPSO) [17].
The repulsion based algorithms have achieved some improvements. But these algorithms still belong to the improved algorithms rather than new algorithms. In this regard, inspired by kinetic-molecular theory, we have proposed a new algorithm (kinetic-molecular theory based optimization algorithm, KMTOA) in Ref. [18]. Research shows that KMTOA has good performance in the robustness, solution quality, population diversity and convergence speed. So, in this work, we proposed a new optimal multilevel thresholding algorithm particularly suitable for multilevel image segmentation, which was based on KMTOA and ILIH Otsu method. Experimental results demonstrated the superiority of the new algorithm over other approaches such as LRPSO, RFRPSO, and MPSO.
2 Background and related work
In this section, two-dimensional Otsu thresholding method was introduced first. And then, its shortage of ignoring important information was analyzed, while ILIH Otsu method can overcome this drawback. So, ILIH Otsu method was expounded in the next.
2.1 Two-dimensional otsu thresholding method
It is supposed that the grey level of an image is from 1 to L. The abscissa represents gray level i and the ordinate represents the local average gray level j. Let nij be the frequency of (i, j), where f(x, y)=i, g(x, y)=j, and M×N denotes the image size, then
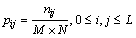(1)
where pij is a 2-D histogram of the image [11]. The 2-D histogram is a matrix of size L×L, which is shown in Fig. 1.
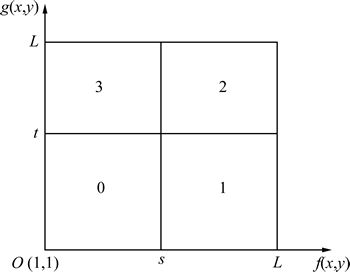
Fig. 1 2-D histogram
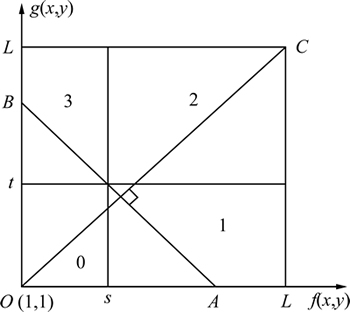
Fig. 2 Line intercept histogram
Let the threshold vector be (s, t), then divide 2-D histogram into four regions as shown in Fig. 1. These regions can be further classified into the diagonal regions 0 and 2 and off-diagonal regions 1 and 3, respectively. Regions 1 and 3 contain information about edges and noises alone, but they are ignored in the calculation in 2-D histogram thresholding methods, which use only two of the quadrants for segmentation, i.e., region 0 pixels as background and region 2 pixels as foreground [11].
Now suppose that the pixels are divided into two classes C0 and C1 (objects and background) by a threshold pair (s, t), then the probabilities of class occurrence are given by [19]
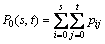(2)
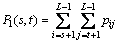(3)
And the corresponding class means levels are
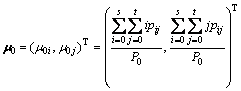
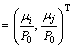(4)
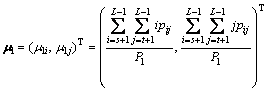(5)
The total mean level vector of the 2-D histogram is
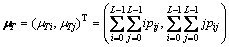(6)
The between-class variance matrix is defined as
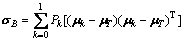(7)
By using the trace of sB as the measurement of between-class variance, there is
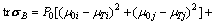
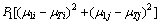(8)
Owing to the assumption that the occurrences of image data in off-diagonal regions of 2-D histogram can be neglected, then
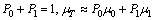(9)
By using Eq. (9), it can be obtained that
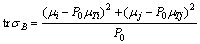(10)
A threshold vector (s*, t*) is selected by maximizing trsB
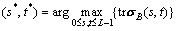(11)
2.2 Line intercept histogram based Otsu thresholding method
2-D Otsu thresholding method discards the pixels located in regions 1 and 3, which may ignore important information concerning the objects to be segmented. A thresholding line in the 2-D histogram plane was proposed to provide better segmentation in Ref. [20]. This method is costly, so some improved methods have been proposed to overcome the defects of being time-consuming [21-22]. Based on the ideal of thresholding line to divide the 2-D histogram, LIH Otsu method was proposed in Refs. [10-11].
As shown in Fig. 2, passing through (s, t), the line AB is defined to be the line perpendicular to the principal diagonal OC of the 2-D histogram, and has the intercept f(i, j). Then the image is segmented using line AB as the optimal thresholding line. Based on the straight line OC and the function f(i, j), line intercept histogram can be constructed as follows:
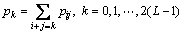(12)
Hence, the 2-D parameter space is reduced to a 1-D histogram of the variable. Obviously, each bin in this histogram will contain a contribution only from a unique line in the 2-D gray level histogram matrix. For image segmentation, the thresholding criterion can adopt that used in Otsu, i.e.
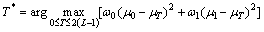(13)
where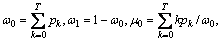 
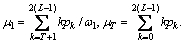
From above, we see that the regular 1-D criterion for Otsu is obtained. Hence, we can apply the regular Otsu on the line intercept histogram and find a threshold.
3 Proposed approach
3.1 Post-processing strategy
From Section 2.2, we know that LIH Otsu method can classify the pixels which have the same values of i+j into the same class. So, LIH Otsu method can be regarded as using Otsu after mean filtering. We know mean filtering is effective on Gaussian noise, but ineffective on salt-and-pepper noise. And LIH Otsu method considers the whole 2-D histogram (regions 0, 1, 2 and 3 in Fig. 2). When images are corrupted with salt-and-pepper noise, regions 1 and 3 contain information about noise. LIH Otsu method considers regions 1 and 3, but it is ineffective on salt-and-pepper noise. So, the LIH Otsu method may result in bad segments with salt-and-pepper noise.
From the analysis above, the reason why LIH Otsu method is ineffective on salt-and-pepper noise is that LIH Otsu method does not process the noise in regions 1 and 3. In order to eliminate this problem, post-processing strategy is applied after segmenting. The improved LIH Otsu method is referred to as ILIH Otsu method. Post-processing strategy uses neighborhoods of the pixel to decide which class the pixel belongs to.
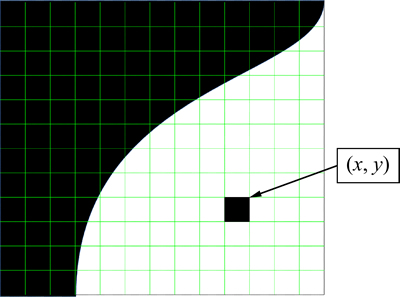
Fig. 3 All neighborhoods belonging to same class
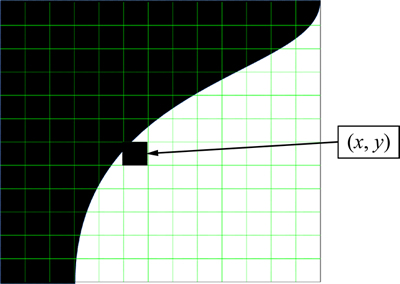
Fig. 4 Neighborhoods belonging to different class
Suppose that the current pixel is (x, y) and the size of the neighborhood window is 3×3. According to the difference of the neighborhood gray level, two kinds should be considered as follows: 1) All neighborhoods of (x, y) belong to the same class (object or background) as shown in Fig. 3. In this case, according to the connectivity of pixels, (x, y) should be divided into the same class. 2) As shown in Fig. 4, some neighborhoods belong to the same class, and the others belong to the other class. In this case, (x, y) may belong to the object or the background. We calculate the two kinds of neighborhoods. And we suppose that (x, y) belongs to the class which more neighborhoods belong to. Post-processing strategy always processes the noise in regions 1 and 3, as edges and noise always lie in regions 1 and 3.
3.2 Kinetic-molecular theory based optimization algorithm (KMTOA)
Real images usually contain more than one object. Hence, the problem of multilevel thresholding is regarded as an important area of research interest among the research communities worldwide. The Otsu method can be easily extended to multilevel thresholding problem, but inefficient in determining the optimal thresholds due to the exponential growth in computation time. To overcome this problem, we apply a new intelligent optimization algorithm which we called kinetic-molecular theory based optimization algorithm (KMTOA) to search for the multilevel thresholds using ILIH Otsu method. This proposed method is called KMTOA based ILIH Otsu-method (KMTOA_ILIH Otsu method).
KMTOA is motivated by kinetic-molecular theory. In KMTOA, potential solutions can be regarded as molecules moving around in a space. Each molecule moves in the search space towards the optimal solution based on the molecular force between this molecule and the global best molecule. The main content of KMTOA includes attraction, repulsion and thermal motion.
Attraction: According to the kinetic-molecular theory, a molecule is attracted by the other when r>r0. Here, r represents the distance between the two molecules, and r0 is called the balance position. In order to ensure that molecules converge towards the optimal one, KMTOA assumes that only the optimal molecule could generate force to attract the others. Let rand represent a uniform random variable in the interval [0,1], and Pattraction which is a threshold in the interval [0,1] represent the probability of this molecule attracted by the optimal molecule. The attraction of molecule i could be calculated by
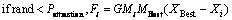(14)
where Fi represents the attraction exerted on molecule i; XBest and Xi are the positions of the optimal molecule and molecule i respectively; G is a gravitational constant; MBest and Mi are the masses related to the optimal molecule and molecule i, respectively.
Repulsion: Maintain that the diversity of population is crucial to improve the performance of the swarm intelligence algorithm. Enlightened by the repulsion between molecules, KMTOA uses repulsion to maintain the diversity of population. Similar with attraction, KMTOA assumes that only the optimal molecule could generate repulsive force to repel the others. Let Prepulsion which is a threshold in the interval [0, 1] represent the probability of this molecule repelled by the optimal molecule. The formula of repulsive force is as follows:
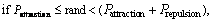
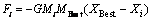(15)
where Fi, XBest, Xi, G, MBest and Mi are definded as above.
By the laws of motion, the acceleration of the molecule i was given as follows:
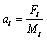(16)
Thermal motion: If we only used attraction and repulsion as above, it is possible that all molecules converge to the current optimal molecule. In this case, the algorithm will be trapped by the current optimal molecule, and cannot jump from it. In order to maintain the search capability of KMTOA, making an analogy to molecular thermal motion, a method was proposed here. Similarly, KMTOA uses Pmotion (Pattraction+Prepulsion+ Pmotion=1) which is a threshold in the interval [0, 1] to decide whether or not the molecule dose perform thermal motion. Inspired by Gauss mutation [23], when (Pattraction+Prepulsion)≤r and <(Pattraction+Prepulsion+Pmotion) (or (Pattraction+Prepulsion)≤r and<1), the acceleration of molecule i is as follows:
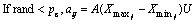(17)
where aij is the jth component of ai; pc is the mutation rate;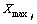 
and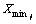 
are the upper and lower bounds of the jth component of solution space respectively; U is a normally distributed stochastic variable; and A represents the amplitude calculated by (1-0.9t/T).
Elitism strategy: Through the operations above, the optimal molecule may degenerate. In Ref. [24], elitism strategy was applied to avoid losing the current optimal individual. So, KMTOA applies elitism strategy after each iteration. Details of the elitism strategy in KMTOA can be described as follows: Assume that XKBest(t) is the optimal molecule in the current population at generation t, and f (XKBest(t)) represents the objective function value of XKBest(t). That is f(XKBest(t))=min(f(Xj(t))) (j∈{1, 2, …, Size}, and Size represents the population size). At generation t+1, let f(XKBest(t+1))=min(f(Xj(t+1))). If f(XKBest(t+1))>f(XKBest(t)), it means that the optimal molecule has degenerated. At this moment, let XKBest(t+1)=XKBest(t).
3.3 Application of KMTOA for multilevel thresholding problem
This work presents a quick solution to the multilevel image thresholding problems using the KMTOA. The number of threshold levels is the dimension of the problem. For example, if there are ‘m’ threshold levels, the ith molecule is represented as follows:
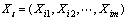
The procedure of the proposed multilevel thresholding method is as follows:
Step 1: Initialize the swarm and parameters. For a population size N, the molecules are randomly generated between the minimum and the maximum limits of the threshold values.
Step 2: The objective function value of all solutions Xi is evaluated. According to eq. (13), ILIH Otsu method is extended to multilevel thresholding, and the optimal thresholds are chosen by maximizing the following equation:
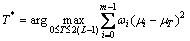(18)
where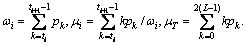 
KMTOA searches the space based on the minimum of the objective function values. So, we choose the optimal thresholds by minimizing the following equation:
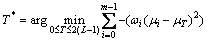(19)
Step 3: For every molecule, determine that its resultant is attraction, repulsion or zero. Compute the force between the molecule and the current optimal molecule by Eqs. (14) or (15). And compute its acceleration by Eq. (16).
Step 4: Evaluate the velocity and update the swarm. The velocity and position can be calculated as
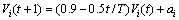(20)
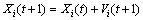(21)
Step 5: After updating the swarm, elitism strategy is carried out.
Step 6: Stopping criteria: If the stopping criteria are met, the position of the optimal molecule is the optimal threshold value. Otherwise, the procedure is repeated from step 2. The run of the algorithm is stopped when the cycle is equal to the maximum iteration number or the fitness values of the best solution reach the optimal values of the objective function obtained by exhaustive search method.
4 Results and discussions
In order to test the efficiency of KMTOA_ILIH Otsu method, two aspects including the segmentation effect under noisy situation and calculation efficiency are taken into consideration. In order to compare these performances, three experiments were carried out. In experiment 1, we compared KMTOA_ILIH Otsu with other Otsu methods. In experiment 2, we compared KMTOA_ILIH Otsu with clustering algorithms for segmentation such as K-means clustering algorithm and fuzzy clustering algorithm. And we compared KMTOA_ILIH Otsu with other population-based thresholding algorithms in experiment 3. All experiments were implemented in matlab 7.9 and executed on Window XP with 2.7 GHz CPU, 2GB RAM. House consisting of 256×256 pixels and Man consisting of 1024×1024 pixels are provided by the USC-SIPI Image Database [25]. In order to test the segmentation effect under noisy situation, we added noise to House and Man, and use the images corrupted with noise as test images. Figure 5 depicts the test images corrupted with different kinds of noise.
4.1 Comparison with other Otsu methods
Because 2-D Otsu method is difficult to be extended to multilevel thresholding, we first compare KMTOA_ILIH Otsu method with 2-D Otsu method and LIH Otsu method under bi-level thresholding. The segmented images by 2-D Otsu method, LIH Otsu method and KMTOA_ILIH Otsu method are shown in Figs. 6-8, respectively. From Fig. 6, we know that 2-D Otsu method discarded the pixels located in regions 1 and 3, which ignored some important information. So, the outline of the object is not clear. Figure 7 shows that LIH Otsu method is effective when images only contain Gaussian noise, but it is so bad when images contain only salt-and-pepper noise. It can be seen clearly that KMTOA_ILIH Otsu method can outperform 2-D Otsu method and LIH Otsu method in segmenting images with different noises.
Fig. 5 Images corrupted with noises:
Fig. 6 Segmentation results of images by 2-D Otsu method: (a, d) Salt-and-pepper noise; (b, e) Gaussian noise; (c, f) Mixed Gaussian and salt-and-pepper noise
Fig. 7 Segmentation results of images by LIH Otsu method:
Fig. 8 Segmentation results of images by KMTOA_ILIH Otsu method:
4.2 Compared with clustering algorithms for segmentation
In experiment 1, we have compared KMTOA_ILIH Otsu method with other Otsu methods to testify the efficiency of the improvements. In order to compare KMTOA_ILIH Otsu method with other techniques for image segmentation, in experiment two, we compared it with clustering methods such as K-means clustering algorithm and fuzzy clustering algorithm. The number of thresholds was set to be 3 and the number of clusters was 4. The segmented images by K-means clustering algorithm, fuzzy clustering algorithm and KMTOA_ILIH Otsu method are shown in Figs. 9-11, respectively.
Figure 9 shows that many pixels are wrongly segmented. Some pixels which belong to object were divided into background, and some pixels which belong to background were divided into objects. From Fig. 10, we know that fuzzy clustering algorithm segmented the images more precisely than K-means clustering algorithm. From Figs. 9 and 10, we can clearly see that the segmentation results using K-means clustering algorithm and fuzzy clustering algorithm are affected greatly by noise, while the results by KMTOA_ILIH Otsu method are much better, as shown in Fig. 11.
4.3 Comparison of KMTOA with other optimization algorithms
LRPSO and RFRPSO are repulsion based optimization algorithm, and have good performance in optimization. So, in this section, we evaluated the performance on the multilevel thresholding methods based on KMTOA, LRPSO and RFRPSO. The exhaustive search method was also conducted for deriving the optimal solution for comparison. We used the optimal values obtained by exhaustive search method in conjunction with the maximum iteration number as stopping criterion. The run of each algorithm was stopped when the cycle was equal to the maximum iteration number or the fitness values of the best solution reached the optimal values obtained by exhaustive search method (i.e. |f(T*)-fop|≤ε=10-9, where fop was the optimal value obtained by exhaustive search method and ε was a threshold value which fixed the accuracy of the measurement.). The images shown in Fig. 5 were taken as the test images.
Fig. 9 Segmentation results of images by K-means clustering algorithm:
Fig. 10 Segmentation results of images by fuzzy clustering algorithm:
Fig. 11 Segmentation results of images by KMTOA_ILIH Otsu method:
Table 1 Mean values of optimal fitness values over 50 runs
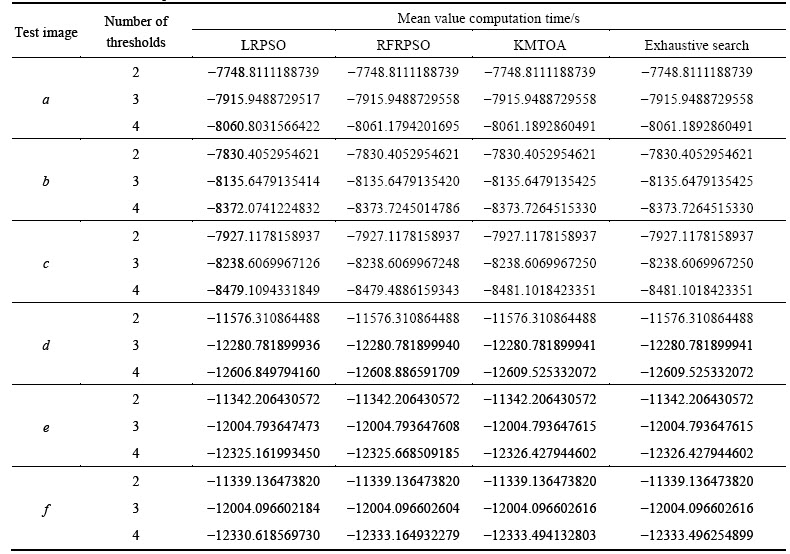
In order to compare the quality of the solutions provided by various methods, the value of the best fitness f(T*) corresponding with the best threshold solution T* was used as comparative criterion. Of course, the smaller the objective function value, the better the algorithm. Table 1 shows the mean values of the optimal fitness values derived by various methods. From the results shown in Table 1, compared with the other population-based algorithms, KMTOA gets the optimal fitness values equal to or nearest those provided by the exhaustive search method.
Due to the randomness of the evolutionary algorithms, their performance cannot be judged by the result of a single run. Many numbers of trials with different initializations should be made to reach valid conclusions about the performance of the algorithms. The stability of KMTOA and other algorithm were examined based on the standard deviation. The standard deviation is represented as follows [7, 26].
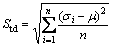(22)
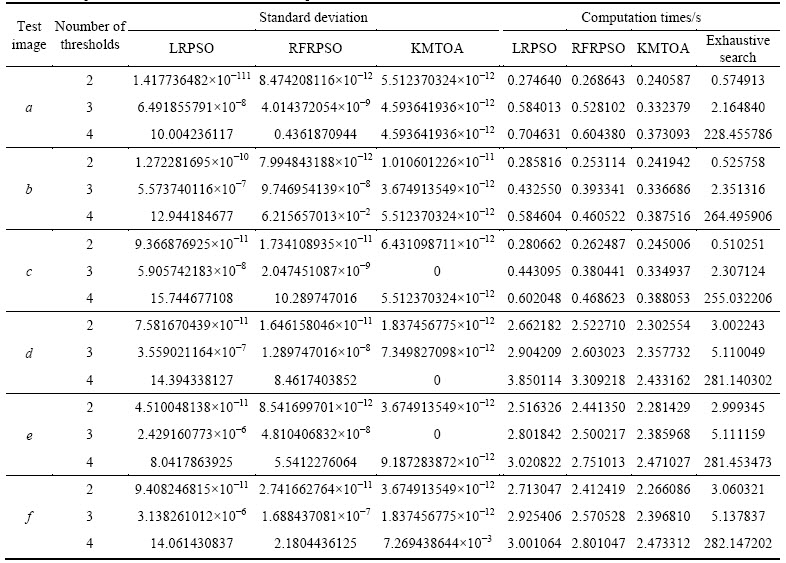
where std is the standard deviation; si is the best objective value of the ith run of the algorithm; μ is the average value of s; and n is the number of runs for each algorithm (n=50). The standard deviation values and computation time obtained by the various algorithms are given in Table 2. The higher standard deviation shows that the results of the experiment are more unstable. From Table 2, it is seen that KMTOA is more stable than other algorithms for each test images. Furthermore, we find that the computation time of exhaustive search method grows exponentially with the number of required thresholds, and KMTOA converges more quickly than other algorithms. These results can explain why we select KMTOA to search the optimal thresholds.
Table 2 Comparison of standard deviation and computation times for various methods
5 Conclusions
1) LIH Otsu method is effective on Gaussian noise, but ineffective on salt-and-pepper noise. So, an improved LIH Otsu method, which used post-processing strategy to the segmented images, was proposed here. Based on post-processing strategy, ILIH Otsu method can be more resistant to Gaussian noise and salt-and-pepper noise. From the evaluation of the resulted images, we conclude that the proposed thresholding methods obtain better results than those obtained by other widely used variance-based methods, i.e., 2-D Otsu method and LIH Otsu method.
2) Based on attraction-repulsion mechanism, KMTOA can take into account both population diversity and convergence speed. In view of the excellent performance of KMTOA, combining ILIH Otsu method, a new multilevel thresholding method (named KMTOA_ILIH Otsu method) was proposed and its detailed steps were explained. From the comparison results of KMTOA_ILIH Otsu method, K-means clustering algorithm and fuzzy clustering algorithm, we know that KMTOA_ILIH Otsu method gives satisfactory results, and it is robust against noise.
3) In order to verify the effectiveness of KMTOA_ILIH Otsu method, KMTOA has been compared with LRPSO and RFRPSO, and it is found that KMTOA outperforms LRPSO and RFRPSO in terms of solution quality, robustness and computation time. In summary, KMTOA_ILIH Otsu method is an efficient tool for image segmentation. In the future, we shall explore how to extend our approach to segment more complex images in different application areas.
References
[1] MAITRA M, CHATTERJEE A. A novel technique for multilevel optimal magnetic resonance brain image thresholding using bacterial foraging [J]. Measurement, 2008, 41(10): 1124-1134.
[2] YU Zhi-wen, WANG Hua-san, WEN Gui-hua. A modified support vector machine and its application to image segmentation [J]. Image and Vision Computing, 2011, 29(1): 29-40.
[3] HARALICK R M, SHAPIRO L G. Image segmentation techniques [J]. Computer Vision, Graphics, and Image Processing, 1985, 29(1): 100-132.
[4] SAHOO P K, SOLTANI S, WONG A K C. A survey of thresholding techniques [J]. Computer, Vision, Graphics and Image Processing, 1988, 41(2): 233-260.
[5] SEZGIN M, SANKUR B. Survey over image thresholding techniques and quantitative performance evaluation [J]. Journal of Electronic Imaging, 2004, 13(1): 146-168.
[6] KUMAR S, PANT M, RAY A. Differential evolution embedded Otsu’s method for optimized image thresholding [C]// IEEE Conf Information and Communication Technologies. Mumbai: IEEE, 2011: 325-329.
[7] GAO Hao, XU Wen-bo, SUN Jun, TANG Yu-lan. Multilevel thresholding for image segmentation through an improved quantum-behaved particle swarm algorithm [J]. IEEE Transactions on Instrumentation and Measurement, 2010, 59(4): 934-946.
[8] OTSU N. A threshold selection method from gray-level histograms [J]. IEEE Transactions on Systems, Man and Cybernetics, 1979, SMC-9(1): 62-66.
[9] LIU Jian-zhuang, LI Wen-qing. The automatic thresholding of gray-level pictures via twodimensional Otsu method [J]. Acta Automatica Sinica, 1993, 19(1): 101-105. (in Chinese)
[10] HE Zhi-yong, SUN Li-ning, HUANG Wei-guo, CHEN Li-guo. Thresholding segmentation algorithm based on Otsu criterion and line intercept histogram [J]. Optics and Precision Engineering, 2012, 20(10): 2315-2323. (in Chinese)
[11] NIE Fang-yan, WANG Yong-lin, PAN Mei-sen, PENG Guang-hua, ZHANG Ping-feng. Two-dimensional extension of variance-based thresholding for image segmentation [J]. Multidimensional System and Signal Processing, 2013, 24(3): 485-501.
[12] YIN Peng-yeng, CHEN Ling-hwei. A fast iterative scheme for multilevel thresholding methods [J]. Signal Process, 1997, 60(3): 305-313.
[13] HORNG M H. Multilevel thresholding selection based on the artificial bee colony algorithm for image segmentation [J]. Expert Systems with Applications. 2011, 38(11): 13785-13791.
[14] CHANDER A, CHATTERJEE A, SIARRY P. A new social and momentum component adaptive PSO algorithm for image segmentation [J]. Expert Systems with Applications, 2011, 38(5): 4998-5004.
[15] XU Xing, LI Yuang-xiang, JIANG Da-zhi, TANG Ming-duan, FANG Shen-lin. Improved particle swarm optimization algorithm based on theory of molecular motion [J]. Journal of System Simulation, 2009, 21(7): 1904-1907. (in Chinese)
[16] CHEN Dong-ning, YAO Cheng-yu, WANG Bin, ZHANG Rui-xing. LRPSO algorithm and applications in reliability optimization [J]. China Mechanical Engineering, 2014, 25(21): 2930-2936. (in Chinese)
[17] FAN Cheng-li, XING Qing-hua, LI Xiang, WANG Zhen-jiang. Improved particle swarm optimization algorithm with reverse forecast and repulsion [J]. Control and Decision, 2015, 30(2): 311-315. (in Chinese)
[18] FAN Chao-dong, OUYANG Hong-lin, ZHANG Ying-jie, AI Zhao-yang. Optimization algorithm based on kinetic-molecular theory [J]. Journal of Central South University, 2013, 20(12): 3504-3512.
[19] ZHANG Jun, HU Jing-lu. Image segmentation based on 2D Otsu method with histogram analysis [C]// IEEE Conf Computer Science and Software Engineering. Washington DC: IEEE Computer Society, 2008: 105-108.
[20] SAHOO P K, SLAAF D W, ALBERT T A. Threshold selection using a minimal histogram entropy difference [J]. Optical Engineering, 1997, 36(7): 1976-1981.
[21] FAN Jiu-lun, ZHAO Feng. Two-dimensional Otsu’s curve thresholding segmentation method for gray-level images [J]. Acta Electronica Sinica, 2007, 35(4): 751-755. (in Chinese)
[22] WU Yi-quan, PAN Zhe, WU Wen-yi. Image thresholding based on two-dimensional histogram oblique segmentation and its fast recurring algorithm [J]. Journal on Communication. 2008, 29(4): 77-83. (in Chinese)
[23] HAN Xu-ming, ZUO Wang-li, WANG Li-min, SHI Xiao-hu. Atmospheric quality assessment model based on immune algorithm optimization and its applications [J]. Journal of Computer Research and Development, 2011, 48(7): 1307-1313. (in Chinese)
[24] DEB K, PRATAP A, AGARWAL S, MCYARIVAN T. A fast and elitist multiobjective genetic algorithm: NSGA-II [J]. IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182-197.
[25] USC-SIPI Image Database. [Online] [2014]. http://sipi.usc.edu/ database/database.php.
[26] GHAMISI P, COUCEIRO M S, BENEDIKTSSON J A, FERREIRA N F. An efficient method for segmentation of images based on fractional calculus and natural selection [J]. Expert Systems with Applications, 2012, 39(16): 12407-12417.
(Edited by YANG Hua)
Foundation item: Project(61440026) supported by the National Natural Science Foundation of China; Project(11KZ|KZ08062) supported by Doctoral research project of Xiangtan University, China
Received date: 2015-01-21; Accepted date: 2015-07-22
Corresponding author: YI Ling-zhi, Professor; Tel: +86-731-58292224; E-mail: 450337856@qq.com
Abstract: Among all segmentation techniques, Otsu thresholding method is widely used. Line intercept histogram based Otsu thresholding method (LIH Otsu method) can be more resistant to Gaussian noise, highly efficient in computing time, and can be easily extended to multilevel thresholding. But when images contain salt-and-pepper noise, LIH Otsu method performs poorly. An improved LIH Otsu method (ILIH Otsu method) is presented, which can be more resistant to Gaussian noise and salt-and-pepper noise. Moreover, it can be easily extended to multilevel thresholding. In order to improve the efficiency, the optimization algorithm based on the kinetic-molecular theory (KMTOA) is used to determine the optimal thresholds. The experimental results show that ILIH Otsu method has stronger anti-noise ability than two-dimensional Otsu thresholding method (2-D Otsu method), LIH Otsu method, K-means clustering algorithm and fuzzy clustering algorithm.
