
Numerical modeling and deformation analysis for electromagnetically assisted deep drawing of AA5052 sheet
LIU Da-hai(刘大海), LI Chun-feng(李春峰), YU Hai-ping(于海平)
School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
Received 26 September 2008; accepted 8 January 2009
Abstract:
Electromagnetic forming(EMF) is a high-velocity manufacturing technique which uses electromagnetic (Lorentz) body forces to shape sheet metal parts. One of the several advantages of EMF is the considerable ductility increase observed in several metals, with aluminum featuring prominently among them. Electromagnetically assisted sheet metal stamping(EMAS) is an innovative hybrid sheet metal processing technique that combines EMF into traditional stamping. To evaluate the efficiency of this technique, an experimental scheme of EMAS was established according to the conventional stamping of cylindrical parts from aluminum and the formability encountered was discussed. Furthermore, a “multi-step, loose coupling” numerical scheme was proposed to investigate the deformation behaviors based on the ANSYS Multiphysics/LS-DYNA platform through establishing user-defined subroutines. The results show that electromagnetically assisted deep drawing can remarkably improve the formability of aluminum cylindrical parts. The proposed numerical scheme can successfully simulate the related Stamping-EMF process, and the deformation characteristics of sheet metal reflect experimental results. The predicted results are also validated with the profiles of the deformed sheets in experiments.
Key words:
aluminum alloy; electromagnetic forming(EMF); electromagnetically assisted sheet metal stamping(EMAS); coupling analysis;
1 Introduction
In recent years, the lightweight trend of materials and structures has led to increasing usage of such structural materials as aluminum alloys in automotive and aeronautic industries[1]. However, the poor formability of aluminum as a counterpart of steel has restricted its wide applications in traditional press forming of complex parts. Consequently, researchers have devoted to developing new processing techniques or exploring the traditional means to improve the formability of aluminum alloys[2].
In order to solve the formability problems of aluminum in shaping complicated shell parts, a new technique, electromagnetically assisted sheet metal stamping(EMAS) has been developed, which is a hybrid method integrating traditional stamping with electromagnetic forming(EMF). EMAS, firstly referred to as the matched tool-electromagnetic(MT-EM) process [3-5], combines the advantages of high-velocity EMF on forming aluminum alloys into the traditional sheet metal stamping process. And in principle, both operations can be carried out in one nearly-traditional press stroke[3]. This approach has been demonstrated in a limited way in cooperation with the USAMP materials by VOHNOUT et al[4]. The project examined how an EMF operation combined with a softened initial shape could enable the fabrication of one-piece aluminum door inner. A pre-forming with softened corners was fabricated firstly, and then it was electromagnetically re-formed into a GM Cavalier door inner die. The electromagnetic operation took the corner back to its design radius[3-4]. Plane strain values in excess of 25% were observed on the electromagnetically reformed panel, which are larger than those in conventional stamping[4-5]. Despite the separate operations for EMAS process, this experiment is significant since it proves the feasibility of the incorporation of electromagnetic coils with the conventional stamping tools. The localization inherent in the hybrid MT-EM process keeps the total EMF energy requirements within manageable levels. Furthermore, a lower energy variation of the MT-EM process was developed by SHANG[6] based on the idea of incremental forming, in which the EMF event does not perform the final forming of a local geometry but applies appropriate small electromagnetic pulses to the strategically chosen regions of the metal sheet in order to control the strain distribution while the tool punch is advancing. A series of experiments conducted by SHANG[6] on aluminum alloys have shown that EMAS could greatly increase the formability of sheet metal stamping and have also verified that EMF coils can be fabricated into a wide variety of configurations and used in conjunction with stamping operations. All these try-outs mentioned above have consolidated the basis of EMAS in principle and have been paid extensive attentions by researchers.
Nevertheless, although many experimental investigations have been performed on the technical aspects of EMAS till now, this technique is still in laboratory, and the forming theory or basis, especially deformation mechanism has been little discussed. In the present work, to get a good understanding of the deformation mechanism of EMAS, its technology basis was discussed and investigated. Considering that EMAS is a process combined with multi-physics environments, and concerns both quasi-static process and high-speed dynamic process, which is impossible to be fully understood by using analytic and experimental methods, or typical numerical method, we attempted to establish a new numerical scheme that can reasonably reflect the coupled multi-physics environments and the complex loadings in EMAS. Further, based on this FEM model, the deformation process of a specified electro- magnetically assisted deep drawing of 5052-O aluminum alloy was analyzed and its deformation behaviors were investigated and verified.
2 Principle of EMAS
Fig.1 shows the typical EMAS process[4]. It is a hybrid processing technique for complicated parts, which is conducted in a nearly-traditional press stroke by using tool sets embedded with EMF coils. Generally, the stamping parts are large and need very large electromagnetic energy input if using high velocity forming of EMF to form the whole metal parts alone. Due to the practical limits of strength of tooling materials and the capacity of capacitor bank, the electromagnetic forces cannot be made arbitrarily large to form large parts. To reduce the requirements of the robust tooling and the large capacitor bank, the high power pulses will be applied only in the final forming and only at the local areas of the part where required. And most of the parts will still be formed by conventional stamping. This is the key idea of the typical EMAS process[5-6]. The essential attributions of the hybrid process are that the majority of the forming is done conventionally, with the EMF process only applied locally to difficult geometry regions of the part. The difficult areas are washed out of the conventional forming tool and then added back by the EMF method. Optimally the EMF process takes place within the primary press forming cycle but can be considered a secondary operation.
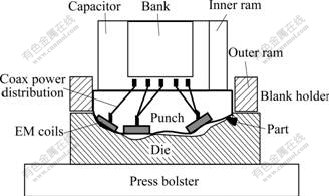
Fig.1 Schematic of typical EMAS process[4]
3 Electromagnetically assisted deep drawing
To assess the material response and deformation behavior, a reasonable and effective EMAS scheme should be firstly established, meanwhile, this also provides a specific implementation example for FEM modeling. In this work, it is much more representative of establishing an EMAS process on the basis of deep drawing process for reasons that on one hand, there exist some restrictions on forming deep shells by using EMF alone[4], which is the primary motivation why an EMF operation should be combined with a conventional stamping process, and that on the other hand, deep drawing is a typical sheet metal stamping process. As a result, the specified simple cylindrical deep drawing of 5052-O aluminum alloy is chosen, based on which the EMAS scheme is established and is referred to as electromagnetically assisted deep drawing here.
3.1 Problem descriptions
As we know, tearing at the bottom corner is a basic formability problem in traditional cylindrical deep drawing. Thus, shaping a cylindrical part with a much smaller bottom corner radius, the multi-step deep drawing performance or some other special forming techniques should be involved with. That is even true for a part deformed by such low formability alloys as aluminum. Aiming at the tearing problem at the bottom corner region in cylindrical deep drawing process, a Stamping (deep drawing)-EMF scheme (namely a typical EMAS) was established as follows. Firstly, we specified the problem by conducting a series of conventional formability experiments on 1 mm-thick 5052-O aluminum alloy sheets with the setup shown in Fig.2, and designed according to the standard Swift cup test. Fig.3 shows the distribution of the limited drawing depth using two kinds of punches with radii rp of 5 mm and 8 mm, respectively. As can be seen, with a drawing depth of 24.5 mm, statistically, a 5 mm-radius punch cannot deform a cup without tearing at the bottom corner while an 8 mm-radius punch works. Then, based on the idea whether the EMAS process can successfully form an aluminum cup with a bottom corner radius similar or much smaller than that could theoretically deformed by a 5 mm-radius punch, we established an electro- magnetically assisted deep drawing scheme as shown in Fig.4. The cup was formed close to the desired shape with the conventional deep drawing firstly. Then a secondary electromagnetic operation was carried out to form the sharp bottom corner by the designed coils embedded in the tool halves. The main dimension parameters are the same with those in conventional tools sets shown in Fig.2. The designed parameters according to the formability experiments as mentioned are the punch radius (rp) of 8 mm for pre-form stage, the forming depth (Hm) of 24.5 mm and die bottom corner radius (rb) for the final stage of 5 mm and 3 mm, respectively.
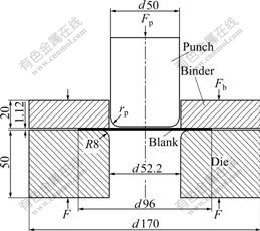
Fig.2 Conventional axisymmetric deep drawing
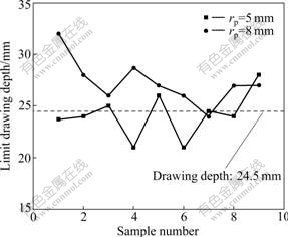
Fig.3 Distributions of limited drawing depth with different punch radii
3.2 Formability validation
To assess the efficiency of the proposed electro- magnetically assisted deep drawing scheme, a series of experiments using the set-ups in Fig.4 were conducted to evaluate the effect of the integrated EMF by using a four-turn coil shown in Fig.5 and the 30 kJ EMF machine at Harbin Institute of Technology, China (This apparatus consists of six 120 μF capacitors totally charged to the maximum voltage up to 9 kV to provide an energy storage of about 30 kJ). Fig.6 shows the changes of outer bottom radii of the final formed parts with varying discharge voltage. An apparent decrease of bottom corner radius with increasing discharge voltage can be observed, and a much smaller radius without tearing can also be achieved than that could be theoretically deformed by a 5 mm-radius punch, which indicates the enhanced formability in this process. The comparison of parts formed under different forming conditions is shown in Fig.7 with rb of 5 mm and discharge voltage of 5.75 kV for electromagnetically assisted cylindrical deep drawing process. The experi- mental results give reasonable evidence for the efficiency of the established electromagnetically assisted deep drawing scheme and the enhanced formability that exhibited beyond traditional deep drawing process for manufacturing aluminum alloy sheets in this work.
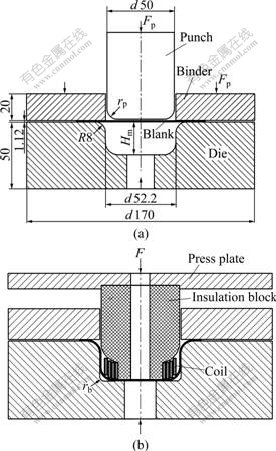
Fig.4 Schematic of electromagnetically assisted deep drawing: (a) Pre-forming; (b) Final forming

Fig.5 Photograph of coil structure for EMF process

Fig.6 Relationship between discharge voltage and bottom corner radius

Fig.7 Comparison of cylindrical parts formed by EMAS and traditional deep drawing: (a) Pre-forming (with 8 mm-radius punch); (b) EMAS (5.75 kV); (c) Traditional deep drawing (with 5 mm-radius punch)
4 Numerical modeling
Much different from conventional stamping or EMF, materials undergo a combined quasi-static and high-velocity dynamic deformation period in EMAS. To get a full understanding of deformation mechanism and characteristics, the numerical models are tentatively established for EMAS based on the specified electromagnetically assisted deep drawing process as mentioned before. Geometry parameters in simulations are the same with experiments.
4.1 “Multi-step, loose coupling” numerical scheme
According to its deformation characteristics, we can regard an EMAS process as a “multi-step” forming process, dividing the whole process into a series of separate forming sub-steps consisting of quasi-static stamping and EMF, respectively. The latter deformation sub-step should obtain the deformation information from the former one, and thus a successive deformation sequence is exhibited. Under considering the complex non-linear characteristics of contact and friction algorithms, and the high-speed dynamic behavior, the explicit code LS-DYNA is used to calculate the whole deformation process. In the EMF phase, a “loose coupling” method[7-8] is chosen to simulate the coupled multi-physics environments. On the whole, the full restart method is applied to linking deformation sub-steps. Fig.8 shows the proposed “multi-step, loose coupling” numerical scheme for the Stamping-EMF process of electromagnetically assisted deep drawing, on the basis of ANSYS Multiphysics/LS-DYNA software platform, in which the deformed geometry and magnetic loadings are extracted and again applied by user-defined subroutines using APDL language.
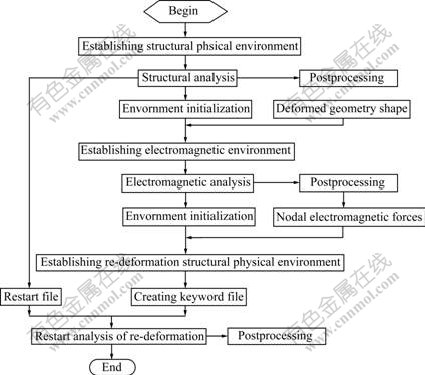
Fig.8 Flow chart of finite element analysis for Stamping-EMF process
4.2 Finite element preprocessing
The constitutive behavior of AA5052-O sheet is described by Eq.(1), obtained on the Instron-5569 electrical tensile testing machine:
σ=364.16ε0.25 (1)
where s is the true stress, and e is the true strain. In the quasi-static stamping phase, the strain rate sensitivity is ignored, while for the high-speed EMF phase, the quasi-static data are scaled, to adapt the high-strain-rate conditions by means of the Cowper-Symonds constitutive model[8]:
 (2)
(2)
where sy is the quasi-static flow stress (by Eq.(1)); ![]() is the plastic strain rate (s-1); p=6 500 s-1 and m=0.25 are specific parameters for aluminum.
is the plastic strain rate (s-1); p=6 500 s-1 and m=0.25 are specific parameters for aluminum.
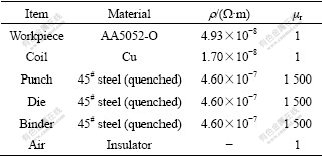
The finite element models for the system of electromagnetically assisted deep drawing are shown in Fig.9, and only half view of the forming system is considered in both phases for its axial symmetry. The pre-forming model is shown in Fig.9(a) and the explicit finite element PLANE162 is chosen to divide the model, while the electromagnetic element PLANE53 and INFIN110 are applied to the EMF model shown in Fig.9(b). Finer meshes are used to describe the regions of the coil and the sheet for taking the skin effect of the sheet into account and obtaining the reliable results. The electromagnetic parameters for the EMF system are given in Table 1.
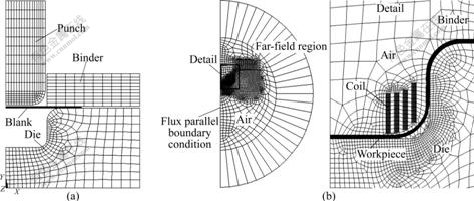
Fig.9 Finite element model for electromagnetically assisted cylindrical deep drawing system: (a) Structural field for pre-froming stage; (b) Electromagnetic field for EMF stage and detail including coil and sheet
Table 1 Electromagnetic parameters for electromagnetically assisted deep drawing system
The displacement control curve with a trapezoidal velocity profile is used as the input loading in the quasi-static stamping phase. Mass scaling is used for computational efficiency of the analysis[9] and the tool (punch) velocity is set at 3 m/s for speed scaling.
A pulse of current through the coil is the load in the electromagnetic model, which is easily measured by experiments. The first half period of the current is considered to be responsible for the EMF phase. In EMF, the current is approximately expressed by[10-11]
![]() (3)
(3)
where U is the discharge voltage; C=720 μF is the total capacitance of the capacitor bank; t0=240 μs is the cyclic; and b=3 320 s-1 is the damping exponent. The boundary conditions for EMF simulation can be established according to Refs.[12-13].
5 Deformation analysis of electro- magnetically assisted deep drawing
5.1 Deformation evolution of sheet
Fig.10 shows the deformation and effective plastic strain evolution versus time, for which the time ranging from 0 to 10.5 ms is the quasi-static deep drawing period and the followed 120 μs is the EMF period. As can be seen, the whole deformation process of sheet consists of two distinct periods, total deep drawing and local deformation of bottom corner region. And the effective plastic strain evolution shows a successive deformation as a whole, indicating that the deformation information communicates between the two kinds of forming sub-steps. This gives evidence for the feasibility of the proposed numerical scheme to simulate successive material responses in an EMAS process. Fig.11 shows the displacement and velocity evolution of the center position in the bottom corner region during the whole performance. A combined quasi-static/dynamic deforma- tion sequence versus time can be observed from Fig.11, indicating the typical material response of EMAS. Also, at the beginning of EMF phase, the magnetic pressure is too small to launch the sheet. As a result, an apparent time delay is observed for the nonsynchronous initiations of discharge of capacitor and sheet deformation[14]. This kind of time delay is related with discharge energy, discharge frequency and material parameters and so on. When the magnetic pressure becomes larger than the flow stress of materials with increasing discharge current, the re-deformation at the bottom corner launches, and the deformation velocity first increases then decreases. This process reflects the typical EMF deformation characteristics[7]. However, for the pre-forming of materials has introduced work-hardening, this time delay will be much longer. And also the deformation has a slightly rebound for the elastic effect in the high-speed die-sheet impact is much more remarkable.
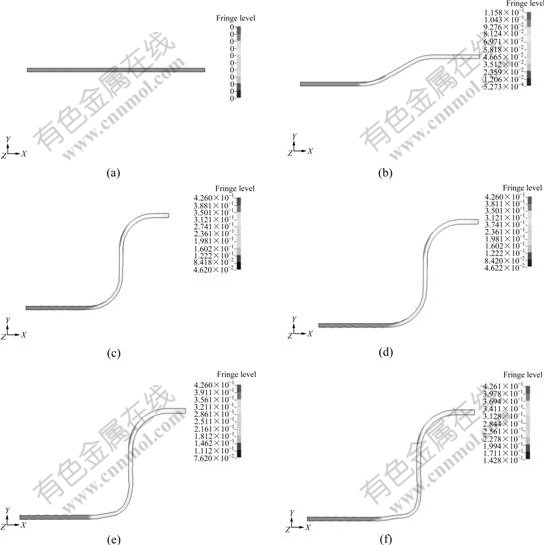
Fig.10 Deformation and effective plastic strain evolution versus time: (a) 0 ms; (b) 3.675 ms; (c) 10.5 ms; (d) 10.5 ms+6 ms; (e) 10.5 ms+60 ms; (f) 10.5 ms+120 ms
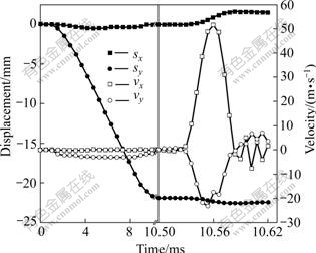
Fig.11 Nodal displacement(s) and velocity evolution(v) vs time in bottom corner region
In order to validate the efficiency of numerical results, the predicted geometry is compared with the experimental result, as shown in Fig.12. The measured points are located on the side wall and in bottom corner region of the part. As can be seen, the measured experimental profiles and numerical results are in good agreement, although the height (including the thickness of flange region) of experimental part (about 26 mm) is slightly bigger than the predicted height (25.2 mm).
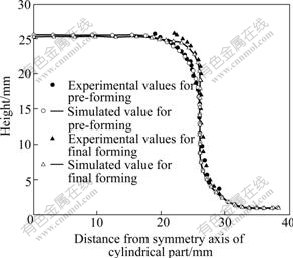
Fig.12 Predicted and experimental profiles deformed by electromagnetically assisted deep drawing
5.2 High-speed deformation behaviors in local bottom corner region
For the Stamping-EMF process, local EMF of bottom corner is the key forming process, while quasi-static deep drawing plays an assistance role. Generally, EMF happens on the order of hundreds of inertia effect (or stress-wave effect) and strain rate effect is very remarkable[15]. Fig.13 shows the magnetic force distributions in the bottom corner region. In the EMF phase, magnetic forces are mainly concentrated in the local region of bottom corner and exhibit apparently as body forces. This kind of distribution characteristic of magnetic forces will also make the deformation concentrated in the bottom region. Three typical locations in the bottom corner region are chosen (Fig.14), and their displacement and velocity evolution are shown in Fig.15. During the corner-fill performance, the locations close to the side wall (S) and close to the bottom (B) have an apparent trend of moving into the corner along the tangent direction, while the location of the center (C) has a moving trend along its normal direction. In addition, position C has a much higher radial velocity than that of position B, while position S has an axial velocity much lower than position C. The gradient distributions of velocities along these two vertical directions will at last result in local high-speed bulging trend in the corner region, which will induce severely two thickness-thinning regions at the location close to the side wall and the location near bottom region, verified by the experimental results shown in Fig.16. Besides, it is noted that, from Fig.15(a), although there is not so much difference between the radial displacements of locations B and C, their radial velocities differ greatly. This phenomenon may give explanation for the greatest wall-thinning region (in Fig.16) near the bottom region. Compared with the existing of only one thickness-thinning region in traditional deep drawing process, the high-speed corner-fill performance in electromagnetically assisted deep drawing process could diffuse deformation and thus enhance the formability of materials.
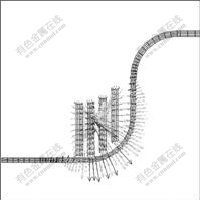
Fig.13 Magnetic force distributions in EMF phase
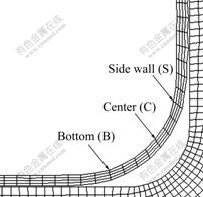
Fig.14 Schematic of typical locations in bottom corner region
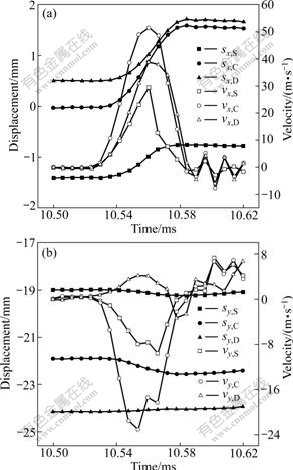
Fig.15 Nodal displacement(s) and velocity evolution(v) of typical locations in bottom corner region: (a) Along radial direction; (b) Along axial direction
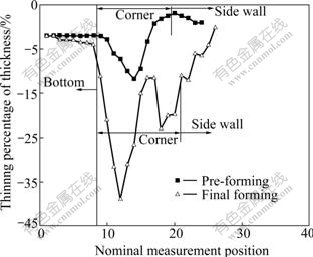
Fig.16 Distributions of wall thickness thinning on cylindrical parts
6 Conclusions
1) Under the specific conditions, the established electromagnetically assisted deep drawing process can significantly enhance the formability of AA5052-O sheet over conventional deep drawing process, and accordingly, the feasibility of what EMAS can improve the formability of aluminum sheet is validated.
2) A “multi-step, loose coupling” numerical scheme is tentatively proposed and is successfully applied to simulate the Stamping-EMF process of electro- magnetically assisted deep drawing, which provides the basis for further investigating the deformation mechanism of EMAS.
3) The proposed numerical method is validated by the results of the deformed sheets in experiments. The predicted and experimental profiles of cylindrical parts are in good agreement. And the predicted deformation characteristics of sheet metal reflect experimental results.
References
[1] SATIO M, IWATSUKI S, YASUNAGA K. Development of aluminum body for the most fuel efficient vehicle [J]. JSAE Review, 2000, 21(1): 511-516.
[2] GOLOVASHCHENKO S F. Material formability and coil design in electromagnetic forming [J]. Journal of Materials Engineering and Performance, 2007, 16: 314-320.
[3] DAEHN G S, VOHNOUT V J, DATTA S. Hyperplastic forming: Process potential and factors affecting formability [J]. Mat Res Soc Symp Proc, 2000, 601: 247-252.
[4] VOHNOUT V J. A hybrid quasi-static/dynamic process for forming large sheet metal parts from aluminum alloys [D]. Ohio: The Ohio State University, 1998.
[5] VOHNOUT V J, DAEHN G H, SHIVPURI R. A hybrid quasi-static-dynamic process for increased limiting strains in the forming of large sheet metal aluminum parts [C]// Advanced Technology of Plasticity 1999. Proceedings of the 6th ICTP. Nuremberg, 1999: 1359-1364.
[6] SHANG J H. Electromagnetically assisted sheet metal stamping [D]. Ohio: The Ohio State University, 2006.
[7] OLIVEIRA D A, WORSWICK M J, FINN M. Simulation of electromagnetic forming of aluminum alloy sheet [J]. SAE 2001 World Congress. Detroit: 2001-01-0824.
[8] MAMALIS A G, MANOLAKOS D E, KLADAS A G, KOUMOUTSOS A K. Electromagnetic forming tools and processing conditions: Numerical simulation [J]. Materials and Manufacturing Processes, 2006, 21: 411-423.
[9] ZHAO Hai-ou. LS-DYNA dynamic analysis guide [M]. Beijing: Ordnance Industrial Publishing House, 2003: 123-127. (in Chinese)
[10] YU Hai-ping. Buckling criterion and deformation analysis of electromagnetic tube-compression [D]. Harbin: Harbin Institute of Technology, 2006: 52-88. (in Chinese)
[11] LI Zhong, LI Chun-feng, ZHAO Zhi-heng. Some measurements of electromagnetic forming [J]. Journal of Plasticity Engineering, 2004, 11(4): 81-84. (in Chinese)
[12] LEE S H, LEE D N. A finite element analysis of electromagnetic forming for tube expansion [J]. Journal of Engineering Materials and Technology, 1994, 16: 250-254.
[13] LEE S H, LEE D N. Estimation of the magnetic pressure in tube expansion by electromagnetic forming [J]. Journal of Materials Processing Technology, 1996, 57: 311-315.
[14] YU Hai-ping, LI Chun-feng. Numerical modeling methods of electromagnetic forming and analysis of electromagnetic tube-compression [J]. Materials Science & Technology, 2004, 12(5): 536-539. (in Chinese)
[15] MEYERS M A. Dynamic behavior of materials [M]. ZHANG Q M, et al. Beijing: National Defense Industry Press, 2006: 225-300. (in Chinese)
Foundation item: Project(50805036) supported by the National Natural Science Foundation of China
Corresponding author: LIU Da-hai; Tel: +86-451-86413970; Fax: +86-451-86418753; E-mail: dahai_liu@126.com
DOI: 10.1016/S1003-6326(08)60441-0


