
First-principles study of bulk and (001) surface of TiC
FANG Li-hong(房立红)1, WANG Li(王 丽)2, GONG Jian-hong(宫建红)2,
DAI Hong-shang(戴洪尚)1, MIAO De-zhuang(苗德壮)1
1. Key Laboratory of Liquid Structure and Heredity of Materials, Ministry of Education,
Shandong University, Ji’nan 250061, China;
2. School of Mechanical and Electronic Engineering, Shandong University at Weihai, Weihai 264209, China
Received 23 March 2009; accepted 15 June 2009
Abstract:
The structural and electronic properties of bulk and (001) plane of TiC were investigated by the first-principles total-energy pseudopotential method based on density functional theory. The calculated bulk properties indicate that bonding nature in TiC is a combination of ionicity, covalency and metallicity, in which the Ti—C covalent bonding is the predominate one. The calculated results of structural relaxation and surface energy for TiC(001) slab indicate that slab with 7 layers shows bulk-like characteristic interiors, and the changes of slab occur on the outmost three layers, which shows that the relaxation only influences the top three layers. Meanwhile, the strong Ti—C covalent bonding can be found in the distribution of charge density on the (110) and (001) planes. Ti—C covalent bonding is enhanced by the charge depletion and accumulation in the vacuum and the interlayer region between top two atomic layers.
Key words:
first-principles; TiC; charge transfer; structural relaxation;
1 Introduction
As one of transition-metal carbides, TiC possesses not only many special physical properties, such as high melting point, extreme hardness, and outstanding wear resistance, but also exhibits high electric and heat conductivity, which makes it highly attractive in the scientific and technological region[1]. It is widely used in the particulate-reinforced composites[2], grain refiner[3], microelectro-mechanical systems[4], fusion- reactor walls[5], biocompatible materials[6], etc. The experimental[7-8] and theoretical[9-11] studies on TiC cover the fields of materials science, physics as well as chemistry. A relatively large amount of first-principle calculation has been devoted to study the bulk properties, surface and interfacial properties of TiC. AHUJA and ERIKSSON[11] calculated the structural and elastic properties of TiC using the full potential linear muffin-tin orbital method in 1996. JOCHYM et al[12] examined the phonon dispersion and phonon density of states for the TiC crystal. The results are compared and show a good agreement with the experimental neutron scattering data. LIU et al[13] examined electronic structure and adhesion of polar TiC(111)/Ti interfaces. Recently, the adsorption on TiC(111) surface has also been investigated with density functional calculation[1]. However, there is few research of structural and electronic properties of TiC based on grain refinement. The purpose of the present work is to study the electronic and bonding properties of bulk and (001) surface of TiC. In addition to its appeal from a basic science standpoint, the final motivation for the study of TiC is to explore the grain refinement mechanism of Al-Ti-C master alloys in the future.
2 Methodology
For this study, we utilized the CASTEP (Cambridge Serial Total Energy Package)[14] in our calculations, based on density functional theory (DFT). CASTEP uses a plane wave basis set for the expansion of the single particle Kohn-Sham as implemented and ultrasoft pseudopotentials to describe ionic cores. The exchange-correlation energy was described by generalized gradient approximation of PBE(GGA-PBE). The Brillouin zone was sampled with Monkhorst-Pack k-point grid. For the bulk and slab, a [8×8×1] k-point mesh was used. The plane-wave cutoff energy in our calculations was 350 eV, which assured a total-energy convergence of 2.0×10-5 eV/atom. The diagrams of distribution of charge density and difference in charge density were obtained with the ORIGIN package.
3 Bulk and surface calculations
3.1 Bulk properties
3.1.1 Optimization of structure
To assess the accuracy of our computation method, in particular, of the pseudopotentials used, we performed a series of calculations on the bulk properties of TiC. Firstly, we constructed a diagram for the bulk of TiC as Fig.1. Table 1 shows our results, other calculated and experimental results of the lattice constants, bulk modulus, cohesive energies and heat of formation of bulk TiC.
Fig.1 Schematic diagram of bulk TiC
Table 1 Calculated lattice constant, bulk modulus, cohesive energy and heat of formation of bulk TiC compared with other calculations and experimental data

From the results listed in Table 1, we can find that our calculated results are in satisfactory agreement with the results of other calculations and the experimental values. Thus, this proves that our results have sufficient accuracy.
3.1.2 Electronic structure
The calculated result of band structure within GGA for TiC is shown in Fig.2(a). The low-lying energetically band is derived from 2s states of C atom. The three overlapping bands originating from the state at G point are found, mainly composed of 2p states of C atom. The next bands around Fermi level are derived from Ti 3d states. The detailed analysis on the electronic structure is shown in Fig.2(b), which is the total density of states (DOS) of bulk TiC. Fig.3 shows the partial density of states (PDOS) of C 2s,C 2p, Ti 3s/4s, Ti 3p, Ti 3d for bulk TiC.
There are six main peaks (A, B, C, D, E and F) in the total density of states (DOS) curve of TiC. The peaks of A and B in the lower energy part of the DOS curve arise from the Ti 3s and Ti 3p states, respectively, which are localized and contribute few to the bonding of TiC. The peak of C is dominated by C 2s states and its effect on bonding is very small[15]. The integrated intensity of the C 2s state below the Fermi energy is about 1.5 from the PDOS curve, less than 2, which indicates that there are a small amount of charge transfer from C 2s to C 2p. The broad peaks of D and E, which are mainly composed of C 2p and Ti 3d states form a wide band (a “pseudogap” between the peak D and E), centered at about the Fermi energy and their characteristics of the
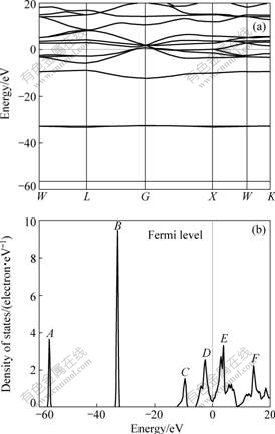
Fig.2 Calculated band structure (a) and total density of states (DOS) (b) of TiC
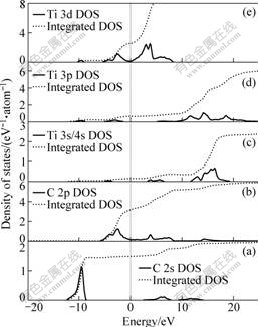
Fig.3 Partial density of states (PDOS) of C 2s (a), C 2p (b), Ti 3s/4s (c), Ti 3p (d), Ti 3d (e) for bulk TiC
states below the Fermi energy are both large and show a strong correlation from the PDOS curve, indicating that the substantial covalent bonding exits. It is the Ti-C covalent interactions resulting from the d-p hybridization of Ti and C atoms that are the main reason for the creation of pseudogap, as a result of a large contribution of covalent bonding between the C 2p and Ti 3d states to the cohesive energy of TiC. The lowest value of DOS is about 0.3 eV-1?atom-1 but not 0 at the Fermi energy (Ef), as shown in Fig.2(b), confirming the metallic characteristic of crystal, which can be attributed to Ti 3d and C 2p states, as shown in Figs.3(b) and (e).
The upper peak of F is attributed to the Ti 4s states which lies above the Fermi level, so that the electronic charge in this state is forced to diffuse to the Ti 3d and C 2p states. Therefore, the charge transfer from Ti to C occurs in TiC compound, and an ionic bonding is formed, contributing partially to the cohesive energy. The fact that the sum of the integrated intensities of the C 2s and 2p states is beyond 4 from the PDOS curve implies that parts of the lost valence electrons of Ti atoms are transferred to C atoms. The other part of the lost valence electrons contributes to the incremental free-electron states of the Ti 3d, as shown in Fig.3(e). Nearly free electron states of the Ti 3d are the main reason for non-zero value of the Fermi energy. Generally, the bonding in TiC can be classified as a combination of metallic, ionic and covalent characteristics, in which Ti—C covalent bonding constitutes the main part, and a certain degree of ionicity can be detected, combined with a smaller amount of metallic bonding.
Figs.4(a) and (b) present the distribution of valence charge density and difference valence charge density on the (001) plane of bulk TiC. It is obviously shown that strong interaction exists between the C and Ti atoms in Fig.4(a), which results in the occurrence of pseudogap in the DOS curves. We can see from Fig.4(b) that the charge transfer from Ti to C is significant, although there is a large hybridization of Ti 3d and C 2p states. From the analysis of Mulliken population results on Table 2, it is found that the electron number of Ti 4s is only 2.13. The lost electrons of Ti 4s (1.87) have three traces. Since the electron number on Ti 3p states is 6.60, extra 0.60 electrons come from the transformation of Ti 4s orbits. About 0.59 electrons on the Ti 3d states originate from the lost Ti 4s state, which both contribute to the metallic bonding in TiC. The lasting electrons on Ti 4s states are transferred to C 2p orbits, as a result of the ionic bonding. The electron transformation from C 2s to C 2p orbits is observed in Table 2. The extra 1.19 electrons in C 2p states come from the lost valence electrons of 0.51 on the C 2s states and 0.68 electrons on the Ti 4s states after bonding.
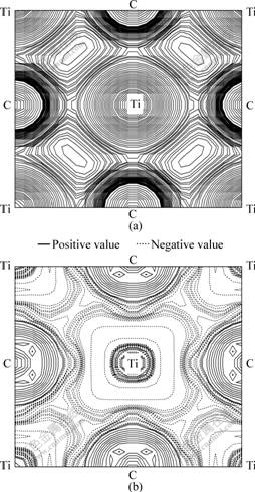
Fig.4 Distribution of charge density (a) and difference in charge density (b) on (001) plane for bulk TiC after optimization of structure
Table 2 Mulliken population analysis results of TiC
3.2 Surface properties
First of all, we need to construct a TiC(001) slab for the calculation. Through cleaving a bulk TiC after geometry optimizing, we could get the TiC slab shown in Fig.5. It is a three-dimensional system. In order to prevent the interaction between the slab and its periodic images, a vacuum region of 20 ? is included in the supercell.

Fig.5 Schematic diagram of TiC(001) slab with seven layers
3.2.1 Structural relaxations and judgment of surface convergence
Table 3 lists the results of TiC(001) surface relaxations as a function of slab thickness. It is indicated that the crystal structure of (001) free surface is within a very small change and surface reconstruction does not occur for TiC(001) surface after full relaxation. It is also shown that the surface relaxation is larger on the top atomic layers of the TiC slab. The C atoms displace outward and their intervals are larger, while the Ti atoms displace inward and their intervals are smaller on the top three atomic layers, which is consistent with the conclusion in other report[16]. The expansion/ contraction effect does not happen on moving into deeper layers. Relaxation for (001) surface is not large, and the effects of relaxation are mainly localized within the top three atomic layers. When the slab thickness, n, is more than 7, the top three interlayer relaxations for (001) surface is well converged, which implies that the slabs
Table 3 TiC(001) surface relaxations as function of slab thickness (change of interlayer spacing Δij as percentage of spacing in bulk)
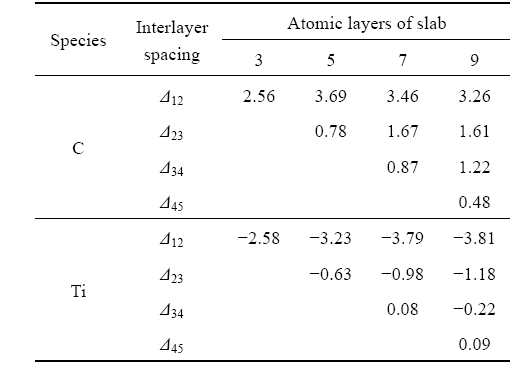
with more than 7 atomic layers possess the bulk-like characteristic interiors.
Since the properties for thin slab differ significantly from those of thick one[8], it is important to make sure that TiC slab is thick enough to show the bulk-like characteristic interiors, which would lead to a large amount of computation. Therefore, the minimum number of atomic layers should be determined to satisfy both the slabs with bulk-like characteristic interiors and lower computation cost. A preliminary analysis in Table 3 indicates that the slabs with 7 atomic layers possess the bulk-like interior. Surface energy calculation is performed to further identify the minimum number of atomic layers. Since TiC(001) is a non-polar surface, one way to ensure the presence of a bulk-like slab is to check for the convergence of the surface energy with respect to the number of atomic layer, n[8]. Upon attaining a critical thickness, the surface energy will converge to a fixed value, indicating that the TiC slab possesses a bulk-like interior. We have calculated the surface energy for the (001) surface of the slabs with sizes ranging from 3 to 9 layers based on the method proposed by BOETTGER[17]:
![]() (1)
(1)
where ![]() is the total energy of a n-layer slab; and ?E is the incremental energy determined by
is the total energy of a n-layer slab; and ?E is the incremental energy determined by ![]()
As can be seen in Table 4, the surface energy for the TiC(001) surface converges rapidly with increasing slab thickness to about 1.58 J/m2 for slabs with n≥7. Our calculated surface energy of 7-layer is consistent with other calculated value[10]. Therefore, 7-layer slab of TiC(001) is chosen for further studies on the electronic structure.
Table 4 Convergence of surface energy with respect to slab thickness

3.2.2 Electronic structure
Table 5 lists the effective atomic charges for TiC(001) unrelaxed and relaxed surfaces using Mulliken population analysis. It is found that the effective atomic charges for the atoms from the upper layers to the inner layers differ slightly after full relaxation, which implies that the charge transfers between the top two layers are small. Thus, it is impossible for the small charge transfers to impact the distribution of chemical bonds between atoms of the research system. The lattice structure has not been changed significantly after full relaxation.
Table 5 Effective atomic charges for TiC(001) surfaces
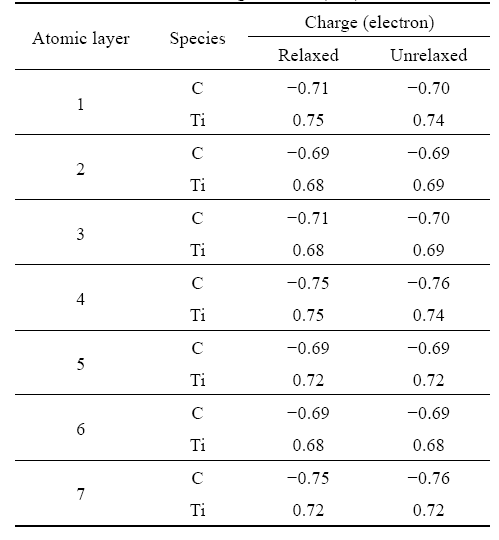
To further analyze the electronic structures of the surfaces, the distributions of valence charge density of relaxed surfaces and the differences in the charge densities between the relaxed and unrelaxed surfaces on the (110) and (001) plane for TiC(001) surfaces are shown in Fig.6 and Fig.7, respectively.
It can be seen in Fig.6(a) that strong Ti-C interaction exists between Ti atoms and C atoms, which is also observed in the distribution of charge density on the (001) plane for bulk TiC, as shown in Fig.4(a). It can also be seen in Fig.6(b) that the relaxation only influences the top three layers, which is consistent with the results in Table 3. Charge depletion happens in the upper vacuum of Ti atoms and there is charge
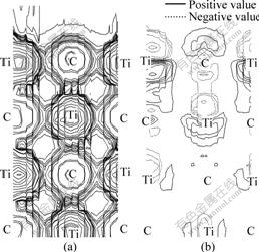
Fig.6 Distribution of charge density (a) and difference in charge density (relative to ideal surface) (b) on (110) plane for TiC(001) surface after full relaxation
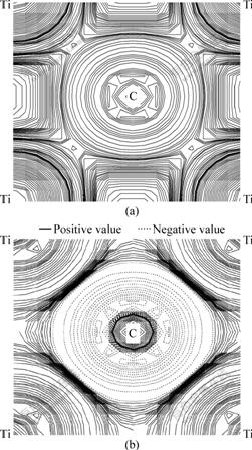
Fig.7 Distribution of charge density (a) and difference in charge density (relative to ideal surface) (b) on (001) plane for TiC(001) surface after full relaxation
accumulation between the first and second layers after full relaxation; while charge accumulation happens in the upper vacuum of C atoms and charge depletion happens in the interlayer, which leads to a conclusion that the chemical bonding between Ti and C atoms are reinforced. We also find charge accumulation and depletion between the second and three layers, but there is just a small amount. Meanwhile, there are few charge transfers in the interior of the TiC slab, which further confirms the little effect of full relaxation on the inner layers.
The distribution of charge density and difference in charge density (relative to the ideal surface) on the (001) plane for the TiC(001) surface is shown in Figs.7(a) and (b), respectively. Like Fig.4(a) and Fig.6(a), the distribution of charge density on the (001) plane shown in Fig.7(a) also reveals the strong interaction between Ti and C atoms. Moreover, it is suggested from Fig.7(b) that C atoms lose electrons and Ti atoms get electrons after full relaxation. We can make an explanation with Fig.6(b). As mentioned above, for the Ti atoms on the surface, charge accumulation happens between the first and second layers; for the C atoms on the surface, charge depletion happens after full relaxation. Therefore, it is the existence of free surface that leads to the changes of charge transfers.
4 Conclusions
1) The bonding nature in TiC can be classified as a combination of metallic, ionic and covalent characteristics, in which Ti—C covalent bonding is the main part. A certain degree of ionicity can be detected, combined with a smaller amount of metallic bonding.
2) It is found that the crystal structure of (001) free surface has a very small change and surface reconstruction does not happen for TiC(001) surface after full relaxation. The changes of slab occur on the outmost three layers.
3) As the number of layers reaches 7, the surface energy is converged, indicating that slab with 7 layers shows bulk-like characteristic interiors.
4) The strong Ti—C covalent bonding can be found on the (110) and (001) planes and it is enhanced by the charge depletion and accumulation in the vacuum and interlayer region between atomic layers.
References
[1] RUBERTO C, LUNDQVIST B I. Nature of adsorption on TiC(111) investigated with density-functional calculation [J]. Phys Rev B, 2007, 75: 235438-1-31.
[2] PENG L M. Synthesis and mechanical properties of niobium aluminide-based composites [J]. Mater Sci Eng A, 2008, 480: 232-236.
[3] WANG Z Q, LIU X F, LIU Y H, ZHANG J Y, YU L N, BIAN X F. Structural heredity of TiC and its influences on refinement behaviors of AlTiC master alloy [J]. Trans Nonferrous Met Soc China, 2003, 13: 790-793.
[4] SONG M S, HUANG B, ZHANG M X, LI G J. Study of formation behavior of TiC ceramic obtained by self-propagating high-temperature synthesis from Al–Ti–C elemental powders [J]. Int Journal of Refractory Metals & Hard Materials, 2009, 27: 584-589.
[5] HOJOU K, OTSU H, FURUNO S, SASAJIMA N, IZUI K. In situ observation of damage evolution in TiC during hydrogen and deuterium ion irradiation at low temperatures [J]. Journal of Nuclear Materials, 1996, 239: 279-283.
[6] JONES M I, MCCOLL I R, GRANT D M, PARKER K G, PARKER T L. Protein adsorption and platelet attachment and activation, on TiN, TiC, and DLC coatings on titanium for cardiovascular applications [J]. Journal of Biomedical Materials Research, 2000, 54: 413-421.
[7] DUNAND A, FLACK H D, YVON K. Bonding study of TiC and TiN. I. High-precision X-ray-diffraction determination of the valence-electron density distribution, Debye-Waller temperature factors, and atomic static displacements in TiC0.94 and TiN0.99 [J]. Phys Rev B, 1985, 31: 2299-2315.
[8] LIU L M, WANG S Q, YE H Q. Adhesion and bonding of the Al/TiC interface [J]. Surface Science, 2004, 550: 46-56.
[9] DUDIY S V, LUNDQVIST B I. First-principles density-functional study of metal-carbonitride interface adhesion: Co/TiC(001) and Co/TiN(001) [J]. Phys Rev B, 2001, 64: 045403-1-14.
[10] ARYA A, CARTER E A. Structure, bonding, and adhesion at the TiC(100)/Fe(110) interface from first principles [J]. The Journal of Chemical Physics, 2003, 118: 8982-8996.
[11] AHUJA R, ERIKSSON O. Structural, elastic, and high-pressure properties of cubic TiC, TiN, and TiO [J]. Phys Rev B, 1996, 53: 3072-3079.
[12] JOCHYM P T, PARLINSKI K, STERNIK M. TiC lattice dynamics from ab initio calculations [J]. Eur Phys J B, 1999, 10: 9-13.
[13] LIU L M, WANG S Q, YE H Q. First-principles study of the polar TiC/Ti interface [J]. J Mater Sci Technol, 2003, 19: 540-544.
[14] SEGALL M D, LINDAN P J D, PROBERT M J, PICKARD C J, HASNIP P J, CLARK S J, PAYNE M C. First-principles simulation: Ideas, illustrations and the CASTEP code [J]. J Phys: Cond Matt, 2002, 14: 2717-2744.
[15] PRICE D L, COOPER B R. Total energies and bonding for crystallographic structures in titanium-carbon and tungsten-carbon systems [J]. Phys Rev B, 1989, 39: 4945-4957.
[16] PRICE D L, WILLS J M, COOPER B R. TiC(001) surface relaxation [J]. Physical Review Letters, 1996, 77: 3375-3378.
[17] BOETTGER J C. Nonconvergence of surface energies obtained from thin-film calculations [J]. Phys Rev B, 1994, 49: 16798-16800.
(Edited by YANG Bing)
Foundation item: Project(200802015) supported by Post-doctoral Foundation of Shandong Province, China; Project(50625101) supported by the National Natural Science Foundation for Distinguished Young Scholars of China
Corresponding author: WANG Li; Tel: +86-531-88396020; E-mail: wanglihxf@sdu.edu.cn
DOI: 10.1016/S1003-6326(09)60226-0


