J. Cent. South Univ. (2016) 23: 944-954
DOI: 10.1007/s11771-016-3142-9
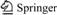
Critical embedment depth of a rigid retaining wall against overturning in unsaturated soils considering intermediate principal stress and strength nonlinearity
ZHANG Chang-guang(张常光)1, CHEN Xin-dong(陈新栋)2, FAN Wen(范文)3
1. School of Civil Engineering, Chang’an University, Xi’an 710061, China;
2. School of Highway, Chang’an University, Xi’an 710064, China;
3. School of Geological Engineering and Geomatics, Chang’an University, Xi’an 710054, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract:
The overturning stability is vital for the retaining wall design of foundation pits, where the surrounding soils are usually unsaturated due to water draining. Moreover, the intermediate principal stress does affect the unsaturated soil strength; meanwhile, the relationship between the unsaturated soil strength and matric suction is nonlinear. This work is to present closed-form equations of critical embedment depth for a rigid retaining wall against overturning by means of moment equilibrium. Matric suction is considered to be distributed uniformly and linearly with depth. The unified shear strength formulation for unsaturated soils under the plane strain condition is adopted to characterize the intermediate principal stress effect, and strength nonlinearity is described by a hyperbolic model of suction angle. The result obtained is orderly series solutions rather than one specific answer; thus, it has wide theoretical significance and good applicability. The validity of this present work is demonstrated by comparing it with a lower bound solution. The traditional overturning designs for rigid retaining walls, in which the saturated soil mechanics neglecting matric suction or the unsaturated soil mechanics based on the Mohr-Coulomb criterion are employed, are special cases of the proposed result. Parametric studies about the intermediate principal stress, matric suction and its distributions along with two strength nonlinearity methods on a new defined critical buried coefficient are discussed.
Key words:
1 Introduction
Even though saturated soils could be generally regarded as special cases of unsaturated soils with null matric suction, their mechanical properties have great differences [1-2]. Unsaturated soils in engineering practice are often acted under complex multi-axial stress state, and sometimes yield and failure in extreme circumstances [3]. What is more, true triaxial test results of unsaturated soils signified that the intermediate principal stress did have a significantly strengthening effect on the unsaturated soil strength [4-6]. The plane strain condition is a true three-dimensional stress state, where the intermediate principal stress acts in the longitudinal direction and does not equal to the two other principal stresses on the cross section. In addition, the strength of unsaturated soils was initially defined in terms of a linear increase with respect to matric suction using a constant suction angle [7]. But as time went by, it was found that the relationship between the unsaturated soil strength and matric suction could be nonlinear over a wide range of suction values [8-12]. Therefore, the strength of unsaturated soils surrounding foundation pits under the plane strain condition should be described by such a failure criterion with consideration of the intermediate principal stress and nonlinear characteristic to estimate real strength of unsaturated soils and to be used for optimizing engineering designs.
The overturning stability is an important component for the retaining wall design of complex foundation pits. Due to doing some dewatering measures in or outside foundation pits, the soils surrounding foundation pits are usually in an unsaturated state. However, routine calculations and designs against overturning for retaining walls of foundation pits are mostly based on the Mohr- Coulomb (M-C) criterion for saturated soils [13], without accounting for the effects of intermediate principal stress and matric suction on the soil strength. Furthermore, the unstable suction strength caused by matric suction that cannot be measured in conventional tests was seen as the stable cohesion of saturated soils, which makes foundation pit designs unreasonable and would result in engineering accidents in some serious conditions [1]. Only few studies to date were available for the overturning design of retaining walls in unsaturated soils [14-17], in which the influence of saturation degree, earth berm and the load and resistance factor method were addressed. The factor of stability against overturning is defined as the ratio of the resisting moment due to passive earth pressure to the driving moment due to active earth pressure at the wall toe; thus, the key of the overturning design is to identify the earth pressures acting on retaining walls. Additionally, earth pressures acting on retaining walls in unsaturated soils are prominently influenced by matric suction and are markedly different from that in saturated soils [1-2, 18-21]. These above results about the earth pressures and overturning stabilities of retaining walls in unsaturated soils are all based on the M-C criterion without considering the intermediate principal stress. ZHANG et al [22-23] established a unified shear strength formulation for unsaturated soils on the basis of the unified strength theory (UST) [24-25] by analogy method. This unified shear strength formulation not only takes into account the effect of intermediate principal stress reasonably, but also allows to reflect nonlinear strength of unsaturated soils along with a hyperbolic model of suction angle under high suction [10]. so, it has an outstanding application value. The new results of Rankine earth pressure for unsaturated soils were obtained according with the unified shear strength formulation [22, 26]. On the other hand, the magnitude and distribution of matric suction in unsaturated soils are closely associated with environmental conditions. But the existing overturning calculations of retaining walls do not consider specific distributions of matric suction. For engineering applications, two distributions of matric suction are commonly assumed [1-2]: one is that matric suction distributes uniformly with depth, and the other is that matric suction decreases linearly with depth to a value of zero at the water table.
Therefore, the primary objective of this work aims to develop closed-form equations of critical embedment depth dealing with the overturning design of a rigid retaining wall in unsaturated soils. Uniform and linear distributions of matric suction are assumed. The failure of unsaturated soils is governed by the unified shear strength formulation with a hyperbolic model of suction angle to consider the intermediate principal stress and strength nonlinearity. This result proposed is further verified through comparisons with the lower bound solution. In addition, parametric studies are conducted to investigate the effects of the intermediate principal stress, matric suction and its distributions and strength nonlinearity on a new defined critical buried coefficient. The sliding failure of retaining walls and stress state of soils below retaining walls are beyond the scope of this study.
2 Basic theories
In the process of constructing foundation pits, some dewatering measures are often carried out to drop the water table below the excavation depth. The rigid retaining wall and its surrounding soils are both under the plane strain conditions. As shown in Fig. 1, a longitudinal unit length of the rigid retaining wall in the middle of a foundation pit is presented, where H is the excavation depth of the foundation pit, D(Dl) is the (critical) embedment depth of the retaining wall and yot is the tension zone depth of the soil behind the retaining wall. The self-weight of the retaining wall, other supporting effects and ground surcharge are neglected. The water table Dw is always considered to be located below the toe of the wall.

Fig. 1 A rigid retaining wall of foundation pits
2.1 Unified shear strength formulation for unsaturated soils under plane strain condition
By combining YU’s UST [24-25] and FREDLUND’s theory of two stress state variables [7], ZHANG et al [22-23] derived the unified shear strength formulation for unsaturated soils under the plane strain condition with analogy method. The unified shear strength τf under the plane strain condition is expressed as
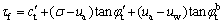 (1)
(1)

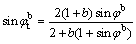
where c′ is the effective cohesion and ct′ is the unified effective cohesion; φ′ is the effective angle of internal friction and φt′ is the unified effective angle of internal friction; ua is the pore-air pressure, uw is the pore-water pressure and (ua-uw) is matric suction; σ is the total normal stress and (s-ua) is the net normal stress; φb is the suction angle related with matric suction and φtb is the unified suction angle; b is the UST parameter of unsaturated soils to characterize the influence of intermediate principal stress on the soil strength, and also b is a choosing parameter of different failure criterion and the value of it is between 0 and 1 (i.e. 0≤b≤1).
The form of Eq. (1) is very similar to the shear strength equation of unsaturated soils based on FREDLUND’s theory of two stress state variables. But the value of parameter b can characterize the effect of intermediate principal stress on the unsaturated soil strength and different values correspond to different failure criteria. When b=0, Eq. (1) reduces to the shear strength equation of unsaturated soils using FREDLUND’s theory of two stress state variables and the M-C criterion without considering the intermediate principal stress effect [7]. When b=1, Eq. (1) reduces to the shear strength equation of unsaturated soils based on the twin-shear stress criterion. When 0
It is given that ctt=ct′+(ua-uw)× in which ctt is the unified total cohesion of unsaturated soils. Eq.(1) can therefore be rewritten as
in which ctt is the unified total cohesion of unsaturated soils. Eq.(1) can therefore be rewritten as
 (2)
(2)
The form of Eq. (2) is identical to the shear strength equation for saturated soils; thus, the existing derivations relevant to saturated soils can be readily modified to be suitable for unsaturated soils.
2.2 Strength nonlinearity of unsaturated soils
Over a wide range of matric suction, the suction angle φb is a nonlinear function of matric suction [8-12] and decreases with the increase of matric suction. The piecewise hyperbolic model between the suction angle φb and matric suction (ua-uw) proposed by HOUSTON et al [10] is one representative of nonlinear strength models and is expressed as
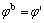 when
when 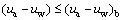 (3a)
(3a)
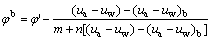 when
when
 (3b)
(3b)
where (ua-uw)b is the air-entry value of unsaturated soils; parameters m and n are the intercept and slope of the linear equation after deforming Eq. (3b) on the transformed hyperbolic plane, respectively.
From Eq. (3), it can be noted that the soil behaves as a saturated soil as long as matric suction is less than the air-entry value (ua-uw)b. Once matric suction is beyond (ua-uw)b, the suction angle φb decreases with a hyperbolic curve and then becomes stable. It is observed from Table 8 in Ref. [10] that a linear relationship between the reciprocal of slope n and the effective angle of internal friction φ′ is constructed in Fig. 2, and this fitting equation is written as
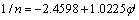 (4)
(4)

Fig. 2 Fitting slope n with effective angle of internal friction φ′
Seen from Fig. 2, the linear fitting as Eq. (4) is very favorable and is superior to that of the diagonal. Consequently, the slope n can be directly identified from the effective angle of internal friction φ′. Substituting Eqs. (3) and (4) into Eqs. (1) and (2), the novel unified shear strength formulation for unsaturated soils under the plane strain condition is obtained, which can simultaneously account for the intermediate principal stress effect and strength nonlinearity under high suction.
2.3 Distributions of matric suction
Two distributions of matric suction are assumed in this study: 1) the matric suction in Fig. 3(a) is distributed uniformly with depth, and 2) the matric suction in Fig. 3(b) decreases linearly with depth and becomes zero at the water table. The matric suction (ua-uw)y at depth of y under linear distribution is expressed as
 (5)
(5)
where (ua-uw)o is the matric suction on the ground surface and is called surface suction; y is the depth with the origin from the ground surface.

Fig. 3 Distributions of matric suction:
2.4 Earth pressures on retaining walls in unsaturated soils
It is assumed that unsaturated soils with one layer surrounding a foundation pit are uniform and continuous, and hence its horizontal earth pressures are satisfied with Rankine theory [1]. As shown in Fig. 1, the horizontal active earth pressure (sh-ua)a behind the retaining wall by using Rankine theory and the unified shear strength formulation of Eq. (1) [22] can be presented as
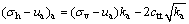 (6)
(6)
where ka is the coefficient of active earth pressure and ka=tan2(45°-φt′/2).
Substituting the net vertical stress (sv-ua)=γy (see Fig. 1) and the unified total cohesion ctt=ct′+(ua-uw)×tanφtb into Eq. (6), the active earth pressure (sh-ua)a of unsaturated soils can be revised as
 (7)
(7)
where γ is the unit weight of unsaturated soils.
By setting the active earth pressure to zero in Eq. (7) (i.e., letting (sh-ua)a=0), the tension zone depth yot of the soil behind the retaining wall can be computed as
 (8)
(8)
In addition, the soils at the bottom of the foundation pit are in a limit state of passive earth pressure (see Fig. 1). Furthermore, the passive earth pressure (sh-ua)p by using Rankine theory and the unified shear strength formulation of Eq. (1) [26] can be presented as
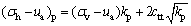 (9)
(9)
where kp is the coefficient of passive earth pressure and kp=tan2(45°+φt′/2).
By substituting the net vertical stress (sv-ua)=γ(y-H) (see Fig. 1) and the total cohesion ctt=ct′+(ua-uw)×tanφtb into Eq. (9), the passive earth pressure (sh-ua)p of unsaturated soils is also revised as
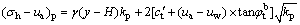 (10)
(10)
3 Critical embedment depth of retaining walls against overturning
When the factor of overturning stability is 1, the corresponding embedment depth D of the retaining wall is the critical embedment depth Dl against overturning, namely, at the toe point E of the retaining wall, the resisting moment due to the passive earth pressure is equal to the driving moment due to the active earth pressure. This condition with moment equilibrium (see Fig. 1) can be formulated as
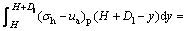
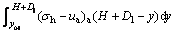 (11)
(11)
3.1 Uniform suction with depth
In the case of uniform suction with depth, the matric suction is a constant with depth that is depth-independent. Substituting Eqs. (7) and (8) into the right hand side of Eq. (11), the driving moment due to the active earth pressure is obtained as

 (12)
(12)
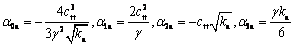
where α0a, α1a, α2a and α3a are driving moment parameters for uniform suction.
Substituting Eq. (10) into the left hand side of Eq. (11), the resisting moment due to the passive earth pressure is obtained as

 (13)
(13)


where α0p, α1p, α2p and α3p are resisting moment parameters for uniform suction.
By substituting Eqs. (12) and (13) into Eq. (11) and rearranging Eq. (11), a cubic closed-form equation describing the critical embedment depth Dl of a rigid retaining wall against overturning with uniform suction is formulated as
 (14)
(14)

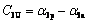
where C0U, C1U, C2U and C3U are constant coefficients for uniform suction.
3.2 Linear suction with depth
In the case of linear suction with depth, the matric suction is determined from Eq. (5). By substituting Eq. (5) into Eqs. (7) and (8), the active earth pressure (σh-ua)a and the tension zone depth yot are obtained, respectively, as
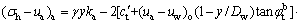
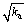 (15)
(15)
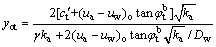 (16)
(16)
Substituting Eqs. (15) and (16) into the right hand side of Eq. (11), the driving moment of the retaining wall with linear suction is obtained as

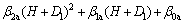 (17)
(17)

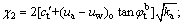

where χ1 and χ2 are intermediate parameters for linear suction; β0a, β1a, β2a and β3a are driving moment parameters for linear suction.
By substituting Eq. (5) into Eq. (10), the passive earth pressure (sh-ua)p with linear suction is achieved as

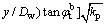 (18)
(18)
Substituting Eq. (18) into the left hand side of Eq. (11), the resisting moment of the retaining wall with linear suction is achieved as

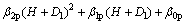 (19)
(19)


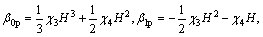

where χ3 and χ4 are intermediate parameters for linear suction; β0p, β1p, β2p and β3p are resisting moment parameters for linear suction.
By substituting Eqs. (17) and (19) into Eq. (11) and also rearranging Eq. (11), a cubic closed-form equation describing the critical embedment depth Dl of a rigid retaining wall against overturning with linear suction is formulated as
 (20)
(20)

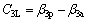
where C0L, C1L, C2L and C3L are constant coefficients for linear suction.
For practical engineering applications, the tension zone depth yot should be first calculated from Eq. (8) and Eq. (16), which corresponds to uniform suction and linear suction, respectively. Then, a comparison is made between the tension zone depth yot and the excavation depth H. If yot≥H, the foundation pit can be stable by itself, and a retaining wall is not required, while if yot
3.3 Comparability analysis
The critical embedment depth Dl against overturning calculated through closed-form Eq. (14) or Eq. (20) is not a special answer but is a set of orderly series solutions; thus, it has broad applicability due to considering the comprehensive effects from intermediate principal stress (parameter b), excavation depth (parameter H), matric suction and its distribution (parameters (ua-uw), (ua-uw)o and Dw), strength nonlinearity (parameters m and n) and effective shear strength (parameters c′and φ′).
In the case of (ua-uw)=0 kPa, Eq. (14) and Eq. (20) have the same results, and both revert to the critical embedment depth equations for saturated soils based on the UST. When parameter b=0 and 1, the overturning designs of a rigid retaining wall in saturated soils are based on the M-C criterion and the twin-shear stress criterion, respectively. In the case of (ua-uw)>0 kPa for unsaturated soils, when parameter b=0, Eqs. (14) and (20) are the overturning designs based on FREDLUND’s theory of two stress state variables and the M-C criterion; when b=1, Eqs. (14) and (20) are the optimal overturning design based on the twin-shear stress criterion; when 0
3.4 Comparisons with results of AMABILE et al [16]
According to the lower bound theorem of plasticity with the M-C criterion, AMABILE et al [16] introduced the critical embedment depth Dl of a rigid retaining wall in granular soils under unsaturated conditions. The hydrostatic suction as a linear distribution was adopted. Table 1 lists the physical and strength parameters of silty sand, in which the suction angle φb is a small constant determined via arctan(Sr×tanφ′), and Sr is the degree of saturation. Two different excavation depths H (e.g., 4 and 6 m) were considered. the M-C criterion did not reflect the intermediate principal stress and strength nonlinearity was considered by a small stable suction angle in Ref. [16]. comparisons between the results of AMABILE et al [16] and Eq. (20) of this study with the parameter b=0 and the suction angle φb=18.0o are shown in Fig. 4. Because the soils below the water table are considered saturated, a null matric suction is given in the calculations of earth pressures and moments for this condition.
Table 1 Physical and strength parameters of silty sand [16]

It is indicated from Fig. 4 that the results from Eq. (20) of this study are reasonably consistent with those of AMABILE et al [16]. Therefore, these comparisons confirm the validity of the results proposed in this study to accomplish the overturning design of a rigid retaining wall in unsaturated soils. Note that the results of Eq. (20) are somewhat larger than those of AMABILE et al [16]. This is because the lower bound theorem of plasticity taken by AMABILE et al [16] yields the smallest value of a real answer. Figure 4 also shows that as the water table Dw deepens, smaller embedment depths are demanded to ensure the overturning stability of retaining walls. What is more, a retaining wall is not necessary if the water table is sufficiently deep.

Fig. 4 Comparisons between this study with Eq. (20) and AMABILE et al [16]:
4 Parametric studies
For conformity and convenience in engineering applications, a critical buried coefficient hD of a rigid retaining wall in a foundation pit regarded as an indicator is proposed to analyze and apply the results of this work. The critical buried coefficient hD is defined as
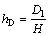 (21)
(21)
From Eq. (21), it is noted that the physical meaning of the critical buried coefficient hD of the retaining wall is the ratio of the critical embedment depth Dl against overturning to the excavation depth H of the foundation pit (i.e., the proportionality coefficient of the critical embedment depth Dl against overturning to the excavation depth H). Accordingly, the critical buried coefficient hD has a specific physical meaning. Moreover, the critical buried coefficient hD is a dimensionless and comprehensive evaluation index and can be able to represent influence characteristics of various parameters. Thus, it also has good comparability and uniformity.
In this section, influence characteristics of the intermediate principal stress, matric suction and its distribution and strength nonlinearity on the critical buried coefficient hD of rigid retaining walls for a foundation pit in unsaturated soils are mainly discussed. A foundation pit with the excavation depth H of 6 m is considered. The water table Dw is assumed to be at 15 m below the ground surface. The unit weight γ of an unsaturated uniform soil is 18 kN/m3. The effective angle of internal friction φ′ and effective cohesion c′ are 20° and 3 kPa, respectively.
What is need to be known that, there are two methods to deal with strength nonlinearity of unsaturated soils [1, 12]: Method I, in which the shear strength versus matric suction is linear and the suction angle φb is a small stable angle; and Method II, in which the shear strength versus matric suction is nonlinear and the suction angle φb changes as the hyperbolic model of Eq. (3b) once matric suction is greater than the air-entry value (ua-uw)b. In the following discussions, Method I is used to investigate the influence of intermediate principal stress and matric suction, in which a small stable suction angle φb of 15°is adopted [1, 12]. Then, the differences between Method I and Method II are discussed at length through the influence of strength nonlinearity.
4.1 Intermediate principal stress
The value of parameter b is between 0 and 1 [24-25]. The greater the parameter b is, the greater the intermediate principal stress effect is. Additionally, different values of parameter b represent different failure criteria. The critical buried coefficient hD versus parameter b is shown in Fig. 5, where UD and LD represent an uniform distribution and a linear distribution of matric suction, respectively.
Figure 5 shows that the critical buried coefficient hD declines with increasing parameter b. The parameter b=0 yields the highest critical buried coefficient, while parameter b=1 yields the lowest one. When matric suction is distributed uniformly with depth, the critical buried coefficients hD with (ua-uw)=50, 25 and 0 kPa of parameter b=1 are decreased respectively by 48.4%, 35.4% and 26.3% comparing to that of parameter b=0. When matric suction is distributed linearly with depth,the critical buried coefficients hD with (ua-uw)o=50, 25 and 0 kPa of parameter b=1 decrease respectively by 40.5%, 32.5% and 26.3% comparing to that of parameter b=0. This indicates that, no matter what matric suction distributes uniformly or linearly with depth, the overturning design for rigid retaining walls of foundation pits in unsaturated soils is obviously affected by choosing a rational failure criterion; moreover, this failure criterion effect for linear suction is not as significant as that for uniform suction. The critical buried coefficient hD based on the M-C criterion with parameter b=0 is over-conservative. More strength potentialities of unsaturated soils are brought due to considering the effect of intermediate principal stress. These can be favorable to understand self-bearing capacity of unsaturated soils objectively and could make engineering design more economical, particularly for (ua-uw)=50 kPa and (ua-uw)o=50 kPa.

Fig. 5 Effect of intermediate principal stress on critical buried coefficient hD:
In addition, the curves of the critical buried coefficient hD versus parameter b are nearly parallel to each other for different (surface) matric suctions. Under the same condition, the critical buried coefficient hD of linear suction is greater than that of uniform suction. As a result, a larger embedment depth is required with linear suction to maintain the overturning stability of a rigid retaining wall.
4.2 Matric suction
Matric suction is the basic nature of unsaturated soils different from saturated soils [1-2]. If matric suction of a soil is zero, it means that this soil is fully saturated. Figure 6 presents the critical buried coefficient hD versus matric suction for three values of parameter b (0, 0.5 and 1).
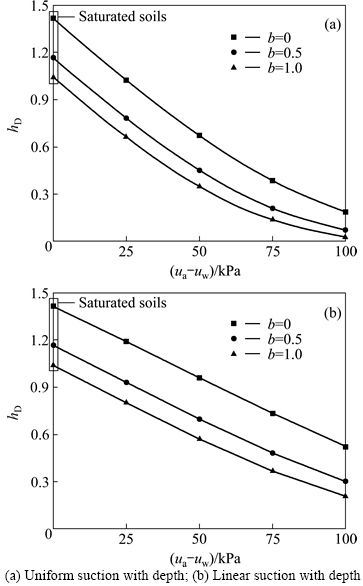
Fig. 6 Effect of matric suction on critical buried coefficient hD:
As shown in Fig. 6, the critical buried coefficient hD declines and even approximates zero with the increase of (surface) matric suction, especially for parameter b=1 and (ua-uw)=100 kPa of uniform suction. When (surface) matric suction is 100 kPa, the critical embedment depths Dl of unsaturated soils with parameter b=0, 0.5 and 1 can be respectively reduced by 7.98, 6.60 and 6.06 m for uniform suction, and 5.34, 5.22 and 4.98 m for linear suction, in comparison to those of saturated soils with null matric suction. It can be concluded that the overturning design of a retaining wall using the saturated soil mechanics is also over-conservative. A great deal of engineering cost would be saved by considering the unsaturated characteristics of soil strength. Some appropriate precautionary measures, such as ground covering, drainage and surface hardening, should be implemented to ensure stable maintenance of matric suction.
The principal differences shown by comparing Figs. 6(a) and (b) are that the critical buried coefficient hD declines nonlinearly with surface suction and is nearly parallel to each other under different values of parameter b; the effect of linear suction with depth is not as remarkable as that of uniform suction with depth. Specific distributions of matric suction in engineering practice should be reasonably assumed.
4.3 Strength nonlinearity
Drawn from sections 4.1 and 4.2, the result of matric suction distributing linearly is similar to that of uniform suction, meanwhile its influence extent is smaller. Therefore, only matric suction distributing uniformly with depth is considered in this section. The air-entry values of unsaturated soils in engineering practice are commonly in the range of 0-50 kPa [1-2], and the average value of 25 kPa (i.e. (ua-uw)b=25 kPa) is taken for discussion. Other conditions are referred to previous data. Figure 7(a) presents the critical buried coefficient hD versus matric suction corresponding to Method I, namely, the suction angle φb takes a small stable angle of 15°; whereas, Figs. 7(b)-(d) show the critical buried coefficient hD versus matric suction corresponding to Method II. For Method II, when (ua-uw)≤(ua-uw)b=25 kPa, the suction angle is equal to the effective angle of internal friction that is φb=φ′=20°; once (ua-uw)>(ua-uw)b=25 kPa, the suction angle φb changes with the hyperbolic model of Eq. (3b). At the same time, the slope n is obtained as 0.0556 by substituting the effective angle of internal friction φ′ into Eq. (4). Three values of the intercept m (0, 5 and 30 kPa) are selected to represent different change rates of the suction angle under high suction for different types of soils. Parameter b takes three values (0, 0.5 and 1) in both Method I and Method II, which corresponds to three orderly series results based on the M-C criterion, a new failure criterion and the twin-shear stress criterion, respectively.
Figure 7(a) indicates that, at the point of the air-entry value (ua-uw)b=25 kPa, the results of Method I are consistent without any jump or inflection points. From Figs. 7(b)-(d), it can be seen that the results of Method II present jump points for m=0 or inflection points for m>0; the critical buried coefficient hD versus matric suction is divided into two distinctly different segments: when (ua-uw)≤(ua-uw)b=25 kPa, the results correspond to the left linear segment and are independent of the parameter m; once (ua-uw)>(ua-uw)b=25 kPa, the results are closely related to the parameter m. In Fig. 7(b) with parameter m=0, the suction angle φb computed by Eqs. (3) and (4) in the whole high suction range is always equal to (φ′-1/n)=2.4598-0.0225φ′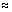 2.0°, which is approximately one-tenth of the suction angle of 20° in low suction range. Therefore, the critical buried coefficient hD presents remarkable jumps at the point of (ua-uw)=(ua-uw)b=25 kPa, and then the critical buried coefficient hD changes very slight. In engineering practices, there are very rare soils suitable for this case. In Figs. 7(c) and (d) with parameter m>0, some inflection points at the air-entry value are brought out, corresponding to different changes of the critical buried coefficient hD on the two sides, and the smaller the parameter m is, the greater the difference is.
2.0°, which is approximately one-tenth of the suction angle of 20° in low suction range. Therefore, the critical buried coefficient hD presents remarkable jumps at the point of (ua-uw)=(ua-uw)b=25 kPa, and then the critical buried coefficient hD changes very slight. In engineering practices, there are very rare soils suitable for this case. In Figs. 7(c) and (d) with parameter m>0, some inflection points at the air-entry value are brought out, corresponding to different changes of the critical buried coefficient hD on the two sides, and the smaller the parameter m is, the greater the difference is.
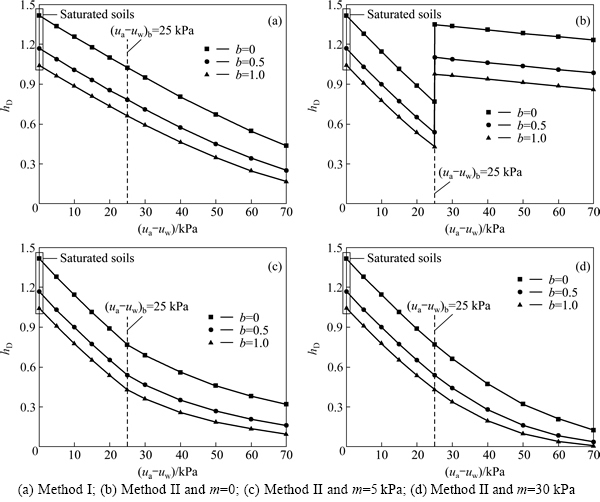
Fig. 7 Effect of strength nonlinearity on critical buried coefficient hD:
As a matter of fact, the right part of these curves in Figs. 7(c) and (d) represents that matric suction has dual-effects on the strength of unsaturated soils (i.e., the strengthening effect with the increase of matric suction and the reducing effect by decreasing the suction angle φb). All of the calculations in this section are that: the strengthening effect by increasing matric suction is greater than the reducing effect by decreasing suction angle. With the increase of matric suction, the critical buried coefficient hD is reducing but the reducing rate becomes more and more slight. This observation provides that the reducing effect by decreasing suction angle is increasing and would approximate the strengthening effect.
Under the same condition, the critical buried coefficient hD of Method I in Fig. 7(a) is greater than that of Method II in Figs. 7(c) and (d). Therefore, Method I is very convenient but conservative for engineering applications. Conversely, Method II is somewhat complicated but consistent with nonlinear strength of unsaturated soils. Under different values of parameter b, there is a great difference between the critical buried coefficients hD obtained both by Method I and Method II. The greater the parameter b is, the more obvious the nonlinear variation of the critical buried coefficient hD is. The assumption of parameter b as 0.5 yields an intermediate critical buried coefficient compared to the highest one of b=0 and the lowest one of b=1. Hence, the effect of intermediate principal stress that is choosing a rational failure criterion is very important for engineering applications.
5 Conclusions
1) Closed-form equations of the critical embedment depth against overturning for a rigid retaining wall of foundation pits in unsaturated soils derived in this work are two sets of orderly new solutions, which could be applied to various engineering conditions and have wide theoretical significance as well as good applicability. The traditional overturning design based on the Mohr-Coulomb criterion is one special case of that with parameter b=0. When matric suction is set to zero, the proposed result degrades to those for saturated soils.
2) The slope of the transformed hyperbolic model of suction angle can be directly identified from the effective angle of internal friction with a favorably fitting linear relationship, and then the intercept could be obtained by less test data with higher accuracy. The newly defined critical buried coefficient with clear physical meanings is a dimensionless and comprehensive evaluation index, and parametric studies regarding it as an index have good comparability and uniformity.
3) The effect of intermediate principal stress on the overturning design of rigid retaining walls in unsaturated soils is remarkable, and with the increase of parameter b, the critical buried coefficient declines. The result with parameter b=0 based on the Mohr-Coulomb criterion is over-conservative. The significant differences in the results with different values of parameter b are a clear indication that the intermediate principal stress effect should be rationally considered to achieve more strength potentials of unsaturated soils and to make the overturning design more economical.
4) The effect of matric suction and its distribution on the critical buried coefficient is significant, and the effect of linear suction is not as remarkable as that of uniform suction. The heights of retaining walls could be reduced or even a retaining wall is not required by considering matric suction. The overturning design of retaining walls based on the saturated soil mechanics would result in great waste. Some appropriate precautionary measures should be implemented to ensure stable maintenance of matric suction.
5) Two methods can address the effect of strength nonlinearity on the overturning stability in unsaturated soils. Method I with a small stable suction angle is simple but conservative, while Method II with a piecewise hyperbolic model of suction angle is precise but slightly complicated. The critical buried coefficient versus matric suction in Method II is strongly influenced by the intercept m. The dual-effects of high suction on the unsaturated soil strength and thus on its structural design should be correctly understood.
References
[1] FREDLUND D G, RAHARDJO H. Soil mechanics for unsaturated soils [M]. New York: John Wiley and Sons, 1993.
[2] LU Ning, LIKOS W J. Unsaturated soil mechanics [M]. New York: John Wiley and Sons, 2004.
[3] YU Mao-hong. Advance in strength theories of materials under the complex stress state in the 20th Century [J]. Applied Mechanics Reviews, 2002, 55(3): 169-218.
[4] MACARI E J, HOYOS L R. Mechanical behavior of an unsaturated soil under multi-axial stress states [J]. Geotechnical Testing Journal, 2001, 24(1): 14-22.
[5] MATSUOKA H, SUN De-an, KOGANE A, FUKUZAWA N, ICHIHARA W. Stress-strain behaviour of unsaturated soil in true triaxial tests [J]. Canadian Geotechnical Journal, 2002, 39(3): 608-619.
[6] HOYOS L R, PEREZ-RUIZ D D, PUPPALA A J. Refined true triaxial apparatus for testing unsaturated soils under suction-controlled stress paths [J]. International Journal of Geomechanics, 2012, 12(3): 281-291.
[7] FREDLUND D G, MORGENSTEM N R, WIDGER R A. The shear strength of unsaturated soils [J]. Canadian Geotechnical Journal, 1978, 15(3): 313-321.
[8] ESCARIO V, SAEZ J. The shear strength of partly saturated soils [J]. Geotechnique, 1986, 36(3): 453-456.
[9] RASSAM D W, COOK F. Predicting the shear strength envelope of unsaturated soils [J]. Geotechnical Testing Journal, 2002, 25(2): 215-220.
[10] HOUSTON S L, PEREZ-GARCIA N, HOUSTON W N. Shear strength and shear-induced volume change behavior of unsaturated soils from a triaxial test program [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11): 1619-1632.
[11] SHENG Dai-chao, ZHOU An-nan, FREDLUND D G. Shear strength criteria for unsaturated soils [J]. Geotechnical and Geological Engineering, 2011, 29(2): 145-159.
[12] ZHANG Lu-lu, FREDLUND D G, FREDLUND M D, WILSON G W. Modeling the unsaturated soil zone in slope stability analysis [J]. Canadian Geotechnical Journal, 2014, 51(12): 1384-1398.
[13] TERZAGHI K, PECK R.B. Soil mechanics in engineering practice (2nd ed.) [M]. New York: John Wiley and Sons, 1967.
[14] HAMID T B, TAWFIK E F. Deep excavation retaining systems in unsaturated soils [C]// Proceedings of the 10th International Conference on Piling and Deep Foundations. Amsterdam, NH, 2006: 135-143.
[15] TAWFIK E, HAMID T, AGGOUR M. Design of cantilever retaining walls in unsaturated soils using AASHTO load and resistance factor design (LRFD) method [C]// Proceedings of the Probabilistic Applications in Geotechnical Engineering. Denver, Colorado, USA, 2007: 1-10.
[16] AMABILE A, BALZANO B, URCIUOLI G, TARANTINO A. Effect of partial saturation on the stability of retaining diaphragms above the water table [C]// Proceedings of the 2nd European Conference on Unsaturated Soils. Naples, Italy, 2012: 263-268.
[17] LI Shun-qun, ZHENG Gang, WANG Ying-hong. Influence of earth berm on retaining structure for unsaturated pit excavation [J]. Engineering Mechanics, 2012, 29(5): 122-127. (in Chinese)
[18] STANIER S A, TARANTINO A. An approach for predicting the stability of vertical cuts in cohesionless soils above the water table [J]. Engineering Geology, 2013, 158: 98-108.
[19] TARANTINO A, MOUNTASSIR G E. Making unsaturated soil mechanics accessible for engineers: preliminary hydraulic-mechanical characterization & stability assessment [J]. Engineering Geology, 2013, 165: 89-104.
[20] VO T, RUSSELL A R. Unsaturated soil interacting with a rotating model wall [J]. International Journal of Physical Modelling in Geotechnics, 2013, 13(2): 63-78.
[21] VO T, RUSSELL A R. Slip line theory applied to a retaining wall-unsaturated soil interaction problem [J]. Computers and Geotechnics, 2014, 55: 416-428.
[22] ZHANG Chang-guang, ZHAO Jun-hai, ZHANG Qing-he, XU fei. Unified solutions for unsaturated soil shear strength and active earth pressure [C]// Proceedings of the GeoShanghai 2010-Experimental and Applied Modeling of Unsaturated Soils (GSP 202). Shanghai, China, 2010: 218-224.
[23] ZHANG Chang-guang, HU Yun-shi, ZHAO Jun-hai. Unified solution of shear strength for unsaturated soil under plane strain condition and its application [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(1): 32-37. (in Chinese)
[24] YU Mao-hong, YANG Song-yan, Fan San-cheong, MA Guo-wei. Unified elasto-plastic associated and non-associated constitutive model and its engineering applications [J]. Computers and Structures, 1999, 71(6): 627-636.
[25] YU Mao-hong. Unified strength theory and its applications [M]. Berlin, Heidelberg: Springer & Verlag, 2004.
[26] ZHANG Chang-guang, ZHU Dong-hui, GAO Zhi, XUE Guang-wei, LI Zheng. Unified solution of passive earth pressure for unsaturated soils [C]// Proceedings of the 2012 Global Conference on Civil, Structural and Environmental Engineering. Yichang, China, 2012: 430-433.
(Edited by YANG Hua)
Foundation item: Project(41202191) supported by the National Natural Science Foundation of China; Project(2015JM4146) supported by the Natural Science Foundation of Shaanxi Province, China; Project(2015) supported by the Postdoctoral Research Project of Shaanxi Province, China
Received date: 2015-04-08; Accepted date: 2015-07-22
Corresponding author: ZHANG Chang-guang, Associate Professor, PhD; Tel: +86-29-82337238; E-mail: zcg1016@163.com
Abstract: The overturning stability is vital for the retaining wall design of foundation pits, where the surrounding soils are usually unsaturated due to water draining. Moreover, the intermediate principal stress does affect the unsaturated soil strength; meanwhile, the relationship between the unsaturated soil strength and matric suction is nonlinear. This work is to present closed-form equations of critical embedment depth for a rigid retaining wall against overturning by means of moment equilibrium. Matric suction is considered to be distributed uniformly and linearly with depth. The unified shear strength formulation for unsaturated soils under the plane strain condition is adopted to characterize the intermediate principal stress effect, and strength nonlinearity is described by a hyperbolic model of suction angle. The result obtained is orderly series solutions rather than one specific answer; thus, it has wide theoretical significance and good applicability. The validity of this present work is demonstrated by comparing it with a lower bound solution. The traditional overturning designs for rigid retaining walls, in which the saturated soil mechanics neglecting matric suction or the unsaturated soil mechanics based on the Mohr-Coulomb criterion are employed, are special cases of the proposed result. Parametric studies about the intermediate principal stress, matric suction and its distributions along with two strength nonlinearity methods on a new defined critical buried coefficient are discussed.


