Trans. Nonferrous Met. Soc. China 20(2010) s774-s780

Experimental studies and phase field modeling of microstructure evolution during solidification with electromagnetic stirring
P. Gerald Tennyson1, P. Kumar2, H. Lakshmi2, G. Phanikumar1, P. Dutta2
1. Department of Metallurgical and Materials Engineering, Indian Institute of Technology, Madras 600036, India;
2. National Facility for Semisolid Forming, Department of Mechanical Engineering, Indian Institute of Science,
Bangalore 560012, India
Received 13 May 2010, accepted 12 July 2010
Abstract:
Thixocasting requires manufacturing of billets with non-dendritic microstructure. Aluminum alloy A356 billets were produced by rheocasting in a mould placed inside a linear electromagnetic stirrer. Subsequent heat treatment was used to produce a transition from rosette to globular microstructure. The current and the duration of stirring were explored as control parameters. Simultaneous induction heating of the billet during stirring was quantified using experimentally determined thermal profiles. The effect of processing parameters on the dendrite fragmentation was discussed. Corresponding computational modeling of the process was performed using phase-field modeling of alloy solidification in order to gain insight into the process of morphological changes of a solid during this process. A non-isothermal alloy solidification model was used for simulations. The morphological evolution under such imposed thermal cycles was simulated and compared with experimentally determined one. Suitable scaling using the thermosolutal diffusion distances was used to overcome computational difficulties in quantitative comparison at system scale. The results were interpreted in the light of existing theories of microstructure refinement and globularisation.
Key words:
electromagnetic stirring; non-dendritic; phase field modeling; microstructure;
1 Introduction
Dendritic solidification has been an important aspect of solidification research for many decades. These microstructures which are formed during solidification of metals and alloys result from the morphological instabilities at the solid-liquid interface. The growing dendrites form a continuous skeleton in the liquid-solid zone and a considerable effort is required to change this pattern through mechanical deformation or heat treatment. Rheocasting is a novel technique where metallic alloy is subjected to shear in its mushy state during solidification to create a globular/spheroidal microstructure as opposed to dendritic microstructure[1]. In this study, an attempt is made to understand the dendrite fragmentation and evolution of a fine globular microstructure that takes place during a semi-solid processing technique such as electromagnetic stirring in a rheocasting setup.
The physical phenomena that take place during the process of dendrite fragmentation are many and several experimental studies, in-situ visualization and simulation studies have come into the open literature in the recent past. It is believed that the root of the dendrite arm (primary/secondary etc) plays an important role in the fragmentation process. Many theories have been put forward to explain the fragmentation of the dendrites, of which one is the remelting of the dendritic arms at its roots by thermal gradients and solute enrichment at the roots. JACKSON et al[2] explained that remelting can be caused by partial melting of the dendrites because of the interaction of the two diffusion fluxes namely thermal and solutal fluxes. As more amount of solute gets enriched near the roots, the original solidus temperature of the solidifying structure will be increased, and due to high solute content, necking at the branches will occur. KATTAMIS et al[3] explained that remelting can possibly occur when there is a solutal influx towards regions of less radius, i.e. the neck from regions of large radius that are solute rich. FAN[4] pointed out that spheroidisation of individual particles after remelting will happen due to atomic flux from areas of high curvature to areas of low curvature. RUVALCABA et al[5] showed that local fragmentation of the tertiary arms can be caused by incoming solute rich liquid flow. MATHIESEN et al[6] showed that dendrite fragmenta- tion occurs not only by solute driven flow but also by the buoyant transport of the solvent to the front. These fragments get carried away by the flow and get piled up and will further enhance the fragmentation process.
In order to gain a physical insight into the process described above, an appropriate computational model may be necessary. Phase field models are a recent class of models that have been widely used to compute the solidification morphologies in order to avoid explicit tracking of the interfaces. The phase field technique has been applied to many different situations of microstructure evolution and the subject has been reviewed fairly extensively[7-10]. By introducing an auxiliary variable, the phase field, that characterizes the physical state (liquid or solid) of the system at each point and its governing equation, one can employ numerical schemes that avoid interface tracking. WHEELER et al [11] introduced a phase field model for binary alloy solidification in the isothermal limit. WARREN and BOETTINGER[12] developed the model using an entropy formulation. In this work, a phase field model based on the WHEELER’s model is employed to study the effect of remelting on the dendrite fragmentation.
2 Experimental results
The alloy system chosen for this study is Al-7Si-0.3Mg alloy as shown in the section of phase diagram in Fig.1. The details of linear electromagnetic stirring setup developed with a rheocasting unit have been presented elsewhere[13-16] along with experimental results with parametric variation. To illustrate the globularization phenomena, we choose to present here results for electromagnetic stirring with 250 A and 50 Hz. Microstructures of the ingot from the top to the bottom are shown in Fig.2. The temperature of the melt in the mould at various heights was measured using thermocouples positioned as shown in Fig.3(a). As can be seen from the temperature profiles in Fig.3(b), there is a vertical thermal gradient in the melt. Ingots are solidified by extracting heat at the bottom of the rheocasting setup leading to the ingots being nearly 30 cm long and having effectively undergone directional solidification in the presence of electromagnetic stirring. There is a gradient in the microstructure from the outer edge to the centre of the ingot, but it is not significant enough when compared wiht an ingot stirred at different current. As can be noted, with the progress of solidification towards the top of the billet, the microstructure becomes increasingly globular. The electromagnetic field in the mould is modeled using MagNet? software and the resultant forced convection is modeled using CFD software FLUENT. Typical results are given in Fig.4 . As can be noted, there is a vortex that makes the fluid circulate between the colder bottom region and the hotter top region within the mould.
It is well established that in a directional solidification setup, there is a layer of free floating dendrites just above the mushy zone. One can assume that the thermal profile experienced by a dendrite advected by the forced convection present in the mould would fluctuate between two values: a lower temperature when the dendrite is close to the bottom of the melt and a higher temperature when the dendrite is far away from the solid-liquid interface. A more precise approach would be to take a Lagrangian approach by tracking the dendrite within the melt and applying the thermal conditions as experienced by it during the forced convection. However, it is believed that modeling this process using a two step thermal profile will capture the essential phenomenon, leading to dendrite fragmentation by remelting at dendrite roots as illustrated by the simulation studies that follow this section.
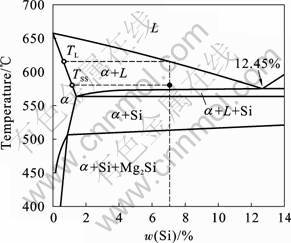
Fig.1 Section of Al-Si-Mg phase diagram indicating alloy chosen for this study[17]
3 Model
The model employed for this study is the isothermal binary alloy solidification model as developed by WHEELER et al[11]. It uses a phase field variable Φ, which is 0 in the liquid and 1 in the solid and varies smoothly between these bulk values within the diffuse interface region.
The anisotropic form of the phase field is given as:
![]() (1)
(1)
and the concentration field is given by
![]()
![]() (2)
(2)
Anisotropy is included in the system as
![]() (3)
(3)
where γ is the strength of anisotropy, k is the mode number (as in two fold or four fold anisotropy) and θ = arctan(![]() y/
y/![]() x)
x)
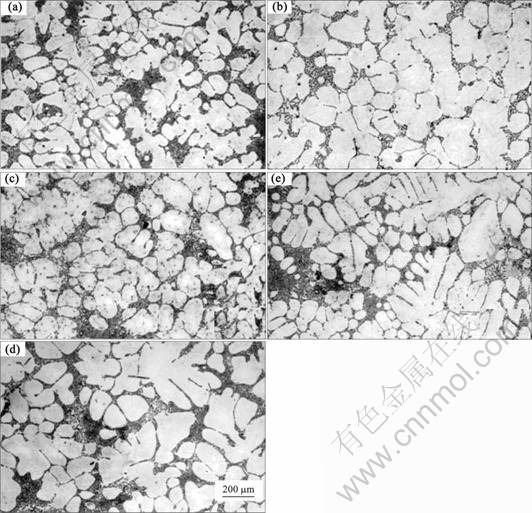
Fig 3. Optical micrographs of samples at different depths from top surface of billet (EM stirring with 250 A current at 50 Hz): (a) 100 mm; (b) 200 mm; (c) 300 mm; (d) 400 mm; (e) 500mm
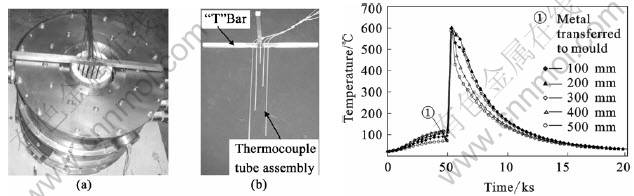
Fig.3 Position of thermocouples in mould (a, b) and thermal profile (c) measured by thermocouples at different heights[13]
The homogenous free energy density is given by
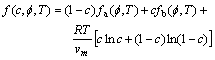 (4)
(4)
where fa and fb are the free energy densities of the pure components.
![]() (5)
(5)
![]() (6)
(6)
![]() ,
, ![]()
Mf and Mc as referenced in Eq.(1) are phase field and concentration mobilities, respectively. The free energy densities chosen are that the corresponding phase diagram will be a lens shaped one as shown in Fig.5 as suitable for the primary solidification stage of the actual alloy system. The labels b, c and d for temperatures in Fig.6 correspond to those in Fig.5.
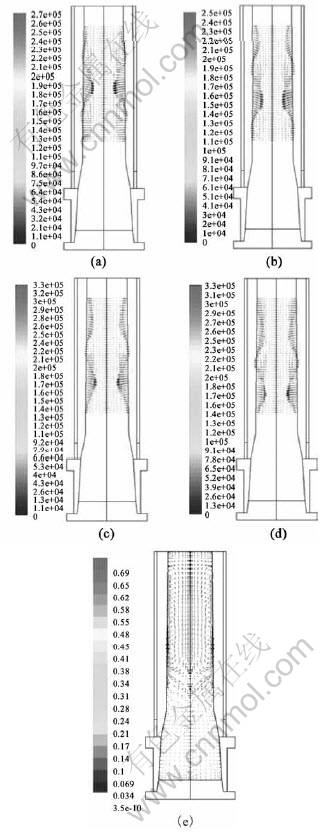
Fig.4 Electromagnetic field distribution along radial and axial directions at t=0.04 s (a), t=0.08 s (b), t=0.12 s (c), t=0.16 s (d) and resultant convection pattern (e) in liquid metal in mould for case of stirring with current 250 A at 50 Hz
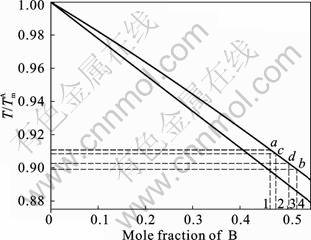
Fig.5 A simple lens type phase diagram
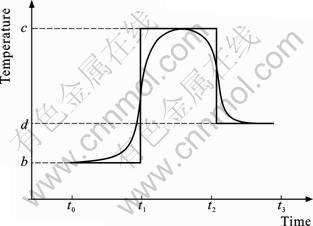
Fig.6 Temperature time profile used for simulation, where b, c and d are from phase diagram in Fig.5
Fig.7 shows a schematic of the rheocasting mould and the forced convection pattern due to electromagnetic stirring. Superimposed on a stream line is a schematic of how a free floating dendrite would experience the surrounding temperature field (higher temperature at top and lower at bottom of the mould). The thermal profile that such a free floating dendrite would experience is modeled as a two stage cycle shown in Fig.6.
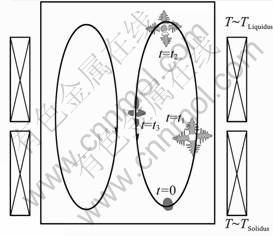
Fig.7 Model of free dendrite advection due to forced convection in melt due to electromagnetic stirring (The labels correspond to stages shown in x-axis of Fig.6)
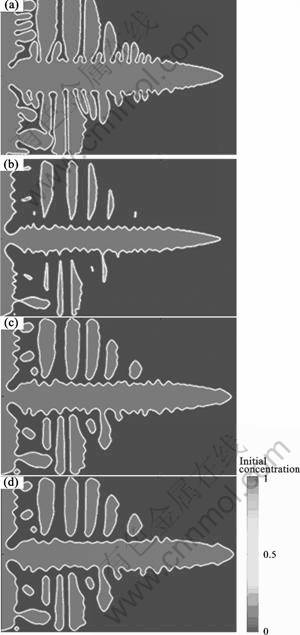
Fig.8 Phase field simulation of dendritic to globular transition: (a) Fully developed dendrite; (b) Remelting of dendrite at position c from Fig.5; (c, d) Solidifying at lower temperature at position d from Fig.5 (onset of globularisation)
4 Numerical simulations
The equations given above were solved using an explicit finite difference technique. All the simulations were performed on a rectangular domain with a 1500×1000 grid system. The temperature was non- dimensionalized with melting point of one of the components. A simple lens type phase diagram was taken for the study as shown in Fig.5. For numerical stability Δt ≤ Δx2/DL was considered, where Δt is the time step size used for the calculations, Δx the grid size and DL the diffusivity of the solute in the liquid.
No flux conditions (Neumann boundary conditions) at the boundaries were applied both for phase and concentration fields. A square seed was nucleated at the left boundary of the domain where the initial concentration of the melt was 1 at the liquidus temperature denoted by point a. The melt is initially undercooled to 20 K below the liquidus temperature to b as shown in Fig.5. Due to undercooling, the dendrite starts to evolve and after a few time steps, when the dendrite has traversed the domain, the temperature of the whole domain is now increased to point c (4 K below the liquidus) and held for a duration sufficient to allow for the remelting process to be significant. It is possible to perform detailed calibration studies to tune this holding time to represent the effective time spent by the dendrite at a given temperature environment using the actual thermal profile at the location of the freely floating dendrite by integrating the calculated velocities. However, in this study, we choose to illustrate the solute segregation induced remelting qualitatively. Root remelting occurs at this higher temperature and the secondary arms get detached from the primary dendrite. The local concentration now tries to stabilize to the equilibrium concentration at point c. After holding at c, the temperature of the domain is now decreased to point d (14 K below liquidus) and held for a similar duration as in the heating stage. During this stage, the fragments grow in a globular manner. The temperature profile for the whole simulation is shown in Fig.6.
5 Discussion
The phase diagram in Fig.5 shows that the initial concentration of the melt is at 1, which corresponds to 0.463 mole fraction of B. As the melt is solidified at 20 K below the liquidus temperature, the equilibrium concentration at point b is found to be 0.52. Hence in Fig.9, we can see that the local equilibrium concentration between the solid and the liquid is 0.52 whereas the far field composition is still at 0.463. Now, when the temperature of the melt is suddenly increased to point c, the solute concentration prevailing between the secondary arm roots is now at a much higher concentration as opposed to the equilibrium concentration of 0.474. As a result of this higher concentration, the secondary arm roots start to disengage themselves from the primary stem. The temperature is then decreased to point d, which causes the pinched off arms to coarsen. Globularization of individual fragments now occurs due to solute flux from areas of high curvature to areas of low curvature, which is evident from Fig.10(b) and Fig.8(c) according to FAN[4]. Incorporating convection in the melt will cause the individual fragments to be transported and get solidified as globules.
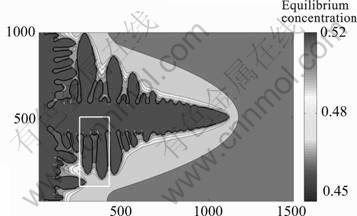
Fig.9 Fully grown dendrite with primary and secondary arms shown using concentration map (The box in white shows inset of two side arms that will melt during heating)

Fig.10 Evolution composition profile (a,b,c) of side arms shown in inset of Fig.9 during heating stage; evolution of phase field (d,e,f) of side arms as shown in inset of Fig.9 with increasing time during heating stage (All shades of red/brown correspond to solid regions and those of blue correspond to liquid regions)
From Fig.10 we can conclude that the pinch-off of side arms takes place due to melting at the root induced by a lower liquidus at the local composition as corroborated experimentally in another system using direct visualization experiments[5]. It is well established that the segregation of solute is expected at regions of high curvature due to Gibbs-Thomson effect. The root melting observed in the simulation study presented can be attributed to the lower local liquidus temperatures of these regions. As the solidification proceeds from the bottom of the ingot towards the top, more and more such dendrite fragmentation is expected to take place, leading to finer and more globular microstructure. This is corroborated by a more globular microstructure at the top of the ingot as shown in Fig.2.
6 Conclusions
A phase field model for solidification was used to demonstrate the effect of dendrite fragmentation in a binary alloy. The globularization phenomenon was captured effectively by modeling the thermal profile experienced by a free floating dendrite due to forced convection during linear electromagnetic stirring in a typical rheocasting setup. Finer and more globular microstructure that results towards the end of a directional solidification in a rheocasting setup in the presence of electromagnetic stirring could be explained by a repeated process of root melting in free floating dendrites induced by fluctuating thermal conditions.
References
[1] FELMINGS M C. Behavior of metal alloys in semi-solid state[J]. Metallurgical Transactions A,1991, 22: 957-981.
[2] JACKSON K, HUNT J, UHLMANN D, SEWARD T. On the origin of the equiaxed zone in castings[J]. Trans AIME, 1966, 236: 149-157.
[3] Kattamis T Z, Coughlin J C, Flemings M C. Influence of coarsening of dendrite arm spacing of aluminum- copper alloys[J]. Trans AIME, 1967, 239: 1504-11.
[4] FAN Z. Semisolid metal processing[J]. International Materials Reviews, 2002, 47: 49-85.
[5] Ruvalcaba D, Mathiesen R H, Eskin D G, Arnberg L, Katgerman L. In situ observation of dendrite fragmentation due to local solute-enrichment during directional solidification of an aluminium alloy[J]. Acta Materialia, 2007, 55: 4287-4292.
[6] Mathiesen R H, Arnberg L, Bleuet P, Somogyi A. Crystal fragmentation and columnar to equiaxed transitions in Al-Cu studied by synchrotron X-ray video microscopy[J]. Metall Mater Trans A, 2006, 37: 2515-2524.
[7] KARMA A. Phase field methods [M]//Encyclopedia of Materials Science and Technology. Oxford, UK: Elsevier, 2001: 6873-6886.
[8] CHEN Long-qing. Phase field models for microstructure evolution[J]. Annual Review of Materials Research, 2002, 32: 113-140
[9] HOYT J J, ASTA M,KARMA A. Atomistic and continuum modeling of dendritic solidification[J]. Materials Science and Engineering R,2003, 41(6): 121-163.
[10] MOELANS N, BLANPAIN B, WOLLANTS P. An introduction to phase-field modelling of microstructure evolution[J]. Calphad, 2008, 32(2): 268-294.
[11] WHEELER A A, BOETTINGER W J, MCFAADDEN G B. Phase field model for isothermal phase transitions in binary alloys[J]. Physical Review A , 1992, 45:7424-7439.
[12] WARREN J A, BOETTINGER W J. Prediction of dendritic growth and microsegregation patterns in a binary alloy using the phase field method[J]. Acta Metallurgica et Materialia, 1995, 43: 689-703.
[13] KUMAR P. Experimental investigation of Rheocasting usinglinear electromagnetic stirring[D]. Indian Institute of Science, Bangalore, India, 2008.
[14] BARMAN N, KUMAR P, DUTTA P. Studies on transport phenomena during solidification of an aluminum alloy in presence of linear electromagnetic stirring[J]. Journal of Materials Processing Technology, 2009, 209(18/19): 5912-5923.
[15] KUMAR P, LAKSHMI H, DUTTA P. Solidification of A356 alloy in a linear electromagnetic stirrer[J]. Solid State Phenomena, 2008,141/143: 563-568.
[16] KUMAR A,DUTTA P. Modeling of Transport phenomena during continuous casting of non-dendritic billets[J]. international journal of Heat and Mass Transfer, 2005, 48: 3674-3688.
[17] OGRIS E. Development of Al-Si-Mg alloys for semi-solid processing and silicon spheroidization treatment (SST) for Al-Si cast alloys[D]. Swiss Federal Institute of Technology, Zurich, 2002.
(Edited by YUAN Sai-qian)
Corresponding author: G. PHANIKUMAR; E-mail: gphani@iitm.ac.in


