
J. Cent. South Univ. (2021) 28: 1584-1600
DOI: https://doi.org/10.1007/s11771-021-4718-6
A stochastic user equilibrium model solving overlapping path and perfectly rational issues
YAN Dong-mei(闫冬梅), GUO Jian-hua(郭建华)
Intelligent Transportation System Research Center, Southeast University, Nanjing 211189, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract:
Traffic assignment has been recognized as one of the key technologies in supporting transportation planning and operations. To better address the perfectly rational issue of the expected utility theory (EUT) and the overlapping path issue of the multinomial logit (MNL) model that are involved in the traffic assignment process, this paper proposes a cumulative prospect value (CPV)-based generalized nested logit (GNL) stochastic user equilibrium (SUE) model. The proposed model uses CPV to replace the utility value as the path performance within the GNL model framework. An equivalent mathematical model is provided for the proposed CPV-based GNL SUE model, which is solved by the method of successive averages (MSA). The existence and equivalence of the solution are also proved for the equivalent model. To demonstrate the performance of the proposed CPV-based GNL SUE model, three road networks are selected in the empirical test. The results show that the proposed model can jointly deal with the perfectly rational issue and the overlapping path issue, and additionally, the proposed model is shown to be applicable for large road networks.
Key words:
Cite this article as:
YAN Dong-mei, GUO Jian-hua. A stochastic user equilibrium model solving overlapping path and perfectly rational issues [J]. Journal of Central South University, 2021, 28(5): 1584-1600.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-021-4718-61 Introduction
Traffic assignment is one of the significant methods in the studies of transportation science, which has been widely investigated and applied in supporting the generation of policies for transportation planning and operations. Traffic assignment approach is typically used to assign a known origin-destination (O-D) demand to the links in a road network based on route choice model such that the traffic flow of each link can be determined. In this way, the link flow can be used for testing the rationality of road network planning. Additionally, based on the equilibrium traffic flow provided by traffic assignment, the time-space distribution of traffic flows can be manipulated by measures such as traffic signal control or traffic guidance. Thereby the urban traffic congestion is further alleviated.
The stochastic user equilibrium (SUE) model proposed by DAGANZO et al [1] is considered to be a typical method to solve the traffic assignment problem since it provides a reasonable equilibrium traffic flow pattern by considering travelers’ imperfect perceptions of travel cost. Traditionally, the SUE model is constructed usually based on the multinomial logit (MNL) route choice model [2]. It is well known that the MNL model exhibits the property of independence of irrelevant alternatives (IIA), which leads to a failure of the SUE modeling process, i.e., not considering the overlapping path issue.
In reality, the road networks in the real world contain a fairly large number of overlapping paths, so it is essential to consider the overlapping path problem in the SUE modeling process. To this end, many studies have been proposed to deal with the overlapping path problem in the SUE modeling process [3-6]. Note that these studies are all based on the expected utility theory (EUT). It is well known that there are many stochastic factors (e.g., traffic accidents) in the transportation systems. In such uncertain traffic environment, the route choice behavior of the travelers exhibits violations of the EUT [7-10]. In other words, EUT has long been considered inadequate to describe the route choice behavior of the travelers, i.e., EUT inherently has a perfectly rational issue. It can be interpreted in this paper as travelers who are absolutely rational when making route choice decisions [11]. By doing so, it will lead to the EUT-based stochastic user equilibrium model generating unrealistic equilibrium flow patterns.
In SUE modeling, there are also many studies that can deal with the overlapping path problem but do not consider adequately the perfectly rational problem at the same time. Therefore, given the lack of joint investigations into the overlapping path issue and the perfectly rational issue, the objective of this paper is to develop a cumulative prospect value (CPV) based generalized nested logit (GNL) SUE model. In reality, the proposed model changes the utility value (UV) based GNL SUE model presented by BEKHOR et al [3] through replacing the utility values with the cumulative prospect values. For the proposed model, an equivalent mathematical model and an associated solution based on method of successive averages (MSA) are provided. The existence and equivalence of the solution are also proved. Furthermore, a small network and the well-known Nguyen-Dupuis network are selected to test the performance of the proposed CPV-based GNL SUE model in dealing with the overlapping path issue and perfectly rational issue. The Sioux Falls network is also selected to test the applicability of the proposed model in a large road network.
The organization of this paper is as follows. First, the next section provides a literature review on the traffic assignment studies involving the overlapping path issue and the perfectly rational issue. Then, in the following section, the cumulative prospect value (CPV)-based SUE GNL model is proposed. Afterwards, the equivalent mathematical model and the associated MSA solution are provided, followed by the numerical examples to demonstrate the performance of the proposed model. Finally, conclusions of the paper are provided.
2 Literature review
2.1 Overview on overlapping path issue
The route choice model is a key component of traffic assignment, which typically uses the MNL model. It is well known that the MNL model suffers from the IIA deficiency, which leads to a failure of the MNL model in capturing similarities between different paths. In other words, the MNL model naturally has the overlapping path issue. To deal with this issue, DAGANZO et al [1] proposed the multinomial probit (MNP) model with an assumption that the joint density of the random error terms follows multivariate normal function. However, the MNP model suffers from the absence of a closed mathematical form for the choice probabilities, which requires a simulation method to calculate the choice probabilities [12-14]. The same also happens for the mixed logit model [15, 16]. Clearly, a computational issue will arise due to the application of simulation method.
Other discrete choice models can be classified into two categories according to the model structure. The first category is the modifications of MNL model, which addresses the overlapping path problem by adding a correction term to the deterministic part of the utility function. These models still maintain the single-level tree structure of the MNL model, including C-logit model [17-19] and path-size logit (PSL) model [20, 21]. Note that these models cannot capture the proper effect of path correlations in the choice probabilities [14, 15, 22, 23].
The second category is generalized extreme value (GEV) class of models proposed by MCFADDEN [24]. The GEV models can capture the similarity between different paths through the error component in the utility function and adopt a two-level tree structure. These models mainly include nested logit (NL) model [25], paired combinatorial logit (PCL) model [26-28], cross nested logit (CNL) model [4, 5, 29], and generalized nested logit (GNL) model [3, 30]. Note that the NL, PCL and CNL models have restrictions such as the equality of cross elasticities between pairs of alternatives in or not in the common nests, equal proportion of path assignment, and the same nested coefficients. In addition, the GNL model did not consider the perfectly rational issue in modeling the route choice behavior.
2.2 Overview on perfectly rational issue
In earlier studies, route choice behavior modeling is based on expected utility theory (EUT) and random utility theory (RUT). However, these theories assume that travelers have the same preferences, which causes travel route choice behavior to exhibit violations of EUT under the uncertain environment of road networks [7]. Furthermore, EUT assumes that travelers are perfectly rational when making route choice decisions. In reality, however, an individual’s behavior is usually influenced by many factors (e.g., psychological state, environmental elements). Therefore, the prospect theory (PT) proposed by KAHNEMAN et al [31] and cumulative prospect theory (CPT) developed by TVERSKY et al [32] are used to overcome the drawback of the EUT.
Cumulative prospect theory (CPT) has been widely used in route choice modeling for handling the perfect rational issue in traffic assignment. In this end, CONNORS et al [33] modified the traditional user equilibrium (UE) in the context of stochastic link travel time through using the perceived value (PV) instead of the utility value (UV). On this basis, XU et al [9] encapsulated endogenous reference point (RP) into a multiclass prospect-based user equilibrium model. WANG et al [8] extended the model of XU et al [9] to a cumulative prospect theory-based user equilibrium (CPT-UE) model in the context of stochastic link capacity degradation. Along this line, WANG et al [34] considered stochastic perception error (SPE) in the CPT-UE modeling process. Furthermore, YANG et al [11] developed a cumulative prospect theory-based stochastic user equilibrium (CPT-SUE) model. Note that all these models did not consider the overlapping path issue in modeling the route choice behaviors.
2.3 Summary
As mentioned in the introduction section, the overlapping path issue and the perfectly rational issue inherently exist in the SUE models. To this end, the above literature review indicates that many studies have been proposed to deal with these two problems separately, while there is still a need to solve these two problems jointly. Thus, we propose a CPV-based GNL SUE model through using CPV instead of utility value as path performance in the GNL model framework to meet this requirement. In addition, an equivalent mathematical model and an associated solution are provided for the proposed CPV-based GNL SUE model.
3 CPV-based GNL SUE modeling
In this section, we first calculate the CPV in the context of stochastic link capacity degradation. Then, the CPV-based route choice model is provided by using the calculated CPV instead of the utility value as path performance in the GNL model framework. Finally, the CPV-based GNL SUE model is presented through incorporating the SUE condition.
3.1 CPV computation
In order to build the CPV-based route choice model, we must calculate the CPV first. Specifically, we first describe the travel time distributions in the context of stochastic link capacity degradation. Second, we use the minimum travel time budget as the reference point based on the calculated mean and variance of the path travel time. Finally, on the basis of the reference point, the CPV equation of each path is obtained by combing a value function and a probability weighting function.
3.1.1 Travel time distribution
In transportation systems, many uncertain events, such as bad weather or traffic incidents, will cause stochastic link capacity degradations, leading to randomly changing travel times. In this context, this section will describe the travel time distributions as follows.
First, the well-known bureau of public roads (BPR) [35] link performance function is given as Eq. (1).
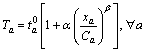 (1)
(1)
where Ta is travel time with link flow xa on link a; 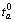 and Ca are the free-flow travel time and capacity on link a, respectively; α and β are deterministic parameters, respectively.
and Ca are the free-flow travel time and capacity on link a, respectively; α and β are deterministic parameters, respectively.
Second, it is assumed that link capacity Ca follows uniform distribution over interval 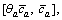 where the upper bound ca is the actual capability, the lower bound
where the upper bound ca is the actual capability, the lower bound is the worst-degraded capability, and θa is a fraction of the design capacity. Note that link travel time Ta is also a random variable due to random variable Ca. According to LO et al [36], the mean and variance of Ta are expressed as Eqs. (2) and (3), respectively.
is the worst-degraded capability, and θa is a fraction of the design capacity. Note that link travel time Ta is also a random variable due to random variable Ca. According to LO et al [36], the mean and variance of Ta are expressed as Eqs. (2) and (3), respectively.
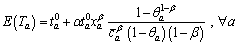 (2)
(2)
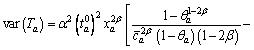
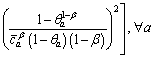 (3)
(3)
Finally, according to the central limit theorem [37], the path travel time follows a normal distribution regardless of the distribution of link travel time. Therefore, the mean and variance of the path travel time are given in Eqs. (4) and (5), respectively as:
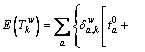
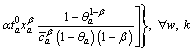 (4)
(4)
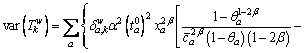
 (5)
(5)
where 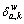 is the relationship between path k and link a;
is the relationship between path k and link a; 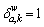 if path k contains link a, and
if path k contains link a, and 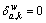 , otherwise.
, otherwise.
3.1.2 Reference point
The reference point (RP) is the expectation of the travelers on travel time during the route choice process, related to usual factors such as traveler experiences or traveling situation. Meanwhile, the RP is also the turning point of risk attitudes of travelers. When the path utility is smaller than the RP, the travelers may avoid risk, i.e., be risk averse. When the path utility is larger than the RP, the traveler could take risk, i.e., be risk seeking. This means that the travelers judge the value of the path based on the difference in path utility relative to the reference point rather than the absolute path utility.
To avoid exogenous inputs of reference points without guidance, we adopt endogenous reference points proposed by XU et al [9], that is
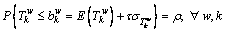 (6)
(6)
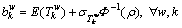 (7)
(7)
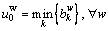 (8)
(8)
where 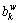 is travel time budget on path k between O-D pair w;
is travel time budget on path k between O-D pair w; 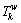 is the travel time on path k between O-D pair w;
is the travel time on path k between O-D pair w; 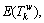 and
and 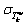 are the mean and standard deviation of
are the mean and standard deviation of 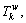 respectively; ρ is on-time arrival probability within the budgeted time; Φ-1 is the inverse function of the standard normal cumulative distribution function;
respectively; ρ is on-time arrival probability within the budgeted time; Φ-1 is the inverse function of the standard normal cumulative distribution function; 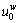 is reference point between O-D pair w; τ is a parameter related to on-time arrival probability.
is reference point between O-D pair w; τ is a parameter related to on-time arrival probability.
3.1.3 CPV equation
In this study, we use CPV instead of the utility value as the path performance in the route choice process. Based on the previously calculated reference point, the CPV is calculated by a value function and a probability weighting function. Note that the value function often exhibits risk aversion over gains and risk seeking over losses, and the probability weighting function often over-weights small probabilities and under-weights the moderate and high probabilities. The value function, the probability weighting function, and the CPV equation are
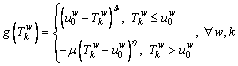 (9)
(9)
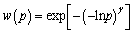 (10)
(10)
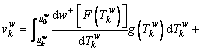
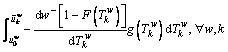 (11)
(11)
where 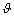 and η measure the degree of diminishing sensitivity of the value function; μ is the loss-aversion coefficient, indicating the value function is steeper for losses than for the same gains; γ measures the degree of distortion of the probability judgment in the decision process. Generally,
and η measure the degree of diminishing sensitivity of the value function; μ is the loss-aversion coefficient, indicating the value function is steeper for losses than for the same gains; γ measures the degree of distortion of the probability judgment in the decision process. Generally,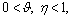 μ≥1, and 0<γ<1. Moreover, w(p) and p are the perceived probability and actual probability of an event, respectively. Note that w(p) increases monotonically with respect to p regardless of the value of γ [38]. In CPV equation,
μ≥1, and 0<γ<1. Moreover, w(p) and p are the perceived probability and actual probability of an event, respectively. Note that w(p) increases monotonically with respect to p regardless of the value of γ [38]. In CPV equation,  and
and 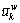 are the lower bound and upper bound of the travel time on path k between O-D pair w, respectively. The lower bound
are the lower bound and upper bound of the travel time on path k between O-D pair w, respectively. The lower bound
 is the free-flow travel time, and the upper bound
is the free-flow travel time, and the upper bound 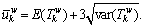
3.2 CPV-based route choice modeling
The route choice model is fundamental in traffic assignment. In this section, to build CPV-based GNL SUE model, we apply CPV instead of the utility value as the path performance to construct the CPV-based route choice model in the GNL model framework.
3.2.1 Perceived CPV of path
The cumulated prospect value (CPV) of each path can be regarded as the sum of the prospect value of each link contained in this path, which is expressed as:
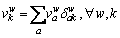 (12)
(12)
Different reference points and familiarity with road network conditions lead to different prospect values of the paths. Consequently, the CPV of the path is a random variable, which contains a deterministic part 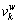 and a random error part
and a random error part 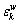 .
.
 (13)
(13)
where 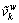 is the perceived CPV of the path;
is the perceived CPV of the path; 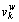 is the actual CPV of the path;
is the actual CPV of the path;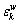 is the random error.
is the random error.
3.2.2 CPV-based route choice model
The traditional GNL model is described as a two-level nesting structure. The upper layer consists of all links (nests) in the network, and the lower layer includes all paths (alternatives) in the network. In this study, we modify the traditional GNL model derived from GEV theory [24] by replacing the utility value with CPV. The probability of choosing path k between O-D pair w is given by:
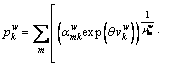
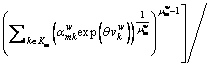
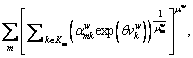
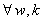 (14)
(14)
where 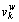 is the cumulative prospect value of path k between O-D pair w; θ is a dispersion parameter, which characterizes the familiarity of a user with the road network; Km is set of all paths included in nest m;
is the cumulative prospect value of path k between O-D pair w; θ is a dispersion parameter, which characterizes the familiarity of a user with the road network; Km is set of all paths included in nest m; 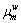 is nesting coefficients solved as
is nesting coefficients solved as 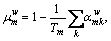 where Tm is the number of paths containing link m;
where Tm is the number of paths containing link m; 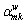 is inclusion coefficient, computed as
is inclusion coefficient, computed as 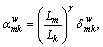 where Lm is the length of link m, Lk is the length of path k;
where Lm is the length of link m, Lk is the length of path k; 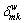 equals 1 if link m is on path k between O-D pair w and 0 otherwise, and γ is a parameter that characterizes the travelers’ perception of the similarities between different routes, assumed as γ=1.
equals 1 if link m is on path k between O-D pair w and 0 otherwise, and γ is a parameter that characterizes the travelers’ perception of the similarities between different routes, assumed as γ=1.
It is possible to decompose Eq. (14) as marginal probability and conditional probability, that is
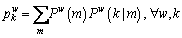 (15)
(15)
where Pw(m) is the marginal probability that the travelers choose nest m between O-D pair w, described as:
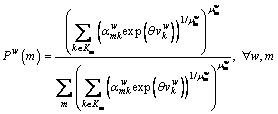 (16)
(16)
and 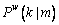 is the conditional probability, namely, the probability of choosing path k when the nest m is selected, described as
is the conditional probability, namely, the probability of choosing path k when the nest m is selected, described as
 (17)
(17)
3.3 CPV-based GNL SUE model
Based on the CPV-based route choice model, the CPV-based GNL SUE model is developed by incorporating the SUE condition. According to SHEFFI [2], SUE conditions of the CPV-based GNL SUE model can be described as:
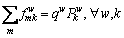 (18)
(18)
In addition, the regular network constraints must hold, that is:
 (19)
(19)
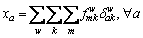 (20)
(20)
 (21)
(21)
where qw is the travel demand between O-D pair w; xa is the flow on link a and 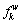 is the flow on path k between O-D pair w;
is the flow on path k between O-D pair w; 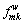 is the flow on path k of nest m between O-D pair w.
is the flow on path k of nest m between O-D pair w.
Equation (19) is the flow conservation constraints, Eq. (20) denotes the incidence relationship between link-path flow, specifically 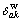 equals 1 if link a is a part of path k, and
equals 1 if link a is a part of path k, and 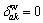 otherwise, Eq. (21) is the flow nonnegativity constraint.
otherwise, Eq. (21) is the flow nonnegativity constraint.
4 Mathematical formulation for CPV-based GNL SUE model
In this section, we develop the mathematical model and the associated MSA-based solution for the proposed CPV-based GNL SUE model. Furthermore, we prove the existence and equivalence between the proposed CPV-based GNL SUE model and the mathematical model.
4.1 Equivalent mathematical model
Given that the model proposed in this paper replaces the utility values with the cumulative prospect values, the route choice behavior described corresponds to actual road conditions. The objective function of the proposed model should include modified user equilibrium term using the cumulated prospect values instead of the utility values (i.e., Z1). According to the mathematical formulation for the traditional GNL-SUE problem proposed by BEKHOR et al [3], the objective function of the proposed model can also be decomposed into two entropy terms (i.e., Z2 and Z3). Therefore, the proposed CPV-based GNL SUE model is reformulated as the following equivalent mathematical model.
min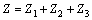 ,
,
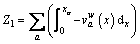 ,
,
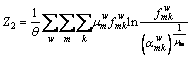 ,
,
 ,
,
s.t.
Eqs. (19)-(21) (22)
4.2 Existence and equivalency proof
Proposition 1: The mathematical model is equivalent to the CPV-based GNL SUE model.
Proof: The Lagrangian function of the mathematical model with respect to the equality constraints (19)-(21) can be formulated as:
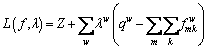 (23)
(23)
where λw represents the dual variable associated with the flow conservation constraint in Eq. (19).
Note that the first-order conditions of the proposed mathematical model and the first-order conditions of Lagrangian function are equal. For the first-order conditions of Lagrangian function, at the stationary point, the path flow variables must satisfy the following conditions:
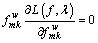 and
and 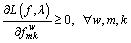 (24)
(24)
If 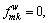 the Lagrangian function is meaningless, so
the Lagrangian function is meaningless, so 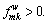 In this case, Eq. (24) can be written as:
In this case, Eq. (24) can be written as:
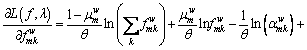
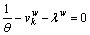 (25)
(25)
After a series of transformation, Eq. (25) can be written as:
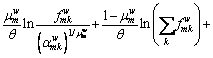
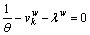 (26)
(26)
After multiplying both sides by θ, dividing both sides by 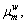 and taking the logarithm of exp as the base, Eq. (26) can be rewritten as:
and taking the logarithm of exp as the base, Eq. (26) can be rewritten as:
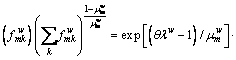
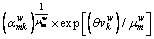 (27)
(27)
Summing Eq. (27) by route k, we have
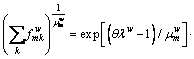
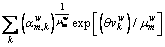 (28)
(28)
Elevating both sides to  , we have
, we have
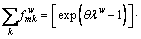
 (29)
(29)
Summing Eq. (29) by link (nest) m, we have
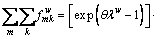
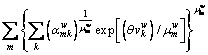 (30)
(30)
After Eq. (29) is divided by Eq. (30), the marginal probability is obtained as:
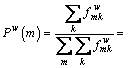
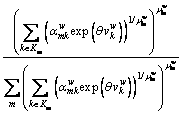 (31)
(31)
The conditional probability is obtained by dividing Eq. (28) by Eq. (29) as:
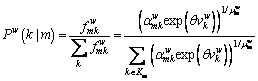 (32)
(32)
Equations (31) and (32) correspond to Eqs. (16) and (17). In this way, the mathematical formulation presented in Eq. (22) corresponds to the CPV-based GNL SUE formulation, for which the path-flow solution can be obtained according to the GNL model based on CPT.
Proposition 2: The proposed mathematical model has at least one solution.
Proof: Equation (25) can be transformed into the equivalent variational inequality as follows:
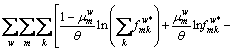
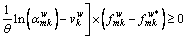 (33)
(33)
Let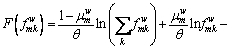
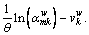 It is assumed that the distribution function of the link travel time is a continuous function of the link flow. Further, RP and CPV are also continuous functions of the path flow based on Eqs. (6)-(11). Therefore,
It is assumed that the distribution function of the link travel time is a continuous function of the link flow. Further, RP and CPV are also continuous functions of the path flow based on Eqs. (6)-(11). Therefore, 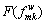 is a continuous function of the path flow. In addition, according to constraints (19)-(21), the feasible path flow set is a compact convex set. Based on the variational inequality theorem, the solution of Eq. (22) exists.
is a continuous function of the path flow. In addition, according to constraints (19)-(21), the feasible path flow set is a compact convex set. Based on the variational inequality theorem, the solution of Eq. (22) exists.
4.3 Solution algorithm
In general, the method of successive averages (MSA) proposed by POWELL et al [39] is simple and easier to practice in engineering. Therefore, in this paper, we modify the conventional MSA algorithm to solve the proposed mathematical model. The steps are presented below.
Step 1: Initialization
Determine the effective path set. According to Eq. (1), calculate the link travel time Ta based on initial free-flow travel time 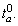 For each O-D pair, mean and variance of link travel time
For each O-D pair, mean and variance of link travel time 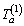 are calculated based on Eqs. (2) and (3), and then calculate the mean and variance of path travel time
are calculated based on Eqs. (2) and (3), and then calculate the mean and variance of path travel time 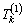 based on Eqs. (4) and (5). On this basis, calculate RP u(1) and the CPV v(1) of each path based on Eqs. (8) and (11). Use Eq. (18) to calculate path flow f (n), and then calculate link flow x(n) based on Eq. (20). Set iteration counter n=1.
based on Eqs. (4) and (5). On this basis, calculate RP u(1) and the CPV v(1) of each path based on Eqs. (8) and (11). Use Eq. (18) to calculate path flow f (n), and then calculate link flow x(n) based on Eq. (20). Set iteration counter n=1.
Step 2: Update
Calculate the new mean and variance of link travel time 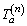 and path travel time
and path travel time 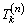 using Eqs. (2)-(5). For each O-D pair, re-determine the RP u(n) and recalculate the CPV v(n) of each path based on the updated mean and variance of each path travel time.
using Eqs. (2)-(5). For each O-D pair, re-determine the RP u(n) and recalculate the CPV v(n) of each path based on the updated mean and variance of each path travel time.
Step 3: Direction finding
According to Eq. (18), the auxiliary path flow g(n) is calculated.
Step 4: Move
Update the path flow based on the method of successive average. Set 
 Note that step size is the reciprocal of the number of iterations, i.e., 1/n.
Note that step size is the reciprocal of the number of iterations, i.e., 1/n.
Step 5: Convergence test
If 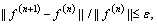 then stop. If not, set n=n+1 and go to Step 2.
then stop. If not, set n=n+1 and go to Step 2.
5 Numerical examples
The purpose of this section is to demonstrate the performance of the proposed CPV-based GNL SUE model. To this end, we first select a small network to test the performance of the proposed model in dealing with the overlapping path issue. Then, the Nguyen-Dupuis network is selected to demonstrate the ability of the proposed model in dealing with the perfectly rational issue. Finally, we select the Sioux Falls network to test the applicability of the proposed model for large road networks.
5.1 Small network: Solving overlapping path issue
5.1.1 Network introduction
The small network includes 1 O-D pair and 5 links, as shown in Figure 1. The O-D demand is 1000. The parameters in the BPR function are α=0.15 and β=4. The dispersion parameter θ in Eq. (16) is set as 0.5. The on-time arrival probability ρ in Eq. (6) is assumed to be 0.8. According to TVERSKY et al [32], the parameters of the value function in Eq. (9) are assumed to be  and μ=2.25. According to PRELEC [38], the probability weighting function in Eq. (10) is considered as γ=0.74. The iteration accuracy ε of the MSA algorithm is set as 0.0001. The free-flow travel time and capacity of each link are shown in Table 1, and the path composition and path length are exhibited in Table 2 (The values in Tables 1 and 2 are adopted from LI et al [30]).
and μ=2.25. According to PRELEC [38], the probability weighting function in Eq. (10) is considered as γ=0.74. The iteration accuracy ε of the MSA algorithm is set as 0.0001. The free-flow travel time and capacity of each link are shown in Table 1, and the path composition and path length are exhibited in Table 2 (The values in Tables 1 and 2 are adopted from LI et al [30]).
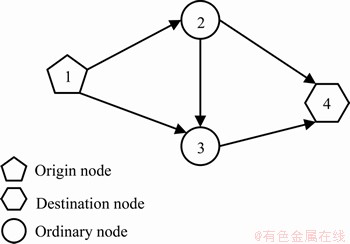
Figure 1 Small network with 1 O-D pair and 5 links
Table 1 Link characteristics
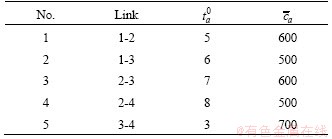
Table 2 Path composition and length

5.1.2 Link flow comparison
To demonstrate the capability of the proposed CPV-based GNL SUE model in dealing with the overlapping path problem, we run the CPV-based GNL SUE model and the CPV-based MNL SUE model on this small network. The CPU times required for the proposed CPV-based GNL SUE model and the CPV-based MNL SUE model to solve small network are 2.61 and 3.29 s, respectively. The link flow at equilibrium is shown in Figure 2.
In Figure 2, it can be seen that the link flows assigned by the CPV-based GNL SUE model on the overlapping links (e.g., link 1 and link 5) are smaller than those of the CPV-based MNL SUE model, while the link flows assigned by the CPV-based GNL SUE model on the non-overlapping links (e.g., link 2 and link 4) are larger than those of the CPV-based MNL SUE model. This is because the CPV-based GNL SUE model overcomes this deficiency by considering the similarity among various paths, so that the links with multiple overlapping paths are assigned less flows than the CPV-based MNL SUE model. In contrast, the CPV-based MNL SUE model does not consider the similarities between these different paths, so that the flows of the overlapping links are overestimated.
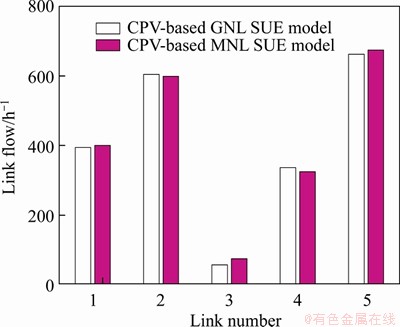
Figure 2 Link flows assigned by CPV-based GNL SUE model and CPV-based MNL SUE model
5.1.3 Impact analysis of model parameters
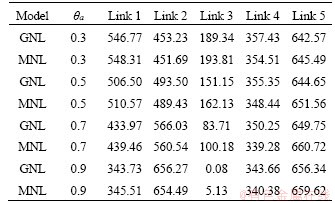
In order to show the stability of the proposed CPV-based GNL SUE model, we vary the dispersion parameter θ and the worst-degraded coefficient θa to analyse how the changes in these parameters will affect the path flows at equilibrium. For simplify, in Tables 3 and 4, we use different parts of the CPV-based GNL SUE model and the CPV-based MNL SUE model to distinguish them. It can be seen that for different θ and θa, the pattern of the link flows is the same, that is, the flows assigned by the CPV-based GNL SUE model on overlapping links (e.g., link 1 and link 5) are smaller than those of the CPV-based MNL SUE model, while the flows assigned by the CPV-based GNL SUE model on non-overlapping links (e.g., link 2 and link 4) are larger than those of the CPV-based MNL SUE model. Thus, it can be safely concluded that these model parameters do not change the relative performance of the CPV-based GNL SUE model and the CPV-based MNL SUE model.
Table 3 Variations of link flows for different values of θ
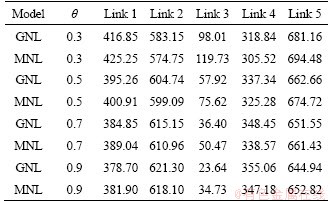
Table 4 Variations of link flows for different values of θa
5.2 Nguyen-Dupuis network: Solving perfectly rational issue
5.2.1 Network introduction
The Nguyen-Dupuis network consists of 4 O-D pairs, 13 nodes, and 19 links, as shown in Figure 3. For each O-D pair, the travel demand is q1-2=660, q1-3=495, q4-2=412.5 and q4-3=495, respectively. The other parameters are the same as those in the small network.
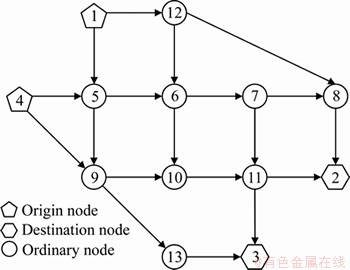
Figure 3 Nguyen and Dupuis network
The free-flow travel time, capacity, and the worst-degraded coefficient for each link on the network are shown in Table 5 (The values in Table 5 are adopted from XU et al [9]). The path composition and path length are exhibited in Table 6 (The values in Table 6 are adopted from JIANG et al [40]).
Table 5 Link characteristics

Table 6 Path composition and length

5.2.2 Path flow comparison
To demonstrate the capability of the proposed CPV-based GNL SUE model in dealing with the perfectly rational problem, we compare path flows assigned by the CPV-based GNL SUE model and the UV-based GNL SUE model running on the Nguyen-Dupuis network. The CPU times required for the proposed CPV-based GNL SUE model and the UV-based GNL SUE model to solve the Nguyen-Dupuis network are 188.81 and 3.68 s, respectively. It should be noted that CPU time required for the proposed CPV-based GNL SUE model may be longer than the UV-based GNL SUE model due to the complexity of the model. The path flow at equilibrium is shown in Tables 7 and 8.
In Tables 7 and 8, it can be seen first that the path flows assigned by the UV-based GNL SUE model and the CPV-based GNL SUE model are significantly different. This is because these two models have different behavioral assumptions. The UV-based GNL SUE model assumes that all travelers are perfectly rational when choosing a path. Consequently, they will definitely choose the path with the shortest travel time. In contrast, the CPV-based GNL SUE model assumes that the travelers are bounded rational when choosing a path. In other words, when travelers choose a path, they will first judge the gains and losses based on the reference point, and then, the travelers will combine the gains and losses with subjective probability weights to obtain the CPVs of different paths. In this way, the travelers will choose the path with the largest CPV. Second, it can be clearly seen that the CPV-based GNL SUE model assigns OD demand to each path based on the following criteria, that is, path with larger CPV is assigned more traffic flow, and vice versa. The UV-based GNL SUE model assigns OD demand to each path based on the following criteria: the smaller the mean travel time of the path, the less traffic flow is assigned to this path, and vice versa.
Table 7 Network equilibrium solution calculated by CPV-based GNL SUE model
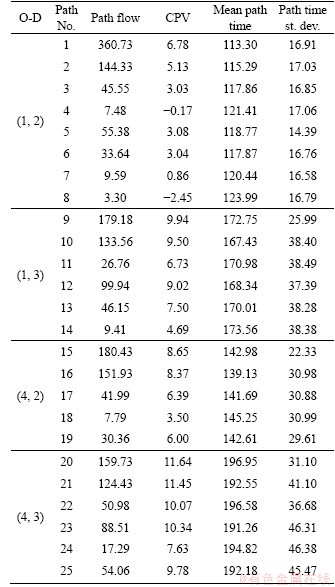
Table 8 Network equilibrium solution calculated by UV-based GNL SUE model
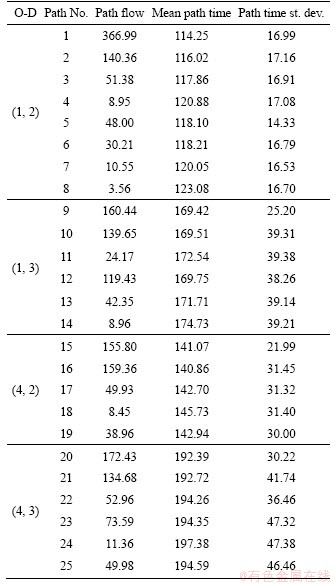
Finally, the results of the path flow assigned by the CPV-based GNL SUE model indicate that travelers consider both the mean path time and the standard deviation of the path time when choosing a route. However, the results of the path flow assigned by the UV-based GNL SUE model illustrate that travelers only consider mean path time when choosing a route. For example, in Table 7, some travelers choose paths with a high mean but low standard deviation (e.g., path 15 and path 20). In Table 8, all travelers tend to choose a path with a low mean without taking standard deviation into account at all.
In order to further demonstrate that the proposed CPV-based GNL SUE model has the capability to deal with perfectly rational issue, we compared the path flow assigned by the proposed CPV-based GNL SUE model under different on-time arrival probability ρ and the path flow assigned by the UV-based GNL SUE model. The results of path flow at equilibrium are shown in Table 9.
Table 9 Path flow assigned by CPV-based GNL SUE model under different ρ and UV-based GNL SUE model
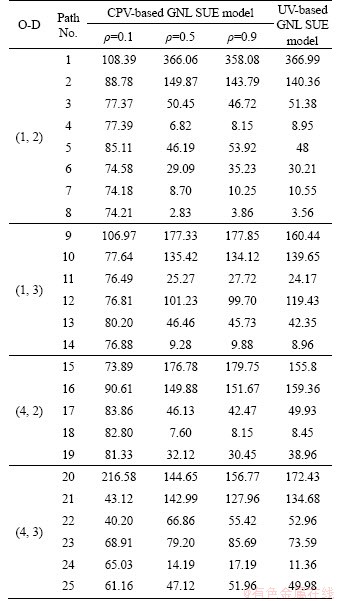
In Table 9, it can be seen that the proposed CPV-based GNL SUE model assigns different flows on each path under different on-time arrival probability ρ. When ρ=0.1, path flow tends to be evenly distributed. This is because the travelers believe that they may have chance of early arrival due to the variations of travel time. They then are willing to take a higher risk to minimize their travel time. These travelers are considered as the risk-prone travelers, so they choose the path randomly. When ρ gradually becomes larger, the travelers choose the paths with less travel time fluctuations, such as path 1 and path 2. This is due to the fact that the travelers are very keen on punctual arrivals because the penalty imposed to an unexpected late arrival is much higher than the bonus earned from an early arrival. In this case, these travelers are usually risk-averse when making route choice decisions. In contrast, no matter how ρ changes, the path flow assigned by the UV-based GNL SUE model is always the same. This is because travelers only care about the absolute value of path travel time, so when the on-time arrival probability ρ changes, their route choice decisions remain. Furthermore, the path flow also remains unchanged.
In addition, we randomly select O-D (1, 2) to analyze the impact of the on-time arrival probability ρ on RP and CPVs, as shown in Figure 4.
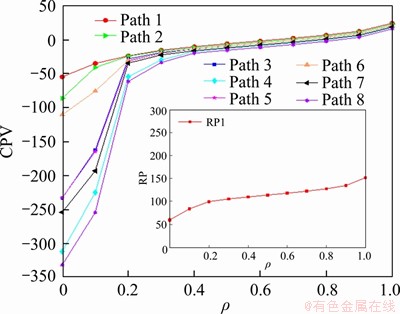
Figure 4 Variation of RP and CPVs with ρ
In Figure 4, it can be seen that the reference point gradually increases with the increase of on-time arrival probability ρ. In addition, it can also be seen from Figure 4 and Table 6 that as the reference point changes, CPVs and path flows at equilibrium also change accordingly. This means that the proposed CPV-based GNL SUE model has a significant reference-dependence effect. In other words, travelers make route choice decisions based on the reference point rather than the absolute value of the path travel time.
In summary, the path flow assigned by the UV-based GNL SUE model is based on the absolute value of path travel time, while the path flow assigned by the CPV-based GNL SUE model is based on the relative value, that is, the value of the path travel time relative to the reference point. In this way, it can be concluded that the proposed CPV-based GNL SUE model can deal with the perfectly rational issue.
5.2.3 Impact analysis of model parameters
In this section, we vary seven parameters, i.e., dispersion parameter θ, on-time arrival probability ρ, worst-degraded coefficient θa, loss-aversion coefficient μ, gain sensitivity coefficient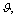 loss sensitivity coefficient η, and perceived probability coefficient γ, to analyze the variations in path flows at equilibrium assigned by the proposed CPV-based GNL SUE model. The results are shown in Figure 5.
loss sensitivity coefficient η, and perceived probability coefficient γ, to analyze the variations in path flows at equilibrium assigned by the proposed CPV-based GNL SUE model. The results are shown in Figure 5.
In addition, we provide the range for these seven parameters in Table 10. It is worth noting that since the parameters 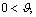 η, γ<1, we set the minimum and maximum ranges of these parameters to be 0.0001 and 0.9999, respectively. Meanwhile, since parameter θ belongs to [0, +∞) and parameter μ belongs to [1, +∞), we choose large enough steady state values through tests.
η, γ<1, we set the minimum and maximum ranges of these parameters to be 0.0001 and 0.9999, respectively. Meanwhile, since parameter θ belongs to [0, +∞) and parameter μ belongs to [1, +∞), we choose large enough steady state values through tests.
On observing Figure 5, first, it can be seen from Figure 5(a) that when θ falls in [0, 4], the variation of path flow is relatively large, when θ falls in (4, 18), there is a relatively slight change in path flow, and when θ falls in [18, +∞), there is no change in flow on the path. This is because that a smaller θ indicates that the travelers are not familiar with the road network conditions, so that they tend to randomly choose a path. In contrast, a larger θ indicates that the travelers are more familiar with the road network conditions, and the route choice behavior of the travelers will be close to deterministic choice.
Second, it can be observed from Figures 5(b)- (d) in Figure 5 that for the worst-degraded coefficient θa, most of the steady changes in path flow are concentrated in (0.3, 0.9). This is because that a larger θa indicates more reliable path travel time. For the on-time arrival probability ρ, when ρ falls in [0, 0.4], the variation of the path flow is relatively large, and when ρ falls in (0.4, 1], the variation of the path flow is not significant. This is because that a higher ρ implies that the travelers are very keen on punctual arrivals, such that the travelers are generally classified as risk-averse travelers. For the parameter γ, when it increases, the path flows will gradually tend to steady state. This is because that the larger the γ, the closer the perceived probability of the travelers are to the actual probability. Note that these changes only apply to the proposed CPV-based GNL SUE model.
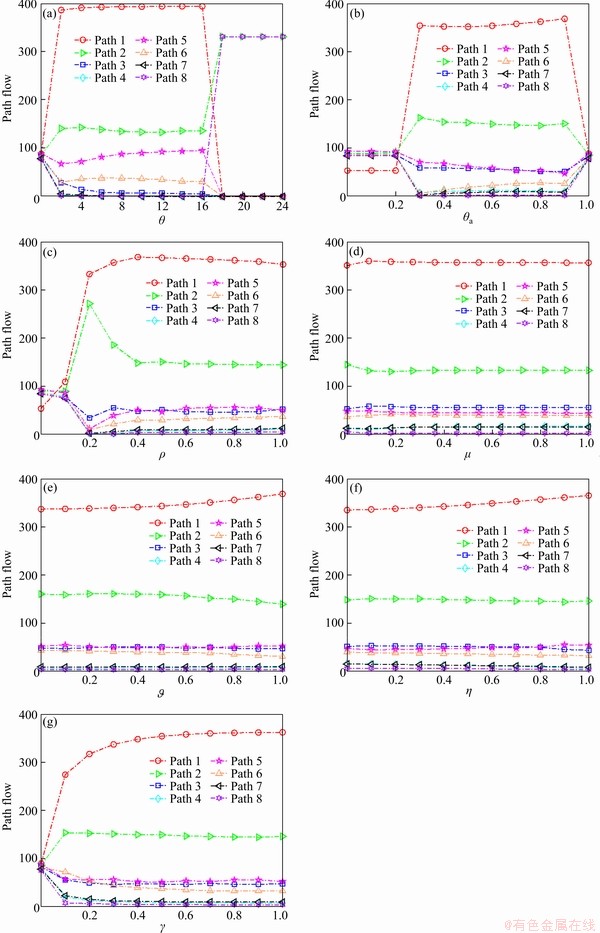
Figure 5 Path flow variations with respect to different parameter values
Table 10 Range of parameter
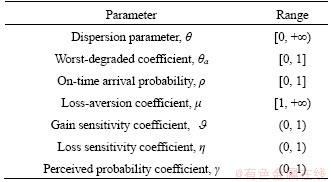
Finally, it can be seen from Figures 5(d)-(f) that the other three parameters, i.e., the loss-aversion coefficient μ, the gain sensitivity coefficient 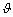 , and the loss sensitivity coefficient η, have little effect on the path flows.
, and the loss sensitivity coefficient η, have little effect on the path flows.
In summary, travellers usually choose the path based on the CPV of this path. Moreover, the dispersion parameters θ, the on-time arrival probability ρ, the worst-degraded coefficient θa, and the perceived probability coefficient γ have significant influences on the path flows at equilibrium, while the influence of other parameters on the path flows is not significant. In addition, the range of steady-state path flows corresponding to each parameter is obtained. Further, this provides a reference for how to choose an appropriate parameter value.
5.3 Sioux Falls network: Solving practical applications
5.3.1 Network introduction
The Sioux Falls network consists of 24 nodes, 76 links, 528 O-D pairs, and 1342 paths as shown in Figure 6. Compared to the previous two networks, this network can be considered as a larger network, which can be regarded as comparable to the real world transportation networks.
The free-flow travel time on link a, i.e., 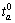 and design capacity of link a, i.e.,
and design capacity of link a, i.e.,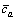 are shown in Table 11 (The values in Table 11 are adopted from LEBLANC [41] and WANG et al [42], respectively). The worst-degraded coefficient for each link is set to 0.8. The iteration accuracy ε of the MSA algorithm is set as 0.01. The values of the other parameters are the same as those of the small network.
are shown in Table 11 (The values in Table 11 are adopted from LEBLANC [41] and WANG et al [42], respectively). The worst-degraded coefficient for each link is set to 0.8. The iteration accuracy ε of the MSA algorithm is set as 0.01. The values of the other parameters are the same as those of the small network.
5.3.2 Convergence of propose model
To demonstrate the applicability of the proposed CPV-based GNL SUE model on a larger network, we run the proposed model and the associated MSA algorithm on this Sioux Falls network. The numbers of iterations and the CPU time required for the CPV-based GNL SUE model to solve Sioux Falls network are 56.00 and 160.50 s, respectively. The convergence process of the CPV-based GNL SUE model solved in the Sioux Falls network is depicted in Figure 7.

Figure 6 Sioux Falls network
It can be seen from Figure 7 that the convergence speed of the improved MSA algorithm is fast and the convergence value is approaching to 0 before the number of iterations is approaching to 10. In contrast, after the number of iterations is larger than 10, the convergence value gradually tends to a steady state of zero. Based on the above pattern, the proposed model can be solved in this larger network efficiently. Note that this entire convergence pattern is also consistent with that of the traditional MSA algorithm. Thus, it is safe to conclude that the proposed model is applicable for large road networks with more than 20 nodes and more than 500 O-D pairs.
6 Conclusions
Traffic assignment is vital for policy makings in transportation management and operations, and many studies have been devoted in this field. However, the joint solution to the path overlapping issue and the perfectly rational issue are still lack of adequate investigations in the context of traffic assignment. Therefore, in this paper, a CPV-based GNL SUE model is proposed through using CPV instead of the utility value as the path performance in the GNL model framework. For this proposed model, an equivalent mathematical model is provided together with the associated MSA based solution. The existence and equivalence of solution are also proved.
Table 11 Link capacity and free-flow travel time
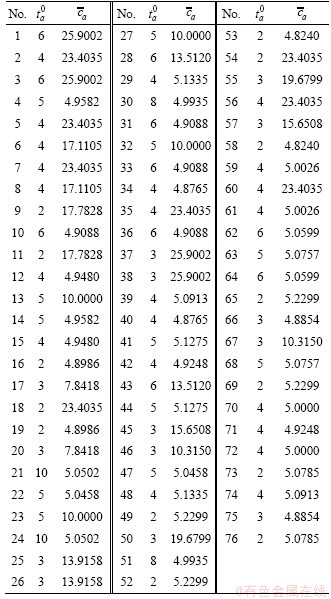
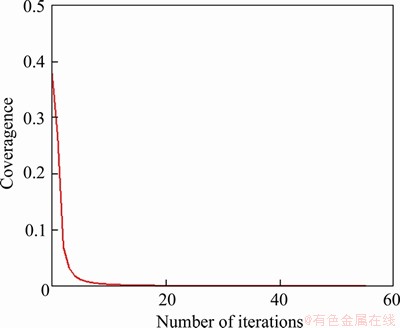
Figure 7 Convergence process of improved MSA algorithm
The proposed CPV-based GNL SUE model is tested in three networks to demonstrate its performance. The results show that the proposed model can handle jointly the overlapping path issue and the perfectly rational issue. In addition, the proposed model is also shown to be applicable to real world large networks. The impact of the parameters is also investigated to show their impacts on the performances of the proposed model.
For this proposed model, we only consider single-class user. Therefore, multiclass users will be considered in the modeling process in the future. In addition, doubly uncertain road network with stochastic demand and stochastic link capacity degradation will also be considered in future research to meet the real world requirements.
Contributors
YAN Dong-mei edited the draft of manuscript. GUO Jian-hua provided the concept and design. Both authors reviewed the results and approved the final version of the manuscript.
Conflict of interest
YAN Dong-mei and GUO Jian-hua declare that they have no conflict of interest.
References
[1] DAGANZO C F, SHEFFI Y. On stochastic models of traffic assignment [J]. Transportation Science, 1977, 11: 253-274. DOI: 10.1287/trsc.11.3.253.
[2] SHEFFI Y. Urban transportation networks [M]. New Jersey: Prentice-Hall, 1985.
[3] BEKHOR S, PRASHKER J N. Stochastic user equilibrium formulation for generalized nested logit model [J]. Transportation Research Record Journal of the Transportation Research Board, 2001, 1752: 84-90. DOI: 10.3141/1752-12.
[4] BEKHOR S, REZNIKOVA L, TOLEDO T. Application of cross-nested logit route choice model in stochastic user equilibrium traffic assignment [J]. Transportation Research Record: Journal of the Transportation Research Board, 2007, 2003: 41-49. DOI: 10.3141/2003-06.
[5] BEKHOR S, TOLEDO T, REZNIKOVA L. A path-based algorithm for the cross-nested logit stochastic user equilibrium traffic assignment [J]. Computer-Aided Civil and Infrastructure Engineering, 2010, 24(1): 15-25. DOI: 10.1111/j.1467-8667.2008.00563.x.
[6] CHEN A, PRAVINVONGVUTH S, XU Xiang-dong, RYU S, CHOOTINAN P. Examining the scaling effect and overlapping problem in logit-based stochastic user equilibrium models [J]. Transportation Research Part A: Policy and Practice, 2012, 46: 1343-1358. DOI: 10.1016/ j.tra.2012.04.003.
[7] AVINERI E, PRASHKER J N. Violations of expected utility theory in route-choice stated preferences [J]. Transportation Research Record: Journal of the Transportation Research Board, 2004, 1894: 222-229. DOI: 10.3141/1894-23.
[8] WANG Qian, XU Wei. A user equilibrium model based on cumulative prospect theory for degradable transport network [C]// 4th International Joint Conference on Computational Sciences and Optimization (CSO). IEEE. 2011: 1078-1082. DOI: 10.1109/CSO.2011.62.
[9] XU Hong-li, LOU Ying-yan, YIN Ya-feng, ZHOU Jing. A prospect-based user equilibrium model with endogenous reference points and its application in congestion pricing [J]. Transportation Research Part B: Methodological, 2011, 45(2): 311-328. DOI: 10.1016/j.trb.2010.09.003.
[10] JOU Rong-chang, CHEN Ke-hong. An application of cumulative prospect theory to freeway drivers’ route choice behaviours [J]. Transportation Research Part A: Policy and Practice, 2013, 49: 123-131. DOI: 10.1016/j.tra.2013.01.011.
[11] YANG Ju-fen, JIANG Gui-yan. Development of an enhanced route choice based on cumulative prospect theory [J]. Transportation Research Part C: Emerging Technologies, 2014, 47: 168-178. DOI: 10.1016/j.trc.2014.06.009.
[12] HOROWITZ J. Reconsidering the multinomial probit model [J]. Transportation Research Part B: Methodological, 1991, 25(6): 433-438. DOI: 10.1016/0191-2615(91)90036-I.
[13] MCFADDEN D. A method of simulated moments for estimation of discrete response models without numerical integration [J]. Econometrica, 1989, 57(5): 995-1026. DOI: https://doi.org/0012-9682(198909)57:5<995:AMOSMF>2.0. CO;2-Z.
[14] PRASHKER J N, BEKHOR S. Route choice models used in the stochastic user equilibrium problem: A review [J]. Transport Reviews, 2004, 24(4): 437-463. DOI: 10.1080/0144164042000181707.
[15] FREJINGER E, BIERLAIRE M. Capturing correlation with subnetworks in route choice models [J]. Transportation Research Part B: Methodological, 2007, 41(3): 363-378. DOI: 10.1016/j.trb.2006.06.003.
[16] LAI Xin-jun, LI Jun. Modelling stochastic route choice behaviours with a closed-form mixed logit model [J]. Mathematical Problems in Engineering, 2015, 1-9. DOI: 10.1155/2015/729089.
[17] ZHOU Zhong, CHEN A, BEKHOR S. C-logit stochastic user equilibrium model: Formulations and solution algorithm [J]. Transportmetrica, 2012, 8(1): 17-41. DOI: 10.1080/ 18128600903489629.
[18] LIU B Q, ZHANG Y H, DU W. A simplified C-logit stochastic user equilibrium model on bimodal transportation network [J]. Mathematical Problems in Engineering, 2020, 2020: 1-8. DOI: 10.1155/2020/3702965.
[19] YONG Gui, HUANG Hai-jun, LIU Tian-liang, XU Yan. Bounding the inefficiency of the C-Logit stochastic user equilibrium assignment [J]. Journal of Systems Science and Complexity, 2016, 29(6): 1629-1649. DOI: 10.1007/s11424-016-4320-4.
[20] DUNCAN L C, WATLING D P, CONNORS R D, RASMUSSEN T K, NIELSEN O A. Path size logit route choice models: Issues with current models, a new internally consistent approach, and parameter estimation on a large-scale network with GPS data [J]. Transportation Research Part B: Methodological, 2020, 135: 1-40. DOI: 10.1016/j.trb. 2020.02.006.
[21] QIU Song-Lin, CHENG Lin, XU Xiang-dong. Path-size logit-based stochastic user equilibrium assignment model [J]. Journal of Southeast University(Science and Technology), 2012, 42(1): 173-176. DOI: 10.3969/j.issn.1001-0505. 2012.01.032. (in Chinese)
[22] PRASHKER J N, BEKHOR S. Investigation of stochastic network loading procedures [J]. Transportation Research Record Journal of the Transportation Research Board, 1998, 1645: 94-102. DOI: 10.3141/1645-12.
[23] PAPOLA A, MARZANO V. A network generalized extreme value model for route choice allowing implicit route enumeration [J]. Computer-Aided Civil and Infrastructure Engineering, 2013, 28(8): 560-580. DOI: 10.1111/ mice.12007.
[24] MCFADDEN D. Modelling the choice of residential location [J]. Transportation Research Record Journal of the Transportation Research Board, 1978, 673(672): 72-77.
[25] LU Xiao-shan, LIU Tian-liang, HUANG Hai-jun. Pricing and mode choice based on nested logit model with trip-chain costs [J]. Transport Policy, 2015, 44: 76-88. DOI: 10.1016/ j.tranpol.2015.06.014.
[26] KAROONSOONTAWONG A, LIN Dung-ying. Combined gravity model trip distribution and paired combinatorial logit stochastic user equilibrium problem [J]. Networks and Spatial Economics, 2015, 15(4): 1011-1048. DOI: 10.1007/s11067-014-9279-x.
[27] RYU S, CHEN A, XU Xiang-dong, CHOI K. Modeling demand elasticity and route overlapping in stochastic user equilibrium through paired combinatorial logit model [J]. Transportation Research Record: Journal of the Transportation Research Board, 2014, 2429: 8-19. DOI: 10.3141/2429-02.
[28] WANG Jian, PEETA S, HE Xiao-zheng, ZHAO Jin-bao. Combined multinomial logit modal split and paired combinatorial logit traffic assignment model [J]. Transportmetrica A: Transport Science, 2018, 14(9): 737-760. DOI: 10.1080/23249935.2018.1431701.
[29] ZHANG R, YAO E J, PAN L. Optimizing EV-based P&R subsidy policies for commuting corridor based on cross-nested logit model [J]. International Journal of Sustainable Transportation, 2019, 13(7): 461-478. DOI: 10.1080/ 15568318.2018.1482032.
[30] LI Xue-fei, LANG Mao-xiang. Multi-class and multi-criteria stochastic user equilibrium model based on generalized nested logit model [J]. Journal of Transportation Systems Engineering and Information Technology, 2014, 14(4): 139-145. DOI: 10.16097/j.cnki.1009-6744.2014.04.024.
[31] KAHNEMAN D, TVERSKY A. A prospect theory: An analysis of decisions under risk [J]. Econometrics, 1979, 47: 313-327. DOI: 10.2307/1914185.
[32] TVERSKY A, KAHNEMAN D. Advances in prospect theory: Cumulative representation of uncertainty [J]. Journal of Risk and Uncertainty, 1992, 5(4): 297-323. DOI: 0.1007/978-3-319-20451-2_24.
[33] CONNORS R D, SUMALEE A. A Network equilibrium model with travelers’ perception of stochastic travel times [J]. Transportation Research Part B: Methodological, 2009, 43(6): 614-624. DOI: 10.1016/j.trb.2008.12.002.
[34] WANG Wei, SUN Hui-jun. Cumulative prospect theory-based user equilibrium model with stochastic perception errors [J]. Journal of Central South University, 2016, 23(9): 2465-2474. DOI: 10.1007/s11771-016-3305-8.
[35] Bureau of Public Roads. Traffic assignment manual [M]. Washington DC: US Department of Commerce, Urban Planning Division, 1964.
[36] LO H K, LUO X W, SIU B W Y. Degradable transport network: Travel time budget of travelers with heterogeneous risk aversion [J]. Transportation Research Part B: Methodological, 2006, 40(9): 792-806. DOI: 10.1016/ j.trb.2005.10.003.
[37] SHASHKIN A. A functional central limit theorem for the level measure of a Gaussian random field [J]. Statistics & Probability Letters, 2013, 83(2): 637-643. DOI: 10.1016/ j.spl.2012.11.007.
[38] PRELEC D. The probability weighting function [J]. Econometrica, 1998, 66(3): 497-527. DOI: 10.2307/2998573.
[39] POWELL W B, SHEFFI Y. The convergence of equilibrium algorithms with predetermined step sizes [J]. Transportation Science, 1982, 16(1): 45-55. DOI: 10.1287/trsc.16.1.45.
[40] JIANG Nan, XIE Chi. Computing and analyzing mixed equilibrium network flows with gasoline and electric vehicles [J]. Computer-Aided Civil and Infrastructure Engineering, 2014, 29(8): 626-641. DOI: 10.1111/mice.12082.
[41] LEBLANC L J. An algorithm for the discrete network design problem [J]. Transportation Science, 1975, 9(3): 183-199. DOI: 10.1287/trsc.9.3.183.
[42] WANG Tong-gen, XIE Chi, XIE Jun, WALLER T. Path-constrained traffic assignment: A trip chain analysis under range anxiety [J]. Transportation Research Part C: Emerging Technologies, 2016, 68: 447-461. DOI: 10.1016/j.trc.2016. 05.003.
(Edited by FANG Jing-hua)
中文导读
一种解决路径重叠和完全理性问题的随机用户平衡模型
摘要:交通分配是交通规划和运营的关键技术之一。为了更好地解决交通分配过程中涉及的期望效用理论(EUT)的完全理性问题和多项式logit(MNL)模型的路径重叠问题,本文提出了基于累积前景值(CPV)的广义巢式logit(GNL)随机用户平衡(SUE)模型,即基于CPV的GNL SUE模型。该模型在GNL模型框架内使用CPV代替效用值作为路径性能。对于该模型,给出等价的数学模型,并使用相继平均法(MSA)对该数学模型进行求解,同时模型解的存在性和等价性也被证明。为了展示基于CPV的GNL SUE模型的性能,选择三个道路网络作为测试实例,结果表明,提出的模型可以同时处理完全理性问题和路径重叠问题,并且适用于大型道路网络。
关键词:随机用户均衡;累积前景理论;广义巢式logit;相继平均法
Foundation item: Project(KYLX16_0271) supported by the Postgraduate Research & Practice Innovation Program of Jiangsu Province, China
Received date: 2020-04-28; Accepted date: 2020-08-31
Corresponding author: GUO Jian-hua, PhD, Professor; Tel: +86-13701586076; E-mail: seugjh@163.com; ORCID: https://orcid.org/0000-0002-7239-653X
Abstract: Traffic assignment has been recognized as one of the key technologies in supporting transportation planning and operations. To better address the perfectly rational issue of the expected utility theory (EUT) and the overlapping path issue of the multinomial logit (MNL) model that are involved in the traffic assignment process, this paper proposes a cumulative prospect value (CPV)-based generalized nested logit (GNL) stochastic user equilibrium (SUE) model. The proposed model uses CPV to replace the utility value as the path performance within the GNL model framework. An equivalent mathematical model is provided for the proposed CPV-based GNL SUE model, which is solved by the method of successive averages (MSA). The existence and equivalence of the solution are also proved for the equivalent model. To demonstrate the performance of the proposed CPV-based GNL SUE model, three road networks are selected in the empirical test. The results show that the proposed model can jointly deal with the perfectly rational issue and the overlapping path issue, and additionally, the proposed model is shown to be applicable for large road networks.


