J. Cent. South Univ. Technol. (2007)04-0552-05

DOI: 10.1007/s11771-007-0106-0

Dynamics of vertical pipe in deep-ocean mining system

YU Hong-yun(禹宏云), LIU Shao-jun(刘少军)

(School of Mechanical and Electrical Engineering, Central South University, Changsha 410083, China)

__________________________________________________________________________________________________

Keywords: deep-ocean mining; dynamics; vertical pipe; finite element method; geometrical nonlinearity

__________________________________________________________________________________________________

1 Introduction

With 20 some years’ research experience, self-propel miner incorporating with lift unit of mine-slurry bump is regarded as a promising deep-ocean mining system. This system consists of miner, flexible riser, buffer, vertical pipe (including pump) and ship^[1-2]. The analysis of the configuration and intensity of the vertical pipe is significant to design, control and safety of practical mining system. Being affected by gravity, buoyancy, and interaction with wave and current, the lift unit is a complicated dynamic system, and requires much consideration of various factors. There have been some research works done on the dynamics of the vertical pipe (including the pump and buffer)^[3-7], but in most of these researches, the bottom of the buffer was simply treated as one free end^[7-10]. In reality, the top of the vertical pipe is connected to the ship, the bottom of the vertical pipe is connected to the miner via the buffer and flexible riser^[11-15]. As a result, the combining motion of ship and miner leads to interaction between the buffer and flexible riser and affects the force and configuration of the vertical pipe. By ignoring the interaction force and restriction at the bottom of the vertical pipe, those analytical results might bring much difference from reality. After comparison of several methods, this research employs finite element method (FEM) to analyse the dynamics of the vertical pipe of 1000-m sea trial system of China Ocean Mineral Resources R&D Association (COMRA) by taking the entire lift system together (including vertical pipe, pump, buffer and flexible riser) into consideration.

In deep-ocean, the lift system shows 3-D geometric nonlinearity characteristics of large deflection and small strain, and it may suffer axial tension-compression, bending and torsion deformations. The lift system is discretized into 3-D pipe element, each element includes two nodes, and each node includes 6 degrees of freedom (translations in the x, y and z directions and rotations about x, y and z-axes).

2.1 Dynamics equation

As to geometric nonlinearities of the structural model, the equation of motion in increment type is represented by

 (1)

where  [M] is the consistent mass matrix, and is independent of time; [C(t)] is the structural damping matrix at time t, and Rayleigh damping (α and β damping) is used to calculate the damping matrix [C(t)]=[αM]+β[K(t)]; K(t) is the whole stiffness matrix at time t, which includes linear axial, bending, torsional stiffness matrix and nonlinear initial displacement, initial stress stiffness matrix; [ΔU(t)] is the increment of displacement of node from time t to time t+Δt; [ΔF(t)] is the increment of external force of node from time t to time t+Δt.

As to the external forces on the lift system, we considered the following factors: gravity force, buoyancy force, internal and external fluid pressures, friction force of internal slurry flow, hydrodynamic force exerted by current, wave and pipe motion, along with other force (such as pumping force, hanging force on the flexible riser). The hydrodynamic force related to fluid-pipe coupling was calculated with Morison equation, whereas the pipe was regarded as slender, and stable current, regular wave and pipe motion were considered^[13-16].

2.2 Correlative condition and model of system

Referring to the whole project of COMRA’s 1 000 m sea trial system, the following joint patterns were used in this research:

1) The two ends of the buffer are sphere hinged to the vertical pipe and flexible riser respectively.

2) The two ends of the lift system are cross hinged to the ship and miner respectively, with no rotation about the pipe axis.

At the top and bottom of the lift system, the movable boundary conditions depend on the position-time function of the ship and miner respectively.

The depth of seawater is 1 000 m. According to related data, it is supposed that the steady current velocity varies exponentially with the depth, which is 0.772 m/s on the surface of the ocean and becomes 0.100 m/s at the seafloor. The effect of wave is simulated as harmonious heave movement, and wave period is assumed to be 8 s according to the operational condition.

In this research, ANSYS (a commercial FEM software) was utilized in modeling and programming. The vertical pipe, pump, buffer and flexible riser in the lift system were all modeled with pipe element in ANSYS. Relative to the flexible riser, the vertical pipe has less deformation, and can be divided into more sparse elements than the flexible riser. By preparatory calculation, some regions of more deformation in the vertical pipe, such as elements near the ocean surface and the bump, can be found, correspondingly, these elements should be shorter to ensure the analysis precision. In this lift system, the length of the vertical pipe and flexible riser are 900 and 400 m, respectively, and the element division is shown in Fig.1.

Fig.1 Element division of lift system

The steady current is assumed opposite to x direction. Both the ship and miner move along x direction (against the current) at velocity of 0.50 m/s.

The coordinate is shown in Fig.2. Considering the depth and the relative position of the ship and miner at operation, it is assumed that the ship is at  (0, 0, 0), and correspondingly, the original static configuration is shown in Fig.2(a). The excursion of the buffer relative to the ship along the x-direction is 14 m. In the static state, for the vertical pipe, the maximum of the x-directional force, z-directional force and axial stress are all located at the top of the vertical pipe. The axial stress is dominant on the vertical pipe, which is 130.7 MPa and mainly caused by gravity. Element 57 (next to the pump) has the maximal bending stress of 2.9 MPa, which mainly results from the change of the diameter of the vertical pipe relative to that of the pump (element 56), and the obvious change of the current velocity here. The torsional stress is very small. All of these stresses are much less than the allowable stress of the vertical pipe and joint (about 860 MPa). the miner is at  (-240, 0, -1000), in the original state.

Fig.2 Configuration of lift system at different velocities against current

(a) Static state; (b) Steady state of 0.50 m/s; (c) Steady state of 1.00 m/s

As far as the ship and miner move simultaneously, our simulation results show that the higher the velocity, the more excursion the buffer. This is attributed to the relative velocity of water particle to the pipe. The quicker the movement of pipe, the faster the movement of water particle, and the larger the hydrodynamic force.

Figs.2(b) and (c) show the pipeline configuration in steady state at velocity of 0.50 and 1.00 m/s, respectively. At 0.5 m/s, the configuration of the flexible riser is good, and its horizontal resistance to the miner is only 4 611 N, which is in the operation range of the miner (less than  8 kN). The configuration of the flexible riser gets bad at 1.00 m/s, and its horizontal resistance to the miner reaches 18 079 N, which exceeds the operation range. However, at velocity above 0.50 m/s, the movement of the miner will be unfavorable. So, when the ship and miner move against the current, it is suggested that  0.50 m/s should be the moving velocity.

The following results are some simulation ones at the moving velocity of 0.50 m/s against the current.

3.1 Displacement of butter without heave movement caused by wave at pipe top

Fig.3 shows the historical curve of the x-directional displacement of the buffer. The buffer begins to move about 14 s later, and reaches the same velocity as the ship at time longer than 300 s. The buffer’s x-directional is about 50 m in steady moving state. Fig.4 shows the z-directional displacement of the buffer.

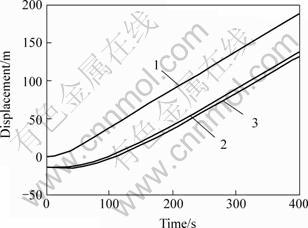
Fig.3 x-directional displacements of butter

1—Ship; 2—Buffer without heave; 3—Buffer with heave

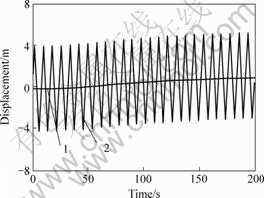
Fig.4 z-directional displacements of buffer

1—Without heave; 2—With heave

During moving, for the vertical pipe, the z-directional force, axial and torsional stresses are almost unchanged. Fig.5 shows the z-directional force at the pipe top. The force and x-directional bending stress increase significantly, for the higher the relative velocity of water particle against to the pipe, the larger x-directional hydrodynamic force. The maximal x-directional force is maintained at the pipe top, as shown in Fig.6, while element 57 still has the maximal bending stress (Figs.7 and 8).

Fig.5 z-directional forces at pipe top

1—Without heave; 2—With heave

Fig.6 x-directional forces at pipe top

1—Without heave; 2—With heave

Fig.7 Bending stress at element 57

1—Without heave; 2—With heave

Fig.8 Bending stress distribution in steady state

1—Against current; 2—Along current

3.2 Displacement of buffer with heave movement caused by wave at pipe top

The wave period is 8 s and the amplitude is 4 m.

As shown in Fig.3, the buffer begins to go forward about 35 s later after a brief backward. During moving, the buffer’s x-directional vibration is very small. The z-directional excitation at the pipe top hardly declines at the buffer (Fig.4).

As shown in Figs.5-7, for the vertical pipe, all force and stress vary at the same trend as those without the account of the heave movement, but fluctuate violently at period of 8 s, the same as the excitation period at the pipe top.

From the analytical results, it can also be found that the z-directional excitation at the pipe top hardly affects the force acting upon the miner, which shows the preferable isolation effect of the flexible riser.

For different amplitudes, analytical results indicate that the amplitude is larger, the force and stress fluctuate more violently. Moreover, the analytical results show that heave movement at the pipe top, with period of 8 s, is not likely to resonate the present pipe.

The steady current is assumed along x direction. Both the ship and miner move along x direction (along the current) at velocity of 0.75 m/s.

In the static state, the excursion of the buffer relative to the ship along x-direction is about 9 m. For the vertical pipe, z-directional force and axial stress are close to those against the current, and the maximum of the x-directional force, z-directional force and axial stress are all located at the top of the vertical pipe. Element 57 still has the maximal bending stress, which is only 2.2 MPa.

When the moving velocity is 1.00 m/s, the configur- ation of the flexible riser is bad, and its horizontal resistance to the miner reaches 18 079 N, which exceeds the operation range of the miner. In view of lower velocity of the water particle relative to the pipe along the current, the velocity can be higher than that against the current, so the velocity is assumed to be 0.75 m/s in the following simulation.

The buffer’s x-directional excursion relative to the ship is about 43 m in steady moving state. During moving, for the vertical pipe, the z-directional force, axial and torsional stresses are almost unchanged. Fig.8 shows the bending stress distribution on the vertical pipe in steady state. Compared with those against the current, the bending stress is reduced on the whole, and element 57 still has the maximal bending stress. The maximal x-directional force is maintained at the pipe top, which is much less than that against the current, as shown in Fig.9. Moreover, the horizontal resistance to the miner by the flexible riser is reduced significantly. The moving velocity may be slightly higher than 0.75 m/s.

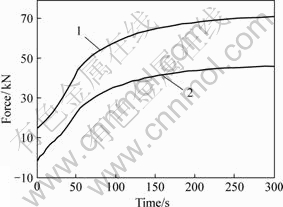
Fig.9 x-direction force at pipe top

1—Against current; 2—Along current

5 Physical experiment

Presently, it is impossible to experiment on deep ocean mining system, so an experiment of physical model similar to sea trial system was developed to verify this modeling method. In the physical model, a stainless pipe, a rubber pipe and a heavy block were used to simulate the vertical pipe, the flexible riser and the buffer in deep ocean mining system. The experiment was operated in a towing tank, and the experiment model was installed on a trailer, whose movement simulated the movement of water. When the trailer moved under several boundary conditions, the calculation results about the configuration and stress of the pipe were in good accordance with the experiment ones.

1) In the present situations, the maximum of z-directional force and axial stress are all maintained at the top of the vertical pipe, and almost keep unchanged. The element next to the pump has the maximal bending stress. On the vertical pipe, the axial stress is dominant. All of these stresses are much less than the allowable value of the vertical pipe and joint.

2) The heave motion at the pipe top leads to violent fluctuation of the force and stress on the vertical pipe, but period of 8 s is not likely to resonate the present pipe.

3) Against the current, it is suggested that 0.50 m/s should be the moving velocity of the ship and miner, while along the current, the moving velocity can be slightly higher than 0.75 m/s.

References

[1] LING Sheng, XIAO Lin-jing, SHEN Yan-hua, et al. A study of the factors influencing the kinematic condition and dynamic characteristics of deep seabed mining systems[J]. Engineering Science, 2002, 4(3): 78-83.(in Chinese)

[2] LIU Shao-jun, WANG Gang, LI Li, et al. Virtual reality research of ocean poly-metallic nodule mining based on COMRA’s mining system[C]// Proceedings of the 5th Ocean Mining Symposium. Tsukuba: ISOPE, 2003: 104-111.

[3] CHUNG J S, WHITNEY A K, LODEN W A. Nonlinear transient motion of deep ocean mining pipe[J]. ASME Journal of Energy Resources Technology, 1981, 103(1): 2-10.

[4] FELIPPA C A, CHUNG J S. Nonlinear static analysis of deep ocean mining pipe-part I: Modeling and formulation[J]. ASME Journal of Energy Resources Technology, 1981, 103(1): 11-15.

[5] CHUNG J S, FELIPPA C A. Nonlinear static analysis of deep ocean mining pipe-part II: numerical studies[J]. ASME Journal of Energy Resources Technology, 1981, 103(1): 16-25.

[6] CHUNG J S, CHENG B R, HUTTELMAIER H P. Three-dimensional coupled responses of a vertical deep-ocean pipe: part I. Excitation at pipe ends and external torsion[J]. Int J Offshore & Polar Eng, ISOPE, 1994, 4(4): 320-330.

[7] CHUNG J S, CHENG B R, HUTTELMAIER H P. Three- dimensional coupled responses of a vertical deep-ocean pipe: part II. excitation at pipe top and external torsion[J]. Int J Offshore & Polar Eng, ISOPE, 1994, 4(4): 331-339.

[8] XIAO Lin-jing, ZENG Qing-liang, ZHANG Wen-ming. Analysis of nonlinear offsetting characteristics on deep ocean mining[J]. Chinese Journal of Mechanical Engineer, 2002, 38(8): 94-99.(in Chinese)

[9] GUO Xiao-gang. Nonlinear dynamic modeling of the fluid-solid- coupled flexible pipe systems for deep sea mining[J]. Engineering Mechanics, 2000, 17(3): 93-104.(in Chinese)

[10] JIAN Qu, HE Yong-sen, WANG Ming-he, et al. Numerical study of dynamic behavior of flexible pipes in deep sea mining[J]. Ocean Engineering, 2001, 19(2): 59-64.(in Chinese)

[11] LI Yan, LIU Shao-jun. Three-dimensional DEM model for deep- Ocean mining pipe system[C]// Proceedings of the 6th Ocean Mining Symposium. Changsha: ISOPE, 2005: 88-93.

[12] HONG S, KIM H W, CHOI J S. A new method using Euler parameters for 3D nonlinear analysis of marine risers/pipelines[C]// Proceedings of the 5th Ocean Mining Symposium. Tsukuba: ISOPE, 2003: 83-90.

[13] ZHU Ke-qiang, LI Wei-yang. Dynamic stability of riser pipeline under the excitation of ocean waves and currents[J]. Journal of East China Ship Building Institute, 1997,11(1): 1-8.(in Chinese)

[14] XU Hai-liang, HE Qing-hua. Analysis on the resistance to motion in the ocean mining transportation system[J]. Mining and Metallurgical Engineer, 2004, 24(5): 9-15.(in Chinese)

[15] TANG Wei, FENG Ya-li, FENG Fu-zhang, et al. Analysis and calculation of the horizontal hydrodynamic force of lifting pipe in 5000 meters′mining system[J]. Metallurgical Equipment, 2005, 153 (3): 5-9.(in Chinese)

[16] YI Qi-le, SHENG Qing-wu, YANG Xian-cheng. Experimental study on fluid dynamic coefficients of circular cylinders with small tubes in oscillating flow[J]. Ship Building of China, 2001, 42(2): 19-25.(in Chinese)

_______________________

Foundation item: Project (DY105-03-02-02) supported by the Deep-Ocean Technology Development Item of China

Received date: 2006-11-24; Accepted date: 2007-01-27

Corresponding author: YU Hong-yun, Doctoral candidate; Tel: +86-731-8830245; E-mail: yhyzlz @163.com

(Edited by YANG Hua)