
ARTICLE
J. Cent. South Univ. (2019) 26: 1260-1270
DOI: https://doi.org/10.1007/s11771-019-4085-8
Features of Darcy-Forchheimer flow of carbon nanofluid in frame of chemical species with numerical significance
Tasawar HAYAT1, 2, Khursheed MUHAMMAD1, Ahmed ALSAEDI3, Muhammas FAROOQ2
1. Department of Mathematics, Quaid-I-Azam University, Islamabad 44000, Pakistan;
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Riphah International University, Islamabad 44000, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract:
Present work reports chemically reacting Darcy-Forchheimer flow of nanotubes. Water is utilized as base liquid while carbon nanotubes are considered nanomaterial. An exponential stretchable curved surface flow is originated. Heat source is present. Xue relation of nanoliquid is employed to explore the feature of CNTs (single and multi-wall). Transformation technique is adopted in order to achieve non-linear ordinary differential systems. The governing systems are solved numerically. Effects of involved parameters on flow, temperature, concentration, heat transfer rate (Nusselt number) with addition of skin friction coefficient are illustrated graphically. Decay in velocity is noted with an increment in Forchheimer number and porosity parameter while opposite impact is seen for temperature. Moreover, role of MWCNTs is prominent when compared with SWCNTs.
Key words:
Cite this article as:
Tasawar HAYAT, Khursheed MUHAMMAD, Ahmed ALSAEDI, Muhammas FAROOQ. Features of Darcy-Forchheimer flow of carbon nanofluid in frame of chemical species with numerical significance [J]. Journal of Central South University, 2019, 26(5): 1260–1270.
DOI:https://dx.doi.org/https://doi.org/10.1007/s11771-019-4085-81 Introduction
Recently advancement in thermal engineering and industrial processing reports a direct impact to have more productive and conservative heat transfer equipments. In order to achieve such goal many investigations have been made by scientists and engineers. They found that the main factor responsible for advanced rate of heat transfer is the thermal conductance of liquids. Also they analyzed that solid particles have better performance in terms of thermal conductance than liquid particles. By adding these solid particles into the liquid, the thermal conductance can be improved. Such particles are known as nanoparticles. Basically liquids which are utilized as cooling agents for cooling purposes have lower thermal conductance. Water, kerosene oil, gasoline oil, ethylene glycol etc may be mentioned here. In order to enhance thermal conductance of such liquids by adding nano sized particle, the first step was taken by CHOI [1]. Such mixture of small (nano) sized particles and base liquid is referred to as nanofluid. Nano materials are of various shapes like spherical, blades, bricks and cylindrical etc. Thermal conductance of base liquid is highly dependent of the shape of nano sized particles. Tube-shaped nano sized particles (cylindrical shaped nano paritcles) show better performance in terms of improving thermal conductance of base liquid [2]. Nanoparticles are made of carbon, silver, gold, titanium etc. Nano materials of carbon include two types, namely single-wall and multi-wall CNTs. There are extensive applications of CNTs like in preparation of bullet proof jackets, table tennis rackets, semiconductors, batteries, solar storages, solar panels, water purification plants and many more [3]. Time-independent squeezed flow of nanoliquid was explored by HAYAT et al [4]. Heat transfer in nanofluid flow using single and multi-wall phase model was investigated by TURKYILMAZOGLU [5]. Chemically reacting nanofluid flow with Newtonian heating was studied by HAYAT et al [6]. SHIEKHOLESLAMI et al [7] analyzed nanofluid flow with natural convection and magnetic field effects. Melting effect in nanomaterial flow by a variable thickened surface was examined HAYAT et al [8]. SOLTANI et al [9] performed an experimental study about nanofluid applications and a hybrid photovoltaic/thermoelectric system. Chemically reactive nanomaterial flow by a variable thickened sheet is deliberated by HAYAT et al [10]. HAYAT et al [11] explored radiative and chemically reactive flow of nanomaterial with melting heat. Entropy generation in non-linear radiative flow of nanofluid is presented by KHAN et al [12]. Melting effect in nanomaterial flow with chemical reactions was considered by HAYAT et al [13]. Chemical reactions in viscous dissipative flow with magnetic effect were presented by KHAN et al [14]. Further some related study of nanomaterial can be seen in Refs. [15–28].
Due to widespread applications the flow by stretching surface has been extensively discussed in literature. In manufacturing processes stretchable surface has vital impact on the finished produced materials. Such sheet has vast range of applications in spinning of fibers, production of paper, rubber sheets, blowing of glass, flow generated in hot rolling, extrusion of polymer sheets and many more. For such processing, the scientists and engineers considered various stretching velocities like exponential, linear and non-linear. Flow over a stretchable surface was initiated by CRANE [29]. Flow of a non-Newtonian fluid with non-Fourier heat flux by a stretchable surface is investigated by HAYAT et al [30]. SHIEKHOLESLAMI et al [31] explored heat transport in flow of nanofluid with porous medium. Three-dimensional squeezed Jeffrey fluid flow in a rotating frame was investigated by HAYAT et al [32]. Viscous fluid flow over a curved surface is analyzed by SAJID et al [33]. Viscous fluid flow over a precurved stretched sheet was deliberated by HAYAT et al [34, 35]. Time-independent flow by a curved stretchable sheet with magnetic field effect was studied by NAVEED et al [36]. Nanomaterial flow by a curved stretched sheet was explored by HAYAT et al [37]. OKETCHI et al [38] considered viscous fluid flow by an exponential curved stretchable surface.
Chemical reactions are of two types: 1) homogeneous reaction, 2) heterogeneous reaction. In chemical reacting processing both the chemical reactions have vital role such as in polymers production, ceramics assembling, combustion, catalysis, food processing, handling crop harms by means of solidification and many more. In boundary layer flow isothermal chemical reaction was studied by MERKIN [39]. KHAN et al [40] analyzed chemical reactions in Darcy-Forchheimer flow. Melting effect in MHD chemically reactive flow by a stretchable surface is presented by HAYAT et al [41]. IMTIAZ et al [42] studied MHD chemically flow by a curved stretchable sheet. Chemically reactive three-dimensional flow along with double diffusion was investigated by HAYAT et al [43]. IMTIAZ et al [44] explored chemically reactive flow of ferrofluid over a curved surface. Chemical reactions in Sisko-fluid were elaborated by HAYAT et al [45]. QAYYUM et al [46] analyzed flow of silver and copper water based nano materials with chemical reactions and non-linear thermal radiations. Chemically reactive nanofluid flow with magnetic effect was presented by HAYAT et al [47]. Joule heating in chemically reactive flow with Joule heating effect was considered by KHAN et al [14].
Studying the features of fluids subjected to high rate of heating and cooling, the engineers and scientists had only paid much concentration to the dispersion of nano materials of Al2O3, Ag in the base liquids. In this paper our main aim is to develop analysis and modeling of high rate of heating or cooling by dispersing single and multi-wall CNTs in the base liquid known as water. Heat source and Darcy-Forchheimer porous medium are considered in flow field. Fluid flow and heat transport characteristics are explored in presence of and heat source. Exponentially curved stretchable surface is considered. The governing expressions for flow field are solved by bvp4c (a MATLAB tool). Flow, rate of heat transfer, temperature with addition of skin friction coefficient under the impact of influential parameters are sketched graphically.
2 Mathematical modeling
We assume steady incompressible carbon nanomaterial flow by an exponentially stretchable surface. Flow behavior is analyzed via Darcy- Forchheimer porous medium. Homogeneous- heterogeneuos reactions are taken into account. We have adopted curvilinear coordinates such that s-axis is taken along the exponential curved stretched surface while r-axis is perpendicular to it (see Figure 1). For cubic catalysis the homogeneous reaction is defined as [13]:
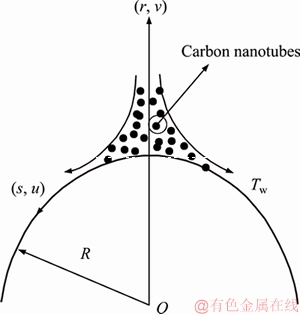
Figure 1 Geometry for flow field
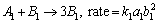 (1)
(1)
 (2)
(2)
Furthermore, the reaction equations guarantee that rate of reaction is zero in the external flow as well as at outer edge of the boundary layer. After ignoring thermal radiation and viscous dissipation, the flow field under mentioned assumptions becomes [27–32]:
 (3)
(3)
 (4)
(4)
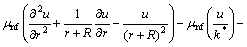
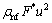 (5)
(5)
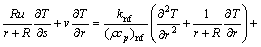
 (6)
(6)
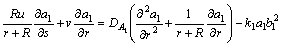 (7)
(7)
 (8)
(8)
with associated boundary conditions
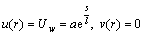
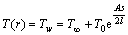 (9)
(9)
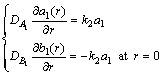 (10)
(10)
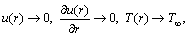
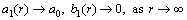 (11)
(11)
According to Xue relations for carbon nanotubes we have [48]:
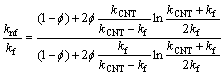 ,
,
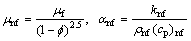 ,
,
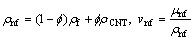 (12)
(12)
Implemented transformations are [38]
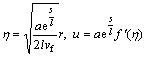 ,
,
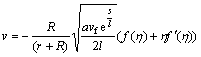 ,
,
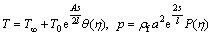 ,
,
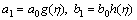 (13)
(13)
Continuity Eq. (3) is verified while Eqs. (4)–(8) give
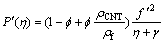 (14)
(14)
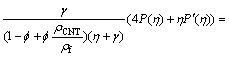
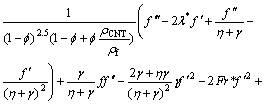
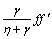 (15)
(15)
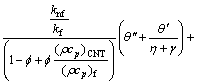
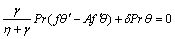 (16)
(16)
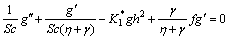 (17)
(17)
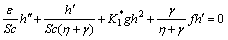 (18)
(18)
The subjected boundary conditions are

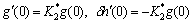 (19)
(19)

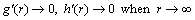 (20)
(20)
Assuming that both and
and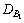 equal i.e., ε=1, we have
equal i.e., ε=1, we have
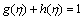 (21)
(21)
Equations (15) and (16) give
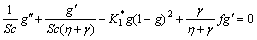 (22)
(22)
with
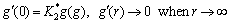 (23)
(23)
The involved physical variables are defined by
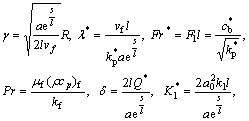
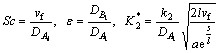
After the elimination of P from Eqs. (15) and (16), we get
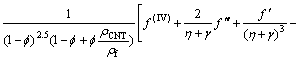
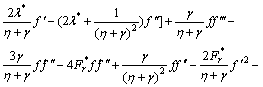
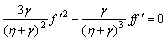 (24)
(24)
Dimensional skin friction and local Nusselt number for the considered flow field are
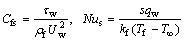 (25)
(25)
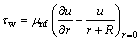 ,
,
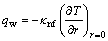 (26)
(26)
while in dimensionless form:
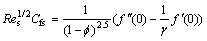 ,
,
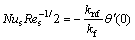 (27)
(27)
where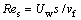 presents the local Reynolds number.
presents the local Reynolds number.
3 Solution via bvp4c
We have solved nonlinear ODEs numerically with the help of bvp4c technique. This method solves first order ODEs. That is why we have converted these higher order ODEs along with boundary conditions into first order ODEs. Thus we adopted procedure as [49, 50]:
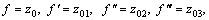
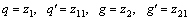
where z′0=z01, z′01=z02, z′02=z03, z′1=z11, z′2=z21, 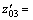

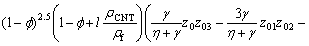
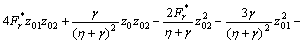
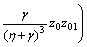 ,
,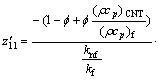
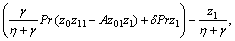
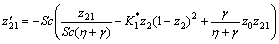
while the boundary conditions are z0(0)=0, z01(0)=1, z11(0)=1, z21(0)=K*2z2(0), z02→0, z01→0, z1→0, z21→0, as η→∞.
The above system of first order ODE’s is further solved by finite difference scheme which follows the three-stage Lobatto IIIa formula in MATLAB software.
4 Description
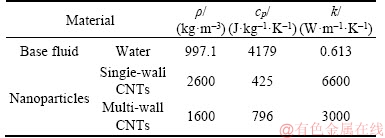
This section reports the variations of involved variables on temperature, flow, concentration, local Nusselt number and skin friction coefficient.Figure 1 represents the schematic diagram for the flow field. Figures 2–6 present the variation in velocity via f, γ, Fr* and λ* respectively. It has been deliberated that velocity enhances through increment in f, while γ decrement has been noticed for higher Fr* and λ*. It is due to the fact that increment in γ leads to enlargement in radius of curved surface and thus a large number of particles are stuck with the surface due to the fact that increment in velocity is observed. Similarly, larger Fr* corresponds to generation of higher drag forces (resistive forces) and as a result of these forces the fluid velocity decreases. Increment in λ* corresponds to the presence of more porous space due to the fact that more resistance is experienced by the fluid which degrades fluid velocity. Temperature of fluid via f, Fr*, λ, δ and A are designed in Figures 7–10, respectively. Enlargement in f, Fr*, λ*and δ leads to increment in fluid temperature. Furthermore, multi-wall CNTs dominates over single-wall CNTs. Higher f corresponds to larger thermal conductivity of base liquid. Temperature of fluid particles enhances gradually, which results an increment in velocity of fluid. Similarly, Fr* produces more resistive force between the particles of fluid and is responsible for the enhancement of temperature. Increment in porous space occurs with increase in λ*, which results in more resistance to the fluid flow. Hence decay in temperature occurs. Increment in δ leads to increase in temperature. Physically δ>1 demonstrates that Tw>T∞. i.e., more heat transfer occurs from curved surface towards fluid and consequently there is an enhancement of fluid temperature. Multi-wall CNTs are dominant over single-wall CNTs. Figures 11–13 are displayed for the variation in concentration due to higher K*1, K*2 and Sc. It is noticed that concentration raises while the corresponding penetration depth declines for larger Sc. Sc is ratio of mentum diffusivity to mass diffusivity. Thus higher Sc leads to decay in mass diffusion, as a result enhancement of concentration occurs. Figure 14 is drawn for variations in skin friction coefficient via f, γ, Fr* and λ*. Skin friction is lager for higher f, Fr* and λ* while opposite behavour is examined for larger γ. Figure 15 is labelled for the variation of local Nusselt number via f, δ, A and γ. Reduction in Nusselt number is seen for higher f while opposite trend has been observed for larger γ, Fr* and λ*. Multi-wall CNTs show dominating features when compared with single-wall CNTs. Thermophysical features of the base liquids (water) and nanomaterials are presented in Table 2.
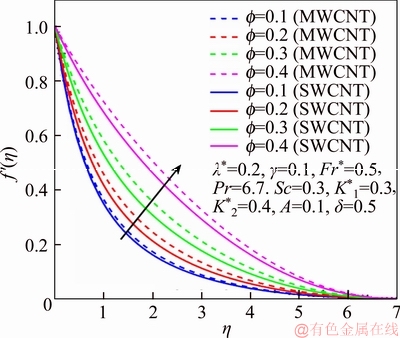
Figure 2 f ′ via f
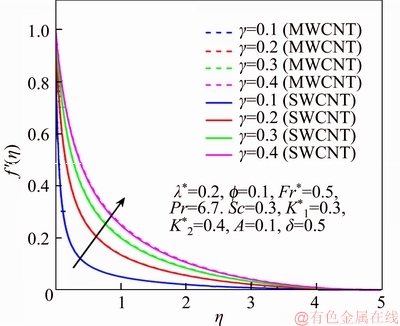
Figure 3 f ′ via γ
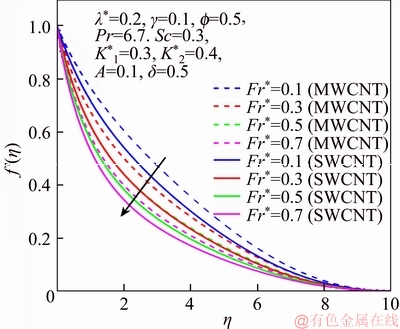
Figure 4 f ′ via Fr
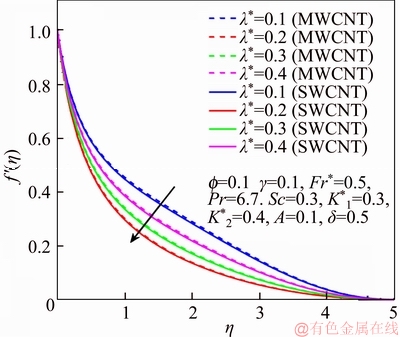
Figure 5 f ′ via λ*
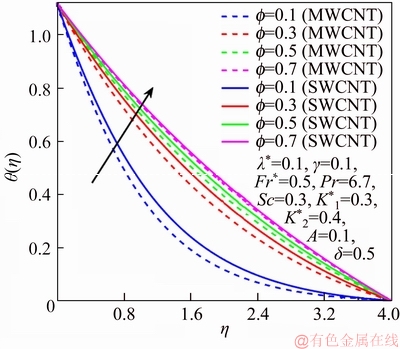
Figure 6 θ via f
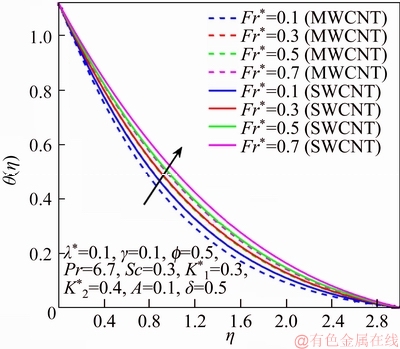
Figure 7 θ via Fr*

Figure 8 θ via λ*
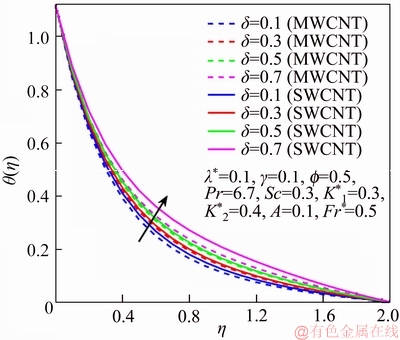
Figure 9 θ via δ
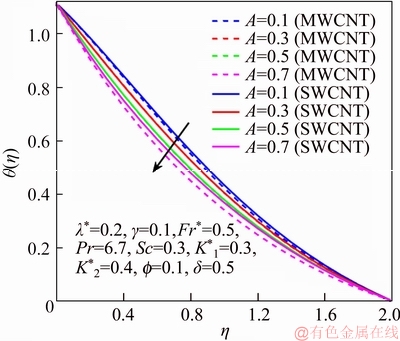
Figure 10 θ via A
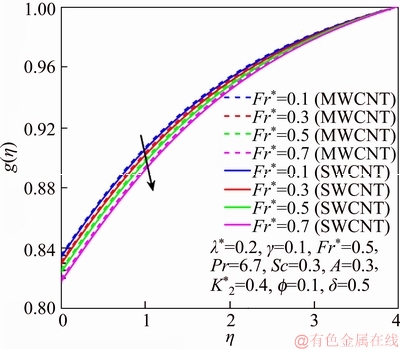
Figure 11 g via Fr*
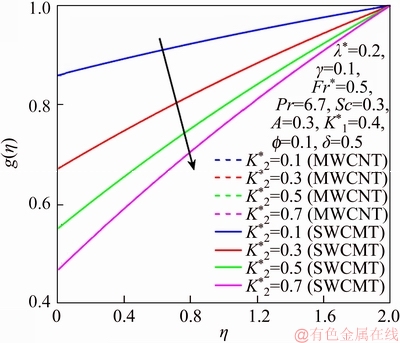
Figure 12 g via K*2
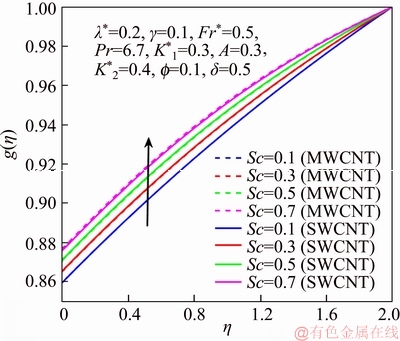
Figure 13 g via Sc
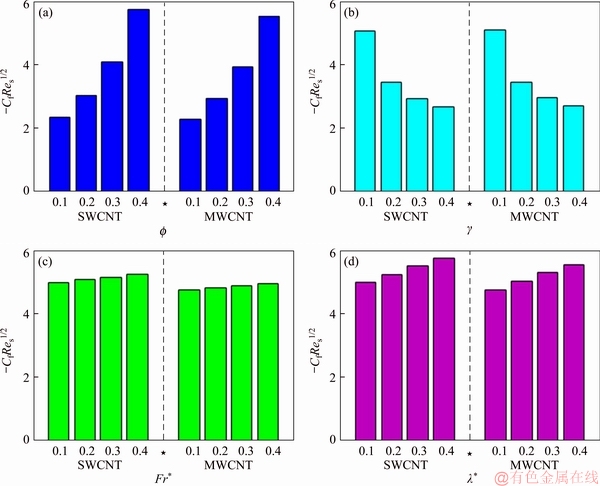
Figure 14 Cf variations vs f (a), γ (b), Fr* (c) and λ* (d)
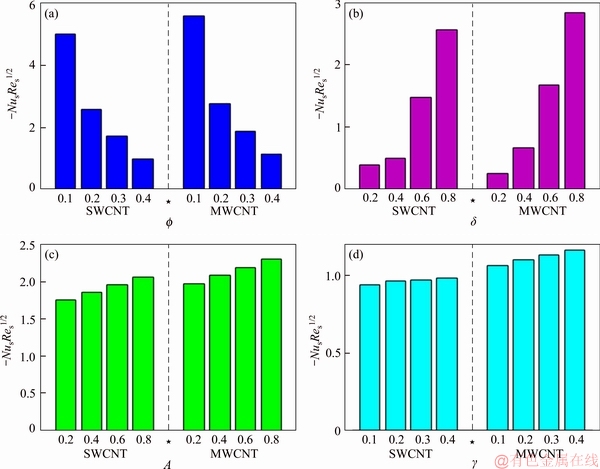
Figure 15 Nus variations vs f (a), δ (b), A (c) and γ (d)
Table 2 Physical characteristics of CNTs and water [11]
5 Conclusions
1) An intensification in velocity occurs for higher values of f and γ while reduction in velocity is observed for larger Fr* and λ*.
2) Temperature of fluid enhances with enlargement in f , Fr*, λ*, δ and A.
3) Larger K*1 reduces concentration while it enlarges with an increment in λ*, K*2 and Sc.
4) Increment in skin friction occurs via f , Fr* and λ* where it reduces for larger γ.
5) Heat transfer rate is higher for δ, A and γ while it reduces for larger f.
6) Impacts of multi-wall CNTs on local Nusselt number as well as skin friction coefficient are more than those of single-wall CNTs.
7) Cooling process of can be regulated by higher A and γ.
8) Flow can be controlled via larger Fr* and λ*.
9) In future one may study CNTs based flow with entropy production through viscous or non-Newtonian fluids.
10) Cavity flow in this direction can also be examined.
Nomenclature
u, v
Components of velocity
μf
Dynamic viscosity of baseliquid
vf
Kinematic viscosity of base liquid
Uw
Surface stretching velocity
a
Positive constant
fnf
Thermal conductivity of nanoliquid
(cp)f
Specific heat of base liquid
k*p
Porous medium permeability
Tf
Temperature of hot fluid
Fr*
Forchheimer number
h*
Heat transfer coefficient
θ
Dimensionless temperature
(cp)nf
Specific heat of nanofluid
η
Dimensionless variable
Pr
Prandtl number
CNTs
Carbon nanotubes
k1, k2
Rate constants
F*1
Homogeneous reaction parameter
F*2
Heterogeneous reaction parameter
m
Behavior index
Res
Local Reynolds number
τw
Wall shear stress
A1, B1
Chemical species
Sc
Schmidt number
s, r
Curvilinear coordinates
ρf
Base fluid density
f1
Porosity of porous medium
c*b
Drag coefficient
vnf
Kinematic viscosity
Of nanoliquid
kf
Base liquid thermal conductivity
αf
Thermal diffusivity of base liquid
p
Pressure
T∞
Temperature of the ambient fluid
P
Dimensionless pressure
F*
Non-uniform inertia coefficient of porous medium
f
Nanoparticle volume fraction
αnf
Thermal diffusivity of nanofluid
Q*
Heat source coefficient
kCNT
Thermal conductivity of CNTs
γ
Curvature parameter
DA1, DB1
Diffusion coefficient of species A1 B1
g
Concentration
ε
Ratio of diffusion coefficients
f ′
Dimensionless velocity
δ
Heat source parameter dimensionless
λ*
Porosity parameter
a1, b1
Concentration of species A1 and B1
References
[1] CHOI S U S. Enhancing thermal conductivity of fluids with nanoparticles [C]// SIGINER D A, WANG H P. Development and Application of non-Newtonian Flows. New York: ASME, FED-vol. 231/MD 66, 1995: 99–105.
[2] ELIAS M M, MIQDAD M, MAHABUBUL I M, SAIDUR R, KAMALISAVESTANI M, SOHEL M R, HAPBASLI A, RAHIM N A, AMALINA M A. Effect of nanoparticle shape on the heat transfer and thermodynamic performance of a shell and tube heat exchanger [J]. International Communications in Heat and Mass Transfer, 2013, 44: 93–99.
[3] VOLDER M F L D, TAWFIC S H, BAUGHMAN R H, HART A J. Carbon nanotubes: Present and future commercial applications [J]. Science, 2013, 339: 535–539.
[4] HAYAT T, MUHAMMAD K, FAROOQ M, ALSAEDI A. Unsteady squeezing flow of carbon nanotubes with convective boundary conditions [J]. PLOS One, 2016, 11: 0152923.
[5] TURKYILMAZOGLU M. Analytical solutions of single and multi-phase models for the condensation of nanofluid film flow and heat transfer [J]. European Journal of Mechanics, B/Fluids, 2015, 53: 272–277.
[6] HAYAT T, FAROOQ M, ALSAEDI A. Homogenous- heterogenous reactions in the stagnation point ow of carbon nanotubes with Newtonian heating [J]. AIP Advances, 2015, 5: 027130.
[7] SHIEKHOLESLAMI M, ELLAHI R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid [J]. International Journal of Heat and Mass Transfer, 2015, 89: 799–808.
[8] HAYAT T, MUHAMMAD K, FAROOQ M, ALSAEDI A. Melting heat transfer in stagnation point flow of carbon nanotubes towards variable thickness surface [J]. AIP Advances, 2016, 6: 015214.
[9] SOLTANI S, KASAEIAN A, SARRAFHA H, WEN D. An experimental investigation of a hybrid photovoltaic/ thermoelectric system with nanofluid application [J]. Solar Energy, 2017, 115: 1033–1043.
[10] HAYAT T, AHMED S, MUHAMMAD T, ALSAEDI A. Modern aspects of homogeneous-heterogeneous reactions and variable thickness in nanofluids through carbon nanotubes [J]. Physica E: Low-dimensional Systems and Nanostructures, 2017, 94: 70–77.
[11] HAYAT T, MUHAMMAD K, MUHAMMAD T, ALSAEDI A. Melting heat in radiative flow of carbon nanotubes with homogeneous-heterogeneous Reactions [J]. Communicatins in Theoritical Physics, 2018, 69: 441–448.
[12] KHAN M I, ULLAH S, HAYAT T, KHAN M I, ALSAEDI A. Entropy generation minimization (EGM) for convection nanomaterial flow with nonlinear radiative heat flux [J]. Journal of Molecular Liquids, 260, 2018: 279–291.
[13] HAYAT T, MUHAMMAD K, ALSAEDI A, ASGHAR S. Numerical study for melting heat transfer and homogeneous- heterogeneous reactions in flow involving carbon nanotubes [J]. Results in Physics, 2018, 8: 415–421.
[14] KHAN M I, HAYAT T, KHAN M I, ALSAEDI A. A modified homogeneous-heterogeneous reaction for MHD stagnation flow with viscous dissipation and Joule heating [J]. International Journal of Heat and Mass Transfer, 2017, 113: 310–317.
[15] SHEIKHOLESLAMI M, HAYAT T, ALSAEDI A, ABELMAN S. Numerical analysis of EHD nanofluid force convective heat transfer considering electric field dependent viscosity [J]. International Journal of Heat and Mass Transfer, Part B, 2017, 108: 2558–2565.
[16] SELIMEFENDIGIL F,  ZTOP H F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity [J]. International Journal of Heat and Mass Transfer, 2019, 129: 265–277.
ZTOP H F. Corrugated conductive partition effects on MHD free convection of CNT-water nanofluid in a cavity [J]. International Journal of Heat and Mass Transfer, 2019, 129: 265–277.
[17] SHEIKHOLESLAMI M, JAFARYAR M, LI Z. Second law analysis for nanofluid turbulent flow inside a circular duct in presence of twisted tape turbulators [J]. Journal of Molecular Liquids, 2018, 263: 489–500.
[18] SELIMEFENDIGIL F,  ZTOP H F. Numerical analysis and ANFIS modeling for mixed convection of CNT-water nanofluid filled branching channel with an annulus and a rotating inner surface at the junction [J]. International Journal of Heat and Mass Transfer, 2018, 127: 583–599.
ZTOP H F. Numerical analysis and ANFIS modeling for mixed convection of CNT-water nanofluid filled branching channel with an annulus and a rotating inner surface at the junction [J]. International Journal of Heat and Mass Transfer, 2018, 127: 583–599.
[19] SHEIKHOLESLAMI M, HAYAT T, ALSAEDI A. MHD free convection of Al2O3–water nanofluid considering thermal radiation: A numerical study [J]. International Journal of Heat and Mass Transfer, 2016, 96: 513–524.
[20] SELIMEFENDIGIL F,  ZTOP H F. Forced convection and thermal predictions of pulsating nanofluid flow over a backward facing step with a corrugated bottom wall [J]. International Journal of Heat and Mass Transfer, 2017, 110: 231–247.
ZTOP H F. Forced convection and thermal predictions of pulsating nanofluid flow over a backward facing step with a corrugated bottom wall [J]. International Journal of Heat and Mass Transfer, 2017, 110: 231–247.
[21] SHEIKHOLESLAMI M, HAYAT T, ALSAEDI A. Numerical simulation of nanofluid forced convection heat transfer improvement in existence of magnetic field using lattice Boltzmann method [J]. International Journal of Heat and Mass Transfer, 2017, 108: 1870–1883.
[22] MAJID S, MOHAMMAD J. Optimal selection of annulus radius ratio to enhance heat transfer with minimum entropy generation in developing laminar forced convection of water-Al2O3 nanofluid flow [J]. Journal of Central South University, 2017, 24: 1850–1865.
[23] SHEIKHOLESLAMI M, HAYAT T, ALSAEDI A. Numerical study for external magnetic source influence on water based nanofluid convective heat transfer [J]. International Journal of Heat and Mass Transfer, 2017, 106: 745–755.
[24] SARI M R, KEZZAR M, ADJABI R. Heat transfer of copper/water nanofluid flow through converging-diverging channel [J]. Journal of Central South University, 2016, 23: 484–496.
[25] SIAVASHI M, GHASEMI K, YOUSOFV R, DERAKHSHAN S. Computational analysis of SWCNH nanofluid-based direct absorption solar collector with a metal sheet [J]. Solar Energy, 2018, 170: 252–262.
[26] SIAVASHI M, RASAM H, IZADI A. Similarity solution of air and nanofluid impingement cooling of a cylindrical porous heat sink [J]. J Therm Anal Calorim, 2018, 135: 1399–1415. DOI: doi.org/10.1007/s10973-018-7540-0.
[27] HAYAT T, MUHAMMAD K, ULLAH I, ALSAEDI A, ASGHAR S. Rotating squeezed flow with carbon nanotubes and melting heat [J]. Physysica Scripta, 2018. DOI: doi.org/10.1088/1402-4896/aaef66.
[28] MAHIAN O, KOLSI L, AMANI M, ESTELL P, AHMADI G, KLEINSTREUER C, MARSHALL J S, TAYLOR R A, ABU-NADA E, RASHIDI S, NIAZMAND H, WONGWISES S, HAYAT T, KASAEIAN A, POP I. Recent advances in modeling and simulation of nanofluid flows-Part II: Applications [J]. Physics Reports, 2018, 791: 1–59. DOI: doi.org/10.1016/j.physrep.2018.11.003.
P, AHMADI G, KLEINSTREUER C, MARSHALL J S, TAYLOR R A, ABU-NADA E, RASHIDI S, NIAZMAND H, WONGWISES S, HAYAT T, KASAEIAN A, POP I. Recent advances in modeling and simulation of nanofluid flows-Part II: Applications [J]. Physics Reports, 2018, 791: 1–59. DOI: doi.org/10.1016/j.physrep.2018.11.003.
[29] CRANE L J. Flow past a stretching plate [J]. Zeitschrift fur Angewandte Mathematik und Physik, 1970, 21: 645–641.
[30] HAYAT T, MUHAMMAD T ALSAEDI A. Impact of Cattaneo-Christov heat flux in three-dimensional flow of second grade fluid over a stretching surface [J]. Chinese Journal of Physics, 2017, 55: 1242–1251.
[31] SHIEKHOLESLAMI M, ELLAHI R, ASHORYNEJAD H R, DOMAIRRY G, HAYAT T. Effects of heat transfer in flow of nanofluids over a permeable stretching wall in a porous medium [J]. J Comput Theor Nanos, 2014, 11: 486–496.
[32] HAYAT T, MUHAMMAD K, FAROOQ M, ALSAEDI A. Squeezed flow subject to Cattaneo-Christov heat flux and rotating frame [J]. Journal of Molecular Liquids, 2016, 220: 216–222.
[33] SAJID M, ALI N, JAVED T, ABBAS Z. Stretching a curved surface in a viscous fluid [J]. Chin Phys Lett, 2010, 27: 024703.
[34] HAYAT T, SAIF R S, ELLAHI R, MUHAMMAD T, AHMAD B. Numerical study of boundary-layer flow due to a nonlinear curved stretching sheet with convective heat and mass conditions [J]. Results in Physics, 2017, 7: 2601–2606.
[35] HAYAT T, HAIDER F, MUHAMMAD T, ALSAEDI A. Darcy-Forchheimer flow due to a curved stretching surface with Cattaneo-Christov double diffusion: A numerical study [J]. Results in Physics, 2017, 7: 2663–2670.
[36] NAVEED M, ABBAS Z, SAJID M. Hydromagnetic flow over an unsteady curved stretching surface [J]. Engineering Science and Technology, an International Journal, 2016, 19: 841–845.
[37] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. Numerical study for nanofluid flow due to a nonlinear curved stretching surface with convective heat and mass conditions [J]. Results in Physics, 2017, 7: 3100–3106.
[38] OKECHI N F, JALILA M, AND ASGHAR S. Flow of viscous fluid along an exponentially stretching curved surface [J]. Results in Physics, 2017, 7: 2851–2854.
[39] MERKIN J H. A model for isothermal homogenous- heterogenous reactions in boundarylayer flow [J]. Math Computer Model, 1996, 24: 125–136.
[40] KHAN M I, HAYAT T, ALSAEDI A. Numerical analysis for Darcy-Forchheimer flow in presence of homogeneous- heterogeneous reactions [J]. Results in Physics, 2017, 7: 2644–2650.
[41] HAYAT T, KHAN, I, ALSAEDI A,
[42] IMTIAZ M, HAYAT T, ALSAEDI A. MHD convective flow of Jeffrey fluid due to a curved stretching surface with homogeneous-heterogeneous reactions [J]. PLOS One, 2016, 9: e0161641.
[43] HAYAT T, AYUB T, MUHAMMAD T, ALSAEDI A. Three-dimensional flow with Cattaneo-Christov double diffusion and homogeneous-heterogeneous reactions [J]. Results in Physics, 2017, 7: 2812–2820.
[44] IMTIAZ M, HAYAT T ALSAEDI A. Convective flow of ferrofluid due to a curved stretching surface with homogeneous-heterogeneous reactions [J]. Powder Technology, 2017, 310: 154–162.
[45] HAYAT T, ULLAH I, ALSAEDI A, AHMAD B. Numerical simulation for homogeneous-heterogeneous reactions in flow of Sisko fluid [J]. J Braz Soc Mech Sci Eng, 2018, 40: 73.
[46] QAYYUM S, KHAN M I, HAYAT T, ALSAEDI A. A framework for nonlinear thermal radiation and homogeneous-heterogeneous reactions flow based on silver-water and copper-water nanoparticles: A numerical model for probable error [J]. Results Phys, 2017, 7: 1907–1914.
[47] HAYAT T, ULLAH I, WAQAS M, ALSAEDI A. Flow of chemically reactive magneto Cross nanoliquid with temperature-dependent conductivity [J]. Appl Nanosci, 2018. DOI: doi.org/10.1007/s13204-018-0813.
[48] XUE Q. Model for thermal conductivity of carbon nanotube based composites [J]. Phys B: Condens Matter, 2005, 368: 302–307.
[49] KHAN M I, QAYYUM S, HAYAT T, WAQAS M, KHAN M I, ALSAEDI A. Entropy generation minimization and binary chemical reaction with Arrhenius activation energy in MHD radiative flow of nanomaterial [J]. Journal of Molecular Liquids, 2018, 259: 274–283.
[50] PRAKASH J, RAMESH K, TRIPATHI D, KUMAR R. Numerical simulation of heat transfer in blood flow altered by electroosmosis through tapered micro-vessels [J]. Microvascular Research, 2018, 118: 162–172.
(Edited by YANG Hua)
中文导读
碳纳米流体的Darcy-Forchheimer流体特征在化学物质框架中的数值意义
摘要:本文对碳纳米管中发生的Darcy-Forchheimer流体化学反应进行了研究。当碳纳米管被认为是纳米材料时,使用水作基液,由于指数拉伸弯曲表面流动的产生而出现热源。采用纳米液体的薛氏关系式研究了碳纳米管(单壁、多壁碳纳米管)的特性。利用变换技术得到非线性常微分方程,对控制系统进行数值求解。用图示说明所涉及的参数在增加表面摩擦系数的情况下,对流动、温度、浓度、热传递速率(Nusselt数)的影响。速度随着Forchheimer数和孔隙度的增大而减慢,但温度则呈相反的趋势。与单壁碳纳米管相比,多壁碳纳米管的作用更显著。
关键词:化学反应;Darcy-Forchheimer流体;指数拉伸曲面;碳纳米材料;数值解
Received date: 2018-10-20; Accepted date: 2019-01-31
Corresponding author: Khursheed MUHAMMAD, PhD; Tel: +92-5190642; E-mail: kmuhammad@math.qau.edu.pk; ORCID: 0000- 0003-1161-4510
Abstract: Present work reports chemically reacting Darcy-Forchheimer flow of nanotubes. Water is utilized as base liquid while carbon nanotubes are considered nanomaterial. An exponential stretchable curved surface flow is originated. Heat source is present. Xue relation of nanoliquid is employed to explore the feature of CNTs (single and multi-wall). Transformation technique is adopted in order to achieve non-linear ordinary differential systems. The governing systems are solved numerically. Effects of involved parameters on flow, temperature, concentration, heat transfer rate (Nusselt number) with addition of skin friction coefficient are illustrated graphically. Decay in velocity is noted with an increment in Forchheimer number and porosity parameter while opposite impact is seen for temperature. Moreover, role of MWCNTs is prominent when compared with SWCNTs.


